某口径火箭发动机温度场特性研究

郁安吉,薛晓春,余永刚

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

装药温度是影响箭炮武器性能的重要因素,药温测量的精度将直接影响火箭弹道解算结果的正确性,进而影响武器性能[1-2]。因此,准确获得火箭发动机内部热环境参数是对其热防护系统进行精细化设计的前提[3]。

通常可采用传热相似法和解算法两种方法进行装药温度的测量。解算法是利用传热学基本原理,通过测量环境温度,对装药温度场进行解算[4];传热相似法是采用缩比模型,通过相似原理和无量纲分析,保证其传热过程的微分方程和单值条件相同[5],可满足各类火箭实时弹道解算的要求。刘庆才等[6]利用解算法对固体推进剂建立了导热模型,使用非接触式试验装置对推进剂的温度场进行了测定,得到的计算结果与实验测点温度值吻合较好。周彦煌等[7]利用全自动间接测量法,通过微机控制的非接触式实时测量装置,设计出的装药温度自动测量系统实现了药温自动实时测量,满足当代作战需要。

目前大口径火箭发动机达到平衡温度所需时间过长,增加了试验的能耗,影响其研制效率,而装药温度场的变化特性是确定该时间的前提[8-9]。因此,科研人员在大口径武器弹药保温方面进行了深入研究[10]。李媛等[11]为研究环境温度对固体火箭发动机药柱温度场的影响,利用有限元传热进行分析。薛青等[12]根据发射药保温的原理,通过仿真与试验相结合的方法,验证发射装药保温过程弹药温度接近环境温度需要的时间远低于现有标准所规定的时间。

针对火箭发动机装药温度场平衡温度所需时间的计算问题,本文采取数值传热学理论与实验相结合的方法,建立了火箭发动机的传热数学模型,针对不同环境温度条件下的某火箭发动机的温度场进行试验测试;通过对比数值计算与实验结果,验证了所建立的多层材料间传热模型的合理性;最后深入分析了火箭发动机各层材料的温度变化特性。

1 装药温度场数值模拟

1.1 数理模型

由于火箭发动机是由金属壳体、绝缘层和推进剂装药等多层材料组成,试验中在装药上选取多个具有代表性的测点,安装完传感器后将实验模型放入保温箱,进行保温测试。因此,为了模拟这种多层材料在高温或者低温环境中的温度场特性,建立如图1所示的物理模型,并取a、b、c三点作为特征点记录其温度变化特性,其中a点位于装药1/3位置,b点位于装药1/2位置,c点位于装药2/3位置。针对该物理模型,提出以下假设:

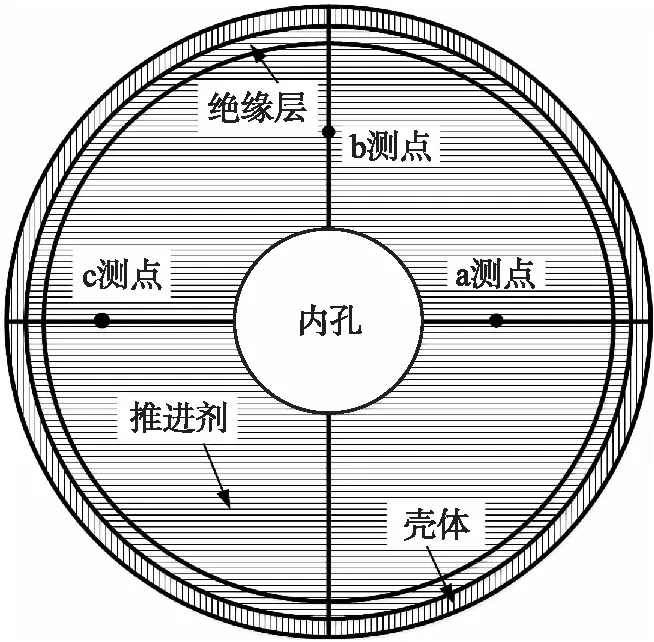
图1 某火箭发动机物理模型Fig.1 Physical model of a rocket engine

①由于发动机温度沿径向变化较大,因此采用一维柱坐标描述这种多层材料间的非稳态传热现象;

②各层材料间无热阻;

③空气的导热系数和比热只是温度的函数;

④发动机各层材料的物性参数为常数。

针对上述假设,建立这种多层材料间的传热模型:

(1)

式中:T为发射药温度;r为发动机截面径向坐标;λi、ρi、ci分别是材料(i=1时为推进剂、i=2时为绝缘层、i=3时为发动机壳体)的导热系数、密度和比热容。

1.2 初始条件及边界条件处理

初始时刻求解区域内各点的温度相同,即初始条件为

T(t,r)|t=0=f(0,r)

(2)

当火箭发动机处在高温或低温环境中时,受外界热源或者冷源的对流传热作用,其内各层材料的温度均会发生变化,并不断接近环境温度。因此,采用第三类边界条件作为发动机内孔内边界条件和发动机壳体外边界条件:

(3)

(4)

式中:Rs、Rn分别为发动机内孔内径和发动机壳体半径;Tws为发射药内边界温度;Twn为发动机壳体外边界温度;Tfs和Tfn分别为内环境和外环境温度。hs和hn分别为发动机内外边界的对流换热系数,通过努塞尔数Nu计算。如下所示:

Nu=C(GrPr)b

(5)

(6)

式中:C,b为实验系数;Pr=0.7;αV为空气体积膨胀系数;g为重力加速度;ΔT为壁面与环境的温差;δ为特征长度;μ为空气动力黏度。

1.3 数值计算方法

采用控制容积法离散传热方程,求解区域离散采用内节点法,将推进剂、绝缘层、壳体和空气层进行网格划分,并在时间间隔[t,t+Δt]内将非稳态导热方程对控制体作积分:

(7)

假定方程非稳态项中温度随时间和空间都是阶梯性变化,扩散项随空间分段线性变化,随时间阶梯性变化,则有:

(8)

式中:下标P,S,N表示求解区域相应网格节点;半径方向相邻两节点间的距离以δr表示,下标s,n表示相应控制容积界面;上标0表示上一时刻的值。离散后方程可写为

(9)

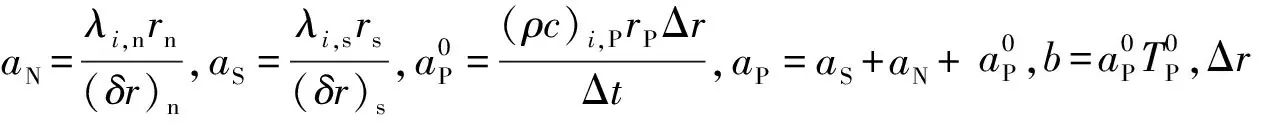
为使方程(9)封闭,采用附加源项法进一步处理边界条件,即考虑所有节点上离散方程系数形式的一致性,对于内外边界而言,将方程的系数aP和b改写如下:

(10)

式中:SC,SP为一般传热控制方程形式中源项作局部线性化处理后的系数。由于装药与环境温度之间传热是无源的,即:SC=0,SP=0,其余参数保持不变,因此改写上述系数不影响离散后传热控制方程的解。

对于求解区域边界上的节点而言,由于采用了附加源项法处理边界条件,其源项部分即SC、SP不为0,因此上述的SC、SP为0仅满足求解区域上的内部节点。但由于添加了SC,ad、SP,ad部分,使得发射装药与环境温度之间的传热关系式离散后的系数在求解区域上对所有节点具有了统一的形式,有利于程序的编制。

根据图2对边界条件进行处理,先对位于边界上的N节点表示的边界条件进行研究。

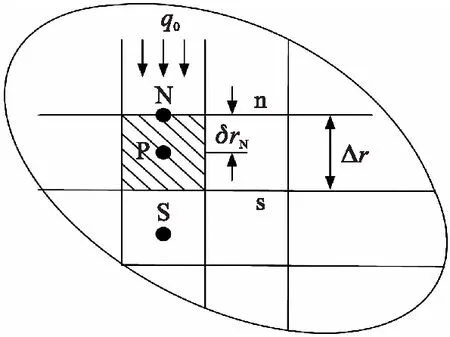
图2 附加源项图示说明Fig.2 Illustration of additional source items

系数aN表示为

(11)

式中:rp为边界点N到P点的距离,λb为边界节点的导热系数。

边界条件可改写为

(aP-aN)TP=aN(TN-TP)+aSTS+b

(12)

利用已知的边界条件把TN消去未知的边界温度,由Fourier定律得:

(13)

得:

(14)

于是,有

(15)

式中:h为表面对流换热系数;SC,ad、SP,ad为附加源项。

1.4 多层材料的参数处理

火箭发动机是由多层材料组成,多层材料间物性均采用调和平均方法进行计算,各层材料(发动机壳体、绝缘层及推进剂)的导热系数、密度和比热容,其物性参数见表1。

表1 材料物性参数Table 1 Physical property parameters of materials

2 结果对比分析

2.1 数值模型的验证

为了验证上述数值模型的合理性,本文对20 ℃环境条件下的初温-40 ℃的某火箭发动机温度变化特性进行了实验研究,温度测点位置按图1所示布置。发动机内部温度的数值计算结果与实验测量变化曲线如图3所示。可知,a,b,c测点处的数值计算与实验最大误差分别为6.72%、7.84%和7.96%,且在整个升温过程中,通过式(16)可得数值计算与实验的温度误差最大为1.423 ℃;

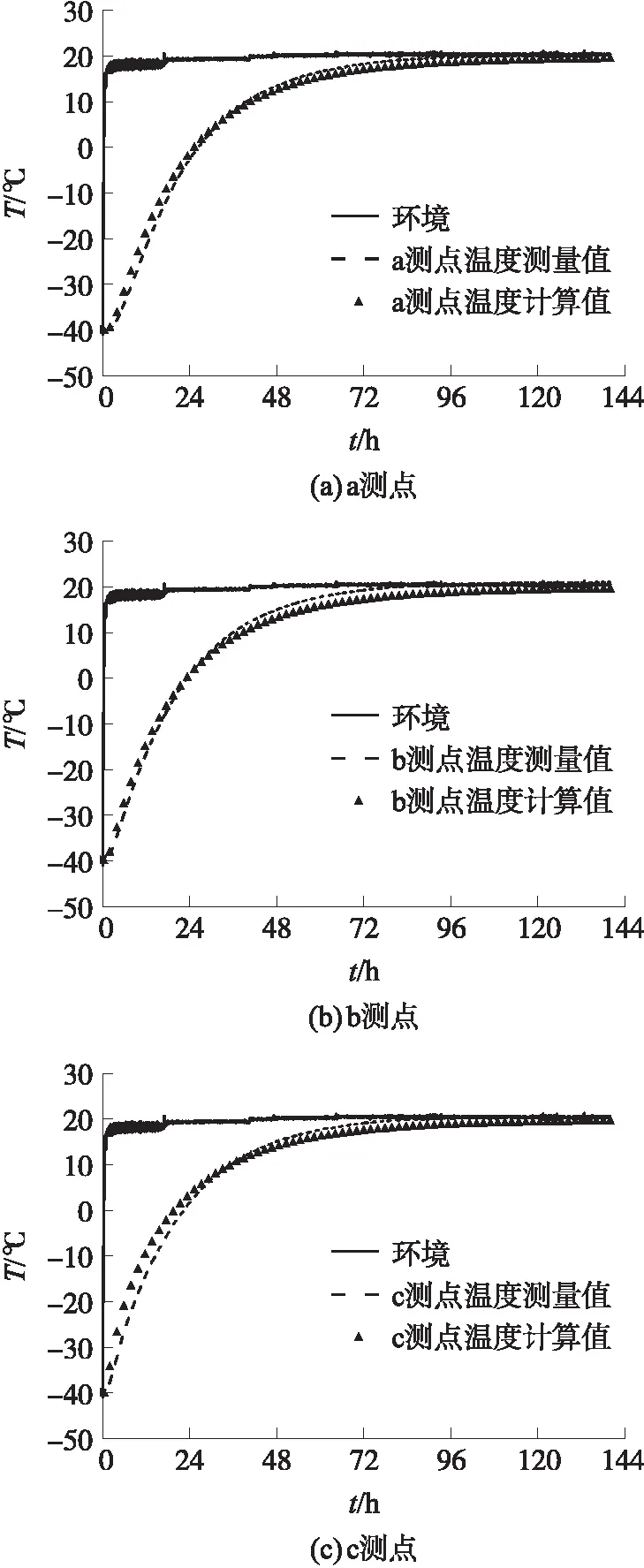
图3 实验与数值计算结果对比图Fig.3 Comparison of experimental data and calculation results

(16)

式中:TE,k为实验测量值,TC,k为理论计算值,n为统计次数。

2.2 发动机温度特性分析

2.2.1 升温过程分析

为了探究升温过程中,发动机初始温度对其温度场的影响,针对环境温度为20 ℃,装药初始温度分别为-30 ℃、-40 ℃、-50 ℃和-60 ℃时的发动机温度场变化特性进行多工况分析,结果如图4所示。

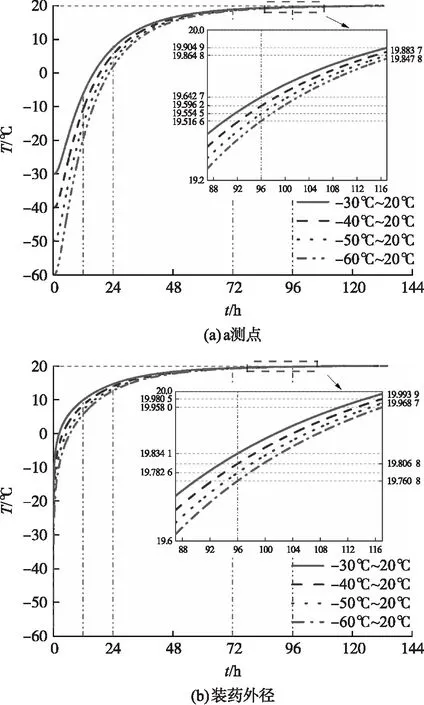
图4 初始温度对发动机内部温度的影响Fig.4 Temperature changes at different initial temperatures

由图4可知,当环境温度相同时,升温过程中装药初始温度越高,各点温度越高,升温速率越小。在起始的72 h内,装药温度上升速度较快,各工况间温度差较大。随着时间推移,发动机温差越来越小,当t=96 h时,不同工况下a测点和外径位置处的温度均接近环境温度,温差最小分别为0.037 9 ℃和0.021 8 ℃。当装药初温增加10 ℃时,装药特征点达到19 ℃所需时间最多减少了2.44 h。表2和表3分别为发动机不同初温条件下,a测点和外径位置处各个时刻的温升速率,可进一步分析发动机内温度场的变化规律。

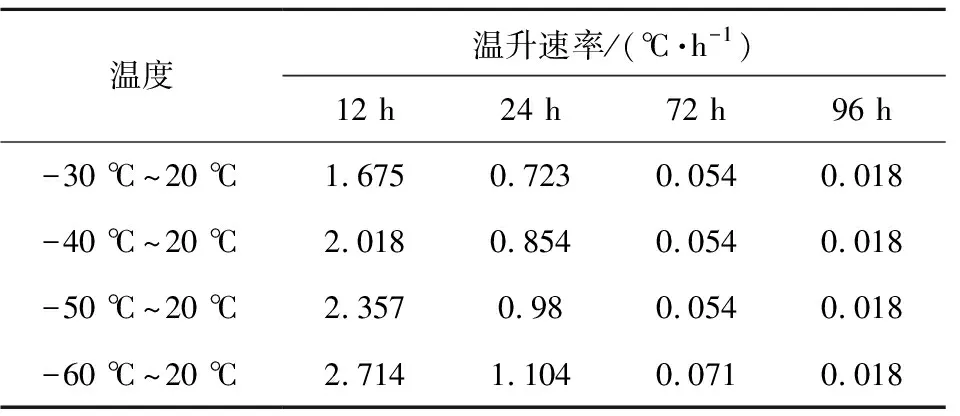
表2 不同初温下a测点温升速率Table 2 Temperature rise rate at the a measurement point with different initial temperatures

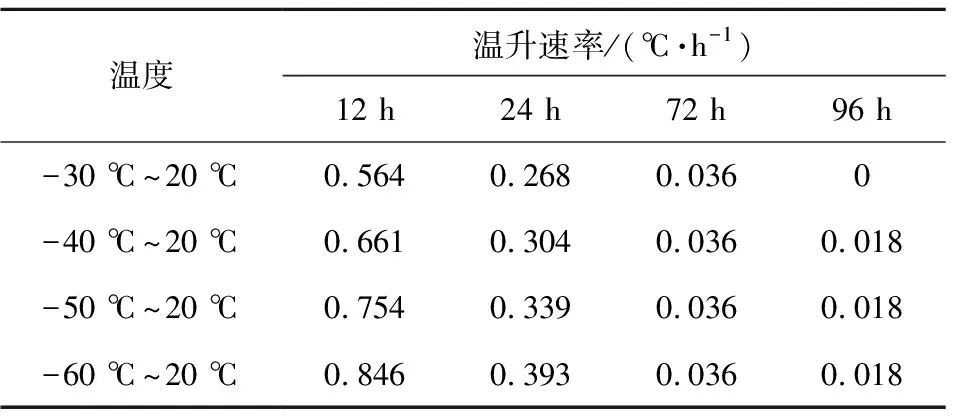
表3 不同初温下装药外径温升速率Table 3 Temperature rise rate at charge outer diameter with different initial temperatures

由表2可知,t=12 h时,各工况的温升速率均大于1.5 ℃/h,初始温度越低,温升速率越大。随时间推移,各工况的温升速率开始减小,t=72 h时温升速率将至0.072 ℃/h以下,此时初始温度为-60 ℃的温升速率仍为最大。t=96 h时,不同初温工况下的温升速率均为0.018 ℃/h,此时各工况测点温度均接近环境温度,因此温升速率也接近。

由表3可知,装药外径的温度变化规律与a测点相似。由于装药外径处壳体材料的导热系数较大,传热量越大,温升速率更快。结合图4(b)可知,在t=12 h时,装药外径处4种工况下与环境最大温差达到14.31 ℃,a测点4种工况下与环境最大温差达到39.42 ℃,装药外径处温度在变化初期迅速上升,缩小与环境的温差,使得温升速率在温度变化后期较小。

为了探究升温过程中,环境温度对其温度场的影响规律。针对装药温度为-40 ℃,环境温度分别为30 ℃、20 ℃、10 ℃和5 ℃时的发动机温度场变化特性进行分析,结果如图5所示。

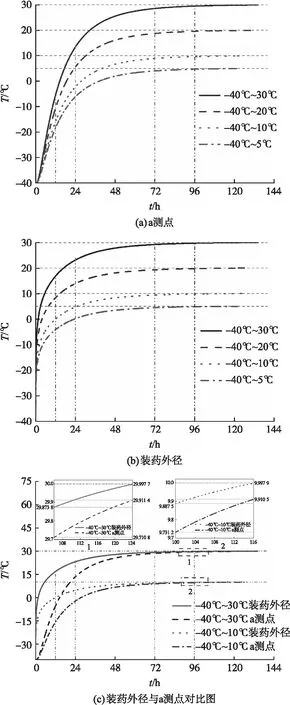
图5 不同环境温度下不同测点的温度变化Fig.5 Temperature variation at different ambient temperatures

由图可知,当装药温度相同时,环境温度越高,升温过程中各点温度越高,温升速率越大。可以看出,在起始72 h内装药温度上升速度较快,各工况间温差较小。随着时间的推移,不同工况下的发动机内温度均已经接近环境温度。通过图5(c)可知,当t=2 h、环境温度分别为10 ℃和30 ℃时,a测点的温升速率分别为1.906 ℃/h和2.805 ℃/h,此时装药外径处对应的温升速率分别为2.769 ℃/h和3.83 ℃/h,明显大于a测点的温升速率。这是由于温度变化初期,装药外径处壳体材料的导热系数大于推进剂的导热系数,传热量大,温度上升速率快。随着升温过程的继续,装药外径与环境间的温度差减小,温升速率明显小于a测点。当环境温度为30 ℃时,两处装药特征点达到29 ℃所需时间相差14.42 h,当环境温度为10 ℃时,两处装药特征点达到9 ℃所需时间相差3.82 h。表4和表5分别为不同环境温度条件下发动机内温度场的变化规律。

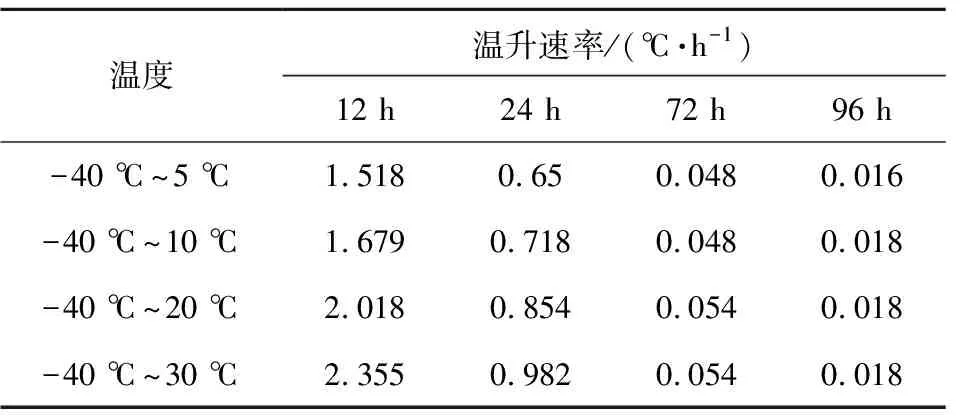
表4 不同环境温度下a测点温升速率Table 4 Temperature rise rate at the measurement point of a with different ambient temperatures

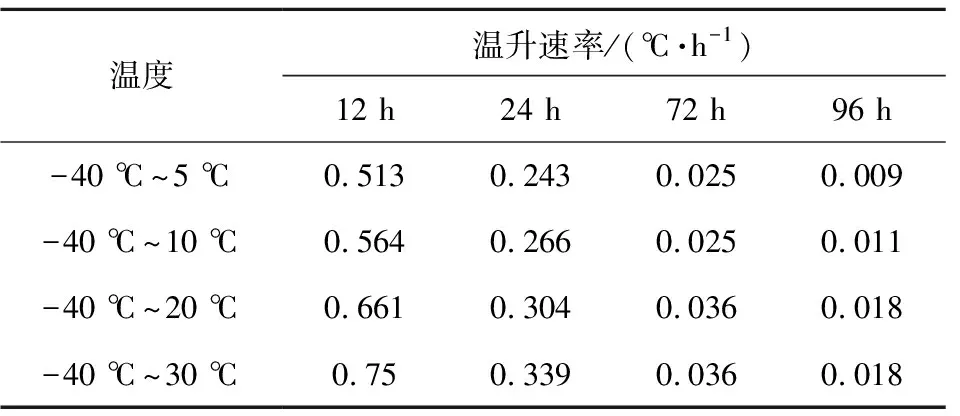
表5 不同环境温度下装药外径温升速率Table 5 Temperature rise rate of charge outer diameter with different ambient temperatures

由表4可以看出,t=12 h时,温升速率均大于1.5 ℃/h,环境温度越高,温升速率越快。随试验时间推移,各工况下温升速率开始减小;t=72 h时,各工况下的温升速率都小于0.054 ℃/h,此时环境温度为30 ℃的发动机的温升速率仍为最大;t=96 h时,不同环境温度工况下的温升速率均较小。

结合图5可以看出,温度变化初期温差越大,温升速率越快,经过较长时间,各工况的装药温度与环境温度的温差减小,温升速率减小直至为0 ℃/h,最终与环境温度一致。

在t=12 h时,装药外径处4种工况下与环境的最大温差为13.136 ℃,a测点4种工况下与环境的最大温差为35.446 ℃;t=96 h时,装药外径处的装药温度与环境温度最大温差仅为0.23 ℃,此时a测点的装药温度与环境温度最大温差为0.47 ℃。

2.2.2 温降过程分析

为了探究降温过程中,发动机内装药初始温度和环境温度对其温度场的影响规律。针对不同装药初始温度不同环境温度进行分析,结果如图6所示。

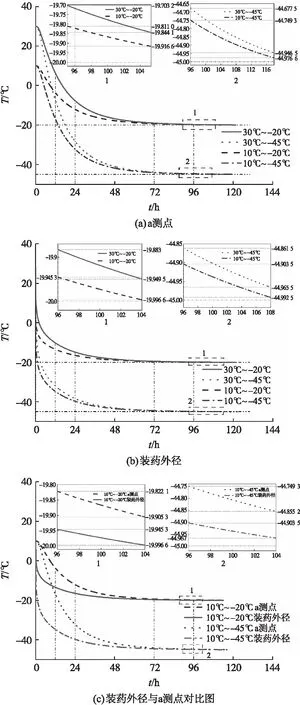
图6 不同边界条件下不同测点的温度变化Fig.6 Temperature variation at different measurement points under different boundary conditions

由图6可知,在起始的72 h内,装药温度下降速度较快,随着装药温度的下降,两测点处温度变化均较为平缓。这是由于各工况下发动机内温度均接近环境温度,温差越小传热越慢。通过图6(c)可知,温度变化初期两种工况下a测点温度变化较为平缓,装药外径温度变化迅速。这是由于装药外径的壳体导热系数大,温度下降快,温度变化后期装药温度非常接近环境温度,使得发动机内装药温度需要较长时间与环境温度达到完全平衡。当环境温度为-20 ℃时,两处装药特征点达到-19 ℃所需时间相差3.38 h,当环境温度为-45 ℃时,两处装药特征点达到-44 ℃所需时间相差3.28 h。表6和表7为不同边界条件下,装药1/3和外径位置处各时刻的温升速率。可知,同一时刻同一测点处,装药初始温度与环境温度温差越大,温度变化速率越大。对比10 ℃～-20 ℃和10 ℃～-45 ℃这两种工况下同一时刻不同测点处温升速率可知,由于装药外径处壳体材料的导热系数大于推进剂的导热系数,t=2 h时装药外径的温度变化速率大于a测点;随着降温过程的继续,当t=96 h时,温度变化速率接近于0 ℃/h,这是由于后期装药温度非常接近环境温度,传热量减少,温升速率较慢,因此发动机内各点温度与环境温度达到完全平衡需要较长时间。

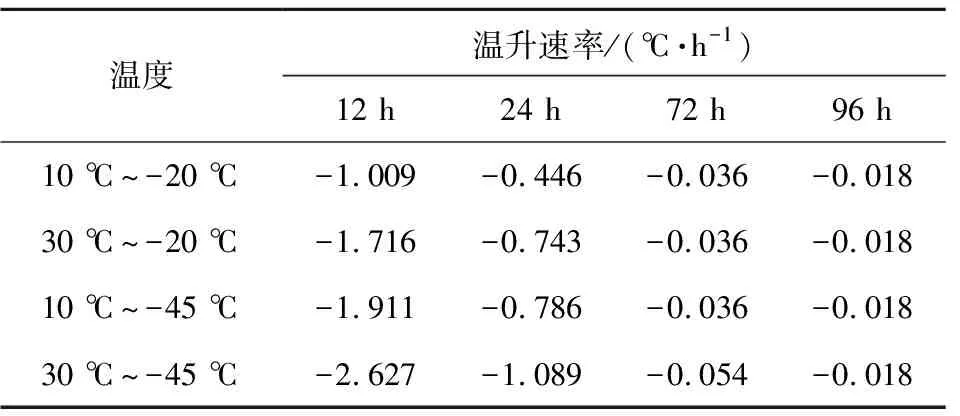
表6 不同边界条件下a测点温度变化速率Table 6 Temperature change rates of measurement point a under different boundary conditions

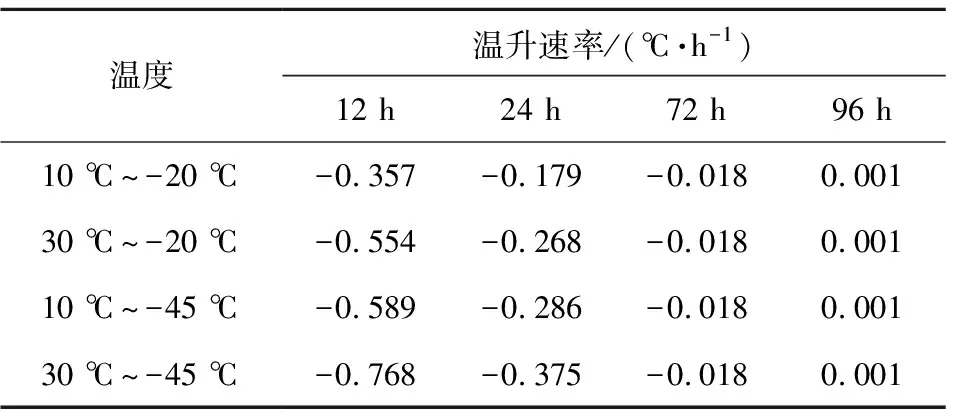
表7 不同边界条件下装药外径温度变化速率Table 7 Temperature change rate of charge outer diameter under different boundary conditions

3 结论

①通过某口径火箭发动机多层材料在不同边界条件下装药温度场与环境之间的数值计算与实验结果的对比,验证了所建立理论模型能够准确描述装药温度场的温度变化特性。

②由于壳体与推进剂的导热系数的不同,装药外径的壳体导热系数大于装药内侧,使得温度变化初期装药外侧温度变化波动较大,装药内侧温度变化较为平缓,随测试时间的增长,整个装药温度场终将趋于平衡状态。

③同一时刻同一测点,固定装药初温或者环境温度时,温差越大,温度变化速率也就越大;而同一时刻不同测点的温度变化速率与材料的导热系数相关。

④温差是热量传递的动力,热量的传递与物体内部温度分布状况密切相关,多层材料发动机装药和环境的初始温差越大,发动机内各点与环境温度达到完全平衡的时间越长。