能量优化分配再入轨迹快速规划方法
薛光伟,辛万青,傅 瑜
(1.北京宇航系统工程研究所,北京 100076;2.中国运载火箭技术研究院,北京 100076)
升力式再入飞行器是一种由火箭发动机助推到一定高度、速度后,利用气动升力在大气层内进行远距离无动力飞行的新型飞行器,具有速度快、机动能力强、飞行距离远等优点,受到各国的广泛关注。飞行器在再入过程中面临着诸多干扰,包括参数和环境的不确定性、可能存在的敌对拦截,需要不断进行轨迹调整,甚至是博弈对抗。因此,为了提高飞行器应对干扰拦截的能力、减小能量消耗,合理规划飞行器能量沿再入轨迹的分布具有重要意义。
升力体再入轨迹规划最早起源于航天飞机的再入制导问题。HARPOLD等[1]在1979年详细介绍了航天飞机的轨迹规划方法,首先基于热防护需求确定攻角-速度剖面,然后将过载、热流等约束转化为阻力加速度-速度(D-E)剖面上的再入走廊,在走廊内进行轨迹规划。这种规划方法被后续许多学者进一步继承和发展。文献[2]在D-E剖面内通过再入走廊的上下边界插值得到轨迹,通过调节插值系数和倾侧角翻转位置满足射程和航向约束。文献[3]直接在高度-速度(H-V)剖面内进行规划,考虑了飞行路径角的变化,获得了更加准确和直观的轨迹。文献[4]通过谱分解把能量变化曲线拟合为二次多项式,推导得到模型解析解,进而通过规划倾侧角幅值和翻转时机满足纵向约束与横侧向约束。上述方法都需要预先确定攻角剖面,采取可以解析计算的曲线形式,曲线参数根据飞行热流约束确定。
文献[5]基于准平衡滑翔条件,推导了以航程为自变量的解析公式,通过滑翔起、终点约束条件和禁飞区分布,直接求解攻角倾侧角曲线。文献[6]假设高度随能量线性变化,将D-E剖面轨迹设计为二次函数,将轨迹约束转化为攻角约束,在约束范围内通过调节攻角扩大再入走廊的范围。文献[7]推导了射程、高度和速度的解析公式,通过调整平衡滑翔的高度满足末端速度需求。文献[5-7]提出的规划方法中,攻角剖面的设计更加灵活,但面临从再入起点开始就在为满足末端约束而调整轨迹的问题。当目标射程小于最大可达射程时,多余的能量将分散在再入全程消耗,当飞行器遇到未知干扰拦截时,前期消耗的能量将会降低其调节能力。
文献[8]基于最优化理论和简化模型,推导了存在禁飞区情况下耗能最小的飞行轨迹。文献[9]针对升力飞行器全程轨迹优化问题提出了多种规划方法。文献[8-9]中的轨迹能量优化以飞行过程能耗最小、终点速度最大为优化目标,不适用于处理终点速度给定下的能量优化分配问题。文献[10]研究了存在终点速度约束时的机动轨迹规划问题,通过对经由点位置和速度进行搜索规划,优化了轨迹前后段的能量分配。这种方法通过神经网络对飞行器的机动能力进行预测,预测的准确度取决于样本库与神经网络学习效果。
近年来,越来越多的学者尝试将轨迹规划转化为轨迹优化问题,通过数值方法进行求解。文献[11]将轨迹分段,利用分段高斯伪谱法对轨迹规划问题进行求解。文献[12]利用伪谱法将轨迹规划离散为NLP问题后,通过无损凸化技术将问题转化为凸优化问题,提高了求解效率。文献[13]针对二维平面内的简化模型,通过引入指数衰减的信赖域宽度和惩罚系数上界,改进了基于伪谱凸优化的弹道规划算法的稳定性。文献[14]推导了高度和剩余射程的函数关系式,将轨迹规划问题转为在特定剩余射程处的高度设计问题,基于改进的粒子群算法设计了一种协同轨迹的快速规划方法。这些数值方法通过合理设计优化目标,能够得到满足特定性能需求的轨迹,但针对飞行器复杂的非线性模型时,求解算法的稳定性和快速性仍存在一定问题。
为提高飞行器应对未知干扰拦截的能力,本文提出了一种能量优化分配轨迹(Energy Allocation Optimized Trajectory,EAOT),将EAOT分为三段:初始下降段、能量最优段和能量管理段。EAOT与现有文献中的轨迹的主要区别在于,不再把多余能量分散消耗到飞行全程,而是集中在飞行后期的能量管理段,从而使能量最优段具有尽可能多的能量应对干扰。本文设计了初始下降段、能量最优段的规划方法,推导了能量管理段最短射程解析计算公式,在此基础上提出了一种迭代算法,用于求解能量最优段与能量管理段的平滑切换位置。最后,构建了EAOT一体化生成方法,并通过仿真分析验证了EAOT对于干扰拦截的适应性,以及所设计规划算法的有效性和快速性。
1 再入模型与轨迹分段
1.1 再入数学模型
考虑地球偏心率和自转的影响,建立飞行器再入数学模型如下:
(1)
式中:V为相对大地的速度,γ为飞行路径角,ψ为航向角,r为从地心到飞行器质心的距离,θ为经度,φ为地心纬度;m为飞行器质量,gr为引力加速度沿地心矢径方向的分量,gωe为引力加速度沿地球自转角速度方向的分量,ωe为地球自转角速度,D为气动阻力,L为气动升力,σ为倾侧角。
气动阻力和升力的计算公式如下:
(2)
式中:Aref为飞行器参考面积;Cd、Cl分别为气动阻力系数和气动升力系数;ρ为大气密度,可采用指数函数形式进行近似计算:
ρ=ρ0exp(-H/HC)
(3)
式中:ρ0为海平面大气密度常数,H为飞行器海拔高度,HC为标准高度。
1.2 轨迹分段设计
再入轨迹从再入点开始,到下压段为止。本文提出的EAOT将再入轨迹分为初始下降段(Initial Descent Phase,IDP)、能量最优滑翔段(Energy Optimal Phase,EOP)和能量管理段(Energy Manage Phase,EMP),如图1所示。AB段为IDP,飞行器在这一段从再入起始状态平稳过渡到滑翔飞行状态;BC段为EOP,飞行器在该段按照能量最优轨迹飞行,使得遇到未知干扰拦截时,拥有更多能量用于调整轨迹;CD段为EMP,飞行器在该段需消耗多余的能量,调整状态至满足再入终点的射程、高度、速度及航向角约束。
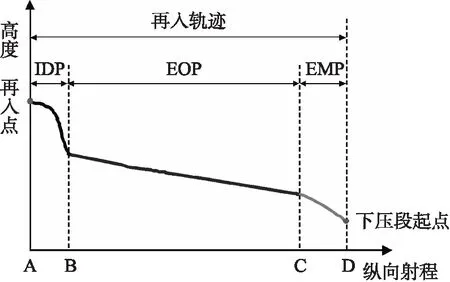
图1 能量优化分配轨迹分段示意图Fig.1 Phases of energy allocation optimized trajectory
在IDP阶段,飞行高度较高,大气密度小,控制力较弱,因此采用固定攻角和零倾侧角飞行模式。同时为了尽快拉平轨迹,为后续飞行创造较好的条件,采用最大攻角飞行。
飞行器在EOP段按照能量最优轨迹飞行。由文献[15]可知,当初、末能量确定时,飞行器平衡滑翔射程主要取决于飞行过程中的升阻比,升阻比越大,射程越远。飞行器的能量在飞行过程中单调递减,射程最远代表飞行过程中能量消耗最慢,最大升阻比对应的轨迹为能量最优轨迹。因此,EOP以最大升阻比攻角飞行。
EMP是再入轨迹的最后一个阶段,其任务是调整飞行器的能量,使其满足再入段到下压段的交班条件,主要包括射程、高度、速度和航向角等方面的约束。为实现能量的优化分配,EOP射程应尽可能长,EMP需在最短的航程内完成能量耗散。因此,EAOT规划的核心是确定EOP和EMP的切换位置。
1.3 能量管理段射程解析解
为使EOP射程最长,EMP射程需取最小值。EMP最小射程的实质是在起、终点的高度和速度给定的条件下,飞行器采用平衡滑翔方式所能实现的最小射程。
为了分析EMP的射程,对式(1)所示的再入模型进行一定简化。EMP射程较短,可近似忽略地球偏心率和自转。考虑到无动力飞行的过程中,飞行器的能量单调递减,且直观反映了飞行器的飞行能力,选择能量作为自变量。以无穷远处为势能零点,定义飞行器单位质量的能量E:
(4)
式中:μ为地球引力常数。
将能量对时间微分,可得:
(5)
将式(5)代入式(1),忽略地球偏心率和自转的影响,得到以能量为自变量的飞行器模型:
(6)
式中:g为不考虑地球偏心率的地球引力加速度。
飞行器的轨迹长度微元dS可分解在极坐标系的三个方向上,并存在如下关系:
(7)
将式(6)代入式(7),可化简得到轨迹长度相对于能量的微分:
(8)
假设EMP起点处的能量为E1,速度为V1,高度为H1;终点处能量为E2,速度为V2,高度为H2。则EMP的轨迹长度SEMP可由式(8)积分为
(9)
将式(2)和式(3)代入,整理得:
(10)
为了降低控制难度,减小峰值热流,再入飞行器需要满足平衡滑翔条件,即飞行路径角γ保持为一个较小的常数γ*[16],此时可近似认为高度和速度随能量线性变化[6]。当EMP初、末状态确定时,高度和速度随能量的变化关系也随之确定。假设高度随能量线性变化的关系式为
H=kE+b
(11)
(12)
将式(4)、式(11)和式(12)代入式(10)可得:
(13)
设a=E+μ/r,并认为r在飞行过程中基本保持不变,有:
(14)

(15)
此级数的收敛条件是a为实数且a≠0,这一条件在轨迹规划问题中一般均可满足。为进一步分析此级数的收敛速度,选取4组不同长度的SEMP。将通过数值积分计算得到每个SEMP的准确值,与不同阶数的级数近似计算结果进行对比,结果如表1所示。从表中可以看出,20阶级数的计算结果误差不超过10 m,10阶误差不超过100 m。具体分析时,可以根据实际精度需求选取不同阶数。

表1 不同SEMP的积分计算和级数近似结果Table 1 Compute results of integration and progression for different SEMP
至此,即可得到EMP轨迹长度的近似解析计算公式:
(16)
式中:p为根据精度需求选取的级数阶数。
需要注意的是,式(16)只用于轨迹长度的初步估算,轨迹积分依然采用较为精确的式(1)进行求解。
2 再入轨迹快速规划
2.1 初始下降段
再入起点并不满足平衡滑翔条件,因此需要通过IDP的调整,使飞行器平稳过渡到平衡滑翔状态。设置倾侧角为零,攻角为最大攻角,对轨迹进行积分,检测飞行器状态是否满足如式(17)所示的平衡滑翔条件。当条件满足时,切换到EOP。
(17)
2.2 能量最优段
采用最大升阻比攻角α1飞行,为了更平稳地进行平衡滑翔,参考文献[15,18],采用一种轨迹震荡抑制技术,在标准攻角上附加调整攻角:
(18)
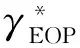
如果目标射程等于最大射程,EOP结束后没有多余能量,不需设置EMP,飞行器直接进入下压段;如果目标射程小于最大射程,EOP结束时飞行器的状态不满足再入终点约束,必须通过EMP调整。记录按照最大升阻比飞行至再入终点的轨迹,称为能量最优轨迹,其上某一点将作为EMP的起点,如图2 所示。
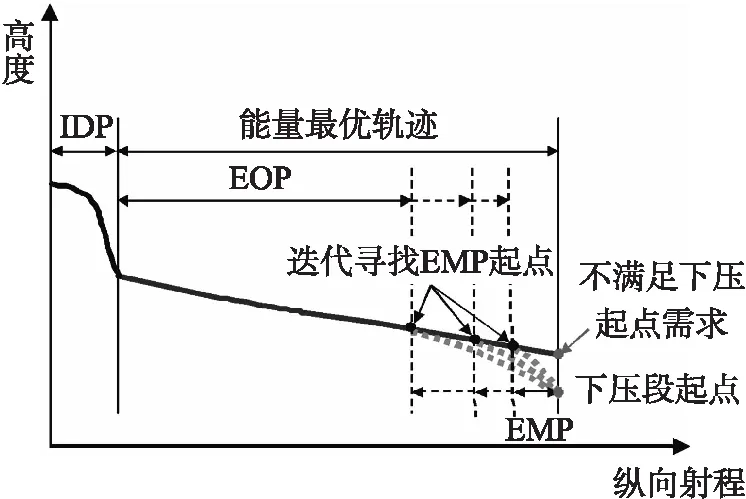
图2 能量最优段轨迹示意图Fig.2 Schematic diagram of energy manage phase
2.3 能量管理段规划方法
由2.2节分析可知,EMP射程与起点位置互相影响,本文提出一种迭代方法进行求解,结合倾侧角翻转技术构建了EMP轨迹快速规划方法。
根据几何关系求出飞行路径角:
(19)
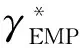
(20)
(21)

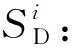
(22)
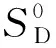


图3 倾侧角翻转位置规划流程Fig.3 Bank angle reversal location programming process
3 仿真分析
为了验证本文提出的EAOT轨迹性能及快速规划方法,将EAOT与固定攻角轨迹、最大射程轨迹进行对比。固定攻角轨迹在整个再入段按照零倾侧、分段固定攻角飞行,通过调整初始下降段攻角和平衡滑翔攻角满足再入终点约束。最大射程轨迹不考虑再入终点约束,初始下降段结束后始终保持最大升阻比攻角飞行。
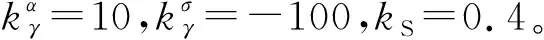

表2 仿真初末状态Table 2 The initials and final state of simulation
轨迹对比结果如图4~图6所示。其中,迭代得到从EOP到EMP的过渡点的纵向射程(归一化)为377.34,两次倾侧角翻转位置分别为382.15、388.61,最终到达位置为391.33。

图4 高度、速度、射程随时间变化Fig.4 Height,velocity and range change over time
从图4和图5可以看出,本文设计的EAOT轨迹满足了再入终点的各种约束。飞行器在EOP的速度相较固定攻角轨迹更慢,在EMP通过大攻角飞行快速降低速度,通过调整倾侧角维持飞行路径角稳定,迅速调整了飞行器状态,满足了再入终点的高度、速度和射程约束。横侧向通过倾侧角的两次翻转满足了横向误差和航向角约束。

图5 攻角、倾侧角、飞行路径角、航向角随时间变化Fig.5 Angle of attack,bank angle,fly path angle and heading angle change over time
从图5中可以看出,EAOT由于在前段保持了更快的速度,整个飞行过程的平均速度大于固定攻角轨迹,同等射程条件下总飞行时间少于固定攻角轨迹,这也是EAOT的一个优势。
图6的能量变化情况对比可以更清楚地体现出EAOT在轨迹能量分配方面的优点。与最大射程轨迹相比,固定攻角轨迹的能量从飞行起点开始就在以更快的速度衰减,整个飞行全程能量基本按照恒定的速率下降;EAOT在EOP能量下降速率较慢,与最大射程轨迹下降速率相同,是一种能量最优的飞行轨迹,在EMP迅速消耗了多余的能量。

图6 能量随时间和射程的变化Fig.6 Energy change over time and range
为了进一步分析EAOT轨迹的抗干扰效果,假设飞行器在飞行过程中遭遇了一次突发的干扰拦截,飞行器被迫进行了持续一段时间的机动,其间攻角保持最大攻角,倾侧角不断翻转。机动结束后,飞行器重新以当前位置为起点,规划新的EAOT轨迹继续飞行至终点。仿真结果如图7所示。
从图7中可以看到,飞行器在机动时消耗了能量,得益于前期节省的能量,仍然在终点处满足了终端的能量约束。相比于固定攻角轨迹,EAOT在飞行前段保留了更多能量,从而为飞行器适应未知干扰拦截提供了更好的能量条件。
4 结论
①本文提出了一种能量优化分配轨迹模式,把多余能量集中在能量管理段内消耗。通过仿真对比,证实这种轨迹增大了再入飞行前段的能量裕度,为飞行器在飞行过程中实时调整轨迹或提供了基础,提升了飞行器应对未知干扰拦截的能力。②本文推导了初末状态确定条件下的平衡滑翔最短射程的解析计算公式,在此基础上提出了能量管理段射程的快速迭代计算方法,结合倾侧角翻转技术,构建了能量优化分配轨迹的一体化生成方法,通过仿真验证了方法的可行性。③本文研究的轨迹快速规划方法,能够快速规划得到能量优化分配轨迹,可以满足飞行器遇到干扰拦截时轨迹在线重规划的实时性需求,具有较大的工程应用潜力。

