基于DENN的NSGA-II算法的串联多药室火炮内弹道性能优化

王 渤,罗 懿,薛 涛,张小兵

(南京理工大学 能源与动力工程学院,江苏 南京 210094)

超高速弹丸的发射装置是未来战争实现火力压制的重要技术[1-3]。为了在火炮压力上升幅度较小的情况下,大幅提升弹丸初速,国内外研究学者提出了大量新型火炮发射技术,比如底排装药技术[4]、随行装药技术[5]、整装液体药[6]、电磁轨道发射技术[7]、冲压发射技术[8]等。经过数十年的发展,这些新概念发射技术已经取得初步成果,但是受工业基础与技术水平的限制,尚未实现装备列装。

串联多药室发射技术[1]是提高弹丸初速的一种有效技术,它是在主药室燃烧到一定压力以后通过分隔两个药室的活塞对第二药室实行二次点火,产生压力接力作用,填补弹丸在膛内高速移动产生的低压区,形成并保持高压状态,从而达到提高弹丸速度的目的。串联多药室发射技术本质上是一种随行装药技术。但与传统的随行装药发射技术不同,串联多药室发射技术将随行药与主装药间通过活塞分开,避免了传统随行装药发射技术中的可靠随行以及高燃速火药研制等难题。与基于液体随行装药技术不同,由于串联多药室发射技术基于更为成熟的固体发射药,大大降低了实际过程中由于储存液体发射药导致的应用难度。此外,串联多药室技术可以不改变炮尾结构,通过更换身管或对现有火炮身管进行改造实现,对于整个火炮发射系统设计来说,可降低研制经费,具有实现装备化的潜力。

现阶段,从实验角度研究串联多药室发射“内弹道性能优化技术”已经取得一定成果,然而实验研究受限于发射过程的复杂性,尚未解决串联多药室发射过程的重要技术难题,比如副药室点火时刻、双药室内弹道匹配等。而从数学模拟方法分析串联多药室发射技术实现了多药室内弹道过程的“被动”建模,即已知内弹道参数,计算多药室内流场,预测弹丸初始速度。但受限于装药结构的复杂性,尚未实现对串联多药室发射内弹道参数设计,以及对弹丸初速和最高膛压的“主动”优化。

本文围绕串联多药室发射技术内弹道性能开展优化与分析。基于经典内弹道理论,在改进遗传算法(NSGA-II)算法框架内[9-10],提出结合差分进化(DE)算法[11]与神经网络(NN)模型[12]预测Pareto前沿的新思路。通过神经网络预测地Pareto前沿解指导NSGA-II算法初始种群的产生,实现了对串联多药室火炮内弹道性能的高效率、高精度优化。

1 串联多药室火炮内弹道建模与分析

1.1 物理过程

如图1所示,串联多药室火炮的物理结构主要包括主药室、点火管、副药室、活塞和弹丸。串联多药室火炮内弹道过程分为3个阶段:①点火具点燃主装药床,主药室产生高温高压气体,达到启动压力后,主药室气体推动活塞、副药室和弹丸一起运动。②达到设定的点火延迟时间后,点燃副药室。此时,副药室产生的火药气体压力小于主药室火药气体压力,因此主药室高压气体仍然推动活塞、副药室和弹丸一起运动。③当副药室的压力上升至与主药室与副药室压力差相同时,活塞和弹丸分离,此时主药室压力处于下降阶段,副药室压力处于上升阶段,主副药室压力差不断减小,副药室燃烧产生的高温高压气体推动弹丸向前运动[1]。

图1 串联多药室火炮结构Fig.1 Schematic of series multi-chamber gun

1.2 数学模型

根据经典内弹道模型的假设[3],建立串联多药室火炮内弹道方程组如下:

①采用多孔火药的内弹道模型,形状函数可以表示为

(1)

式中:Z为已燃火药相对厚度,Zk为火药燃烧结束后已燃火药的相对厚度,Ψ为火药已燃百分数,χ、λ、μ、χs、λs为火药形状特征量。

②燃速方程

(2)

式中:t为时间,2e1表示火药弧厚,p为平均压力,n、u1表示燃烧定律中的燃速指数和燃速系数。

③弹丸与活塞的速度方程

(3)

式中:vd为弹丸速度,ld为弹丸行程长,vh为活塞速度,lh为活塞运动距离。

④ 运动方程

第一阶段和第二阶段:

(4)

第三阶段:

(5)

式中:mh、md分别为活塞和弹丸质量,w2为副药室装药质量,p1为主药室平均压力,p2为副药室平均压力,φ为次要功系数,s为炮膛断面面积。

⑤能量方程

第一阶段,副药室未点燃,主药室能量方程:

(6)

第二阶段,主药室能量方程和第一阶段相同,副药室能量方程如下:

(7)

第三阶段,主、副药室能量方程如下:

(8)

式中:w1为主药室装药质量,l1ψ和l2ψ分别为主、副药室容积缩径比,ψ1和ψ2分别为主、副药室火药已燃百分比,va为弹丸活塞分离时活塞的速度,W1为弹丸活塞分离前主装药燃气对活塞、副药室和弹丸所做的功的总和,W2为分离后主药室对活塞做的功,W3为分离后活塞对副药室做的功,详细公式见[1,3]。

1.3 数值模拟

本文采用4阶Runge-Kutta算法,对串联多药室内弹道模型进行求解。结合串联多药室火炮与100 mm火炮的结构特点[1,13],选取内弹道起始参数见表1,其中V1与V2分别表示主、副药室容积,火药类型为七孔火药。计算结果如图2所示,最大压力366.4 MPa,弹丸初速为1 934 m/s。数值仿真得到的主副药室压力变化规律和弹丸活塞速度变化规律符合串联双药室火炮的实际情况,具有一定的可靠性。

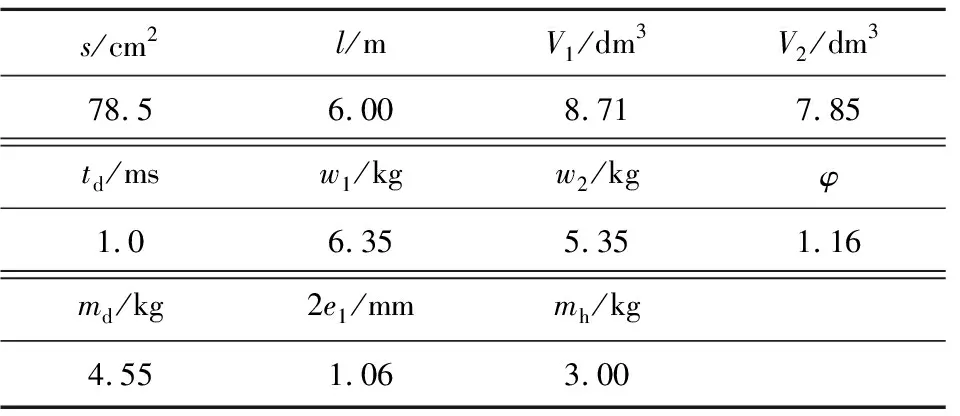
表1 初始参数表Table 1 Initial parameter list

图2 主副药室压力变化规律和弹丸/活塞速度变化规律Fig.2 Varialion of pressure in main and auxiliary chambers and velocity of projectile and piston

1.4 影响串联多药室内弹道性能因素分析

本文主要考虑主药室装药质量、副药室装药质量、活塞质量、点火延迟对串联多药室内弹道性能的影响。基于表1初始参数,通过固定变量法,分析数值计算结果。

①主药室装药质量影响

保持副药室装药质量不变,主药室装药质量增加时,主药室燃烧速度加快,主药室压力上升速度增加,弹丸加速度增加,副药室压力上升速度随着增加,弹丸出炮口的速度增加,其中身管内最大压力增加比值大于速度的增加的比值。因此,在一定范围内增加主药室装药质量,可以加速主药室燃烧,提升炮口初速。然而,当主药室装药质量增加到一定值,身管内最大压力急剧上升,身管受高温高压导致使用寿命降低,经济效益降低。

②副药室装药质量影响

保持主药室装药质量不变,副药室的装装药质量在一定范围内增加。该过程对弹丸未与活塞分离时,活塞和弹丸速度大小的影响较小。当弹丸与活塞分离后,副药室装药质量增加,压力上升随之增加,弹丸加速度也增加,弹丸出炮口的速度增加。当副药室装药质量远大于主药室装药质量时,相当于副药室作为单药室发射弹丸,这时候串联药室第一阶段推进过程不产生作用。由该表可知,合理的提升副药室的装药质量,可以在最大平均压力增幅较小的情况下,较大程度的提高炮口初速。

③活塞质量影响

保持其他参数保持不变,当活塞质量与弹丸质量的比值较小时,弹丸速度增长较快,副药室压力上升速度降低。当活塞质量与弹丸质量的比值过小时,副药室还未完全燃烧,弹丸就飞出身管,接力效果变差。此外,由第三阶段主、副药室能量方程(式(8))可知活塞在第三阶段会有一段时间减速,若主副药室压力相差过大,甚至可能会出现减速为0后,反方向加速的情况,该情况可能会导致药室结构受损。当活塞质量与弹丸质量的比值过大时,弹丸速度上升过慢,主药室燃烧增快,压力上升增快,主药室压力曲线过尖,身管内最大压力大幅增加,身管寿命缩短,经济效益降低。

④点火延迟时间影响

保持其他装填条件不变,仅改变点火延迟时间。在达到点火延迟时间后,点燃副药室,对弹丸的加速过程起一个接力的效果,如果点火延迟时间过短,弹丸的主副药室接近同时点燃,副药室压力上升过快,不能起到接力推进的效果。在一定范围内降低点火延迟的时间,副药室峰值右移,可以更充分的燃烧,提高弹丸炮口初速。

2 传统NSGA-II内弹道性能优化

串联多药室内弹道性能的优化是一类多目标问题。本节基于100 mm火炮作为研究对象,内弹道参数选取同表1,采用串联双药室结构装药,发射质量为4.55 kg的弹丸,考虑点火延迟时间、装填参数、弹丸活塞质量比作为内弹道优化过程的设计变量。

根据内弹道优化设计变量的取值要求,选用不需要编码译码的NSGA-II实数制编码;初始种群在内弹道设计变量取值范围内随机取值;在目标函数里添加约束条件,对于最小化情况,将不满足约束条件的个体适应度函数值设为无穷大。图3给出了详细的算法流程图。

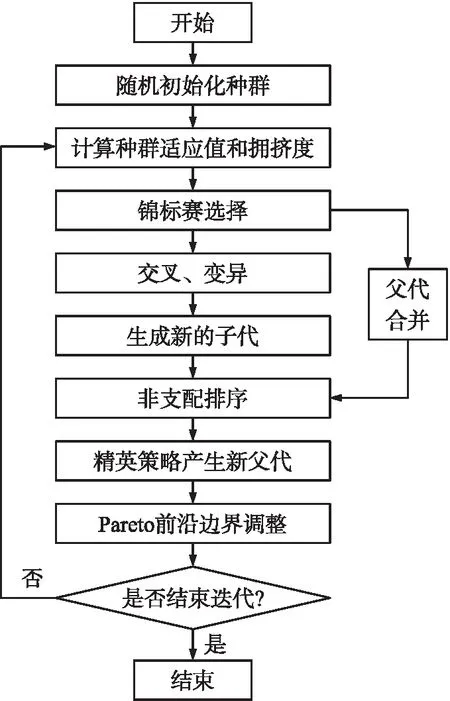
图3 NSGA-II算法流程图Fig.3 NSGA-II algorithm structure diagram

由于串联多药室发射过程十分复杂,基于NSGA-II串联多药室发射内弹道性能优化考虑活塞速度(vh>0 m/s)),炮口初速(vg>1 600 m/s),最大压力(pm<600 MPa)装填密度(0<Δ<0.85 kg/dm3)为约束条件。内弹道性能优化目标分别为最大压力pm、炮口初速vg。基于此,串联多药室的内弹道性能优化问题可转换为如下优化问题:

(9)

式中:优化变量为x=(x1x2x3x4)。x1∈[5.2,7]、x2∈[4.5,6.3]、x3∈[2.0,8.0]、x4∈[0.5,3.0]分别表示主药室装药质量w1(kg)、副药室装药质量w2(kg)、活塞质量mh(kg)、点火延迟时间td(ms)。

根据优化经验,选择NSGA-II计算采用的参数。其中,变异率为0.1,交叉率为0.9,迭代500次,种群数量为200。表2为迭代完成时优化排名前10的个体。通过对比分析,选择合理的装填参数,100 mm串联药室火炮在最大压力为239 MPa时,可发射炮口速度为1 600 m/s的弹丸,实现了最大膛压小、炮口初速大的优化目标。

表2 排名前十的个体Table 2 The first tenth individuals

3 耦合DE与NN的NSGA-II内弹道性能优化

基于传统NSGA-II算法的串联多药室优化虽然取得一定的效果,但在优化过程中忽略了影响内弹道性能的次要因素,不能有效地发挥算法优化性能。因此,本节提出基于鲁棒性高、收敛速度快的DE与映射能力强的NN改进的NSGA-II算法,减少优化过程的计算时间,提高内弹道优化的效率。主要思路如下:

①对于优化内弹道最大压力f1、炮口初速f2的双目标优化问题f=(f1,f2),最优边界可以用三点表示,即f1最优的点,f2最优的点,0.6f1+0.4f2最优的点。寻找这三个点的过程是单目标优化过程,采用收敛速度快、计算复杂程度低的DE算法完成。

②随机产生1400组在约束范围内取值的内弹道参数,求取每一组参数对应的f1最优的点,f2最优的点,0.6f1+0.4f2最优的点。将内弹道参数作为样本的特征向量,表示最优边界的三点作为样本标签,为机器学习模型提供训练样本。

③采用全连接神经网络(Fully connected Neural Network,FNN)训练样本,获得内弹道参数和最优边界的“函数关系”。实现输入内弹道参数,即可得到FNN预测地最优边界(下文简称为“预边界”)的目标。

④根据机器学习的预测结果,在选定内弹道参数后,让NSGA-II算法在预边界附近产生初始种群,获得更为精确的最优边界,并判断该方式对多目标智能寻优算法是否起到了优化效果。

3.1 基于DE算法的串联多药室火炮内弹道单目标优化模型

DE算法属于启发式算法,它将潜在解保存为种群中的个体,通过模拟生物进化的过程来实现寻优。每一个DE迭代循环包含以下任务:随机选择进化池中的个体进行交叉、变异、自然选择,保存适应度高的个体组成新的种群。达到迭代代数前,反复采用上述方式更新种群,最终产生最优解。DE算法计算时间快、采用一对一竞争策略、全局收敛性强、鲁棒性高[12],适用于内弹道单目标优化。主要实现步骤如下:

①随机产生交叉变异个体

在应用DE算法对内弹道性能优化时,采用实数制编码,根据超参数随机生成一个数量为NP的种群,种群包含由潜在解构成的个体Xi=(x1x2…xn),每一个个体都是内弹道条件约束范围内的设计变量:Xi∈[Xmax,Xmin],其中Xmax,Xmin分别为设计变量的上边界和下边界。

②为初始种群分配适应度

分别根据内弹道目标函数,对种群中的每个个体进行评价。根据优化目标,选取三个目标函数如下:

(10)

③变异操作

DE随机选择两个个体作差分,将差分矢量与另外一个随机选择的个体相加,产生一个实验个体,实现过程如下:随机产生个体X1,X2,X3。

V=X3+F·(X1-X2)

(11)

式中:V为实验个体、F为缩放因子,F对算法的影响较大,更改F会影响算法的全局搜索性能。如果将F设置为一个较小值,算法对局部个体的搜索能力更强,但是更容易陷入局部最优解;如果将F设置为一个较大值时,种群多样性更高、全局寻优能力增强,但收敛速度会变慢。经过研究表明[13],F一般在[0,2]之间取值时能够达到较好的优化效果,通常取0.5。

④交叉操作

交叉操作是基于变异差分项进行的,交叉操作选用实验个体和其对应的父代个体进行交叉,其中产生的子代个体中,有至少一个向量分量来自于变异操作产生的实验个体,产生方式如下:

(12)

式中:CR表示交叉概率,在[0,1]范围内取值。randj(0,1)∈[0,1]是均匀随机数,jrand是随机选择的维度,用于确保子代个体向量Ci至少从变异个体Vi得到一个分量。该交叉方法称为二项式均匀交叉。

⑤选择操作

DE算法采用一对一竞争策略,将产生的子代与父代比较,选择更优解。竞争策略降低了DE算法的复杂性。在完成选择操作后,重复步骤②～⑤,满足终止条件后结束迭代。根据优化经验,交叉概率CR选择0.5,缩放因子F选择0.5,种群数量NP选择50,迭代次数选择50。采用表1中的内弹道参数,应用DE算法对f1、f2、f3三个目标函数进行寻优。如图4所示,DE算法收敛快,优化效果较好。

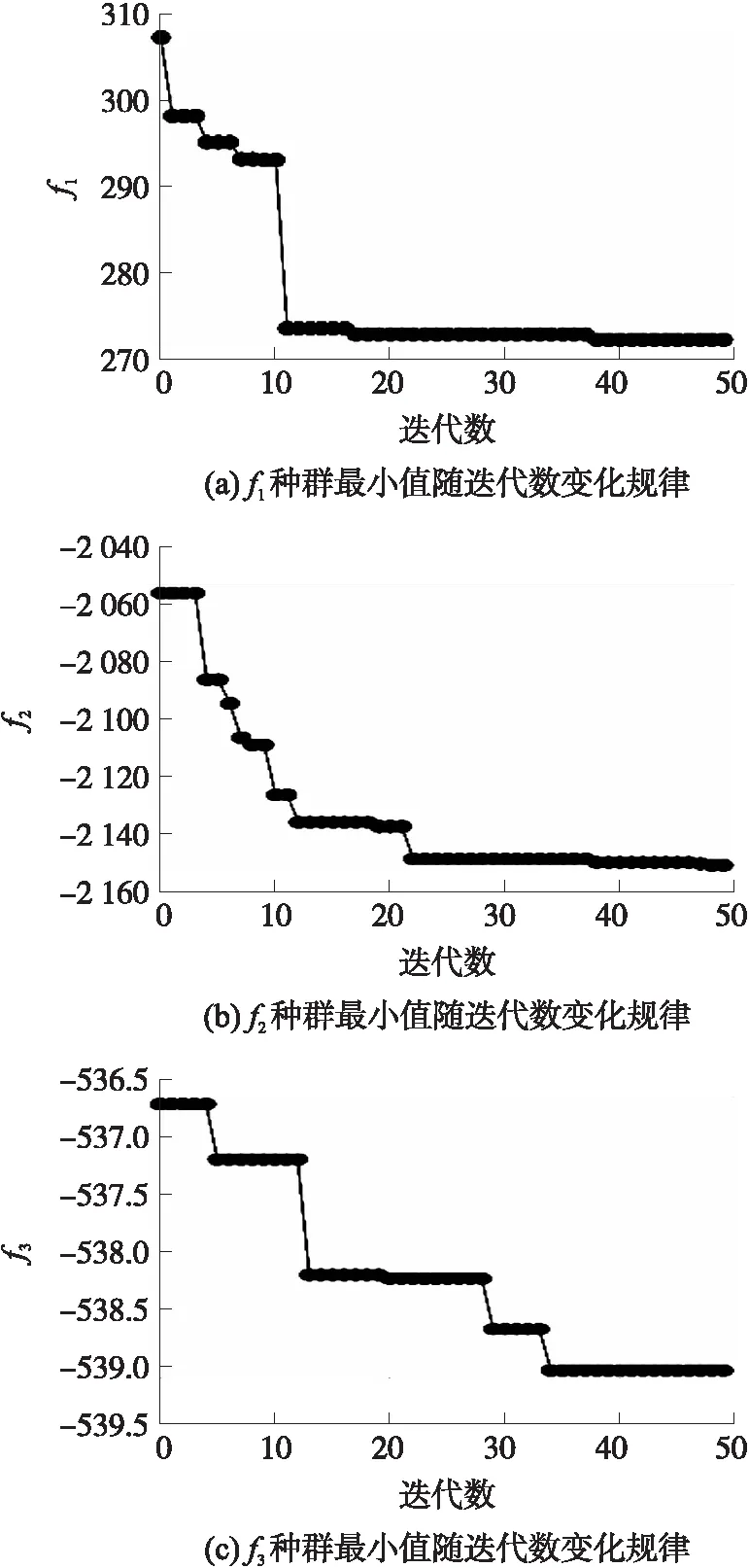
图4 目标函数随迭代数变化规律Fig.4 The change law of objective function with the number of iterations

3.2 串联多药室火炮内弹道性能深度学习预测最优边界

在多目标优化的群体智能算法中,初始种群都是随机产生的,本文创新性地提出了应用DENN指导NGSA-II初始种群的新方法,该方法可以加速NSGA-II的计算,提升内弹道优化效率。

①基于DE算法的内弹道优化样本获取

在基于传统NSGA-II算法的串联多药室火炮内弹道性能优化中,本文采用影响火炮内弹道性能的主要因素作为内弹道多目标优化的设计变量,包括主药室装药质量,副药室装药质量,活塞质量,点火延迟时间等。然而,在火炮发射过程中,影响炮口初速和最大压力等内弹道性能的因素还包括火药弧厚、弹丸行程长、弹丸质量、主药室容积、副药室容积、炮膛截面积等。这些是优化过程前,人为设置的内弹道参数,设置后为常值,尚未被有效地利用。采用机器学习方法,可获得内弹道参数与最优边界的“函数关系”。本文考虑的内弹道参数如下式:

X=(mdV1V2sl2e112e12)

(13)

式中:2e11为主药室火药弧厚,2e12为副药室火药弧厚。将X作为机器学习训练样本的特征向量,将代表最优边界的三个点Y=(Y1Y2Y3)作为样本标签,随机生成491组样本。Y通过DE算法获得。如图5所示,通过DE获得的Y值与和最优边界相互吻合。

图5 三点表示的最优边界Fig.5 Three points represent the optimal boundary

②基于NN的内弹道模型训练

本文采用全连接神经网络网络(FNN)训练模型,对样本的特征向量和标签值进行归一化,从而实现提高训练精度的目的。图6为全连接神经网络的结构图,它总共由3部分构成,输入层,隐藏层,输出层。每一层的神经元输入上一层神经元的向量,输出向量为经过加权和激活函数后的结果。隐藏层和神经元的数量会影响模型的拟合和泛化能力,可经过实验选取合适的数量。为防止训练过程梯度消失,增加网络稀疏性,加快反向传播速度,可选取合适随机梯度下降算法(SGD)作为优化算法,线性整流函数(ReLU)函数作为激活函数。详细的训练过程如下:选取内弹道参数作为神经网络的输入,最优边界作为神经网络的输出,采用均方误差(MSE)作为机器学习训练的损失函数,计算反向传播的梯度,更新神经网络的权重,直到模型收敛。

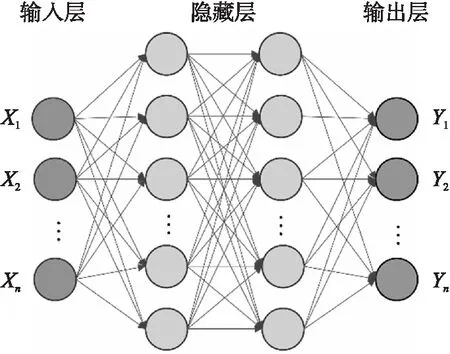
图6 全连接神经网络模型Fig.6 Fully connected neural network model

③机器学习优化结果

将491组样本按8∶1∶1的比例分为训练集、验证集、测试集。采用三层神经网络,隐藏层神经元数量为32。训练完成后,样本的MSE和相关系数R见表3。

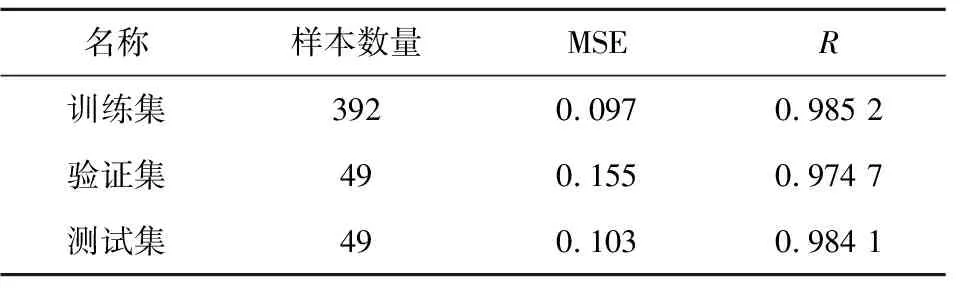
表3 训练集、验证集和测试集的MSE和RTable 3 MSE and R for training,validation and test sets

④串联多药室内弹道性能优化效果

保持约束条件与优化目标函数不变,选取方式同第2节。NSGA-II的初始种群分别在预测边界附近产生与随机产生,比较两种情况下NSGA-II算法的收敛速度和优化性能。数值仿真结果如图7所示,ML50g表示DENN-NSGA-II算法迭代50次,NS100g表示传统的NSGA-II算法迭代100次。数值仿真结果显示,机器学习改进的NSGA-II算法只需迭代50次,即可获得和传统的NSGA-II迭代100次性能相同的Pareto前沿。

4 结论

本文以100 mm串联多药室火炮为研究对象,分析了不同内弹道参数对弹丸初速和膛内最大压力的影响。采用了耦合DE与NSGA-II优化算法对内弹道性能进行优化,分析串联多药室发射技术的最优化内弹道参数组合。主要结论如下:

①数值计算结果表明主药室质量、副药室质量、活塞质量、点火延迟时间等对串联多药室火炮内弹道特性有一定的影响。

②采用传统NSGA-II算法对该火炮的内弹道性能进行了多目标优化。优化结果表明串联多药室火炮在最大压力为239 MPa时,可发射炮口速度为1 600 m/s的弹丸。

③基于DE算法和机器学习NN的NSGA-II算法能够有效地提高串联药室火炮的内弹道优化效率。数值测试表明,DENN-NSGA-II算法在迭代50次时能够得到与传统NSGA-II算法迭代100次相同的优化效果。