智慧教育环境中计算机辅助教学应用研究

张凯 覃正楚 况莹

摘要：随着科学技术的不断发展，在线教育逐渐被大众接受，促进了教育信息化的发展。但对于师生而言，教育信息化伴随着学习资源难以抉择、学习进度难以掌控等问题。智慧教育是解决这些问题的方法之一。智慧教育在人工智能技术的加持下，能够实时衡量学生的知识状态，为每个学生提供细粒度的教育服务，达到因材施教的效果。在智慧教育中，知识追踪的主要任务是从学生的历史数据中判断其知识状态，为细粒度教育服务提供知识状态的支撑。文章介绍了目前可供使用的国际公开真实教育数据集及常用的知识追踪模型，并将提出的模型应用于英语教学中，验证了模型的有效性。

关键词： 教育信息化；人工智能；智慧教育；知识追踪；教学应用

中图分类号：G642        文献标识码：A

文章编号：1009-3044（2023）13-0161-03

开放科学（资源服务）标识码（OSID）

0 引言

随着科学技术的不断发展，使用计算机辅助教学的在线教育逐渐被大众接受，加快了教育信息化的进程。在线教育产生了大量的教学数据，即教育大数据，但传统教育模式难以从教育大数据中衡量每个学生的知识状态，导致老师无法为学生提供细粒度的教育服务。因此，使用科学的方法或技术手段对教育大数据进行更深入的挖掘和分析是有必要的[1]。智慧教育使用人工智能技术对教育大数据进行挖掘分析，能够衡量学生的知识状态，进而为其提供细粒度的教育服务。其中，衡量知识状态的任务由知识追踪完成[2-4]。

1 传统教育模式与智慧教育模式的分析

1.1 传统教育模式

1.1.1 传统教育模式具有地理限制

开展教学活动必须满足三点要素：老师、学生以及教学场所。上述要素缺其一便无法开展教学活动。但在传统教育模式中，老师和学生只能在学校内开展教学活动，固定的教学场所导致传统教育模式失去灵活性。因此传统教育模式具有地理限制，导致此模式无法灵活地开展教学活动。

1.1.2 传统教育模式具有主观限制

教学活动的主体是老师和学生，两者都具有独立的主观意识。这种主观意识能够影响教学活动的质量，例如学生不喜欢老师的教学风格，导致无法更好的学习知识。但在传承教育模式中，师生关系一旦确定，便难以改变。因此传统教育模式具有主观限制，导致此模式无法满足每个学生的教育需求。

1.1.3 传统教育模式具有精力限制

作为教学活动的主体，老师和学生的精力也能够影响教育学活动质量。当老师对教学活动投入更多精力时，便能为更多的学生提供细粒度的教育服务；当学生对教学活动投入更多精力时，便能更积极主动地接受教育服务。但老师和学生的精力总是有限的，即老师难以为每个学生提供细粒度的教育服务，学生难以接受每个老师提供的统一教育服务。因此传统教育模式具有精力限制，导致此模式无法为每个学生提供细粒度的教育服务。

1.2 智慧教育模式

1.2.1 智慧教育模式能够打破地理限制的影响

智慧教育是教育信息化与人工智能技术相结合的产物，其主体仍是老师和学生。与传统教育模式相比，智慧教育模式使用计算机辅助教学，能够打破地理空间的限制，更加灵活地开展教学活动。因此智慧教育模式能够打破地理限制的影响，导致此模式能够更灵活地开展教学活动。

1.2.2 智慧教育模式能够消除主观限制的影响

智慧教育模式作为教育信息化的进一步发展，与传统教育模式相比，具有更丰富的教育资源，能够激发学生学习的积极性和主动性。例如学生A和B学习三角函数时，学生A更容易接受图形加公式讲解的授课方式，而学生B更容易接受直接讲解公式的授课方式。在传统教育模式中，两者的矛盾难以高效地中和；但在智慧教育模式中，丰富的教育资源能够同时满足两者的需求。因此智慧教育模式能够消除主观限制的影响，导致此模式能够满足大部分学生的教育需求。

1.2.3 智慧教育模式能夠减少精力限制的影响

随着科学技术水平的不断发展，MOOC、学堂在线、国家教育资源公共服务等多个在线学习平台都具有丰富的教育资源。一方面，学生在享受教育资源的红利时，也不得不花费更多的精力在做选择上；另一方面，老师在享受教育信息化的便利时，难以从教育大数据中衡量每个学生的知识状态，导致无法为每个学生提供细粒度的教育服务。智慧教育模式依托人工智能技术衡量每个学生的知识状态，能够有效地解决这一问题。因此智慧教育模式能够减少精力限制的影响，导致此模式能够为每个学生提供细粒度的教育服务。

2 教育数据集和知识追踪模型

在智慧教育模式中，知识追踪的主要任务是使用人工智能技术分析教育大数据，为细粒度教育服务提供知识状态的支撑，并预测学生未来答题的表现。

2.1 教育数据集

ASSISTment系列数据集由ASSISTment在线智能导学系统提供，是目前知识追踪领域内公开的最大的数据集。其中，ASSISTment2009数据集收集于2009-2010学年；ASSISTment2012数据集收集于2013-2013学年；ASSISTment2015数据集收集于2015年；ASSISTment2017数据集来源于该平台的教育数据挖掘挑战赛，就答题记录数量而言，ASSISTment2017数据集的可用数据密度是0.81，是该系列数据集中可用数据密度最高的数据集。

Slepemapy.cz数据集由Slepemapy.cz在线自适应系统收集，包含学生学习地理事实的答题记录。

Junyi Academy数据集由Junyi Academy在线教育网站于2015年收集。不同的是，该网站的学生即使选择了相同的习题，系统也可以给习题分配不同的数指，即该数据集中相同习题由不同的数值组成。

2.2 知识追踪模型

文献[5]提出了贝叶斯知识追踪（Bayesian Knowledge Tracing， BKT），是概率知识追踪模型中最具代表性的模型。该模型基于隐马尔可夫模型，通过初始学会某概念的概率[P（L0）]、未学会状态到学会状态的转移概率[P（T）]衡量学生的知识状态、未掌握概念但猜对的概率[P（G）]以及掌握概念但答错的概率预测未来的答题情况。

文献[6]提出了深度知识追踪模型（Deep Knowledge Tracing， DKT），首次将深度学习的方法应用在知识追踪领域中，使用循环神经网络或长短期记忆网络衡量学生的知识状态、预测未来的答题情况。

文献[7]提出了动态键值记忆网络（Dynamic Key-Value Memory Networks， DKVMN），受记忆增强网络的启发，构建了一个静态的键矩阵[Mk]存储概念的向量表示，一个动态的值矩阵[Mv]存储知识状态的向量表示。DKVMN根据前一时刻的知识状态和当前时刻作答的习题预测学生答题情况，即模型输入值矩阵[Mvt-1]和习题编号[qt]，输出学生正确回答该习题的概率[P（rt|qt）]；根据当前时刻的答题情况更新值矩阵[Mvt-1]至当前时刻，即模型输入习题编号[qt]和相应的答题情况[rt]，输出学生当前时刻的知识状态[Mvt]。

文献[8]提出了DKT-F （DKT + Forgetting）模型，在DKT的基础上，引入遗忘因素：距离上次学习相同概念的时间间隔、距离上次学习的时间间隔、学习相同概念的次数建模学生的遗忘行为。在衡量学生的知识状态和预测未来答题情况方面与DKT方法一致。

文献[9]提出了LFKT（Deep Knowledge Tracing Model with Learning and Forgetting Behavior Merging）模型。该模型也建模了遗忘行为，不同于DKT-F的是，LFKT还引入学生原本对该概念的掌握程度作为遗忘因素。在衡量学生的知识状态和预测未来答题情况方面与DKVMN的思想一致，分两个过程实现衡量知识状态和预测答题情况。

3 基于注意力机制的知识追踪模型

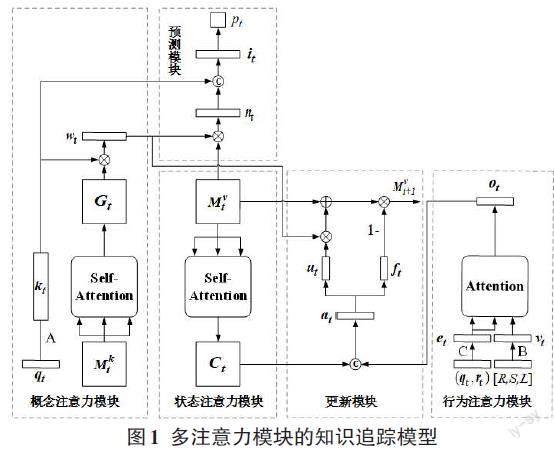
文章提出了多注意力模块的知识追踪模型（Knowledge Tracing Model Base on Attention Mechanism，AMKT），其整体结构如图1所示。

3.1 概念注意力模块

将存储概念的矩阵[Mkt∈?dk×N]作为模块中自注意力机制的输入，用来计算概念间的相似性，计算结果用概念注意力矩阵[Gt]表示。受文献[10]的启发，模型采用缩放点积自注意力机制：

[Gt=Softmax（MktMkTtdk）Mkt] （1）

为了得到习题[qt]中所含概念间的相似性，将习题[qt]转换成one-hot编码，再与嵌入矩阵[A∈?dk×N]相乘得到习题嵌入向量[kt]。[kt]与[Gt]相乘通过[Softmax]函数轉化为关联权重[wt]，表示习题[qt]所含概念间的相似性。

[wt=Softmax（kt×Gt）] （2）

3.2 状态注意力模块

将存储概念掌握状态的矩阵[Mvt∈?dv×N]作为模块中自注意力机制的输入，用来计算概念掌握状态间的相似性，计算结果用状态注意力矩阵[Ct]表示。

[Ct=Softmax（MvtMvTtdv）Mvt] （3）

3.3 行为注意力模块

在行为注意力模块中，首先将遗忘因素拼接组成一个维度为3的行向量[[R，S，L]]并执行归一化操作，再将其与嵌入矩阵[C∈?3×dv]相乘得到一个维度为[dv]向量[vt]，表示学生在学习过程中的行为。[E]是学生的习题交互[（qt，rt）]，将其转换成one-hot编码并与嵌入矩阵[B∈?dv×2N]相乘，得到维度为[dv]的向量[et]，表示[t]时刻学生的习题交互[（qt，rt）]。

使用注意力机制来发掘两者间的联系，将表示自主性提示的向量[vt]作为注意力机制中查询的输入，将表示非自主性提示的向量[et]作为注意力机制中键和值的输入：

[ot=Softmax（vtetT）et]    （4）

行为注意力向量[ot]是行为注意力模块中注意力机制的计算结果，其维度为[dv]，是对向量[vt]和[et]的综合表示。

3.4 更新模块

行为注意力向量[ot]和状态注意力矩阵[Ct]是建模学习行为和遗忘行为的重要因素，将两者拼接并输入至一层带有[Tanh]激活函数的全连接层，得到一个维度为[dv]的列向量[at]，是向量[ot]和矩阵[Ct]的综合表示。

[at=Tanh（wT1[Ct，ot]+b1）] （5）

利用一层带有 [Sigmoid]激活函数的全连接层将向量[at]转换成遗忘向量[ft]：

[ft=Sigmoid（WTfat+bf）] （6）

其中，全连接层的权重矩阵[Wf]的形状是[dv×dv]，偏置向量[bf]的维度是[dv]。遗忘向量[ft]是一个[dv]维的列向量，是对学生[t]时刻遗忘行为建模的结果。

利用一层带有[Tanh]激活函数的全连接层将向量[at]转换为学习向量[ut]：

[ut=Tanh（WTuat+bu）] （7）

其中，全连接层的权重矩阵[Wu]的形状是[dv×dv]，偏置向量[bu]的维度是[dv]。学习向量[ut]是一个[dv]维的列向量，是对学生[t]时刻学习行为建模的结果。

学习向量[ut]和遗忘向量[ft]以及关联权重[wt]用于下一时刻的矩阵[Mvt+1]的更新：

[Mvt+1（i）=Mvt（i）（1-ft）+utwt（i）] （8）

3.5 预测模块

在预测模块中，将关联权重[wt]与矩阵[Mvt]相乘，得到向量[nt]，是学生概念掌握状态的输出：

[nt=wtMvt] （9）

考虑到习题间会存在一定的差异，如难度系数不同，将向量[nt]与习题嵌入向量[kt]进行拼接，这样得到的向量既包含了學生的概念掌握状态又包含了习题信息，将这个向量输入至带[Tanh]激活函数的全连接层，得到向量[it]：

[it=Tanh（wT2[nt，kt]+b2）] （10）

最后，利用一个带有[Sigmoid]激活函数的输出层，将[it]作为输入，用来预测学生对习题[qt]的表现情况：

[pt=Sigmoid（wT3it+b3）] （11）

3.6 AMKT模型应用

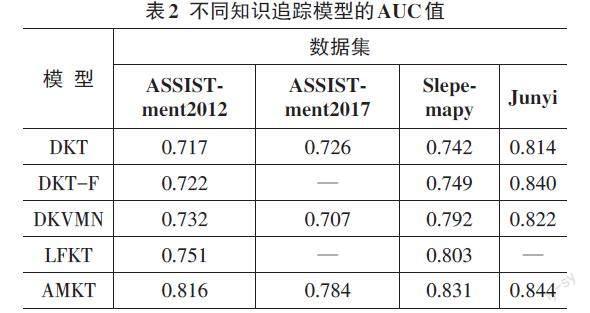
文章使用AUC（Area Under Curve）和ACC（Accuracy Rate）作为模型的评价指标，在知识追踪领域中，AUC被普遍选为评价指标，若AUC的值为0.5，说明模型是随机预测模型；AUC的值越大，说明模型预测性能越好。文章选择DKT、DKVMN、DKT-F以及LFKT作为对比模型，验证AMKT模型的性能。实验结果如表2所示，表中“—”表示无法获取模型在数据集下的实验结果。

从实验结果可以看出，AMKT模型在四个数据集上的AUC、ACC值均超过了其他模型，AUC值分别达到了0.816，0.784，0.831，0.844，验证了AMKT的有效性。

在英语课程教学中选出2个班的学生，班级1作为对照组，正常开展教学活动；班级2作为实验组，使用AMKT模型辅助开展教学活动。统计每位学生的最终作业或测验的完成情况，若某生的作业或测验成绩达到或超过“良好”，则认为该生已经掌握了相关概念，否则认为该生未掌握相关概念。表3展示了两个班的掌握率情况。

从实验结果可以看出，两个班的初始掌握率差别不大，但班级2使用AMKT模型辅助教学后其最终掌握率要高于班级1。这表明知识追踪模型衡量学生知识状态，为智慧教育模式提供支撑是有效的。

4 结论

随着科学技术的不断发展，信息、知识大爆炸时代已经来临，教育信息化是未来教育发展的趋势之一。虽然教育信息化能够在一定程度上缓解传统教育模式存在的限制，但教育信息化自身也存在诸多缺陷，例如老师精力有限，难以为每个学生提供细粒度的教育服务；教育资源丰富多样，学生难以快速选择适合自己的教育资源等。智慧教育模式是解决这些问题的选择之一，在智慧教育中，知识追踪为细粒度教育服务提供知识状态的支撑。文章提出了基于注意力机制的知识追踪模型（AMKT），对学习和遗忘行为进行建模。在四个真实数据集上和多个知识追踪模型进行了性能对比实验，并将AMKT应用于英语课程辅助教学中。结果表明， AMKT模型在性能上要优于其他模型，且知识追踪模型衡量学生知识状态，为智慧教育模式提供支撑是有效的。

参考文献：

[1] Bakhshinategh B，Zaiane O R，Elatia S，et al.Educational data mining applications and tasks： a survey of the last 10 years[J].Education and Information Technologies，2018（23）：537-553.

[2] 曾凡智，许露倩，周燕，等.面向智慧教育的知识追踪模型研究综述[J].计算机科学与探索，2022，16（8）：1742-1763.

[3] 卢宇，王德亮，章志，等.智能导学系统中的知识追踪建模综述[J].现代教育技术，2021，31（11）：87-95.

[4] 梁琨，任依梦，尚余虎，等.深度学习驱动的知识追踪研究进展综述[J].计算机工程与应用，2021，57（21）：41-58.

[5] Corbett A T，Anderson J R.Knowledge tracing： Modeling the acquisition of procedural knowledge[J].User modeling and user-adapted interaction，1994，4（4）：253-278.

[6] Piech C， Spencer J， Huang J， et al. Deep Knowledge Tracing[J]. Computer Science， 2015，3（3）：19-23.

[7] Zhang J，Shi X，King I， Yeung， D. Y.Dynamic key-value memory networks for knowledge tracing[C].Proceedings of the 26th international conference on World Wide Web，2017：765-774.

[8] Nagatani K，Zhang Q，Sato M，et al.Augmenting knowledge tracing by considering forgetting behavior[C].The world wide web conference，2019：3101-3107.

[9] 李晓光，魏思齐，张昕，等.LFKT： 学习与遗忘融合的深度知识追踪模型[J].软件学报， 2021，32（3）：818-830.

[10] Vaswani A，Shazeer N，Parmar N，et al.Attention is all you need [C].Proceedings of the 31st International Conference on Neural Information Processing Systems，2017：6000-6010.

【通联编辑：王力】