基于SVM的双辅助永磁体Halbach阵列潜油永磁同步电机优化设计

刘广孚, 于建宗, 郭 亮, 宁 波

(1.中国石油大学(华东)控制科学与工程学院,山东青岛 266580; 2.中国石油大学(华东)海洋与空间信息学院,山东青岛 266580; 3.广州海洋地质调查局,广东广州 511458)

随着稀土资源的开发与永磁材料加工技术的进步,具有高功率密度,高效率等优点的潜油永磁同步电机(submersible permanent magnet synchronous motor)已广泛应用于油田。近年来高性能永磁材料钕铁硼的出现大大促进了潜油永磁电机的发展。气隙磁密波形的正弦度对电机输出转矩、反电动势波形、铁心损耗和电磁噪声具有很大的影响,气隙磁密的谐波含量高,会使电机的振动与噪声较大,同时谐波感应电势与谐波电流还会导致谐波损耗增加,降低了电机的运行效率[1]。因此如何提升潜油永磁电机气隙磁密的正弦度、降低气隙磁密的谐波畸变率一直是潜油电机优化设计研究的重点。Xu等[2-4]提出了一种两级Halbach结构的电机,这种电机有较好的气隙磁密正弦度和较低的转矩脉动。Jian等[5-6]提出了一种三段式的Halbach阵列磁极结构并且通过实验证明了该种结构在优化磁密方面的有效性,但是没有对提出的结构进行进一步的优化。高锋阳等[7]提出了一种不等宽不等厚的Halbach阵列模型,来提升电机性能,采用解析法分析电机,在优化时没有考虑边界磁极结构的多样性。目前结构参数组合优化主要分为数学解析法[8-9]、有限元电磁分析法[10-11],解析法建立的数学表达式用于定量计算,精度不高[12]。有限元法需要进行大量有限元建模前期预处理和计算,计算成本巨大,计算效率低。潜油永磁同步电机的多目标优化方法有很多种,Guo等[13-16]提出了一种基于模糊田口法的优化方法解决多目标优化问题,该方法能够在更优的目标函数中获得更好的性能特性。Mirnikjoo等[17]通过TOPSIS的决策算法解决多目标优化设计中结果评估时的目标之间互相冲突的问题[18]。笔者提出一种新型的双辅助永磁体Halbach阵列结构来提升潜油永磁同步电机的气隙磁通密度基波幅值和降低潜油永磁同步电机的气隙磁通密度波形的畸变率。为了对电机进一步优化,笔者基于支持向量机建立电机径向气隙磁场的非参数模型,引入转动惯量,设计三变量三目标的多目标优化方案,通过权重系数法和优劣解距离法(technique for order preference by similarity to an ideal solution,TOPSIS)选定最优结果。

1 结构模型和谐波分析

1.1 结构模型

对一台18槽16极的50 kW表贴式潜油永磁同步电机进行优化,电机单节(5 kW)的基本参数:转子外径为99 mm,定子内、外径分别为100.5和155 mm,转子极对数为8,定子槽数为18,永磁体厚度为6 mm,电机长度为678.5 mm。为达到优化目标,在不等宽不等厚的单辅助永磁体Halbach阵列的基础上,提出双辅助永磁体Halbach阵列,如图1(图中,h为辅助永磁体厚度,θ为辅助永磁体Ⅱ充磁角)所示。从图1中可以看出,每个磁极都由一块主磁体和两种辅助磁体组成,主磁体为径向充磁,辅助磁体为不同方向的平行充磁。其中辅助磁体Ⅰ沿着转子圆周充磁,辅助磁体Ⅱ的充磁角为偏主永磁体方向的45°,辅助磁体与主磁体不等宽且不等厚。

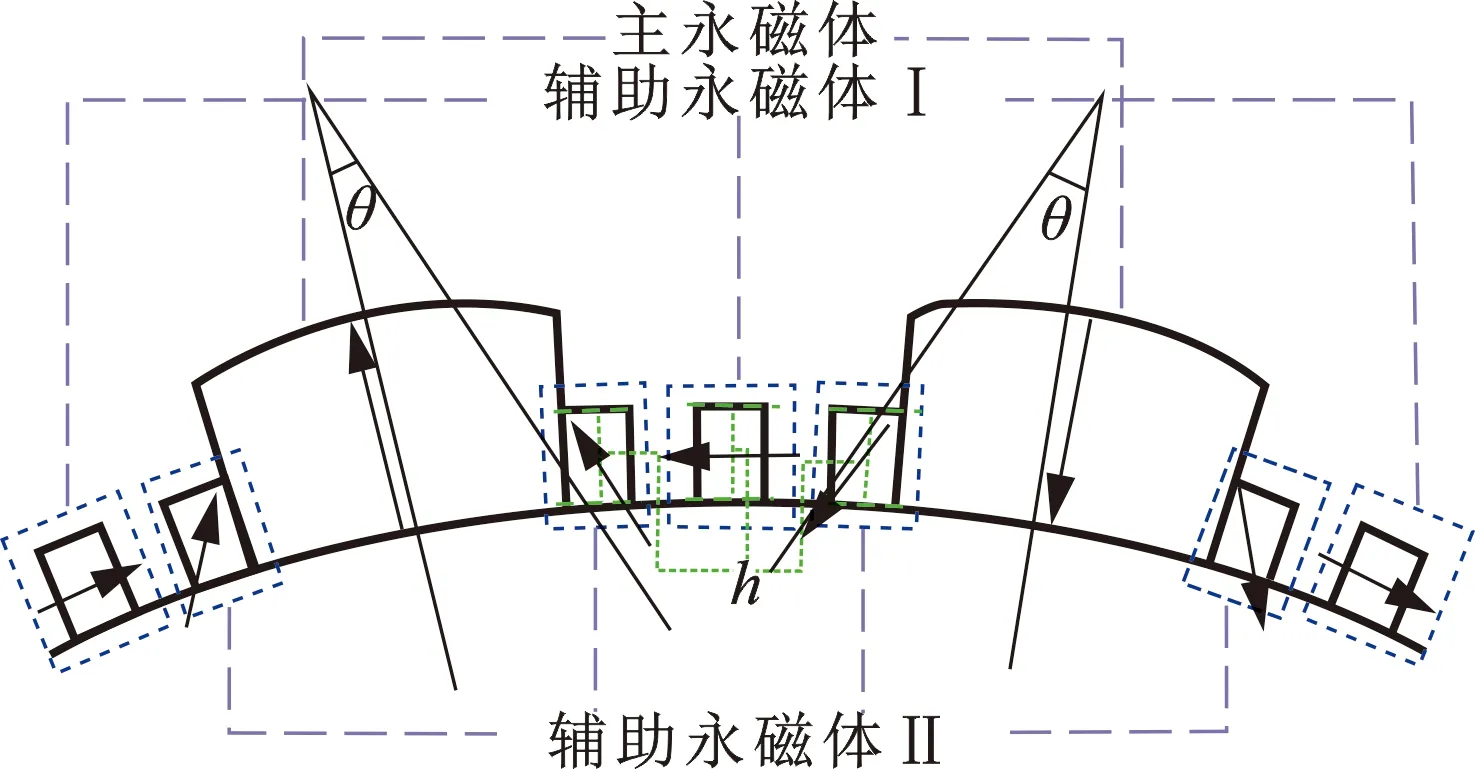
图1 永磁体结构示意图Fig.1 Schematic diagram of permanent magnet structure

为了使相互比较的电机模型永磁体用量相等,调整原始电机的永磁体量。基于有限元方法建立3种结构的电机模型,如图2所示。其中图2(b)、 (c)、 (d)的永磁体用量相等。

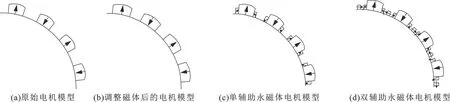
图2 电机有限元结构模型Fig.2 Finite element structural model of motor

基于图2中的有限元结构模型,永磁体、气隙、绕组满足自然边界条件,最外边界区域满足第一类齐次边界条件。电机转速设定为300 r/min(额定转速),则4种电机的磁通如图3所示。

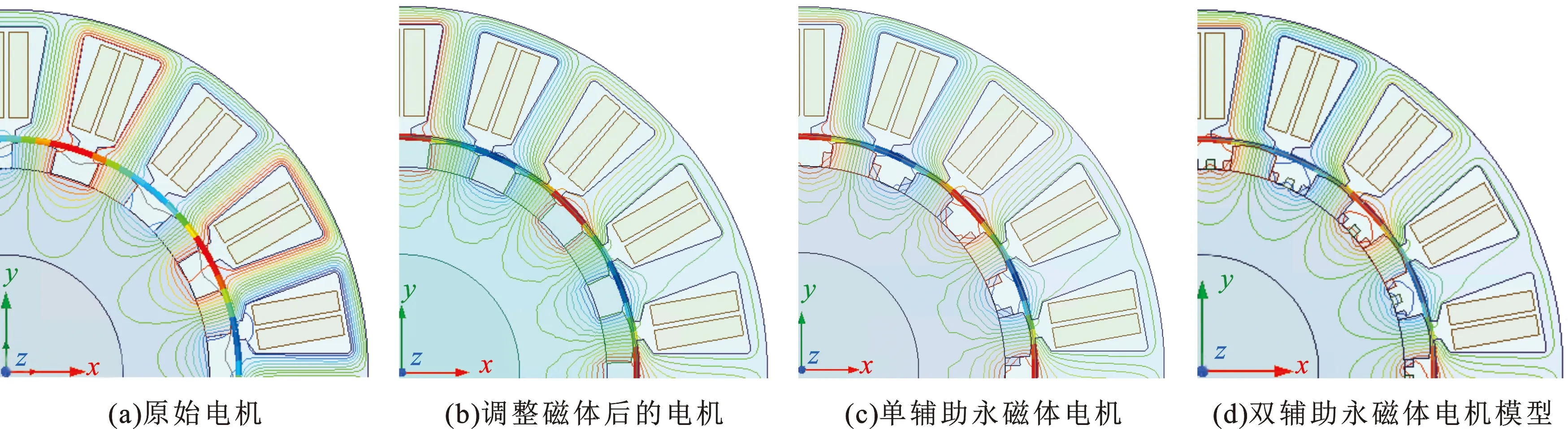
图3 电机有限元计算结果Fig.3 Finite element calculation results of motor

由于不同路径的气隙沿圆周径向气隙磁密变化趋势一致,取气隙中心一周的径向气隙磁密为对象展开研究。为了便于观察,取其中一个波峰进行对比。4种结构的径向气隙磁密曲线对比如图4所示。

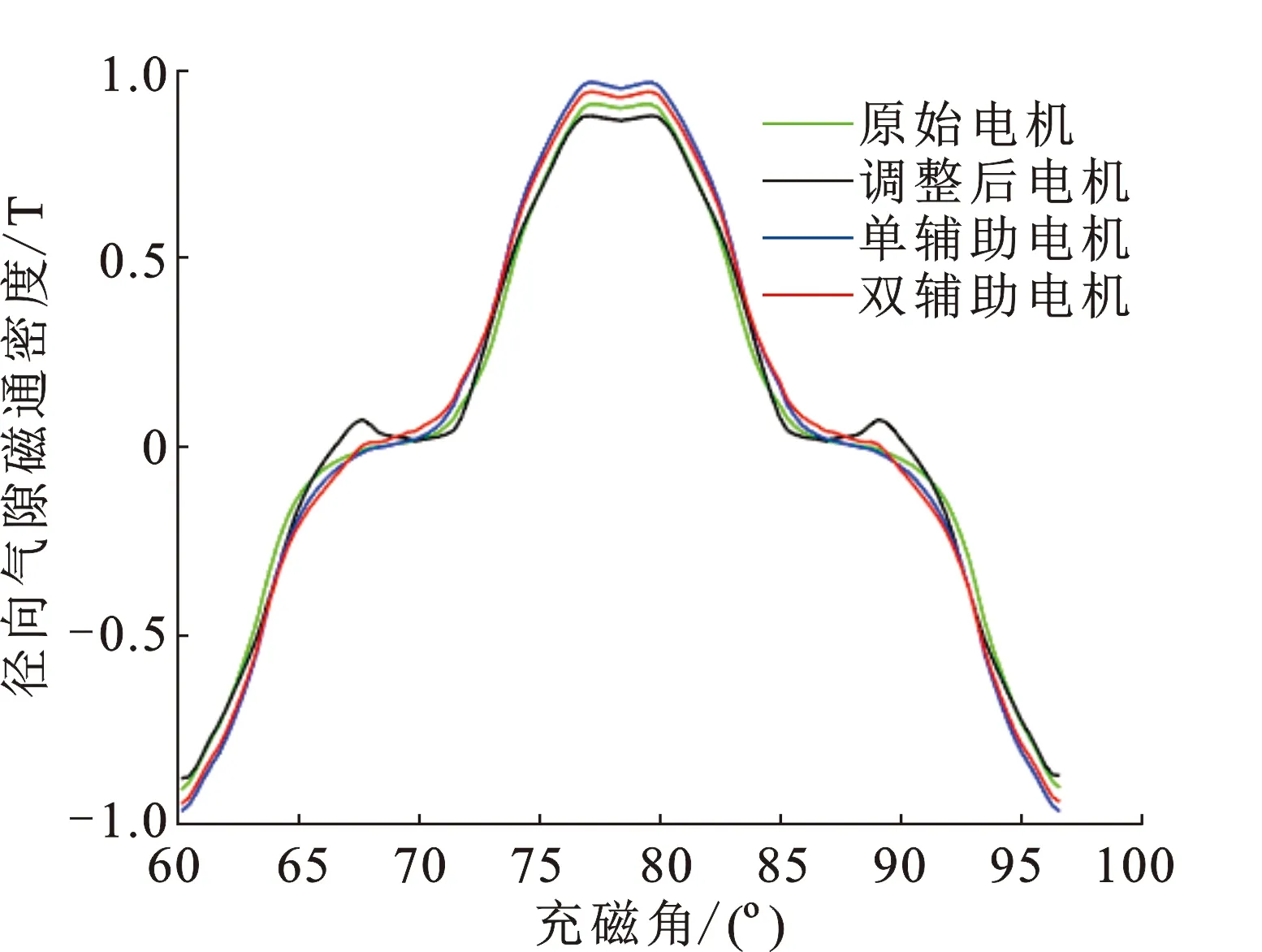
图4 电机径向气隙磁密对比Fig.4 Comparison of radial air gap magnetic density of motor

对径向气隙磁密进行傅里叶变换得到气隙磁密的基波和高次谐波。为了定量衡量谐波,定义波形畸变率DTH为

(1)

式中,n为谐波次数;G1为基波分量有效值;Gn为各谐波分量有效值。

图5给出了不同结构下的径向气隙磁密的波形畸变率和基波幅值对比结果。由图5可以看出,双辅助永磁体Halbach阵列结构电机的DTH和基波幅值分别为0.2848和0.7993 T,优于原始电机的0.36、0.724 T,也优于调整磁体后电机的0.3362和0.7539 T和单辅助永磁体Halbach阵列结构电机的0.3082和0.7936 T。这说明双辅助永磁通Halbach阵列电机拥有更小的气隙磁密谐波畸变率和更大的气隙磁密基波幅值,电机的气隙磁密的优化效果明显。

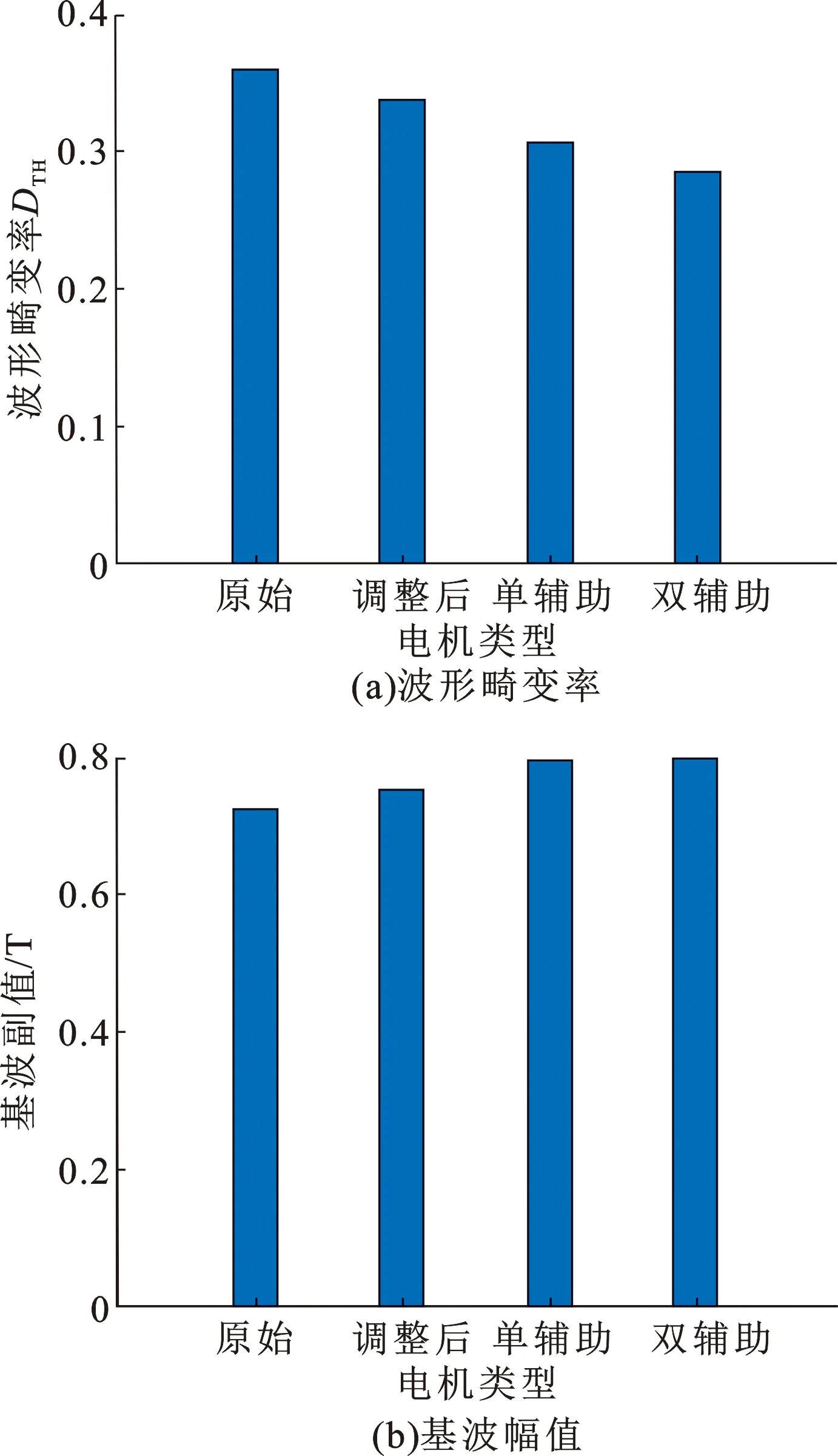
图5 波形畸变率和基波幅值对比Fig.5 Comparison of waveform distortion rate and fundamental amplitude

1.2 谐波分析

在双辅助永磁体Halbach阵列结构电机中,不同的结构参数对径向气隙磁密的波形畸变率和基波幅值的影响不同。选取双辅助永磁体厚度、辅助永磁体Ⅱ的充磁角、气隙长度为优化对象,对电机的单个参数分别进行谐波分析。

由于主永磁体的厚度为6 mm,双辅助永磁体厚度为1～6 mm,其他参数保持不变。图6为波形畸变率和基波幅值的变化趋势。由图6(a)可知,径向气隙磁密的波形畸变率随着辅助永磁体Ⅰ和Ⅱ厚度的增大而减小,基波幅值随着辅助永磁体Ⅰ和Ⅱ厚度的增大而增大。为了便于建立正交表,在正交表中选择1～3.5 mm,这个取值范围可以满足支持向量机模型的训练。

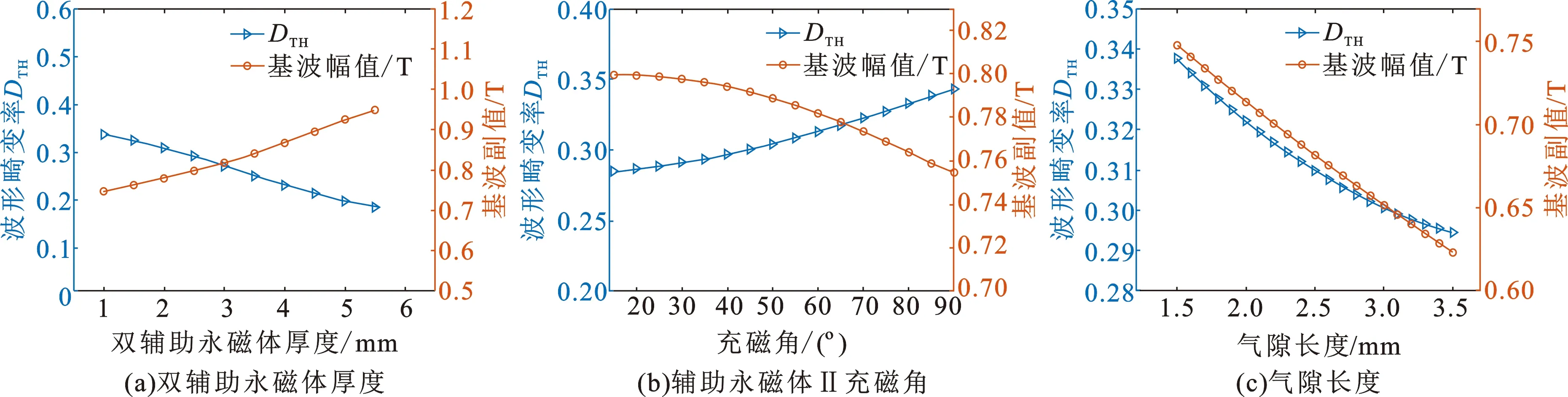
图6 波形畸变率和基波幅值的变化趋势Fig.6 Variation trend of waveform distortion rate and fundamental wave

辅助永磁体Ⅱ充磁角取为0°～90°,其他参数保持不变。由图6(b)可知,径向气隙磁密的波形畸变率随着辅助永磁体Ⅱ充磁角的增大而增大,且趋势越来越陡峭;基波幅值随着辅助永磁体Ⅱ充磁角的增大而减小,且趋势越来越陡峭。

气隙长度的取值范围为1～3.5 mm,其他参数保持不变。由图6(c)可知,径向气隙磁密的波形畸变率和基波幅值都随着气隙长度的增加而减小,且趋势逐渐放缓。考虑到实际工程中的需要,取值范围选为1.5～2.5 mm。

2 转动惯量的计算和SVM建模

潜油永磁同步电机的转动惯量也是影响其性能的重要因素。为了尽量减小转动惯量,引入转动惯量作为优化目标之一。

2.1 转动惯量计算

转动惯量为

(2)

式中,J为刚体的转动惯量,kg·m2;Δmi为质点质量,kg;ri为质点到转轴的距离,m。

表贴式潜油永磁同步电机转子分为永磁体和铁心两部分。由于两部分的材料、形状都不相同,所以转动惯量的计算公式也不一样。为了简化计算,将永磁体部分简化为扇环体。根据式(2)可得单块主永磁体的转动惯量为

(3)

式中,J1为单块主永磁体的转动惯量,kg·m2;Ro和Ri分别为扇环的外径和内径,m;ρp为永磁体密度,取为7 550 kg/m3;hr为电机长度,取为685.5 mm;θr为扇环对应的圆心角,取为11.25°。

单块辅助永磁体的转动惯量表达式与式(3)相同,Ro、Ri、θr取辅助永磁体对应的值,单块辅助永磁体的转动惯量用J2表示。

转子铁心的转动惯量为

(4)

式中,J3为转子铁心的转动惯量,kg·m2;ρi为铁心密度,取为7 372 kg/m3。

双辅助永磁体Halbach阵列潜油永磁同步电机以z轴为转轴时的转动惯量Jz为

Jz=J1+J2+J3.

(5)

2.2 SVM回归算法

支持向量机是将非线性函数关系映射为高维空间的线性问题,再在这个高维空间中寻求最优回归超平面,使得所有样本离该最优超平面的距离最小,从而完成样本训练和数据回归[19-20]。超平面f(x)为

f(x)=ωTφ(xi)+b.

(6)

式中,ω为权重;φ(xi)为映射函数;b为偏置项。

假设线性回归函数可以在精度ε下拟合样本空间数据,则

(7)

最优回归超平面转化为二次规划问题为

(8)

约束条件为

(9)

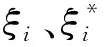
利用Lagrange优化方法将其转化为对偶形式,最终得到回归函数f(x,a)为

(10)

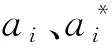
约束条件为

(11)

选泛化能力好的RBF径向基核函数,其公式为

(12)

式中,δ为函数的宽度参数,控制了函数的径向作用范围。

2.3 SVM回归建模

支持向量机建模之前需要一定数量的数据作为训练集和测试集,因此需要建立合适的样本空间数据。

对双辅助永磁体厚度、辅助永磁体Ⅱ充磁角,气隙长度进行优化,其样本空间如表1所示。

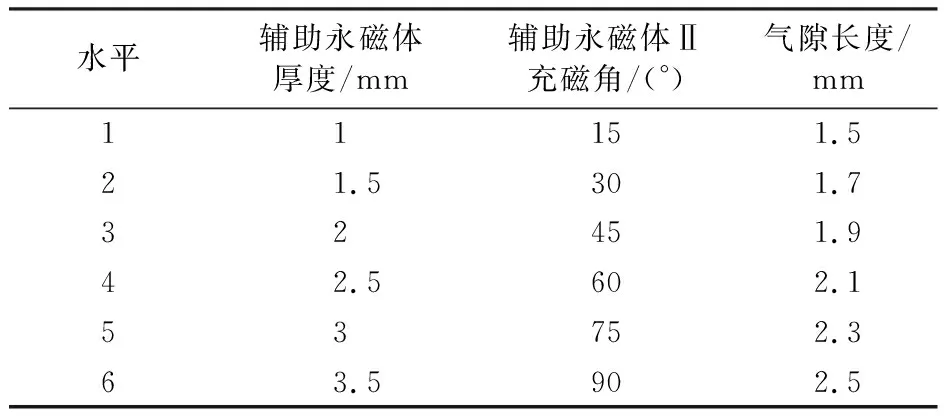
表1 样本空间Table 1 Sample space

正交实验可以对多因素水平进行优化设计,具有均匀统一的特点,能够在很大程度上减少实验次数,节约实验成本。正交表是正交实验的关键,根据表1所示的样本空间,选择6水平3因素的正交表。L40(63)正交表选择该数据集的80%作为支持向量机的训练集,20%作为支持向量机的测试集。

支持向量机的惩罚因子C和核参数δ是其性能的主要性能参数。惩罚因子C的作用是衡量其对误差的容忍度,核参数δ的改变会影响映射函数,从而改变样本在高维特征空间上的分布。用均方误差(EMS)来衡量支持向量机回归模型的精度,其表达式为

(13)

式中,fFEM为通过有限元计算得到的目标值;fSVM为通过支持向量机得到的目标值。

图7给出了通过网格搜索算法对参数C、δ的寻优过程,最终得到波形畸变率的最优参数分别为C=3.249,δ=0.1436;基波复制的最优参数分别为C=955.426,δ=0.0039。波形畸变率和基波幅值对应的均方误差分别为0.1228%和0.16419%。图8为基于该参数的的支持向量机模型和有限元模型在训练集和测试集上的对比结果。由图8可知,虽然有些点的有限元数据与支持向量机数据存在误差,但是二者的趋势基本一致,这说明该参数对应的支持向量机模型的拟合效果较好。

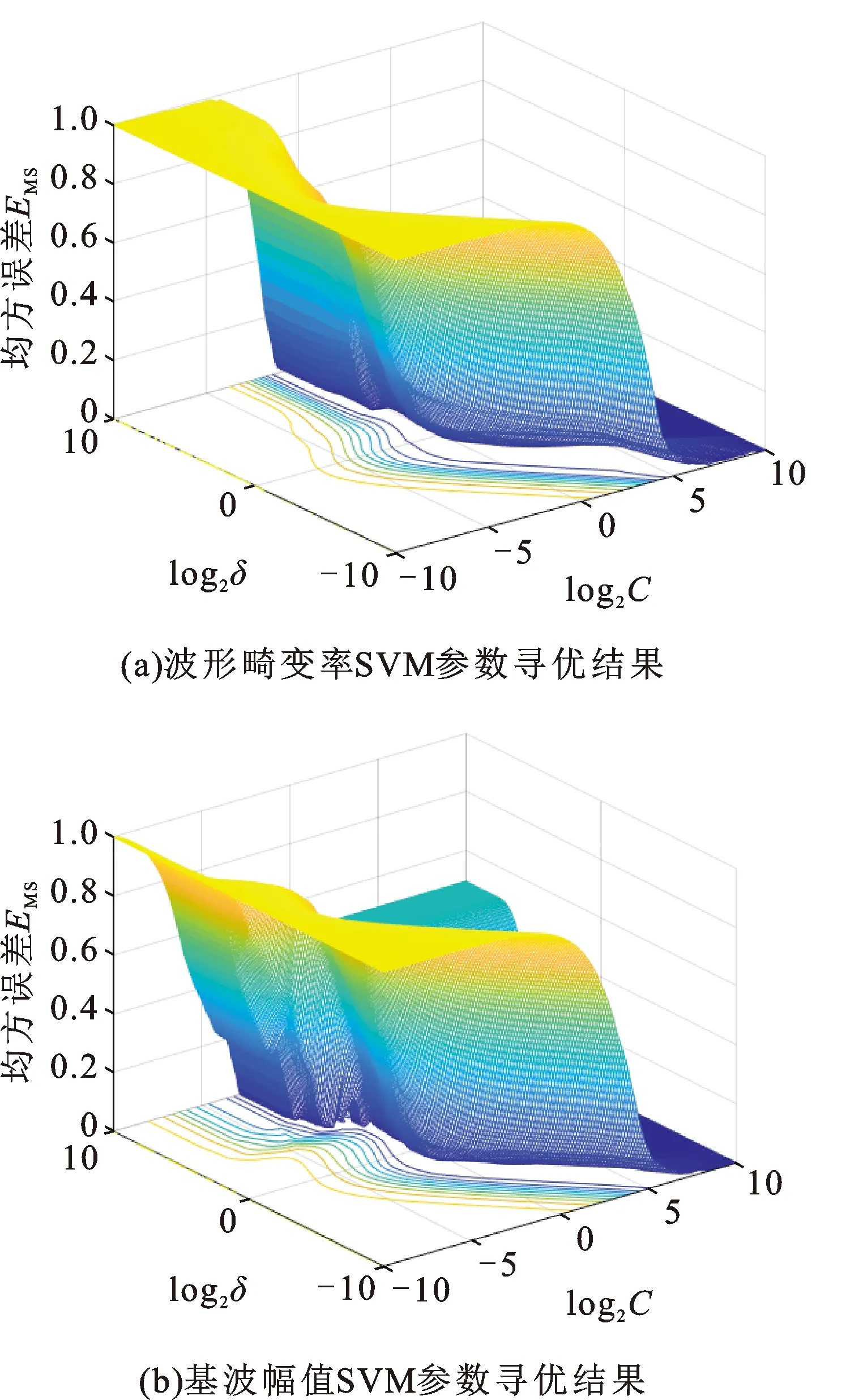
图7 参数寻优结果Fig.7 Parameter optimization results

3 多目标优化

3.1 多目标设计

选取电机径向磁密的波形畸变率、基波幅值和电机的转动惯量作为目标进行优化。对于多目标优化问题,由于各目标之间相互冲突,很难找到一个最优解,通过给不同的目标加上不同的权重从而将多目标问题转化为单目标优化问题。目标函数为

(14)

其中

式中,T1、T2为波形畸变率和基波幅值的参考值;K1、K2、K3分别为波形畸变率、基波幅值、转动惯量对应的权重;t1、t2分别为波形畸变率和基波幅值的计算值;t3为转动惯量的归一化值;JZ为当前电机的转动惯量,kg·m2;Jmax和Jmin分别为正交表中的参数对应的转动惯量最大值和最小值。

3.2 多目标决策

在对目标进行寻优过程中,式(14)权重的不同会导致寻优结果不同,权重的配比需要由实际情况确定。

以0.1的步长生成了36组不同的权重配比,即有36种优化方案。计算每种方案下的多目标优化结果,不同的权重系数及其优化结果如表2所示。

表2 不同权重系数的优化结果Table 2 Optimization results of different weight coefficients

表2所展示的波形畸变率、基波幅值和转动惯量都是归一化结果,对于不同的可行解,通过优劣解距离法(TOPSIS)筛选出最优解。

TOPSIS是根据有限个评价对象与理想化目标的接近程度进行排序的方法[21-22]。因为不同目标的最优指标不同,所以在TOPSIS中首先要将矩阵正向化,将目标变为相同指标。正向化矩阵为

(15)

式中,u为要评价对象的个数;v为评价的指标数。

(16)

通过式(17)对正则化矩阵X进行标准化,标准化后的矩阵为Z,表示为

(17)

定义Z的最大值为

Z+=(max{z11,z21,…,zu1},…,max{z1v,z2v,…,zuv}).

(18)

最小值为

Z-=(min{z11,z21,…,zu1},…,min{z1v,z2v,…,zuv}).

(19)

则其评价对象与最大值之间的距离为

(20)

评价对象与最小值之间的距离为

(21)

可得到其贴近度为

(22)

根据式(23)得到36组可行解的贴近度如图9所示。从图9中可以看出,第30组结果最优,贴合度为0.756,此时其权重系数K1、K2、K3分别为0.5、0.4、0.1,对应的辅助永磁体厚度、辅助永磁体Ⅱ充磁角、气隙长度的优化结果分别为4.63447 mm、13.2391°、1.8125 mm,最终取优化结果分别为4.6 mm、13.2°、1.8 mm。电机最终的结构如图10所示。

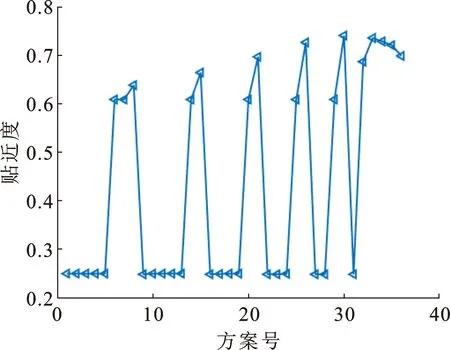
图9 各组优化结果的贴近度Fig.9 Closeness of optimization results of each group

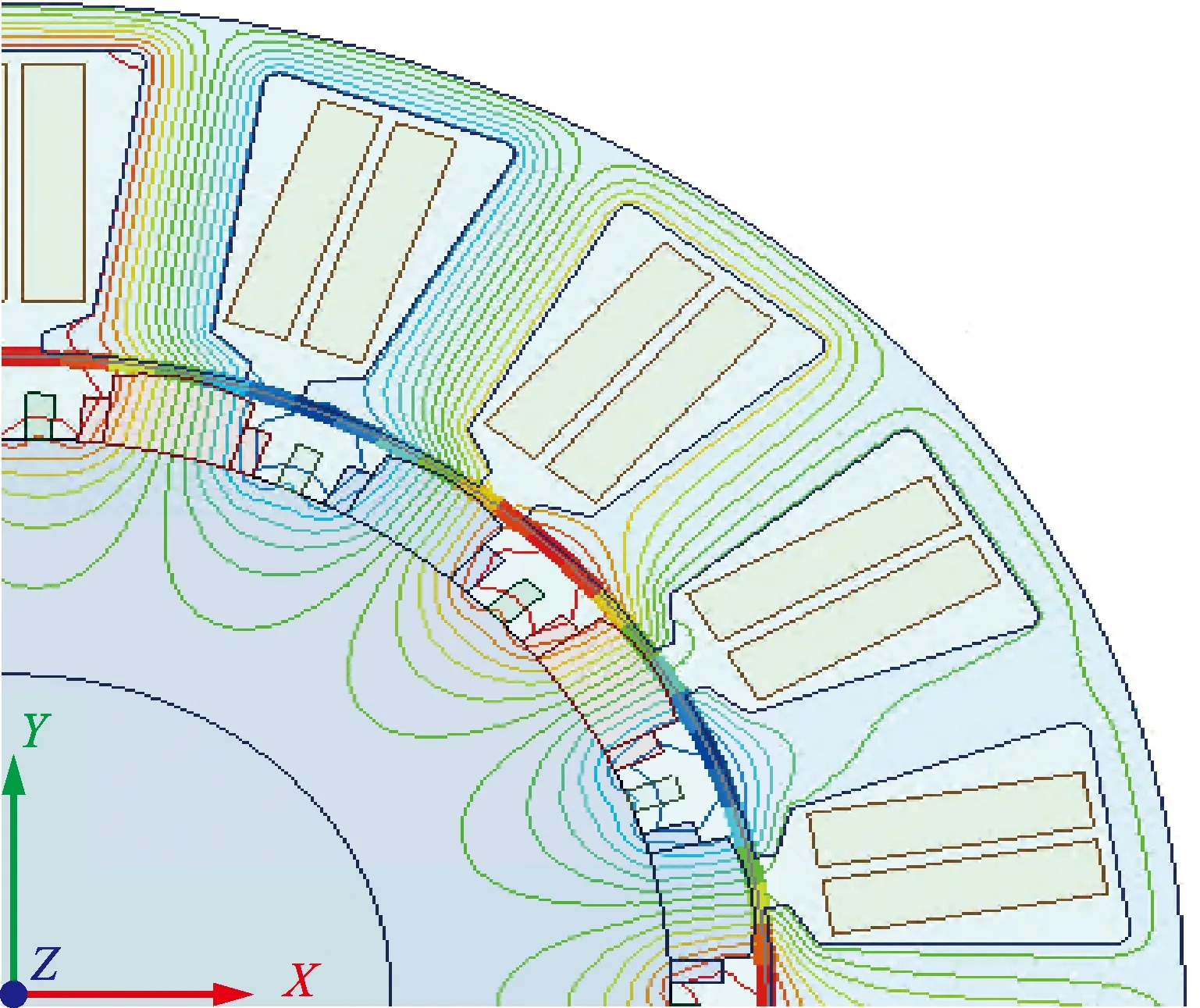
图10 优化后的最终结构Fig.10 Optimized final structure

3.3 仿真验证

18槽16极潜油永磁同步电机的原始电机参数与双辅助永磁体Halbach阵列寻优前后的参数对比如表3所示。

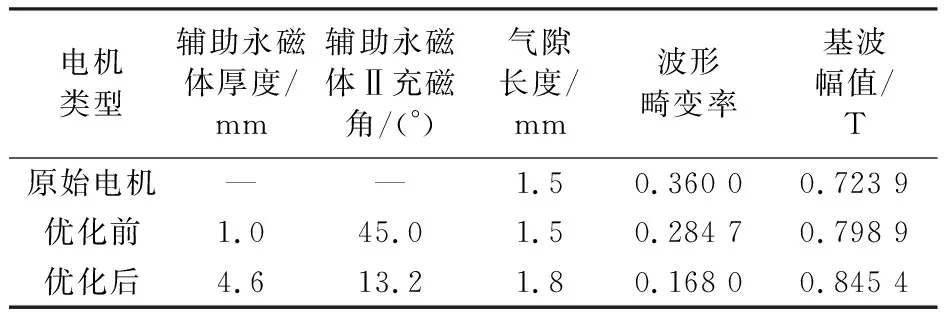
表3 电机参数对比Table 3 Comparison of motor parameters

电机优化前后的空载反电动势波形和径向气隙磁密波形对比如图11、12所示。可以看出优化后的空载反电动势和气隙磁密的基波幅值和正弦度都要优于原始电机和优化前的双辅助Halbach电机。

从图11、12中可以看出,双辅助Halbach结构显著降低了潜油永磁同步电机径向气隙磁密的波形畸变程度,并且提高了其基波幅值。优化后的双辅助永磁体Halbach阵列潜油永磁同步电机的波形畸变率为0.168,较原电机降低了53.3%;基波幅值为0.845 4 T,较原电机提升了16.8%。图13为优化前后的永磁体涡流损耗对比,原始电机的平均涡流损耗为4.03 W,优化前、后电机的平均涡流损耗分别为4.93 和8.67 W。这是因为双辅助永磁体Halbach阵列改变了永磁体结构,且优化后永磁体用量变多导致的。虽然涡流损耗变大,对于单节功率为5 kW的潜油电机来讲,仅增加了4.64 W的永磁体涡流损耗,不到电机功率的0.1%,但是气隙磁密大为改善。

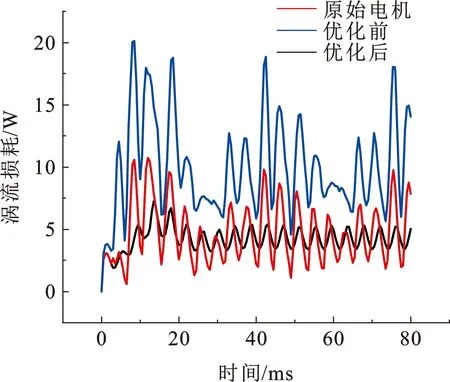
图13优化前后的永磁体涡流损耗对比Fig.13 Comparison of eddy current loss of permanent magnet before and after optimization

4 结 论

(1)双辅助Halbach阵列由主永磁体和两种辅助永磁体构成,该结构有更小的径向气隙磁密的波形畸变率和更大的基波幅值。

(2)优化后的双辅助永磁体Halbach阵列潜油永磁同步电机的波形畸变率为0.168,较原电机降低了53.3%;基波幅值为0.845 4 T,较原电机提升了16.8%,提出的双辅助Halbach电机可大大改善潜油永磁同步电机径向气隙磁密的正弦度,提升电机性能。