基于简化开关函数的电网换相换流器直流侧简化阻抗建模方法

李永琪，陈代忠，王顺亮，马俊鹏，彭茂兰，冯 雷，刘 航

（1.四川大学电气工程学院，四川成都 610065；2.中国南方电网有限责任公司超高压输电公司，广东广州 510663）

0 引言

现今基于电网换相换流器（Line Commutated Converter，LCC）的传统高压直流（High Voltage Direct Current，HVDC）输电系统技术已非常成熟[1-4]，被广泛应用于实际工程。由于LCC 具有价格较低的优势，未来仍有很长一段时间将继续服务于工程，尤其是大型多端混合直流输电系统，将LCC 作为整流侧以避免发生换相失败[5-10]。但LCC 在运行过程之中会产生大量谐波，在与外部系统相连时，若存在谐波阻抗较小并趋近于0 的情况，将导致严重的谐波放大，危害系统的安全运行[11-13]。目前交流滤波技术已经非常成熟，而直流滤波技术还有待提升，因而有必要研究LCC 直流侧谐波阻抗特性，以避免发生直流侧谐波不稳定。

国内外相关研究中，文献[14]分析了兴安高压直流工程在遭受雷击后出现的直流125 Hz 谐振，基于实时数学物理闭环仿真平台复现了现场振荡现象。文献[15-17]采用频率扫描的方法获得了LCC的阻抗曲线，该方法虽然能够得到较准确的谐波阻抗曲线，但存在扫频耗时长的缺点，且LCC 系统中有任意参数的改变都需要重新进行频率扫描；文献[18-19]基于平均值法对LCC 建立等效谐波阻抗模型，将LCC 1 个周期内波动的电压电流用平均值代替，该方法简洁方便，但由于忽略了电压电流的波动导致谐波阻抗可用频带不高，只有300 Hz 左右；文献[20-21]使用开关函数法，认为直流电压和交流电流由交流三相电压和直流电流经开关函数调制而成，能够很好地解释交直流之间的谐波传递关系、计算LCC 阻抗，但该方法没有考虑LCC 换相过程，精度不高；文献[22-23]通过将换相电流近似线性上升/下降得到了考虑换相过程的LCC 小信号模型，精度得以提升；在此基础上，文献[24-25]进一步改善开关函数模型，用正弦曲线近似换相电流上升和下降过程提升LCC 阻抗建模精度，但精度提升的同时带来计算量大、计算过程复杂等不足。当实际工程发生谐波不稳定事件时，希望能够快速建立系统的阻抗模型并进行稳定性分析，及时提取振荡频率以采取合适的措施抑制谐波不稳定，因此需要一种简化的LCC 建模方法，在不失精度的条件下提高LCC 阻抗的计算速度。

本文通过对LCC 换相过程进行推导，提出了一种LCC 简化开关函数模型，将电压开关函数和电流开关函数统一，降低了一半的计算量，有效提升计算速度；再基于动态相量法，通过LCC 交、直流之间谐波传递的分析和计算，得到了LCC 直流侧简化阻抗表达式；最后通过在电磁暂态仿真软件PSCAD中搭建的模型验证了本文方法所得LCC 直流侧简化阻抗的正确性。

1 LCC简化开关函数

1.1 6脉动LCC结构

6 脉动LCC 结构如图1 所示。图1 中ua，ub，uc分别为交流三相电压，ia，ib，ic为交流三相电流，ud，id分别为LCC 直流侧电压、电流，Zd为直流侧负载等效阻抗，n0为负载中点，Lc为换流器变压器漏感，编号为T1-T6 的晶闸管依次导通，完成交直流之间的换流功能。

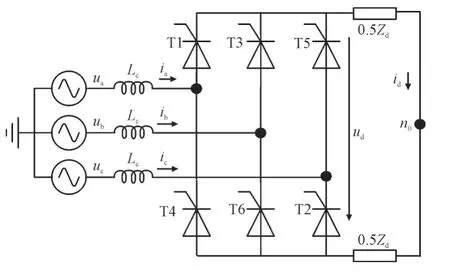
图1 6脉动LCC结构Fig.1 Structure of 6-pulse LCC

1.2 精确的LCC电压开关函数

根据开关函数模型，LCC 直流侧的电压可以表示为交流侧的电压经电压开关函数调制而成，交流侧的电流可以表示为直流侧的电流经电流开关函数调制而成，即：

式中：Sua，Sub，Suc分别为三相电压开关函数；Siϕ为ϕ相电流开关函数。

由于LCC 的关断需要外部电路提供反向压降，当下一个晶闸管导通时，需要关断的晶闸管会持续导通一段时间直到反压的到来，这段时间内会出现一极有2 个晶闸管同时导通的现象，该过程称为LCC 的换成重叠过程，如图2 所示。图2 中M为共阴极晶闸管和直流负载的连接点。

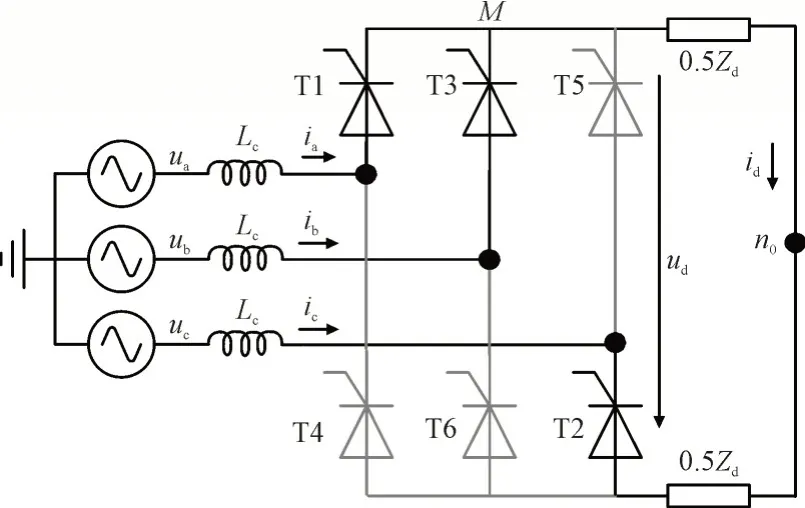
图2 LCC换相重叠过程Fig.2 Commutation overlap process of LCC

图2 为T1 向T3 换流的过程，T1 和T3 同时导通，根据电路结构，M点的电压uM满足：

A 相电流和B 相电流之和等于id，整理式（2），可得M点的电压表达式为：

此时直流侧电压ud的表达式为：

根据式（1）的开关函数模型，可得T1 到T3 换相过程中A，B 两相电压开关函数为0.5，C 相电压开关函数为-1。换相结束后T2 和T3 导通，ud=ubuc，A 相电压开关函数为0，B 相电压开关函数为1，C 相电压开关函数为-1。1 个周期内完整的A 相电压开关函数如图3 所示，其中a为触发角，ωt为相角，μ为换相重叠角，uac（bus）为母线电压，其表达式如式（5）所示，B 相和C 相的电压开关函数分别由A相滞后、超前120°得到。

图3 A相电压开关函数Fig.3 Phase A voltage switching function

1.3 简化的LCC开关函数模型

为了简化LCC 的开关函数模型，进一步分析换相过程中电压开关函数和电流开关函数的关系，图2 的等效电路如图4 所示。图4 中Ma和Mb分别为A 相和B 相晶闸管与直流负载的连接点，P为C 相晶闸管和直流负载的连接点。

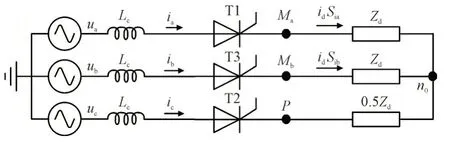
图4 LCC换相重叠过程等效电路Fig.4 Equivalent circuit of LCC commutation overlap process

根据图4，对应的电流开关函数关系为：

在换相过程中，A 相电流和B 相电流之和一直等于直流电流id，结合式（1）的电流开关函数模型，可得：

结合式（6）和式（7），电流开关函数和电压开关函数的关系为：

由式（7）可得，电流开关函数和电压开关函数相等，开关函数模型被统一，使用该模型使得LCC计算程序存储量降低一半，提高了计算的效率。

2 基于动态相量法的LCC直流侧简化阻抗

2.1 动态相量法

动态相量法以连续傅里叶变换为基础，对于一个连续时域信号x（t），在任意一个长度为T的时间区间t∈（τ-T，τ]，τ为时间变量，将其展开成傅里叶级数[26]：

n阶动态相量是关于τ的旋转变量，随着τ的改变而进行幅值和初相位的改变，其改变方式如图5 所示。图5 中Im 为虚部，Re 为实部，ω为角频率。

图5 动态相量示意图Fig.5 Schematic of dynamic phasors

当3 个时域信号m（t），v（t），p（t），满足m（t）=v（t）·p（t）时，则有：

式中：k为p（t）的动态相量阶数。

动态相量可由复数表示，以时域信号u（t）为例，它的±n次动态相量与n次谐波的对应关系为：

式中：U，φn分别为该信号的幅值和初相位。

±n次动态相量与n次谐波的幅值和初相位的具体关系为：

由式（13）可知，n次动态相量与-n次动态相量幅值均为0.5U，初相位相差一个负号。

2.2 LCC直流侧简化阻抗表达式

完整的LCC 系统如图6 所示，其中udLCC，idLCC分别表示LCC 直流侧电压和电流，uabc，iabc分别表示LCC 交流侧对应的三相电压和电流，Zs为交流系统阻抗，Zf为交流母线滤波器阻抗，kt为变压器变比，us为交流电压幅值。

图6 LCC系统示意图Fig.6 Schematic diagram of LCC system

由于6 脉动LCC 开关函数的谐波分量中，只有6k±1 次不为0，12 脉动LCC 开关函数的谐波分量重中只有12k±1 次不为0，且随着谐波次数的增加，谐波分量的值越小，因此忽略5 次及以上的谐波分量，将不会对计算结果产生太大的影响。

据此，本文将式（5）表示的统一电压电流开关函数代入式（10），转化为动态相量，然后取出开关函数动态相量的±1 次参与计算。

当图6 中直流侧电流idLCC有一个频率为f的扰动量ΔidLCC时，ΔidLCC（f）将通过电流开关函数的调制传递至交流侧，并在三相电流中产生频率为f±f0（f0为基波频率）的2 个电流扰动，即Δiabc（f+f0）和Δiabc（f-f0）。结合式（1）和式（11），可得Δiabc（f+f0）和Δiabc（f-f0）的计算式为：

Δiabc（f+f0）和Δiabc（f-f0）又分别会在ZAC（f+f0）和ZAC（f-f0）上产生电压扰动Δuabc（f+f0）和Δuabc（f-f0），其中ZAC为LCC 系统交流侧总的等值阻抗，其值等于交流系统阻抗Zs和交流滤波器阻抗ZF并联后折算到变压器低压侧的值：

Δuabc（f+f0）和Δuabc（f-f0）通过电压开关函数的调制又传递至直流侧产生直流电压扰动ΔudLCC：

最终根据直流侧的电压扰动和电流扰动，结合式（14）和式（15）得到频率为f时LCC 直流侧阻抗表达式：

考虑变压器漏感Lc对直流阻抗的影响，直流侧的电流扰动ΔidLCC（f）通过变压器漏感将在直流侧的压降为：

式中：μ0为换相重叠角的稳态值。

LCC 最终的直流侧阻抗表达式为：

式（19）同时含有电压和电流开关函数，在实际计算时计算量较大。因此将式（19）中的电压和电流开关函数用统一的简化开关函数式（5）替代，可得到LCC 直流侧简化阻抗表达式如式（20）所示。式（20）中Sϕ为ϕ相统一的简化开关函数，有Sϕ=Suϕ=Siϕ。

直流侧简化阻抗采用了统一的电压电流开关函数，使得计算量减小，且近似的电流开关函数可以描述换相过程中输出电流的变化，计算结果具有可靠性。

3 仿真验证

为了验证本文简化方法的正确性，在电磁暂态仿真软件PSCAD 中，搭建LCC 仿真模型，本文设置了3 种不同的LCC 仿真运行工况，分别为：

1）系统A：LCC 运行在逆变状态，定直流电压控制，系统电路如图7 所示，系统参数如表1 所示。图7 和表1 中Rs，Ls分别为交流系统电阻、电感，Cf1-Cf4，Lf1-Lf2，Rf1-Rf3分别为交流滤波器电容、电感和电阻参数，idcr为整流侧等效电流源，kpi，kii分别为定直流电压控制的PI 比例和积分参数，Gi，Ti分别为定直流电压控制的一阶滤波参数。

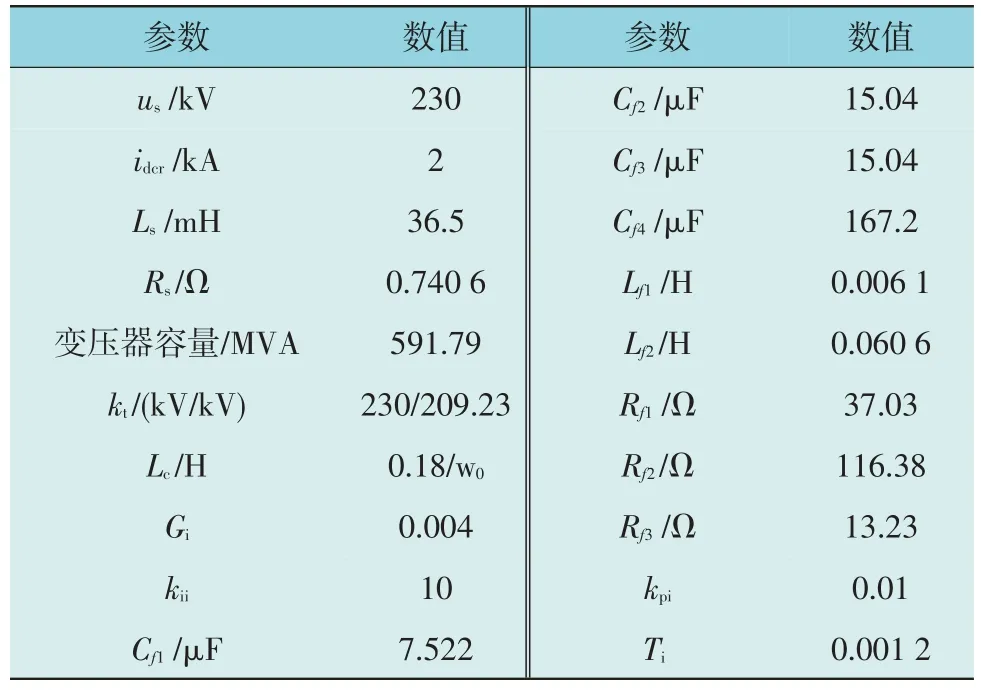
表1 逆变站LCC直流输电仿真系统参数Table 1 Parameters of inverter station LCC DC transmission simulation system

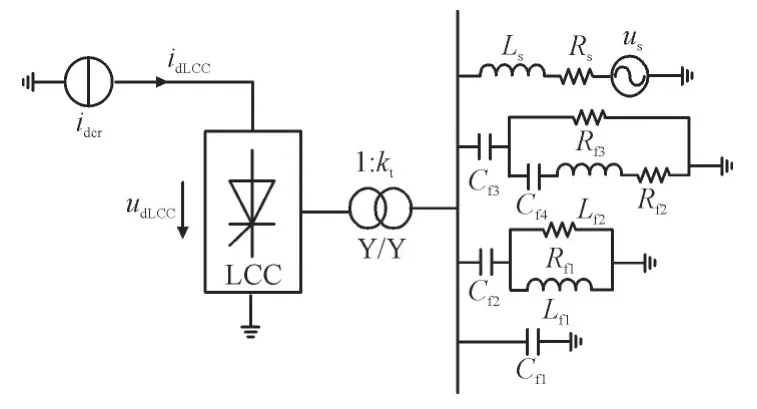
图7 LCC逆变站模型示意图Fig.7 Schematic of inverter station model of LCC

2）系统B：LCC 运行在整流状态，定直流电流控制，直流输电线路采用T 型等效，系统电路如图8所示，具体参数如表2 所示。图8 和表2 中udci为逆变侧等效电压源，kpr，kir分别为定直流电流控制的PI比例和积分参数，Gr，Tr分别为定直流电流控制的一阶滤波参数，Line，Cline，Rline为T 型等效直流线路的电感、电容和电阻参数。

表2 整流站LCC直流输电仿真系统参数Table 2 Parameters of rectifier station LCC DC transmission simulation system

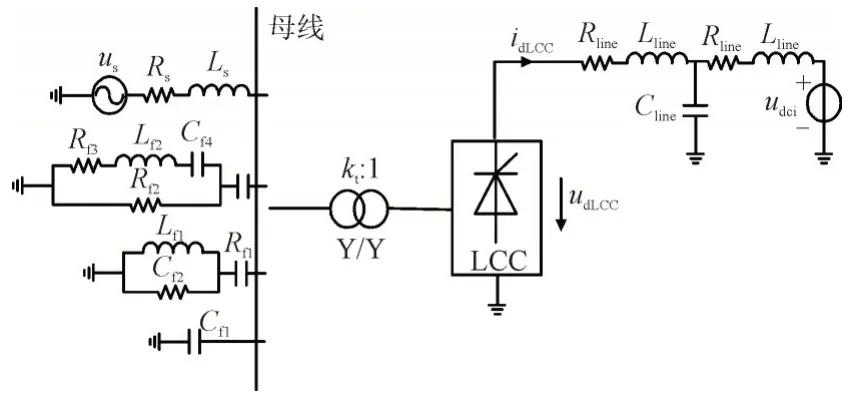
图8 LCC整流站模型示意图Fig.8 Schematic of rectifier station model of LCC

3）系统C：由系统A 和B 构成的双端系统。

分别仿真运行系统A，B，C，并进行直流侧阻抗扫描，再将扫描结果与本文提出的简化阻抗模型以及基于未统一的电压电流开关函数得到的阻抗模型进行对比，系统A，B，C 的对比结果分别如图9、图10、图11 所示，其中图11 为逆变侧看向整流侧的直流阻抗，即整流侧LCC 直流阻抗和直流线路阻抗之和。

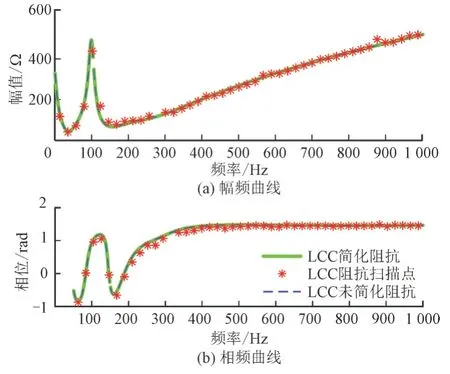
图9 系统A直流侧阻抗对比图Fig.9 DC impedance comparison of system A

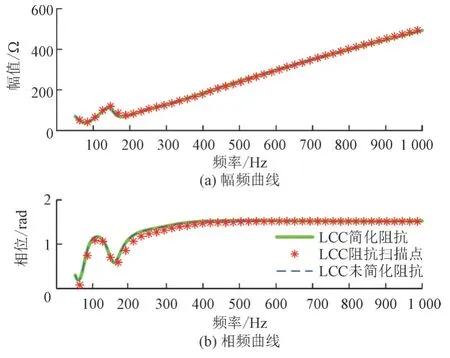
图10 系统B直流侧阻抗对比图Fig.10 DC impedance comparison of system B

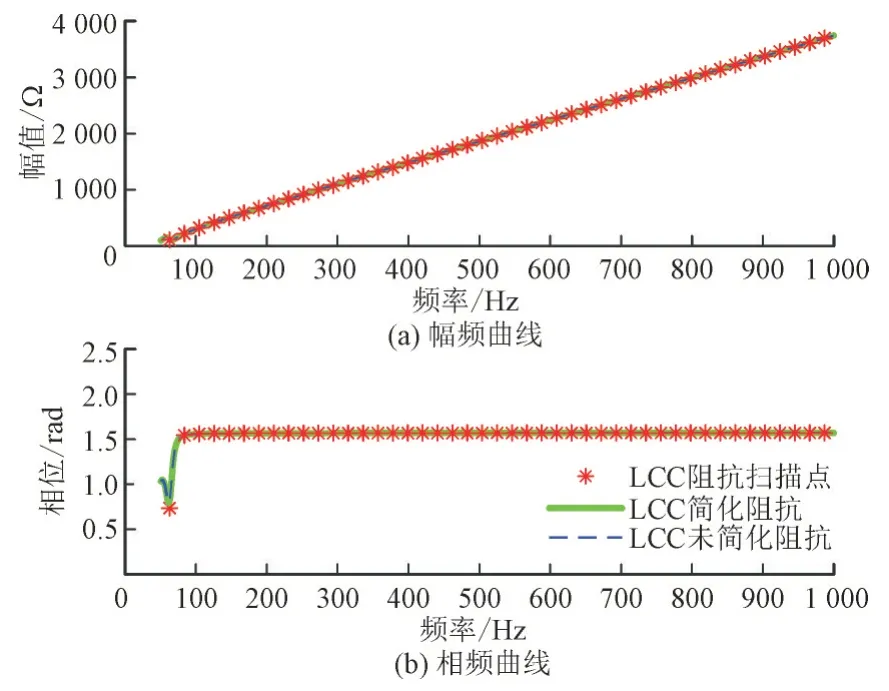
图11 系统C直流侧阻抗对比图Fig.11 DC impedance comparison of system C

图9、图10 和图11 中绿色实线为本文提出的基于简化开关函数模型得到的LCC 阻抗，蓝色虚线为基于未简化的开关函数模型得到的LCC 阻抗，红色星号线为LCC 阻抗扫描值。从图9、图10 和图11 可以看出：

1）本文提出的简化阻抗模型与未简化的阻抗模型法相吻合，二者曲线几乎相重合。

2）计算结果与仿真扫频结果基本相吻合，除了靠近200 Hz 附近的相位误差稍大之外，其余相位误差与幅值误差比较小。

3）无论是整流站LCC、逆变站LCC 还是双端LCC，本文方法均能得到较为准确的阻抗计算结果。

4）以上说明本文简化方法有效。

4 结论

针对实际工程中快速建立LCC-HVDC 系统小信号模型以及时分析系统稳定性的需求，结合LCC换相过程进行数学推导，提出了一种LCC 简化开关函数模型，统一了电压和电流开关函数，为LCC 考虑换相过程的建模提供了一种新的思路。基于提出的简化开关函数模型，通过动态相量法和交直流侧的谐波传递分析，建立了LCC 的直流阻抗模型和未简化的直流侧阻抗模型相比，本文提出的模型在拥有同样精度的条件下占用内存更小、计算速度更快、计算效率更高，可用于LCC-HVDC 工程的阻抗快速计算和稳定性分析。

本文提出的基于简化开关函数的阻抗建模方法适用于复杂的直流输电场合，未来将在本文的基础上将该方法应用到结构更加复杂的混合多端直流输电系统中，对混合多端直流输电系统的简化阻抗建模方法和稳定性分析展开深入研究。