基于双层优化的电-热综合能源系统调峰运行方法

柳松林，成贵学，赵晋斌，蒋明喆，李健明

（1.上海电力大学，上海 201306；2.国网蚌埠供电公司，安徽蚌埠 233000）

0 引言

随着我国能源结构的调整[1-2]，综合能源系统（Integrated Energy System，IES）的提出加快了多类型能源网络在发电、变电、输电、配电、用电等各个环节的耦合互联[3-5]。随着新能源装机总容量的不断增长，高比例的新能源在并网后会增大电网负荷的峰谷波动，降低系统的峰谷调节能力[6]。不同类型能源网络间的强耦合性也会增大电网负荷的峰谷波动。因此，利用IES 理论与技术寻找有效的优化调度方法，对改善系统的峰谷波动和运行经济性具有重要的意义[7-9]。

为解决高比例新能源并网引起的调峰能力不足问题，有关学者提出了一系列调峰方法，包括多源协调的储能模型[10-11]、基于IES 的优化控制[12-13]等。文献[14]从最优弃能率角度出发，提出一种分层优化模型用于提升电网的峰谷调节能力。但其仅从源侧对电网的调节能力进行分析，忽略了荷侧负荷具备可调度的可能性。因此，探讨基于荷侧灵活性资源的调峰策略，可以进一步提升电网的峰谷调节能力和运行经济性。

荷侧资源具有灵活性和经济性的优化调度潜力，尤其在改善电网峰谷波动方面具有显著的作用。文献[15]通过建立需求响应（Demand Response，DR）模型，引导荷侧资源参与电网功率调节。文献[16]针对高比例风电并网带来的调峰压力，建立计及需求响应的风电优化调度模型，验证了荷侧资源在缓解电网调峰方面的有效性。文献[17]从荷侧多类型能源耦合的角度，提出了一种用于削峰填谷控制的IES 模型，进一步提升了电网调峰能力。

国内外研究人员从多时间尺度[18-20]角度提出了源荷侧协同优化的调度模型。文献[21]建立了计及DR 的源荷侧协同调峰优化模型，可以有效调节负荷峰谷。但是传统的源荷侧协同优化的调度模型往往依赖于IES 数据的精准预测，在面临不确定性场景时存在偏差。文献[22-23]引入强化学习（Reinforcement Learning，RL）算法对IES 进行动态优化。文献[24]提出了基于深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG）强化学习算法的优化调度模型，进一步提高了复杂场景下IES 的优化效果。

因此，本文提出一种基于IES 源荷侧协同的调峰运行方法和双层优化调度模型。首先，分析了不同比例的风光并网功率对电负荷峰谷的影响，并建立综合需求响应（Integrated Demand Response，IDR）的调峰模型。其次，考虑IES 的峰谷调节能力和运行经济性，构建了一种双层优化调度的电-热IES 模型，其上层模型采用传统的优化方法平滑电网负荷曲线，下层模型采用DDPG 算法优化IES 的运行经济性。最后，以某高校实际微能源系统作为算例，验证了本文所提运行方法和模型的有效性。

1 IES源荷侧协同调峰分析

1.1 风光并网功率对电网负荷的影响

近年来，我国以风电、光电为代表的新能源迅速发展。基于电力系统中供需平衡的原理，电网负荷曲线受到新能源并网功率的影响，在全额并网消纳后会增大电网负荷的峰谷差。此外，风电和光电输出功率受自然因素影响，其功率变化具有一定的规律性。典型日新能源及电负荷预测曲线如图1所示。

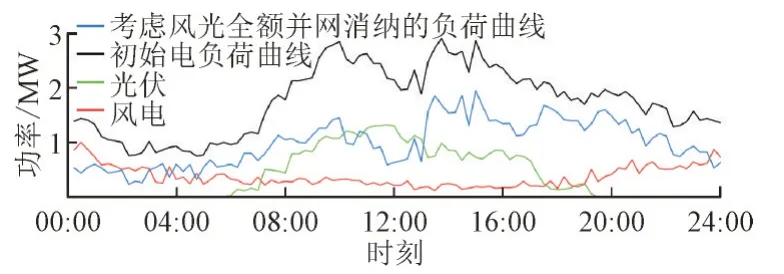
图1 典型日新能源及电负荷预测曲线Fig.1 Forecasting curve of renewable energy and electric load on typical day

由图1 可知，风电与电负荷功率变化趋势相反，即00:00—07:00 和18:00—24:00 时段电负荷水平较低时风电功率较高，07:00—18:00 时段电负荷水平较高时风电的功率较低，反调峰特性明显。而光电与风电变化趋势完全相反。这类负荷特性由新能源发电的固有特点决定，在我国的新能源开发中比较典型。

因此，新能源并网给电网运行带来困难，尤其在大量新能源并网时更加明显。为此需要对系统进行合理地优化，以发挥新能源的优势，提高系统的可靠性和经济性。

1.2 IDR模型

本文考虑负荷具备横向DR 和纵向DR 的能力，根据负荷的特性，数学建模为：

式中：PL(t)，P0,L(t)，ΔPL(t)分别为t时段IDR 后的负荷功率、IDR 前的负荷功率与IDR 负荷的改变量；分别为t时段IDR 后的负荷转移改变量与IDR 后的负荷替代改变量；αmax为系统允许的最大负荷变化率。

1）转移负荷。转移负荷指在调度周期（1d）内进行用能时段转移的负荷。数学建模为：

2）替代负荷。替代负荷指同一时段选择不同的能源类型满足负荷侧等质的用能需求的负荷。数学建模为：

2 IES源荷侧双层优化调度模型

本文基于IES 建立源荷侧协同的双层优化调度模型，如图2 所示。其中，其上层模型为调节电网负荷的峰谷波动，下层模型为IES 的优化调度。

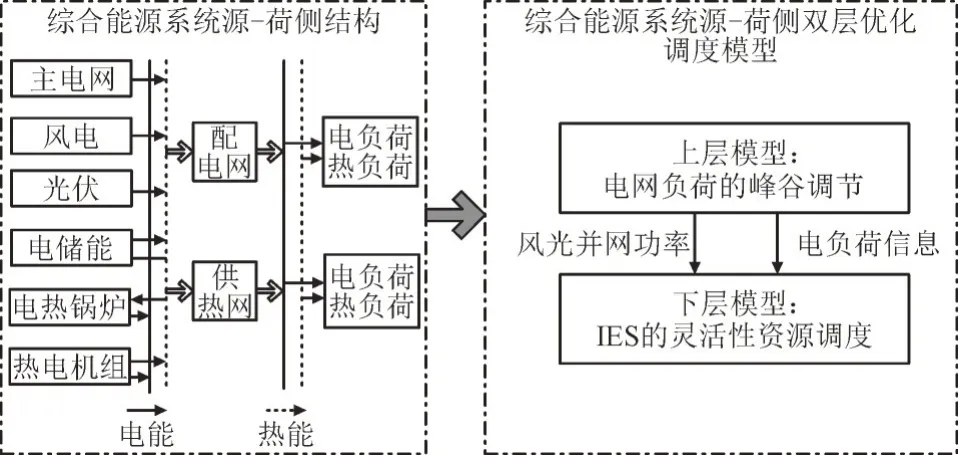
图2 IES结构与源荷侧双层优化调度模型框架图Fig.2 IES structure and source load side bi-level optimization dispatch model

2.1 上层模型

2.1.1 目标函数

为抑制电网负荷波动，上层模型采用最小二乘法建立目标函数，数学建模为：

式中：F1为负荷侧电网的负荷方差；Pg(t)，Pg,avg分别为t时段电网负荷与调度周期T内电网的平均负荷；Ppv(t)，Pwt(t)分别为t时段光电与风电的最优并网功率；P0,pv(t)，P0,wt(t)分别为t时段光电和风电的预测出力；μpv(t)，μwt(t)分别为t时段光电与风电的最优并网系数。

2.1.2 运行约束

1）并网约束为：

2）弃能约束为：

式中：βwt,max，βpv,max分别为最大允许的弃风系数和弃光系数。

2.2 下层模型

2.2.1 目标函数

下层模型以IES 在调度周期T内的总运行成本最小为目标函数。数学建模为：

1）从主电网购电的成本C1为：

式中：Pnet(t)为t时段IES 向主电网购电的功率；εe(t)为t时段的购电电价。

2）热电机组（Combined Heat and Power，CHP）的运行成本C2为：

式中：Pchp(t)，Hchp(t)分别为t时段CHP 发出的电功率与热功率；achp，bchp，cchp分别为CHP 的运行成本系数；cv1，cv2分别为CHP 的最小进汽工况斜率和最大进汽工况斜率。

3）电储能设备（Battery，BA）的折旧成本C3为：

式中：Pba(t)为t时段BA 设备充电/放电的功率，若Pba(t)>0，表示t时段BA 设备处于放电状态，若Pba(t)<0，表示t时段BA 设备处于充电状态，若Pba(t)=0，表示t时段BA 设备处于静置状态；ρba为BA 设备的折旧系数。

4）CO2排放惩罚成本C4为：

2.2.2 运行约束

1）电/热功率平衡约束为：

式中：Pchp,g(t)，Peb(t) 为t时段CHP 与电热锅炉（Electric Boiler，EB）的并网功率；Hchp(t)，Heb(t)为t时段CHP 和EB 输出的热功率；HL(t)为t时段的热负荷需求。

2）与主电网联络线约束为：

式中：Pnet,min，Pnet,max分别为主电网联络线向IES 注入电功率的下限和上限。

3）设备运行约束。

（1）CHP 设备约束为：

式中：b为CHP 的热电比；Hchp,min，Hchp,max分别为CHP 输出热功率的下限与上限；Pchp,ccs(t)为t时段CHP 的碳捕集系统（Carbon Capture System，CCS）捕捉CO2消耗的电功率；为t时段CCS 捕捉的CO2量；ϕ为捕捉单位的CO2量所需电功率；，分别为CHP 的CO2排放系数。。

（2）EB 设备约束为：

式中：ηeb为EB 设备的制热效率；Heb,min，Heb,max分别为EB 输出热功率的下限和上限。

（3）BA 设备约束为：

式中：Soc(t)为t时段BA 的荷电状态；Soc,min，Soc,max为BA 的下限与上限；Pba,max，Pba,min分别为BA 设备充/放电功率的上限与下限；Qba为BA 设备的容量；ηba为BA 设备的充/放电系数，其数学建模为：

式中：ηch，ηdis分别为电储能设备的充电系数和放电系数。

3 双层模型求解方法

本文所提源荷侧协同的双层优化调度模型采用双阶段求解方法，如图3 所示。其中，St，St+1分别为t，t+1 时段RL 智能体的状态值；Rt，Rt+1分别为t，t+1时段RL 智能体获得奖励值。

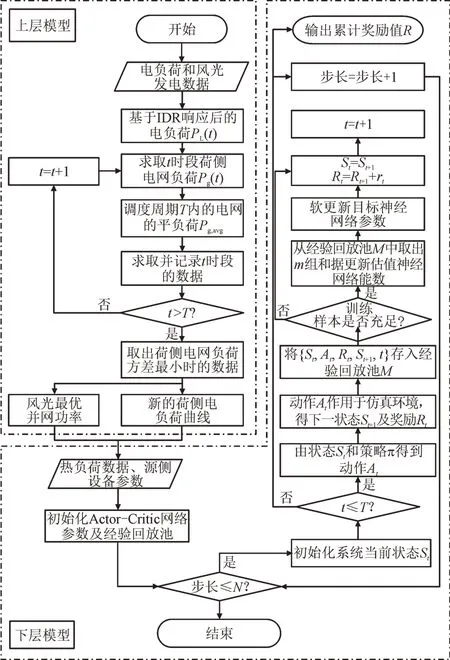
图3 IES源荷侧双层优化调度模型求解流程Fig.3 Solving process of IES source-load side bi-level optimal dispatch model

本文所提模型求解方法中，上层模型使用商业求解器Groubi 优化各时段的风光并网功率和电网负荷功率，并将求解结果传递到下层模型。

下层模型基于Actor-Critic 框架的DDPG 强化学习算法，求解得到最优的IES 调度方案。RL 智能体通过不断与IES 环境交互试错，通过评估动作-值函数Qπ(S,A)，寻找最优的策略π，以获得最大化累计奖励R，即：

式中：S为IES 环境的状态空间；a为RL 智能体动作；A为RL 智能体的动作空间；Eπ(∙)为策略π的期望；φ为折扣因子，φ∈[0,1]。

RL 智能体在t时段观测到环境状态St后，基于策略π生成的动作At作用于环境，得到当前t时段的奖励Rt，RL 智能体进入到下一个环境状态St+1。将这一过程得到的经验(St,At,Rt,St+1)存储在经验回放池M中，用于RL 智能体训练时更新估值神经网络参数。RL 智能体在训练学习过程中，以IES 总运行成本最小为目标函数训练DDPG 算法的神经网络，训练结束后即可用于IES 的优化调度。对IES 的状态空间、动作空间和奖励函数进行设计。

1）状态空间。IES 的状态空间St为5 维状态，数学建模为：

2）动作空间。IES 的动作空间At为2 维动作，数学建模为：

3）奖励函数。IES 的奖励函数Rt(St,At)为RL智能体在t时刻获得的最大化奖励，数学建模为：

4 算例验证

4.1 算例配置

本文以华东地区某高校的实际微能源系统为研究对象，系统的风电、光电和电/热负荷数据采集于2020 年6 月22 日—2020 年6 月30 日，如图4 所示。

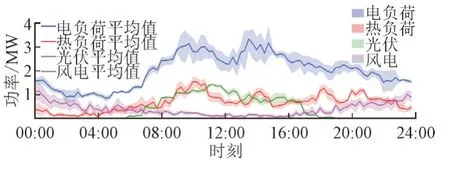
图4 微能源系统的历史数据Fig.4 Historical data of micro-energy systems

本文设置DDPG 算法的估值神经网络和目标神经网络的隐含层均为2 层，大小分别为256 和128，激活函数为tanh 函数，其他参数请参考文献[18-19]。IES 的调度周期为24 h，间隔时段为15 min，并使用6 月22 日—6 月29 日的数据进行训练，使用6 月30 日的数据进行测试。本文采用分时电价，如表1所示。其中，峰时段为07:00—15:00，平时段15:00—23:00，谷时段为00:00—07:00，23:00—24:00。

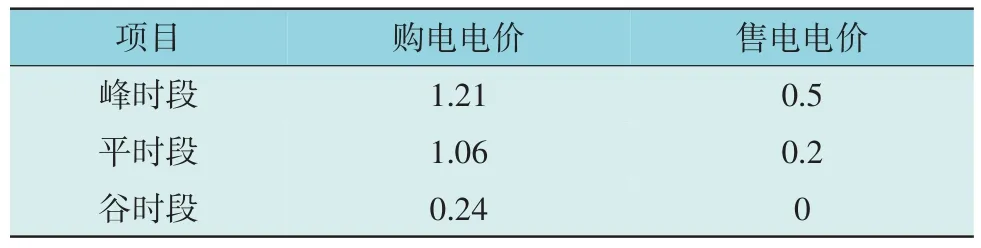
表1 电价划分Table 1 Electricity price division [元·(kWh)-1]

4.2 优化调度结果

4.2.1 上层模型调度结果

图5 为各时段最优的风光并网功率。在整个调度周期内，光电的并网率大于风电的并网率，光电和风电并网率分别为94.86%和57.47%。在峰时段和平时段，风电和光电的发电功率大部分被并网消纳，这是由于在峰时段和平时段的新能源发电功率和负荷需求量较高所致。而在谷时段，风电的并网功率处在较低的水平，甚至在02:00—06:00 时段风电并网率最小为0，这是由于在谷时段电网负荷的需求量较低，尽管风电功率在整个调度周期内处于较高水平，但由于电网负荷的限制，风电功率并未充分利用。因此，上层模型可以在保证风光并网消纳率最大的前提下，实现对电网负荷的调峰运行。

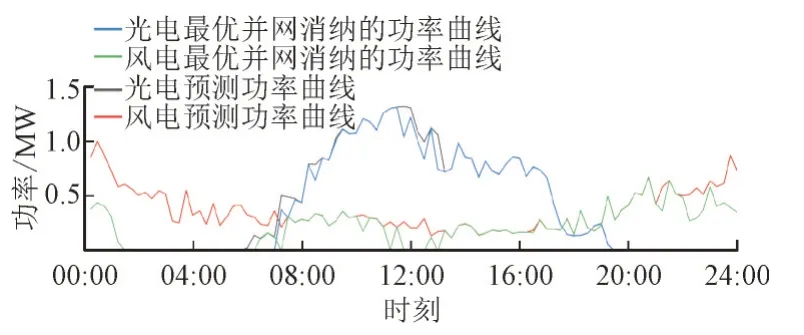
图5 各时段最优的风光并网功率Fig.5 Optimal WPV grid-connected power at each time

图6 为电负荷的IDR 调度结果。根据电负荷需求的特点，13:00—21:00 时段通过减少电负荷曲线的“峰值”，即利用转移负荷将该时段的部分用电需求转移至谷时段。00：00—07:00 和22:00—24:00时段通过增加电负荷曲线的“谷值”，即峰时段或平时段的部分用电需求通过转移负荷的方式至该时段。此外，负荷侧优化更倾向于将峰时段或平时段的部分用电需求用其他类型能源替代。

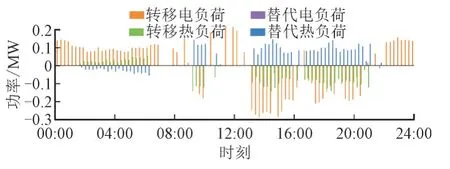
图6 电负荷的IDR调度结果Fig.6 IDR dispatching result of electrical load

通过源荷侧协同调峰运行方法可以抑制电网负荷的波动，实现电网负荷曲线的“削峰填谷”。电负荷曲线和考虑风光并网后的电网负荷曲线在经过上层模型平滑优化后，如图7 所示，不仅降低了电网负荷的峰谷差还提升了电网的调峰能力。由图7 可知，初始电负荷功率曲线的峰谷差为2.16 MW。当风电和光电的出力功率被全额并网消纳后，此时电网的负荷变化率较大，电网负荷曲线的峰谷差为1.81 MW。通过本文所提的调峰运行方法优化后，电网负荷曲线的最大峰谷差仅为0.7 MW。因此，经过本文所提的上层模型优化后，不仅可以抑制电网负荷曲线的波动，还保证了较高的风光消纳率。

4.2.2 下层模型调度结果

图8 和图9 分别为IES 的电功率调度结果和热功率调度结果。由图8—图9 可知，IES 购电量与电价成反比，即在电价较高时购电量较少，在电价较低时购电量较多。在峰时段和平时段，除风光并网功率外，由于CHP 的“以热定电”约束，使CHP 的发电功率也处于较高水平，电储能设备则适时对外放电；在谷时段，CHP 的电出力基本用于CCS，如图10 所示，除风电并网功率外，IES 主要提高购电量以满足负荷侧的用电需求，并将多余的电能储存在BA 中，以用于后续时段调度的使用。IES 的热负荷主要由CHP供应，当热负荷高于1.2MW 时，仅靠CHP 的热出力供热无法满足时，电热锅炉启动承担热负荷的调峰。

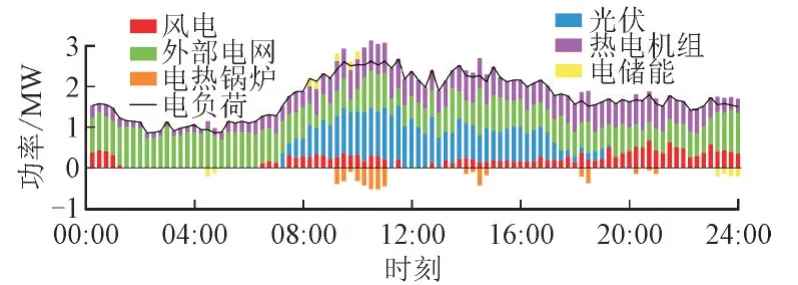
图8 电功率调度结果Fig.8 Dispatching result of electric power

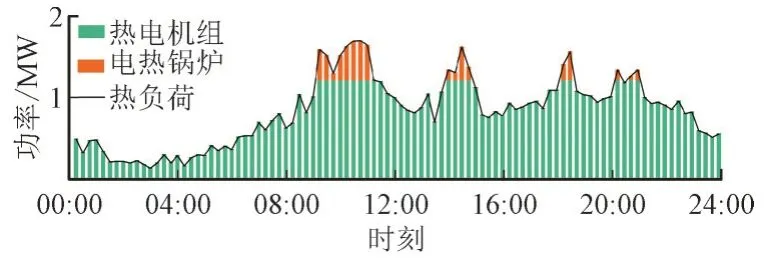
图9 热功率调度结果Fig.9 Dispatching result of heat power

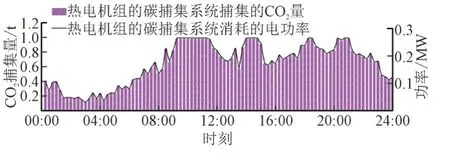
图10 CHP的CCS捕集的CO2量与所消耗的电功率关系Fig.10 Relationship between CO2 capture amount and electrical power consumed by CCS of CHP

由图10 可知，在调度周期T内，CCS 消耗的电功率与CCS 捕集的CO2量成正比。通过捕集CHP运行程中产生的CO2并将其封存在地下或其他储存设施中，以减少CO2气体排放。因此，含CCS 的CHP 在IES 中运行时，在减少IES 的运行成本和实现IES 的低碳运行方面具有较好的效果。

综上所述，下层模型能够动态的优化IES 中各设备的运行状态，在提高IES 的经济性和实现IES的低碳运行方面具有有效性。

4.3 对比分析

为验证本文所提出的IES 源荷侧协同运行方法的经济性和其在不同负荷特性上的普适性，设立工作日和周末2 个不同时段的4 个场景进行对比分析。场景1：不考虑调峰运行，利用Gurobi 求解；场景2：考虑荷侧IDR 调峰运行，利用Gurobi 求解；场景3：考虑源荷侧协同的调峰运行，利用Gurobi 求解；场景4：考虑源荷侧协同的调峰运行，利用Gurobi+DDPG 算法求解。工作日和周末各场景下的IES 运行成本如表2 所示。

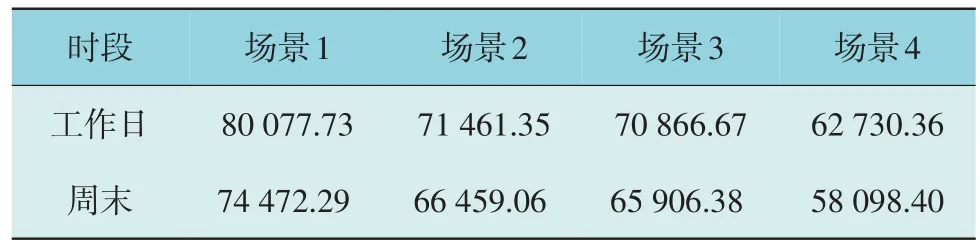
表2 各场景下的IES运行成本Table 2 Operating cost of IES under each scenario 元

由表2 可知，场景1 中的IES 运行成本在工作日和周末均最高。场景2 相较于场景1，由于考虑荷侧IDR 调峰运行，IES 能够根据负荷特性和能源价格进行优化，使IES 运行成本有所降低。场景3相对与场景2，考虑了源荷侧协同的调峰运行，实现经济高效地IES 运行。场景4 相较于场景3，由于引入了DDPG 算法，能够更加准确地预测负荷特性和价格信号，源荷侧协同调峰得到进一步优化，使IES 运行更加经济。综上所述，本文所提出的IES源荷侧协同运行方法，能够显著降低IES 的运行成本，具有一定的普适性。

5 结语

为解决高比例风光并网引起的电网峰谷波动，本文提出了一种源荷侧协同调峰的运行方法和双层优化调度模型，并通过算例验证了本文所提方法在平抑电网负荷波动、提高IES 的峰谷调节能力和提高IES 的经济性具有显著的效果。