基于SC的光伏发电并网系统次同步振荡抑制方法

祁晓笑，程 静，王维庆，于永军，王小云

（1.新疆电力系统全过程仿真重点实验室，新疆乌鲁木齐 830011；2.新疆大学电气工程学院，新疆乌鲁木齐 830017；3.国网新疆电力有限公司电力科学研究院，新疆乌鲁木齐 830011）

0 引言

在“双碳”目标和以新能源为主体的新型电力系统转型推动下，新能源发电量占比显著提升，由于其发电的不确定性和间歇性及新型电力系统的高电力电子化特征带来的非线性、多尺度、强耦合特性，对电力系统的安全稳定运行产生影响[1-3]。近年来，因次同步振荡（Sub-Synchronous Oscillation，SSO）引发的电力系统故障事件在国内外频繁发生，亟需找到有效的振荡抑制方法[4-6]。

针对新能源并网电力系统的SSO 问题，国内外学者开展了探索与研究。文献[7]分析了永磁风机经柔直系统接入电网的振荡问题。文献[8]揭示了风电场与串补线路交互作用的SSO 风险。文献[9]和文献[10-11]分别针对双馈风电场和直驱风电场引发的SSO 问题提出抑制方法。文献[12]提出了一种改进的复转矩系数法，分析了多风电场与多机系统交互的轴系SSO 引发原因。文献[13]采用附加频变增益控制策略抑制风力发电与输电系统间交互作用引发的SSO。文献[14]以最优控制理论对双馈风电场设计了反馈控制器抑制SSO。文献[15]针对多机系统采用STATCOM 方法实现 SSO 抑制。近年来，随着直流高压/特高压及新能源技术的发展，电力系统电力电子化程度不断提高，引起惯量和阻尼大幅下降，对系统稳定性带来严重影响。因同步调相机（Synchronous Condenser，SC）优越的无功补偿性能、次暂态特性，同时可促进提升系统的惯量和阻尼，被重新受到关注[16-18]，国网公司拟投装大批300Mvar 同步调相机以提升电网支撑强度。文献[19]将新一代大容量调相机应用于特高压直流输电系统，以降低新能源脱网和换相失败风险。文献[20]提出了调相机无功补偿优化方案，解决高比例新能源送出的暂态过电压问题。文献[21]针对高比例新能源接入的西北电网送端电压支撑能力减弱问题，研究了调相机优化配置方法。目前，调相机主要被应用于变电站，为高压直流换流过程提供电压支撑，对其在SSO 抑制方面的应用近期才被引起关注。文献[22]提出了一种抑制新能源发电引起SSO 的方法，应用于新能源基地和高压直流换流，取得初步成效。文献[23]以阻抗法分析了SC 抑制SSO 的机理及可行性。对进一步改善调相机抑制SSO 效果方面有待深入研究更有效的方法。

因此，本文对基于新一代调相机的光伏发电并网系统次同步振荡抑制方法进行研究，对新一代调相机的功能拓展开发利用，实现光伏发电并网系统次同步振荡的有效抑制。

1 光伏发电并网系统综合模型

光伏发电并网系统结构示意图如图1 所示，由光伏阵列及最大功率跟踪（Maximum Power Point Tracking，MPPT）控制、DC-DC 变换器、逆变器及其控制系统、脉宽调制（Pulse Width Modulation，PWM）、LCL 滤波器、锁相环（Phase-Locked Loop，PLL）和SC等组成。

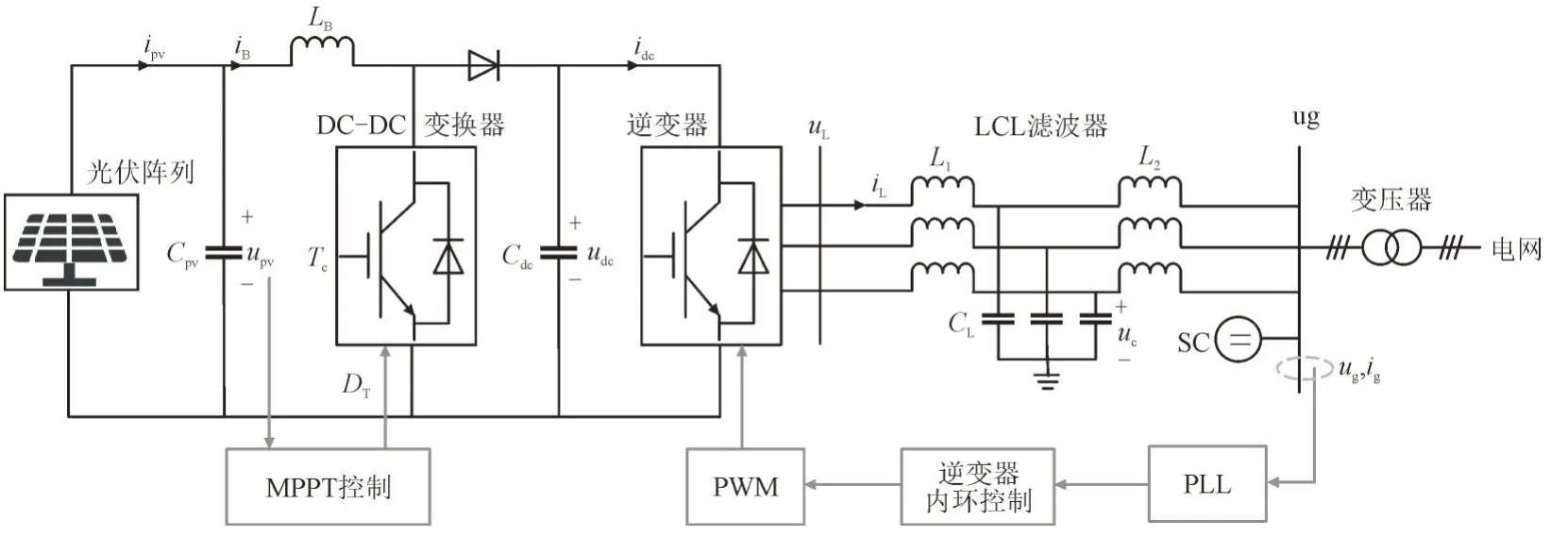
图1 光伏发电并网系统结构示意图Fig.1 Structure diagram of photovoltaic power generation grid-connected system

图1 中，ipv和upv为光伏阵列的输出电流和电压；Cpv为光伏阵列的滤波电容；iB为流过滤波电感LB的电流；Tc和DT分别为DC-DC 变换器的触发脉冲和脉冲的占空比；udc为变换器输出侧直流电容Cdc的端电压；idc为逆变器输入电流；uL为逆变器输出电压；CL，L1和L2分别为LCL 滤波器的滤波电容、左桥臂电感和右桥臂电感；iL为滤波电感L1中的电流；uc为CL的端电压；ug和ig分别为LCL 滤波器输出电压和输出电流。

1.1 光伏电池及MPPT控制建模

由光伏电池的短路电流isc、开路电压uoc、最大电流im及最大电压um4 个电气参数描述其伏安特性，如式（1）所示：

式中：C1和C2为引入的中间变量。

比较光伏阵列输出端口电压upv与最优电压Upv，以其电压差值调节DC-DC 变换器的触发脉冲Tc的占空比DT，实现实时光辐照度和温度下的电池最大功率输出。MPPT 控制结构框图如图2 所示。

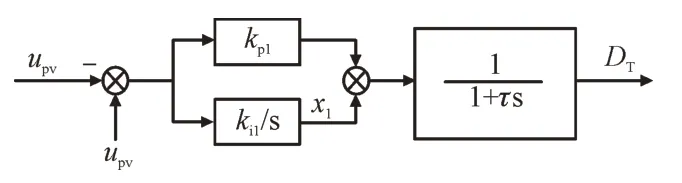
图2 MPPT控制结构框图Fig.2 MPPT control structure block diagram

MPPT 控制方程如式（2）所示：

式中：kp1和ki1分别为比例和积分控制系数；x1为引入的中间变量；τ为时间常数；s 为拉普拉斯变换的复平面微分算子。

1.2 DC-DC变换器模型

DC-DC 变换器的电压和电流关系表述为[24]：

忽略逆变器开关损耗，光伏阵列输出功率等效于直流电容与逆变器功率总和。有：

式中：uLd，uLq和iLd，iLq分别为逆变器输出电压uL和电流iL的d，q轴分量。

1.3 逆变器及其控制系统建模

逆变器是将直流电变换为与电网等幅、同频正弦交流电的重要环节，其控制框图如图3 所示。

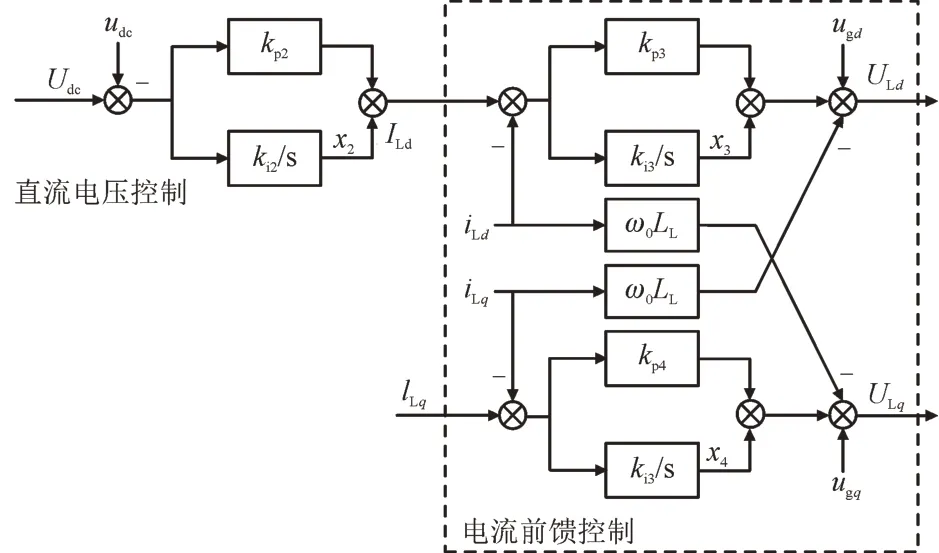
图3 逆变器控制结构框图Fig.3 Inverter control structure block diagram

图3 中，Udc为直流电容Cdc的端电压参考值；kp2和ki2为逆变器直流电压控制外环的比例和积分系数；kp3，kp4和ki3，ki4分别为d，q轴电流内环的比例和积分系数；ugd，ugq为LCL 滤波器输出电压的d，q轴分量；ULd，ULq为逆变器输出控制电压的d，q轴分量；ILd，ILq为内环控制的参考电流d，q轴分量；ω0为电网电压角频率基准值；LL为LCL滤波器电路等效电感；x2～x4为引入的中间状态变量。

逆变器及其控制系统的数学模型表示为：

式中：ugd，ugq和igd，igq分别为LCL 滤波器输出电压ug和输出电流ig的d，q轴分量。

1.4 锁相环数学模型

锁相环实时跟踪光伏发电系统输出端口的电压相位，保证并网电压与电网电压同相同频，其控制框图如图4 所示。

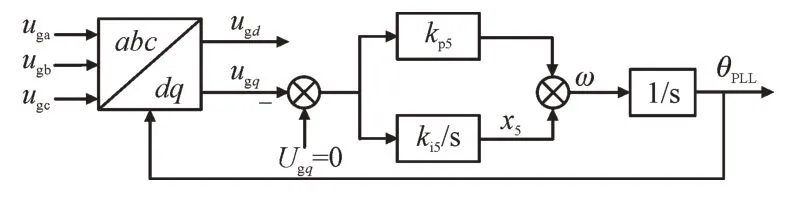
图4 PLL控制框图Fig.4 PLL control block diagram

图4 中，uga，ugb，ugc和ugq分别为逆变和滤波后的三相电压及其q轴参考电压；kp5，ki5为锁相环比例和积分系数；ω为电网电压角频率；θPLL为锁相环输出的电压相位。

引入中间变量x5，得其状态方程：

式中：Δx为变量x5的线性微分量。

1.5 滤波器数学模型

将LCL 滤波器的左右桥臂电感进行归算，得到图1 中简化的滤波器等效电路模型，如图5 所示。

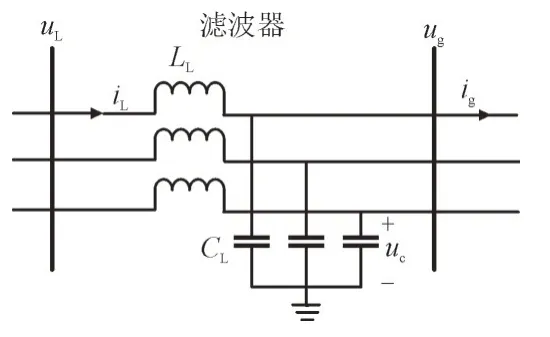
图5 滤波器简化模型Fig.5 Simplified model of filter

滤波器电路的状态方程为：

1.6 同步调相机数学模型

同步调相机是一个具有多变量、非线性、强耦合结构的设备，用以提供快速动态无功补偿。在dq旋转坐标系中，建立同步调相机数学模型，如式（8）所示：

式中：δ为调相机功角；ωSC和ωSC0为调相机转子角速度及其基准值；Pe为电磁功率；D和TJ分别为阻尼系数和惯量系数；T′d0为d轴暂态开路时间常数；Xd，X′d和Xq，X′q分别为d，q轴的同步电抗和暂态电抗；uSCd，uSCq和iSCd，iSCq分别为调相机的d，q轴电压和电流；Efq为q轴励磁电压；E′q为q轴暂态电动势；Rs为定子绕组电阻。

调相机输出的有功PSC和无功QSC分别为：

式中：m为发电机相数；Eq为q轴电动势；U为调相机端电压。

1.7 光伏发电并网系统精细化整体模型

光伏发电系统注入电网的有功Pg和无功Qg为：

式中：ugd，ugq和igd，igq分别为电网电压和电流的d，q轴分量。

联立式（1）—式（10）并线性化，得到光伏发电并网系统精细化整体状态空间模型，简化表述为：

式中：x为系统的状态变量矩阵，x=[upv,iB,udc,DT,x1,x2,x3,x4,x5,θPLL,iLd,iLq,ucd,ucq,igd,igq,iSCd,iSCq]T；y为输出变量矩阵，y=[Pg,Qg,PSC,QSC]T；u为输入变量矩阵，u=[ugd,ugq]T。

1.4 AchE 抑制剂处理细胞 用二甲基亚砜（dimethyl sulfoxide，DMSO）溶解 2 种 AchE 抑制剂 Done 和 Ito，制备浓度分别为 10 mmol/L 和 50 mmol/L 的储存液。首先检测 AchE 抑制剂 Ito 和Done 的细胞毒性。将 Huh7 细胞接种到 96 孔板中，当细胞融合度达到 70% 时将抑制剂分别稀释成 60、125、250、500 μmol/L 4 个浓度梯度处理细胞，60 h 后用 CCK-8 检测细胞增殖水平。

将式（11）在平衡点x0处泰勒展开，略去高阶无穷小量，进一步整理可得：

2 SC抑制次同步振荡的原理

新能源并网电力系统中宽频振荡多由线路中的短路扰动故障引发，且各频段振荡均与无功补偿电路高度相关，同步调相机的快速无功补偿特性能够促进系统受扰后快速恢复稳定[18]。SC 抑制次同步振荡的方法流程如图6 所示。

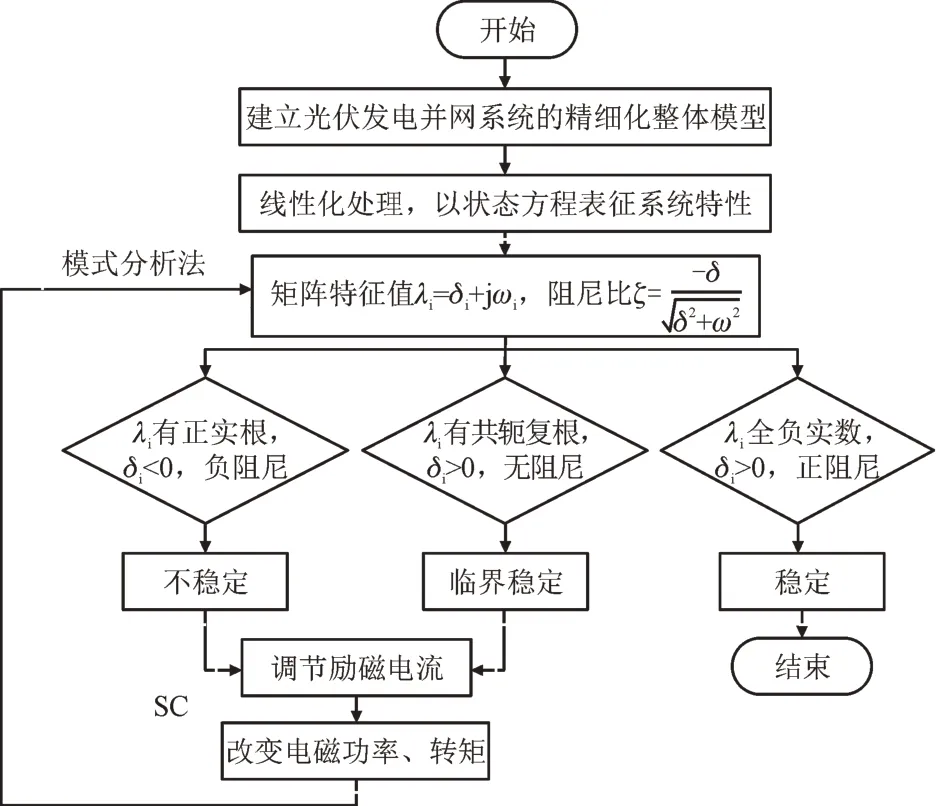
图6 SC抑制次同步振荡方法流程Fig.6 Process of SSO with SC suppression

建立精细化表征光伏发电并网系统特性的线性化整体模型，求解状态方程雅可比矩阵A的n个特征值λi=δi+jωi（i=1，2，…，n；δi和ωi为每组特征值的实部和虚部）和阻尼比ζi=；依据Lyapunov 第一稳定判据，以模式分析法分析判断系统动态响应特性。对于不稳定或临界稳定系统，通过调节调相机励磁电流改变其电磁功率和转矩，从而改变系统特征值分布情况，消除引起次同步振荡的不稳定因素，抑制振荡发生。

2.1 模式分析法判断系统稳定性

非线性系统的小干扰稳定性由雅可比矩阵A的特征值λi决定，动态响应的振荡模态衰减速度与阻尼比相关。具体情况有以下3 种：（1）λi存在正实数时，即对应的特征根位于S 右半平面，δi<0，系统呈负阻尼，其动态响应过程呈发散模态，系统不稳定；（2）存在λi=±jωi这样的共轭复根时，即对应的特征根位于虚轴上，δi=0，系统无阻尼，其动态响应过程为等幅振荡模态，系统临界稳定；（3）当δi>0 时，系统呈正阻尼，其动态响应过程呈收敛模态，稳定。综上可知，当δi=0 时，系统发生振荡。

2.2 SC抑制次同步振荡原理

当系统受到小干扰或短路故障等扰动时，调相机将产生电磁转矩ΔTSC，它与发电机转速偏差ΔωSC而产生电磁转矩ΔTe，二者关系如图7 所示。

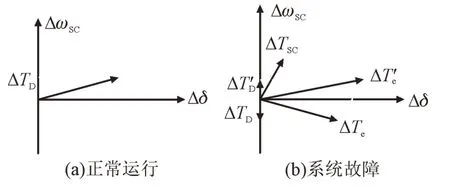
图7 SC抑制次同步振荡向量图Fig.7 Vector graph of SSO with SC suppression

当系统正常运行时，发电机电磁转矩ΔTe位于第一象限，其纵分量电气阻尼转矩ΔTD为正。当发生振荡时，随功率角Δδ的变化，发电机电磁转矩ΔTe位于第三或四象限，其纵分量电气阻尼转矩ΔTD为负，系统处于不稳定状态。加入同步调相机后，为系统提供第一象限的电磁转矩ΔTSC，与ΔTe合成ΔT′e，可使ΔTD由负变为正ΔT′D，保障系统稳定，抑制次同步振荡。

3 仿真分析与验证

3.1 抑制IEEE次同步振荡第一标准型系统的SSO

在Matlab/simulink 软件平台搭建IEEE 次同步振荡第一标准型系统模型。对比加入调相机前后系统并网参量的变化，验证同步调相机对次同步振荡的抑制效果，如图8 所示。

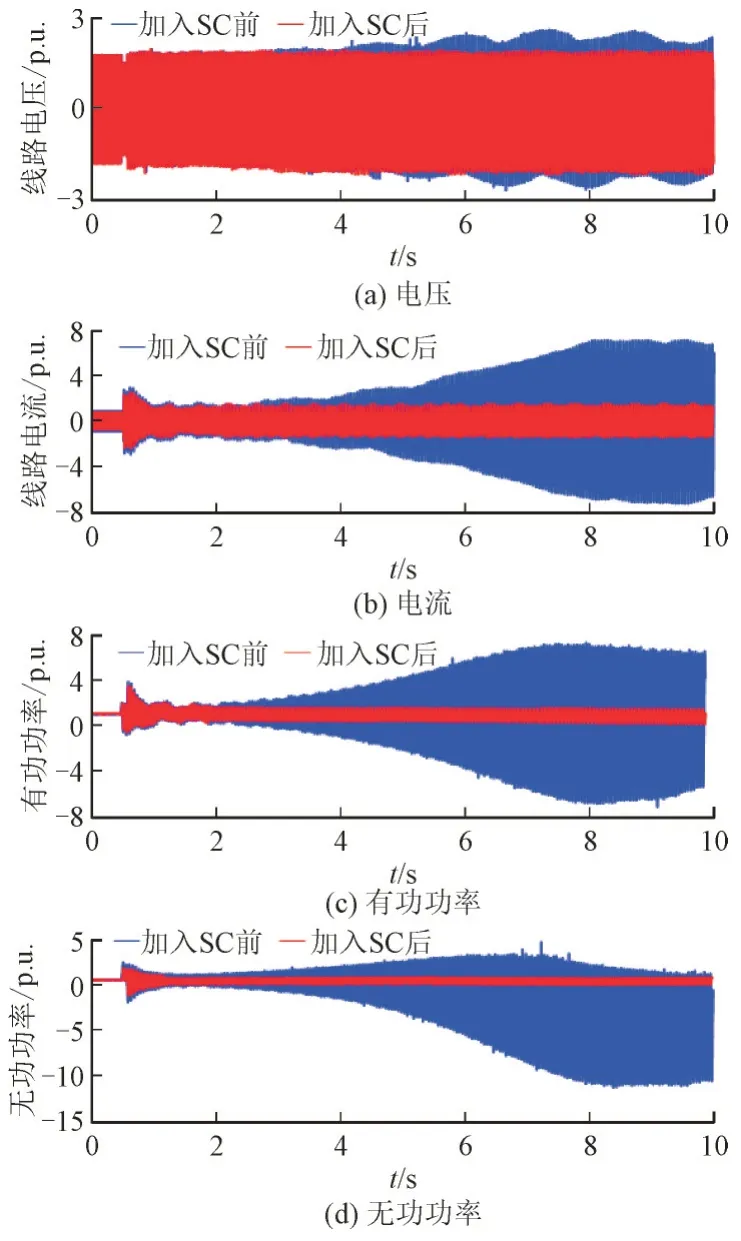
图8 SC加入前后IEEE第一标准型系统各参量波形Fig.8 Parameter waves of IEEE first standard system before and after SC addition

由图8 可知，IEEE 次同步振荡第一标准型系统加装同步调相机后，汇流母线并网电压和电流波动大幅降低；对系统提供了无功支撑，系统的有功功率和无功功率输出均得到很大程度的改善，保障了系统故障后快速恢复正常运行能力，有效抑制了振荡。

3.2 抑制光伏发电并网系统的SSO

搭建图1 光伏发电并网系统的仿真模型，主要参数如表1 所示。

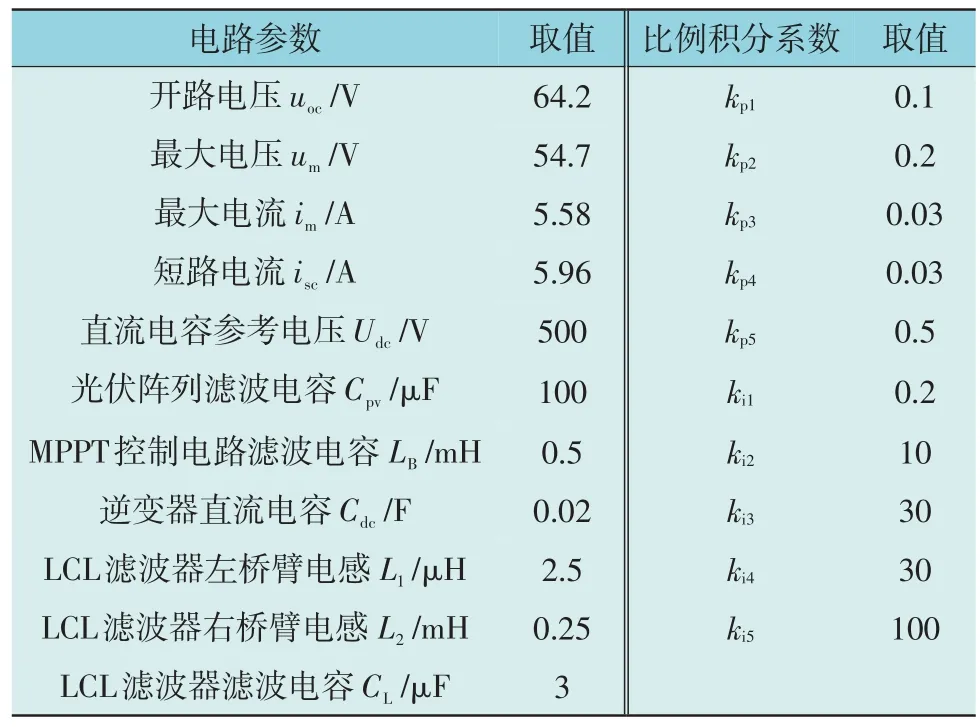
表1 仿真模型主要参数设置Table 1 Key system parameter settings

在光辐照度S=1 kW/m2、温度T为25℃的标准工况下，光伏阵列经DC-DC 升压变换、逆变、滤波、交流升压后，远距离输送后并入35 kV 电力系统。光伏发电场由100 台0.1 MW 发电单元构成，经100台逆变器并网，将其等值为1 台10 MW 阵列经逆变器接入电网。1 台300 Mvar 调相机与光伏发电并联连接于电网高压汇流母线处。

对比加入调相机前后系统并网参量变化，验证新一代同步调相机对光伏发电并网系统次同步振荡的抑制效果。加入调相机前，截取2～3 s 时段光伏发电并网系统振荡过程，系统并网参量波形如图9 所示。

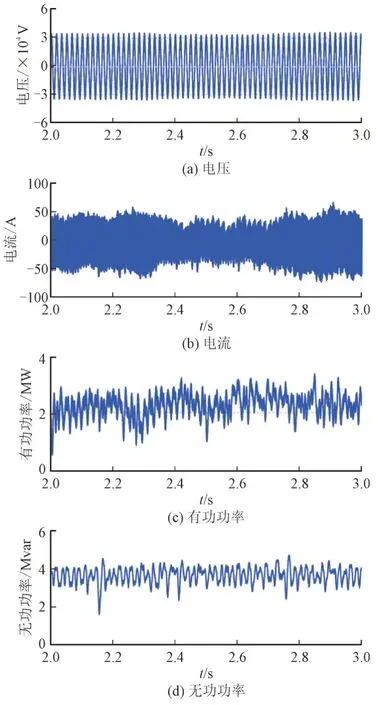
图9 系统并网参量波形Fig.9 Grid-connected parameter waves

由图9 可见，光伏发电并网系统各参量产生大幅波动，尤其是电流有较大畸变，致使并网有功大幅波动，系统稳定性差。

由模式分析法获得系统雅可比矩阵的特征值分布，如图10 所示。对比图10（a）和图10（b）可见，传统模型获得4 个负实根和1 对共轭复根，而精细化整体模型因其综合考虑了光伏电池、锁相环、滤波器、调相机等各环节，获得2 个负实根和7 对共轭复根，共轭复根是反映系统发生振荡的关键因素，因此精细化整体模型以更多的状态变量表征了更丰富的振荡模式信息。由图10（b）可知，有6 对共轭复根出现于复平面右半平面，对应的振荡频率及范围如表2 所示。

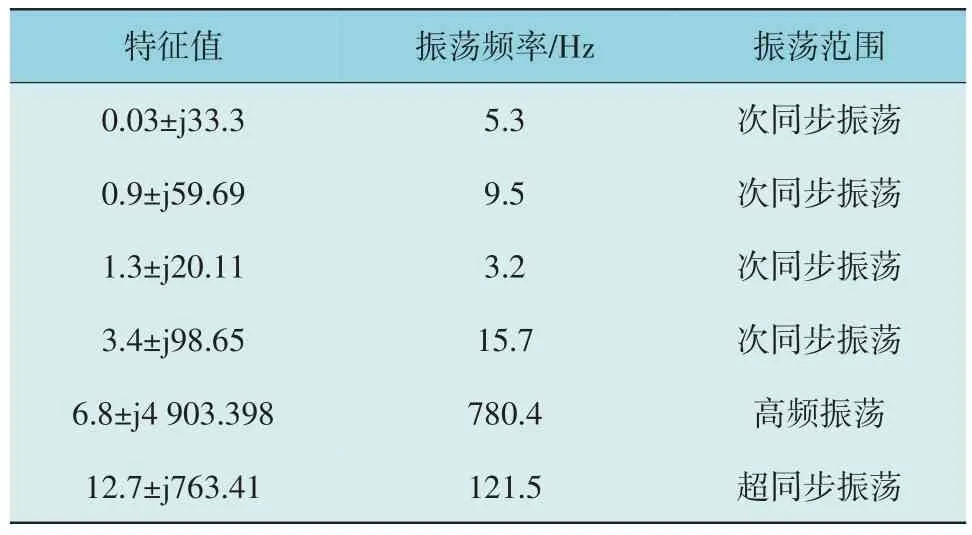
表2 右半平面特征值相关信息Table 2 Eigenvalues information of right half plane

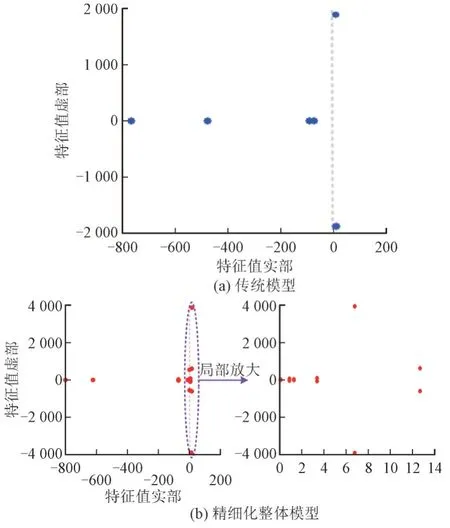
图10 系统雅可比矩阵特征值分布图Fig.10 Eigenvalue distribution diagram of system Jacobian matrix

无功补偿对于系统各频段振荡均有一定的影响[25]，加入调相机后，系统的并网参量波形及特征值分布如图11 和图12 所示。

图11 系统并网参量波形（SC加入后）Fig.11 Grid-connected parameter waves after SC addition

对比图11 和图9 可知，加入调相机后，系统并网的电能质量和稳定性大幅提升，并网电压保持稳定，大大提高了电压支撑强度，电流和有功振荡幅值大大减弱，电流幅值基本保持在基准值，在一定程度上提供了更大的有功支持。对比图12 和图10可知，系统发生振荡时，加入调相机后，系统特征根全部左移，原本处于右半平面的6 对特征值中有5对左移至左半平面，使得系统稳定性得到改善。仅振荡频率为780.4 Hz 的一对高频振荡特征根位于右半平面，且其虚部和实部幅值减小，向有利于稳定性的趋势发展。

综上，加入SC 后，使所有次同步振荡得到有效抑制，且对超同步振荡也有抑制作用。但是，在系统受到扰动时，调相机依据合成转矩提高系统稳定性的方式，其调节范围是有限的，难以实现将高频振荡范围等系统所有特征根彻底左移至左半平面。

4 结论

本文针对光伏发电并网引发的电力系统次同步振荡问题，进行数学建模与机理分析，研究基于新一代大容量同步调相机抑制次同步振荡的方法，有效抑制振荡，提升了系统稳定性，促进新能源消纳。得到以下结论：

1）综合考虑光伏电池、变换器、逆变器和同步调相机等电力系统各部分，建立光伏发电并网系统的精确化整体模型，与传统模型相比，能够以更丰富的振荡模式信息，为分析确定振荡引发主导因素提供更全面详尽的参考依据。

2）提出的基于模式分析法的调相机抑制电力系统次同步振荡方法，针对系统综合数学模型，求解其系数矩阵特征值及主导因子，由强相关状态变量准确定位引发系统振荡的潜在主导因素，能够依据lyapunov 稳定判据科学解释振荡机理进行，且能够很好地消除次同步振荡，提高光伏并网后的电能质量和系统阻尼，提高了系统稳定性。