基于VSC-HVDC的统一附加阻尼最优控制方法

张国华，刘心旸，刘卓锟，季一润，赵 媛，邓文军，杨大伟

（1.国家电网有限公司直流技术中心，北京 100052；2.国网冀北电力科学研究院，北京 100045；3.四川大学电气工程学院，成都 610065；4.国网冀北电力有限公司超高压分公司，北京 102488）

0 引言

电网互联是电力工业发展的必然趋势[1-3]，大规模互联电网可以降低整个电网的总备用容量，利用不同地区的时差和季节性差异来缓解负荷峰谷的波动，能够合理、经济地利用电力资源，降低成本[4]。

弱阻尼低频振荡（Low Frequency Oscillation，LFO）是目前大电网互联遇到的难题[5-7]。电力系统稳定器（Power System Stabilizer，PSS）是抑制低频振荡最简便的方法[8-10]。对实际电网而言，PSS 是增强系统阻尼、抑制系统低频振荡的首选方法[11]。文献[12]采用粒子群优化技术来确定PSS 参数的最优设置。文献[13]将电力系统稳定器参数的选择问题转化为基于特征值的多目标函数遗传算法求解的优化问题。文献[14]研究了多机电力系统中柔性交流输电系统功率振荡阻尼控制器和常规电力系统稳定器的协调整定。

研究发现，PSS 主要对发电机进行附加控制，但对于区域间振荡，其效果较差[15]。基于电网换相换流器的高压直流输电系统（Line Commutated Converter High Voltage Direct Current，LCC-HVDC）的附加阻尼控制成为交直流混合电网中的研究热点[16-18]。美国太平洋直流工程基于经典控制理论的频率响应法和根轨迹法设计直流附加阻尼控制器，有效抑制低频振荡[19-20]。文献[21]设计出针对不同振荡模式的多通道附加高压直流控制器。

LCC-HVDC 广泛用于附加阻尼控制，但与基于电压源换流器的高压直流输电系统（Voltage Source Converter High Voltage Direct Current，VSC-HVDC）相比，LCC-HVDC 通常存在换相失败问题。除HVDC外，柔性交流输电技术（Flexible Alternative Current Transmission Systems，FACTS）能够快速灵活地调节系统，从而有效增强系统的动态稳定性，尤其在对电力系统低频振荡及次同步振荡的抑制问题上[22]，其起到越来越大的作用。然而，FACTS 装置目前存在的最大问题就是造价很高，尤其是针对特高压电网的造价特别高，因此，出于经济性方面的考虑，FACTS 装置用来抑制电网的低频振荡应用范围还不广。一些学者开始通过VSC-HVDC 系统设计附加阻尼控制。文献[23]在VSC 中加入了附加控制器，并且为了抑制区域间振荡，采用了MLQG 方法来改善控制器的性能。文献[24]研究了虚拟同步机对电力系统低频振荡（Low Frequency Oscillation，LFO）的影响。目前，尽管在VSC-HVDC 领域已经进行了一些与附加阻尼控制相关的研究，但并没有专门考虑控制器的适应性。此外，大多数的阻尼控制是通过有功功率控制回路实现的，而没有考虑无功功率的控制。

文章提出了一种基于VSC-HVDC 的统一附加最优控制方式，通过总体最小二乘-旋转不变技术（Total Least Squares-Estimation On Signal Parameters Via Rotational Technique，TLS-ESPRIT）辨识系统降阶模型；根据得到的小信号模型，利用最优控制理论，设计了统一附加控制器，仿真分析与验证表明，所提控制方法相比于常规有功附加控制器具有更好的效果，且兼具鲁棒性。

1 VSC-HVDC 的结构和统一附加控制

用基于dq解耦的直接电流矢量控制的VSCHVDC 系统的控制框图如图1 所示。图1 中，Ps，Qs分别为交流侧有功、无功功率，Psref，Qsref为交流侧有功、无功功率参考值；Udc，Vac，Iac为直流电压、交流电压和交流电流，Udc_ref，Vac_ref为直流电压和交流电压参考值；id，iq为交流电流的d轴、q轴分量，idref，iqref为d轴、q轴电流分量参考值；ud，uq为交流电压的d轴、q轴分量；ω为角频率，L为交流侧等效电感；PI 为比例积分控制器。

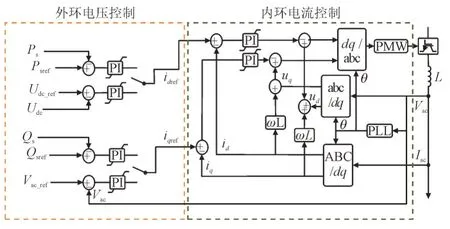
图1 VSC-HVDC的控制框图Fig.1 Control diagram of VSC-HVDC

1.1 外环电压控制

根据图1，外环电压控制由两部分组成，第一部分输出有功电流参考值idref，第二部分输出无功电流参考值iqref。idref由有功功率Ps及其参考值Psref的偏差决定，或由直流电压Udc及其参考值Udc_ref的偏差决定。同样，iqref由无功功率Qs及其参考值Qsref的偏差决定，或由交流电压Vac及其参考值Vac_ref的偏差决定。

通常，对于多端VSC-HVDC，总有1 台VSC 采用定直流电压控制，所以一般在定有功功率控制的VSC 中增设附加阻尼控制。所选的VSC 外环控制如图2 所示。图2 中，KP和KI分别为外环PI 的比例系数和积分系数；idlim，iqlim分别为d轴、q轴电流分量限值；s为复频率。

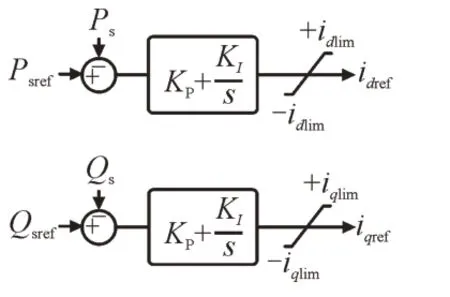
图2 外环功率控制框图Fig.2 Control diagrams of outer power control

1.2 内环电流控制

图3 为内环电流控制框图。

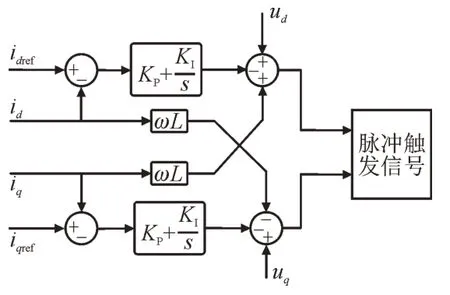
图3 内环电流控制框图Fig.3 Inner vector current control loop diagram

在d-q坐标下，VSC-HVDC 的系统模型可表示为：

式中：R，L分别为等效交流侧电阻和电感；Usd，Usq分别为三相桥臂差模电压d，q轴分量。

1.3 VSC的统一附加阻尼控制

VSC 的主控制决定其有功功率和无功功率，因此要实现交流系统的阻尼控制，除了主控制外，还需要增设附加控制。对于定功率控制的VSC，通常在其有功功率控制回路中加入附加控制，即在外环电压控制中增设附加控制。由于有功功率主要决定VSC 的阻尼特性，可以在定有功功率控制回路中设计VSC 的附加阻尼控制。另一方面，虽然无功功率对频率振荡的影响较小，但是其影响也不能忽视，由于无功功率可以改变电压特性，因此也可以利用无功来改善电网的阻尼特性。

考虑到VSC 的有功、无功控制可以通过d-q控制方案解耦，所以还可以在无功外环控制回路中设计无功附加阻尼控制，不仅可以提高VSC 的阻尼控制能力，还可以将控制范围从1 个通道扩展到2 个通道。由于利用了整个VSC 的视在容量，因此这种控制原理可以定义为一种统一附加阻尼控制方法，统一附加阻尼控制的控制框图如图4 所示。图4中，Padd，Qadd分别为附加有功、无功控制器输出信号。

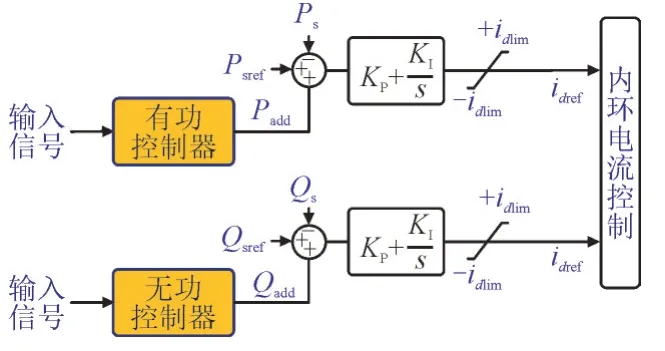
图4 VSC统一附加阻尼控制的控制框图Fig.4 Control diagrams of unified supplementary damping control for VSC

2 基于TLS-ESPRIT辨识的系统建模

2.1 系统建模方法

由于低频振荡总是发生在大规模并网电网中，所以文章研究的系统是交直流混合系统。图5 是附加控制与原系统的控制关系，在设计控制器之前，我们应当得到原系统模型，因此目前的关键问题是如何建立系统模型。

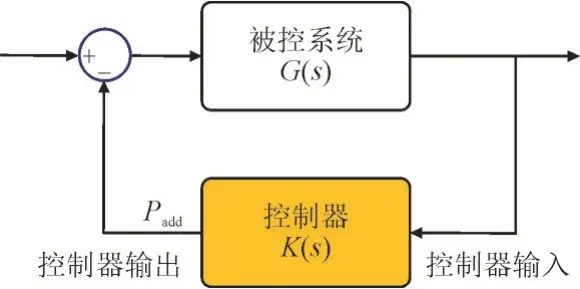
图5 附加控制与原系统的控制关系Fig.5 Relationship between the supplementary control and former system

建立电网系统模型的经典方法是对每个元件和设备进行建模，以便能够反映最准确的特性。然而，现代电力系统规模较大，很难应用于实际工程。还有一种应用广泛的方法是在不对具体部件建模的情况下对系统进行辨识，这种方法适用于小信号分析，因此文章采用TLS-ESPRIT 算法进行系统辨识。

2.2 基于TLS-ESPRIT算法的系统辨识

TLS-ESPRIT 算法是谐波分析和衰减正弦信号参数估计的有效手段，与传统算法相比，该算法抗噪声和抗干扰能力强，被广泛应用于信号处理。通常，采样信号可以表示为正弦信号和噪声的组合，其幅值呈指数衰减。采样时刻的表达式可以表示为:

式中：Ts为采样周期；p为信号实际含有的实正弦分量个数的2 倍；；ωk，ak，θk和σk分别为角频率、幅值、相角和衰减因子；ω(n)为白噪声。

由采样数据形成的Hankle 矩阵如式（5）所示，其中，L和M分别为矩阵的行数与列数；L>p，M>p，L+M-1=N，即N同为矩阵列数。

通过式（6）对式（5）进行奇异值分解：

式中：U为左乘正交矩阵；VH为V的共轭转置；M为对角阵，M的对角元素是按照大小排列的奇异值。

根据V按奇异值大小分为信号子空间VS和噪声子空间VN，VS的列向量是矩阵X的最大奇异值P对应的特征向量。通过删除矩阵VS的第一行和第二行，剩余矩阵分别为V1和V2。当不考虑噪声和干扰时，存在一个可逆矩阵Ψ[25]，使得

在考虑噪声和干扰时，式（7）可以改写为：

式中：e1,e2分别为V1与V2的误差矩阵。

根据Ψ可以得到信号参数，从而采用TLS 算法对Ψ进行优化并最小化误差矩阵D=[e1,e2]的范数，然后对矩阵[V1，V2]进行奇异值分解，得到：

其中M∈C2P×2P，可改写为：

最后，通过计算矩阵M的特征值λk(k=1,2,…,P)，可以得到各分量的角频率ωk、衰减因子σk和阻尼比ζk，其表达式如式（11）-式（13）所示。

对于N点，其采样信号Y=λc，其中

利用最小二乘法获得方程c=(λTλ)-1λTY的解，就可以得到信号中各分量cp的幅值ap和相位ϕp，如下所示：

3 基于辨识的最优控制器设计

对系统建模之后，需要设计性能良好的阻尼控制器，文章采用了最优控制理论对控制器进行设计。

考虑如下系统：

确定最佳控制向量的矩阵K，使得性能指标J达到极小。

式中：Q为正定（或半正定）埃尔米特矩阵或实对称矩阵；R为正定埃尔米特矩阵或实对称矩阵；t为时间。

将u=-Kx代入式（20）可得：

经过一系列化简可得：

式中：P为正定埃尔米特矩阵或实对称阵；T为非奇异矩阵。

若xT[TK-(TT)-1BTP]T[TK-(TT)-1BTP]x取最小值，则J取得最小值。因此可得：

通过解里卡蒂方程ATP+PA-PBR-1BTP+Q=0 即可获得矩阵P，并得到最终控制器，如图6 所示。

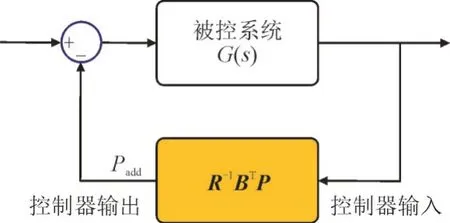
图6 最优控制框图Fig.6 Optimal control diagram

4 算例分析

对如图7 所示的交直流混合系统进行仿真分析。该系统为一个8 机2 区系统，其中VSC-HVDC和交流线路将2 个区域连接在一起。

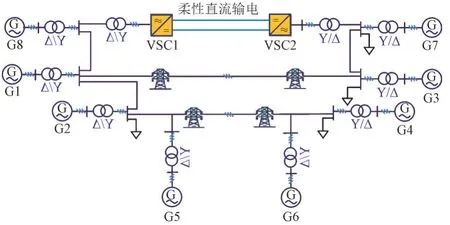
图7 交直流混合系统Fig.7 AC-DC hybrid system

4.1 系统辨识

要设计统一最优控制器，首先要对原系统进行辨识建模。根据分析，选择最优控制器的反馈信号为ω3，即G3 的转子转速。被辨识系统的有功控制回路的传递函数GP_system如式（24）所示，并且实际曲线与辨识曲线的比较如图8 所示，可以看出2 条曲线的吻合程度较高，这验证了TLS-ESPRIT 算法的正确性。

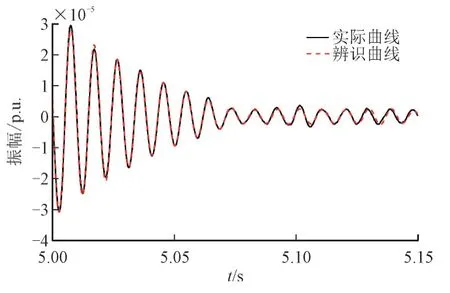
图8 有功控制系统GP_system的辨识结果Fig.8 Identified results of active power-controlled system GP_system

同样地，被辨识系统的无功控制回路的传递函数GQ_system如式（25）所示，图9 所示为实际曲线与辨识曲线的对比，可以看到2 条曲线吻合程度较高，进一步证明了TLS-ESPRIT 算法的正确性。

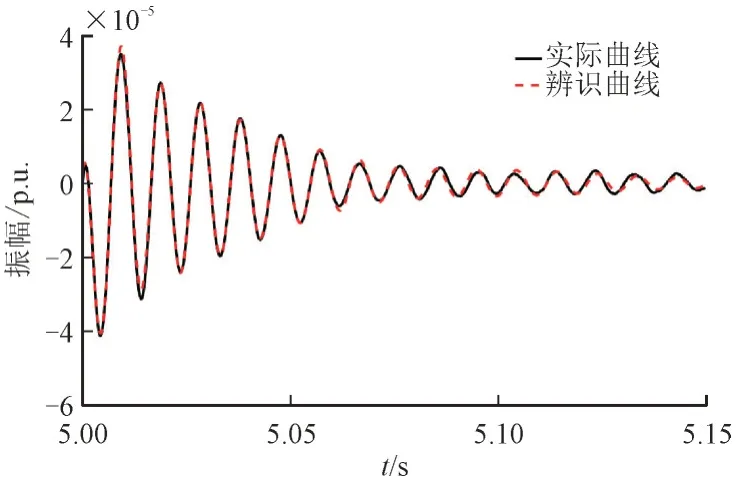
图9 无功控制系统GQ_system的辨识结果Fig.9 Identified results of reactive power-controlled system GQ_system

4.2 最优控制器设计

根据最优控制理论得到控制器表达式并进行降阶，其中有功和无功控制回路的降阶最优控制器KP_system(s)，KQ_system(s)分别如式（26）和式（27）所示，降阶前后控制器的波特图如图10 和图11 所示。

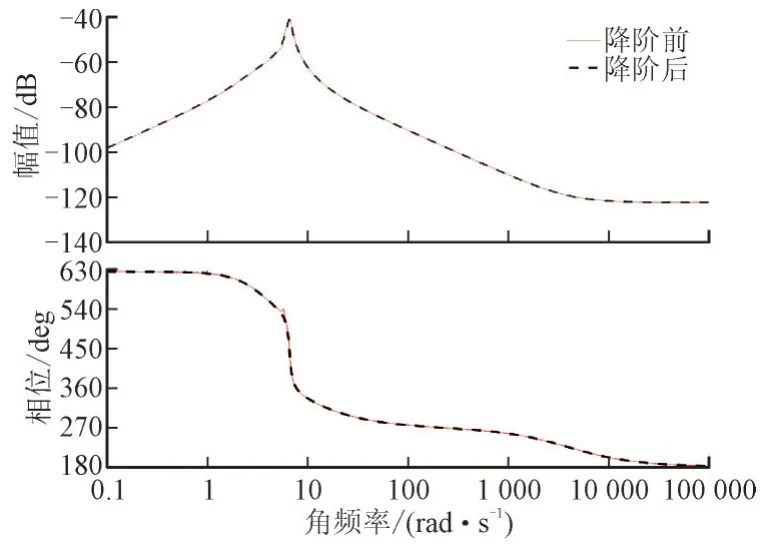
图10 控制器KP_system（s）降阶前后波特图Fig.10 Controllers KP_system（s）with and without reduction

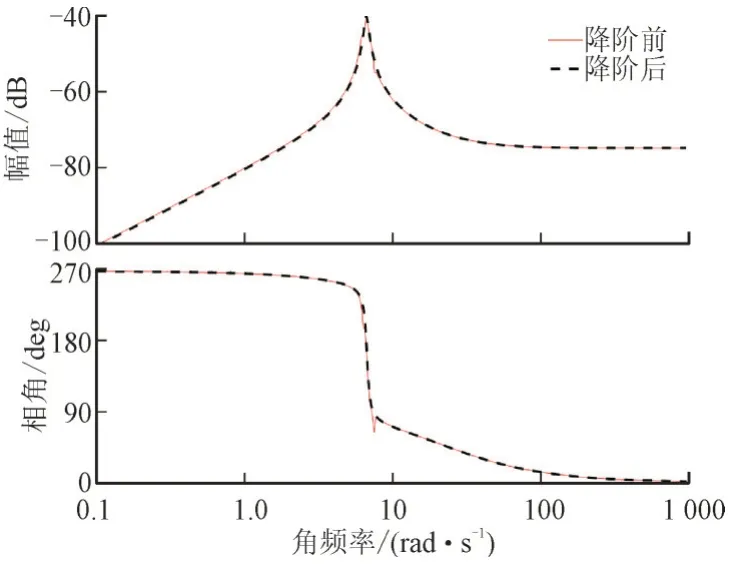
图11 控制器KQ_system（s）降阶前后波特图Fig.11 Controllers KQ_system（s）with and without reduction

4.3 仿真验证

将设计的统一最优控制器加入到如图7 所示的八机两区系统中，并在每种仿真情况下给出仅采用有功附加控制的控制效果图，以对比验证统一最优控制器的有效性。

4.3.1 负载扰动

负载扰动情况下设置2 s 时VSC2 处的负载突然减小，在不同的控制策略下比较系统的运行情况。图12 和图13 给出了发电机的转速、有功功率以及和VSC-HVDC 的有功功率和无功功率。

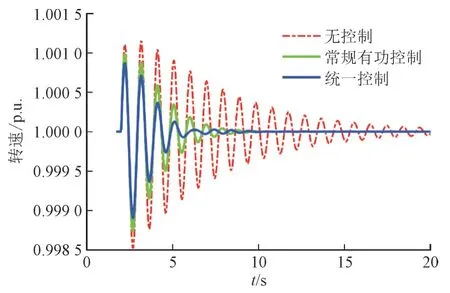
图12 负载扰动时不同控制策略下G3的转速Fig.12 Rotor speeds of G3 with different schemes during load disturbance

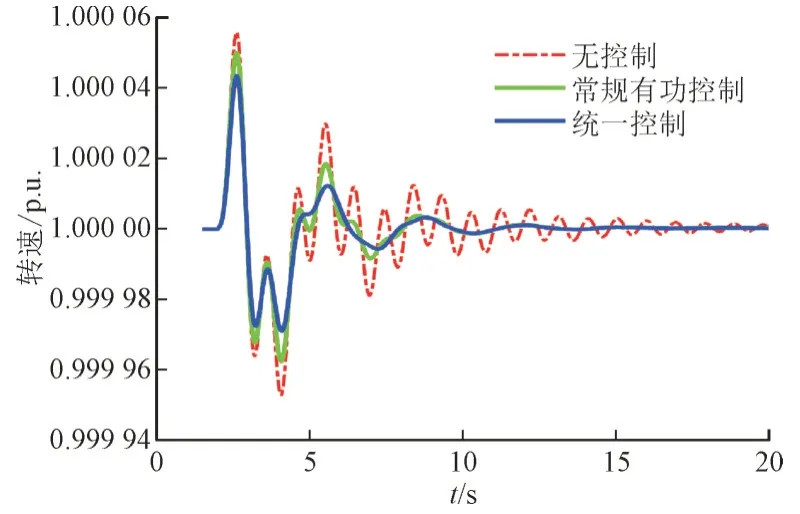
图13 负载扰动时不同控制策略下G6的转速Fig.13 Rotor speeds of G6 with different schemes during load disturbance

从图12 和图13 可以看出，统一最优控制的效果较好，提高了系统的阻尼比。根据计算结果，在常规有功控制的情况下，原振荡模式的阻尼比由2.73%提升至7.12%，在统一控制加入后，阻尼比提升至9.59%，证明了无功控制也有助于阻尼的提高。

4.3.2 单相接地故障情况

故障情况下，设置在2 s 时发生单相接地故障，并在不同的控制策略下比较系统的运行情况，如图14 和图15 所示，仿真结果证明了统一控制器的有效性。根据计算结果，单相接地后，在常规有功控制的情况下，原振荡模式的阻尼比由2.53%提升至5.72%，在统一控制加入后，阻尼比提升至7.11%，同样证明了无功控制也有助于阻尼的提高。

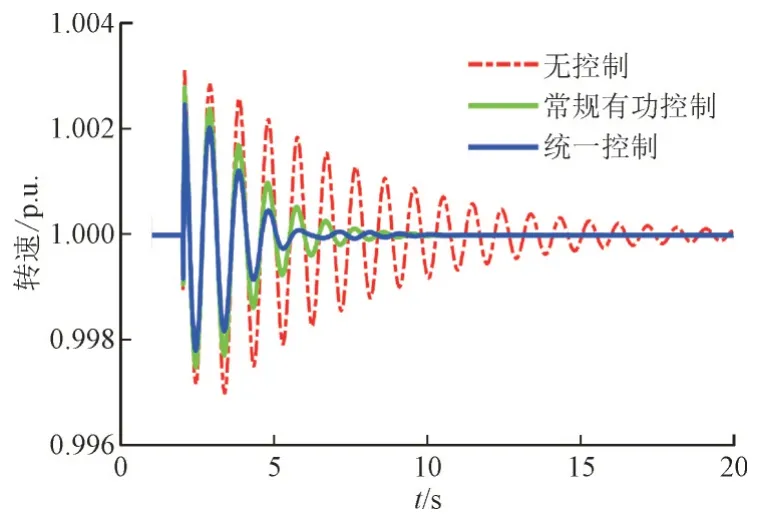
图14 单相接地故障时不同控制策略下G3的转速Fig.14 Rotor speeds of G3 with different schemes during single-phase ground fault

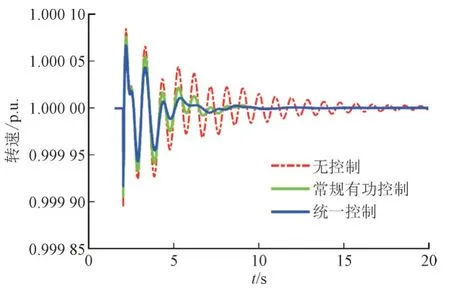
图15 单相接地故障时不同控制策略下G6的转速Fig.15 Rotor speeds of G6 with different schemes during single-phase ground fault

4.3.3 三相接地故障情况

故障情况下，设置在2 s 时发生三相接地故障，并在不同的控制策略下比较系统的运行情况，如图16 和图17 所示，仿真结果证明了统一控制器在三相故障情况下也具有较好的控制效果。

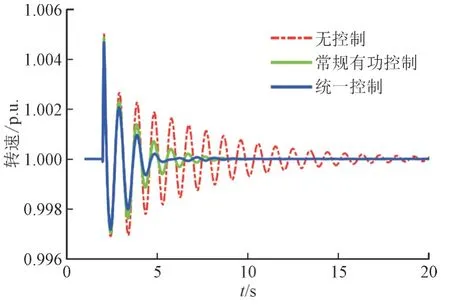
图16 三相接地故障时不同控制策略下G3的转速Fig.16 Rotor speeds of G3 with different schemes during three-phase ground fault

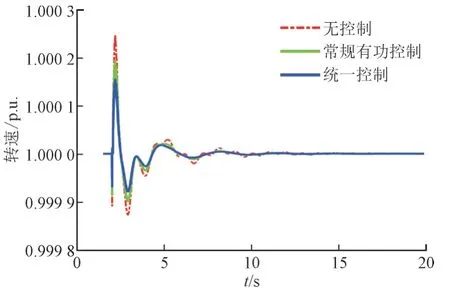
图17 三相接地故障时不同控制策略下G6的转速Fig.17 Rotor speeds of G6 with different schemes during three-phase ground fault

4.3.4 运行方式改变

为了进一步验证统一控制器的鲁棒性，2 s 时改变VSC 的运行方式，VSC 的输出从额定的400 MW降低到50 MW，并在不同的控制策略下比较系统的运行情况。图18 和图19 给出了仿真结果，可以看到统一控制器仍然能抑制振荡，验证了统一控制器具有良好的鲁棒性。

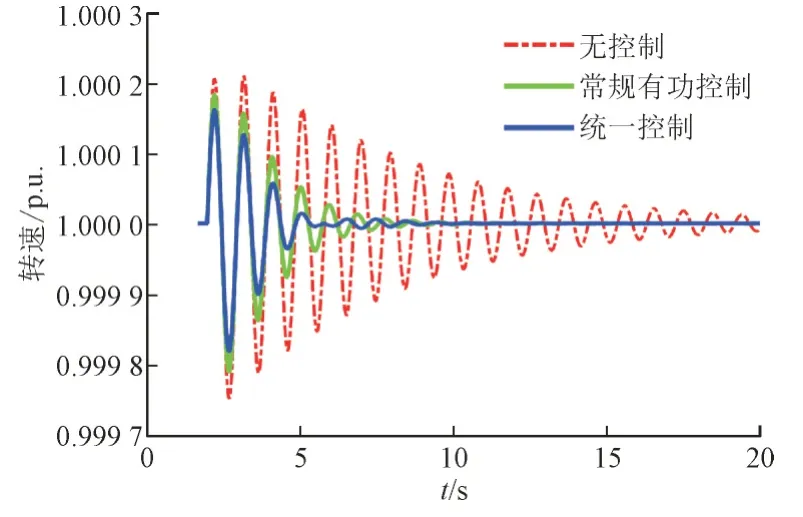
图18 运行方式改变时不同控制策略下G3的转速Fig.18 Rotor speeds of G3 with different schemes when operating mode is changed

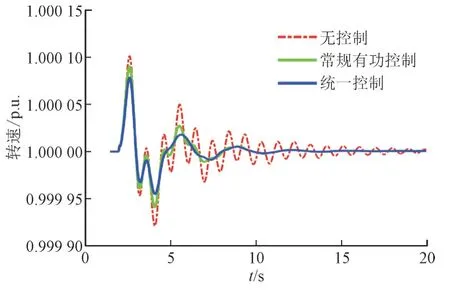
图19 运行方式改变时不同控制策略下G6的转速Fig.19 Rotor speeds of G6 with different schemes when operating mode is changed

4.3.5 断线故障

为了进一步验证统一控制器的鲁棒性，2 s 时切除G6，且其相连的交流联络线发生断线故障，在不同的控制策略下比较系统的运行情况。图20 和图21 给出了仿真结果，可以看到统一控制器在系统拓扑结构变化后仍然能抑制发电机3 的低频振荡，（其中G6 因与系统断开，有无控制均不影响其运行，不作为对比研究对象），验证了统一控制器具有良好的鲁棒性。

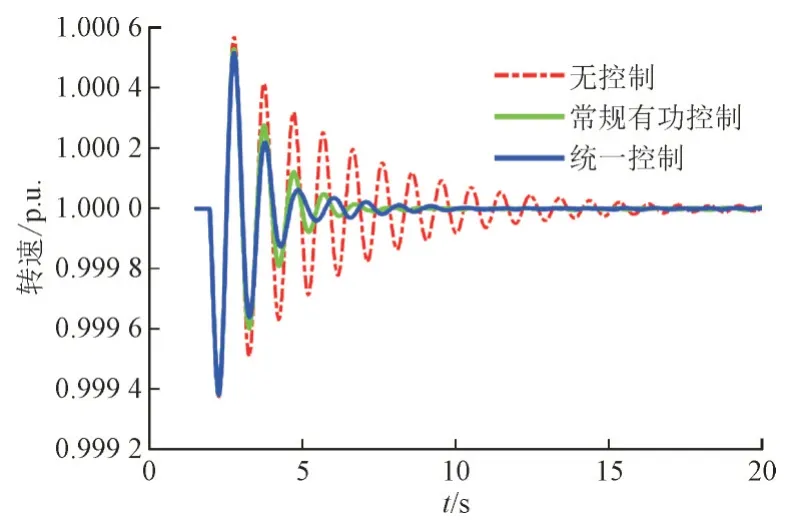
图20 断线故障时不同控制策略下G3的转速Fig.20 Rotor speeds of G3 with different schemes during wire break fault

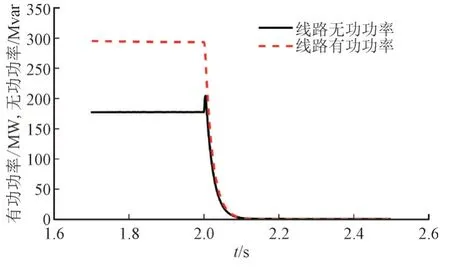
图21 断线前后交流线路有功无功Fig.21 Active power and reactive power of AC line before and after line break fault

5 结论

文章设计了基于VSC-HVDC 抑制低频振荡的统一附加阻尼控制器，得出以下结论：

1）VSC 的有功和无功控制回路均可用于低频振荡的抑制。由于VSC 的dq解耦控制，无功附加阻尼控制器可独立于传统的有功阻尼控制器，扩展了VSC-HVDC 的控制维度。

2）与传统的有功阻尼控制器相比，通过VSC 抑制低频振荡的效果更好，其原因是VSC 相当于有2个控制器同时抑制振荡。

3）基于最优控制理论和TLS-ESPRIT 算法设计的最优控制器能够有效地抑制低频振荡，并且无论是在故障、电力干扰还是其他情况下，低频振荡都能被快速消除。