数形结合思想在小学数学“解决问题”教学中的运用和思考

赵庆艳

数形结合思想是小学阶段最常见的一种数学思想方法。无论是解决问题、学习新知识，还是做练习题，数形结合都是解决问题的“钥匙”，它可以将复杂的问题简单化，让学生的思路更加清晰明了。笔者认为，小学数学教师在教学中应重视数形结合思想的运用，并通过实践将数形结合思想进行总结和升华，这样才能更好地培养学生的数学思维，提高学生的数学能力。在本文中，笔者从个人的角度出发，谈谈数形结合思想在小学数学“解决问题”教学中的运用，提出一些思考，以供参考。

一、目前存在的问题

基于数形结合思想，教师在教学过程中会让学生先根据题意画出图形，然后根据图形引导学生分析题意。但是笔者在教学过程中发现，部分学生的作图能力不强。如有的学生画出的线段图不规范，不能够准确表达题意；有的学生没有做到数形一一对应，对于数在图中指的是哪一部分、图中的每一部分表示的是算式中的哪一个数等问题，他们不是完全清楚。除此以外，部分教师在教学过程中很少渗透数形结合思想，对运用画图解析题意的方法不够重视。

二、小学数学“解决问题”教学中运用数形结合思想的思路

针对以上存在的问题，笔者认为，小学数学教师在运用数形结合思想开展“解决问题”教學时应做到以下三点。

（一）挖掘教材内涵，提炼数形结合思想

在小学数学教学中，教师要吃透教材，研究教参。在讲解新的知识点时，教师应渗透数形结合思想，让学生从心底接纳数形结合思想，并运用到解决问题的过程中。教师在教学过程中要挖掘教材内涵，由浅入深地培养学生的数形结合思想，引导学生理解数与形之间的关系，实现数与形的一一对应，使抽象的知识变得清晰、具体，让数学学习更直观。

（二）关注隐性目标，渗透数学结合思想

《义务教育数学课程标准（2022年版）》指出，通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的基础知识、基本技能、基本思想、基本活动经验。其中，基础知识和基本技能是显性的教学目标，基本思想和基本活动经验是隐性的教学目标。在新课标背景下，教师制定教学目标时不仅要强调显性目标，还要挖掘隐性目标。小学数学教师要提高对数形结合思想的重视度，在教学中渗透数形结合思想，并将其纳入“解决问题”教学目标，使数形结合思想的指向性更强，以增强数学课堂教学效果。

（三）分析教学环节，落实数形结合思想

教师要以数形结合思想为指导，提高小学数学教学水平。基于此，教师应主动开展课例研究，不断提升自身的专业素养。在开展课例研究的时候，教师要从如何引导学生通过“形”分析问题、数与形是怎样结合这两方面进行观察和分析。教师在每一次听完课例后应进行说课，针对每一个教学环节说出自己的教学目标，并就没有达成的目标认真分析原因。例如，“形”是帮助分析数量关系的，但有时“形”并没有起到分析题意的作用，教师就应思考其原因是什么。教师通过分析教学环节，能够总结经验，找出不足，从而使数形结合的教学思想真正落实到课堂中。

三、小学数学“解决问题”教学中运用数形结合思想的几点思考

（一）增强渗透数形结合思想的意识

笔者认为，从小学低段到高段，教师无论教哪个年级，都应有意识地在课堂教学中渗透数形结合的思想和方法。纵观小学阶段的数学教学，无论是认识数字，还是算理课、概念课、统计课的教学，教师都可以以数形结合的思想来帮助学生理解知识，降低学生学习的难度。例如，在教学一年级上册“重叠问题”单元的相关内容时，教师可以先提出问题“一只大雁从前面数排在第6位，从后面数排在第3位，请问这行大雁一共有多少只”，并引导学生通过画图的方式去分析问题、回答问题。然后，教师可以讲解加减法运算方法，展示用加法进行计算的“6+3=9（只）”，让学生理解为什么这样列式，并展示用减法计算的“9-1=8（只）”，让学生明白这样计算的理由。最后，教师可以让学生对比画图法和加减法运算这两种方法哪种更好。这样能在比较中突出画图方法的优势，能使数形一一对应，学生会感觉到画图更直观。除此以外，笔者认为，教师在教学中可以从以下两个方面渗透数形结合思想。

1.运用数形结合思想，在“解决问题”教学中帮助学生搭建数学模型。“解决问题”教学一直是小学数学教学的一个难点，在教学中，有时笔者刚讲的题学生明明懂了，但是遇到另一道类似题目他们又不会了。后来，笔者通过观摩学习骨干教师讲课，感到自己的课堂教学策略需要充实和改进的地方太多了。笔者反思了自己的教学策略：每当遇到“解决问题”教学时，总是让学生先认真读题，再让学生说一说题目中告诉了我们什么、让我们求的是什么、该怎样解决，最后让学生列式解答，这种教学方法没有给学生足够的自主学习空间，学生没有经历“应用问题”数学模型的形成过程，因此对相关知识只知其然，而不知其所以然。后来，笔者利用数形结合思想，帮助学生构建“解决问题”数学模型，教学效率大大提高，学生对相关知识的理解也更加直观和透彻。其实，小学数学的教学，从低段到高段，自始至终就没有离开过数学模型思想，从自然数的认识，到数学中的概念、性质，再到面积公式、体积公式的推导和数量关系式的建立等，都蕴含着数学模型思想，而这些数学模型的搭建又离不开数形结合思想。以植树问题为例，教师指导学生画线段图并在此基础上进行观察比较，可以使学生充分体验数学模型“棵数=间隔数+1”的形成过程。另外，“路程=速度×时间”“总价=单价×数量”等数量关系式的建立，也是在充分借助图形的基础上归纳总结出来的。

2.运用数形结合思想，在“解决问题”教学中帮助学生理解数量代换。数量代换在“解决问题”教学中经常会用到，它可以使问题简单化，从而帮助学生更高效地解决问题。以青岛版小学数学一年级下册第一单元“逛公园——20以内的退位减法”中的问题“求一个数比另一个数多几或少几”为例，该问题能促进学生对减法意义的深入思考，其具体问题是：“二班比一班多捡了几个易拉罐，怎样列式？为什么二班的数量要减去一班的数量？”在解决问题的过程中，学生运用数形结合思想，通过摆一摆和画一画的方式，可以理解为什么用减法来计算。但是笔者通过观察图片发现，该问题可以转化成“整体和部分”之间的关系，这能使学生更容易理解题意、解决问题。从该教材的配图中可以看出，二班分成了两部分，一是与一班同样多的部分，二是比一班多出来的部分，这样可以让学生更容易理解“15-10”，知道这里的“10”就是与一班同样多的部分。在这个过程中，学生能体验数量代换在解决问题中的应用，进一步加深对数形结合思想的理解。

（二）形成“解决问题”教学的思路和方法

1.帮助学生理解题意。笔者在教学中发现，要想让“形”很好地帮助学生分析题意，就要先使学生理解题目中的关键词语，并在理解题意的基础上通过“形”使抽象的题意变得直观起来。如有一道题是这样的：“在全长1000米的小路一边植树，每隔5米栽1棵（两端要栽），一共需要多少棵树苗？”在教学过程中，笔者先借助课件或教具让学生充分理解“一边植树”“两端都栽”“每隔5米栽1棵”的确切含义，帮助学生透彻理解题意，这样学生才知道如何画图。又如，在教学“不规则物体的体积”相关内容时，有一道练习题是这样的：“在一个长8米、宽5米、高2米的水池中注满水，然后把两根长3米、宽2米、高4米的长方体石柱豎着放入池中，水池中溢出的水的体积是多少？”笔者先让学生独立思考，然后让学生说一说解题思路。一名学生说：“两根石柱的体积有多大，溢出的水体积就有多少。”笔者对该学生投去了赞许的目光，但这时另一名学生站起来说：“我不认同，因为水池的高度只有2米，而石柱的高度有4米，所以露在外面的石柱没有占用水池中水的空间。”这两种答案中哪一种答案是正确的呢？为了帮助学生理解题意，笔者以画图的方式，根据题意在黑板上形象直观地把这道题呈现了出来，让学生明确了哪一部分石柱是浸在水里的，哪一部分石柱是露在水面以外的。笔者通过画图的方式，将抽象的数量关系形象直观地展现出来，帮助学生更好地理解了题意。

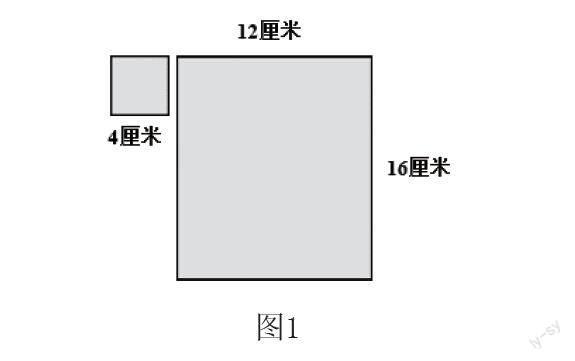
2.引导学生画图。在学习数学的过程中，画图有益于学生分析问题、解决问题。比如，笔者在教学“最大公因数的应用”相关内容时，发现这样一道题目：“储藏室长16分米，宽12分米，如果用边长是整分米的正方形地砖把储藏室的地面铺满，可以选择边长是几分米的地砖？边长最大是几分米？”读题后，有的学生向笔者投来了疑惑的目光，很显然他们没有理解题意。于是，笔者先用课件直观展示题目，帮助学生审题，使学生明确了题意。接着，笔者给每个学生发了一张长16厘米、宽12厘米的长方形纸（图1），引导学生在纸上画一画，然后用投影仪展示。通过投影仪的直观展示，学生发现该题中正方形地砖的边长可以是1分米、2分米、3分米或4分米。

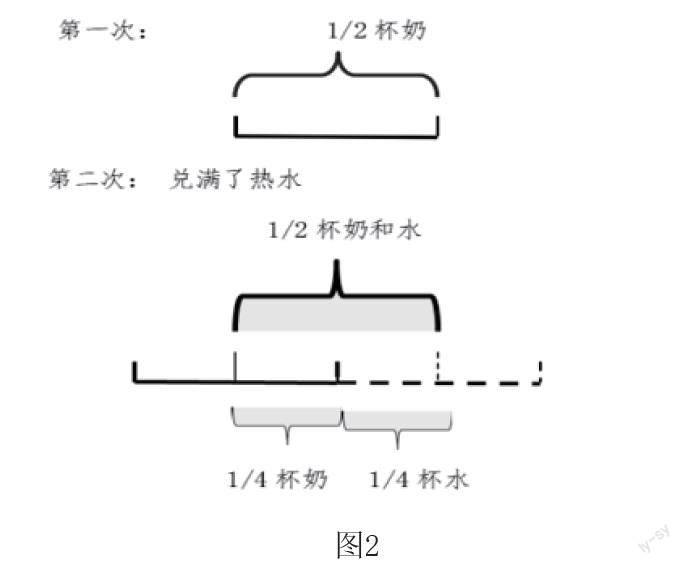
又如，在教学“分数加减混合运算”时，笔者利用课件展示题目：“一杯纯牛奶，乐乐喝了半杯后，觉得有些凉，就兑满了热水，接着他又喝了半杯，就出去玩了。乐乐一共喝了多少杯纯牛奶？多少杯水？”接着，笔者先让学生独立思考，然后写出算式。但是几分钟过去了，除了个别学生拿起笔列算式，大多数学生都皱起了眉头。见此情形，笔者开始思考“这道题对学生来说是不是难度太大，应该怎样引导学生呢？”这时，笔者想到了画线段图的方式，于是让学生在练习本上根据自己的理解画图。在笔者的引导下，学生受到启发，他们纷纷拿起笔在纸上画线段图，用数形结合的思想分析题意、解决问题。有的学生是这样画的（见图2），笔者觉得简单明了，而且非常准确。

结语

在小学数学“解决问题”教学中，图示的直观性、形象性是教师的任何语言都代替不了的，教师要在教学中让学生养成画图的习惯，运用数形结合思想帮助学生理解数学概念、寻找解题思路。笔者认为，运用数形结合思想，应成为小学数学教师教学的一项基本功，也应成为学生学习数学的一项基本能力。

（作者单位：山东省东营市东营区瀚文小学）