巧用几何直观 助力数学理解

【摘  要】小学生的思维以具体形象思维为主，理解抽象的数学知识经常需要借助直观的感性材料，在具体的学习情境中进行有效的数学学习探究。几何直观是一种重要的数学素养，其突出优势是化抽象为形象，展现问题的本质，搭建沟通感性与理性的桥梁，降低学习难度，从而促进学生的数学理解与问题解决，提升学生的数学素养。基于几何直观在小学数学教学中的重要地位，本文旨在从以下三个方面阐述几何直观在数学教学中的运用探究，希望对实际教学有所帮助。

【关键词】小学数学；几何直观；数学理解；问题解决

《义务教育数学课程标准（2022年版）》（以下简称《课标》）指出，几何直观主要是指运用图表描述和分析问题的意识与习惯。几何直观有助于把握问题的本质，明晰思维的路径。对学生而言，几何直观是一种有效的学习方法，在数学学习过程中发挥着重要的作用；对教师而言，几何直观是一种有效的教学手段，是落实培养学生核心素养的有效举措。

一、借助几何直观，验证数学猜想

猜想是不知其真假的数学叙述，也是学生喜爱的一种学习方式。它可以激发学生的学习热情，引发验证、求知的心理需要。涉及“图形与几何”相关知识的猜想，教师经常会引导学生通过画一画、剪一剪、拼一拼等多种形式的数学活动，充分调动学生的手、脑、眼多个器官的协调配合，经历“做”数学的学习过程，利用几何图形的形象直观，用图形说话，验证数学猜想，从而丰富学生脑中的图形表象，提升对图形的认识，发展空间观念，为后续学习做好知识铺垫。

例如，教学“圆柱的侧面展开图”时，教师请学生猜一猜：圆柱的侧面展开可能是什么图形？“长方形”“正方形”“不规则图形”“梯形”……教师对于学生的多种猜想，并不急于进行评判，而是鼓励学生动手剪一剪带来的圆柱侧面学具，验证自己的想法是否正确，再和小组成员交流。

师：你是怎么剪开圆柱侧面的，圆柱侧面展开是一个什么图形？你的猜想是对的吗？

生1：我是沿着圆柱的一条高剪的，圆柱的侧面展开是一个长方形，长方形的长等于圆柱的底面周长，宽等于圆柱的高，和我原来想的一样。

生2：我也是沿着圆柱的高剪的，但是我得到的是一个正方形。我发现这个圆柱的底面周长和高相等。

师：还有不同的剪法吗？

生3：如果沿着斜线剪开，圆柱侧面展开是一个平行四边形。

生4：我也是这么剪的。而且我还发现了，平行四边形的底等于圆柱的底面周长，高等于圆柱的高。

生5：我得到的是不规则图形，我是任意弯弯曲曲剪的。

师：同学们的想法、做法都非常棒！可是为什么你们都没提到梯形呢？

生6：因为“只有一组对边平行的四边形叫作梯形”。我是这么想的，不管怎么剪，圆柱的侧面展开都不可能是梯形。就算得到的是一个不规则图形，我们也可以再通过剪、移、拼的方法，把不规则图形转化成长方形。

师（竖起大拇指）：大家听明白了吗？想不想验证他的猜想对不对呢？

一石激起千层浪，学生的学习激情被再次点燃，大家又兴致勃勃地动手剪了起来，再次开启数学学习之旅。

又如，教学“三角形的内角和”时，由于学生在平时使用三角尺的操作实践中，经历量角的过程，认识到特殊的直角三角形的内角和是180°。因此，学生会基于已有的知识经验进行合理、有根据的数学猜想：三角形的内角和是180°。教师肯定学生的想法后，提出问题：“那你要用什么方法验证任意三角形的内角和是180°呢？”“三角形的个数是无限的，需要验证哪些三角形的内角和，才能代表所有三角形的内角和呢？”学生已经学习了三角形的分类，一致达成共识，选取锐角三角形、直角三角形、钝角三角形进行分工操作探究。刚开始，多数学生用量一量、算一算的方法，发现得出的数据有时会存在偏差，比180°大些或小些，意识到用度量的方法验证，得到的结果不统一。这时，教师启发学生：“180°是什么角？能不能找到比度量更精确的验证方法呢？”问题驱动思考，直观的学习材料丰富了学生的想象空间，为学生提供了不同的思维路径。有的学生分别撕或剪下三角形的三个内角，拼成平角；有的学生通过折一折，把三角形的三个内角拼成平角。学生在动手操作、直观体验、交流表达的活动中，不断积累数学活动经验，自主探索数学规律，经历数学“再发现”的过程，感受成功的喜悦和学习的快乐，增强了学习自信心。

二、依托几何直观，感悟数学思想

隐性的数学思想方法蕴涵于数学知识体系中，数学思想方法是形成学生良好认知结构的纽带，是由知识转化为能力的桥梁。依托几何直观，可以让无形的数学思想“显形”，变得具体化、生动化、形象化，激发学生的学习热情，促进学生的主动理解，自觉建构新知体系。

在教学“植树问题”时，出示：同学们在全长20米的小路一边植树，每隔5米栽一棵，一共要栽多少棵树？学生通过画线段图、列式计算，自主探索植树问题的三种情况：两端都栽，棵数=间隔数＋1；两端都不栽，棵数=间隔数-1；只栽一端，棵数=间隔数。但课后练习的反馈情况暴露出学生并未能真正理解“植树问题模型”，无法正确运用“间隔数加1”“间隔数减1”“棵数等于间隔数”解决实际问题。究其原因是课堂上教师关注了学生的活动体验，却忽视了结合直观引导学生理解“都是求棵数，为什么要加1，减1或不加不减的数学本质”。所以，教师在教学过程中要引导学生观察直观图（如图1～3），充分借助直观图上的点（树）和段（间隔），采用手指比划、画箭号等直观学习方法，建立棵数与间隔数之间的一一对应关系，理清知识间的内在联系，促进学生对知识的本质理解，建构清晰完整的数学模型，进而能综合运用所学知识灵活、正确地解决问题。

教学“平行与垂直”，让学生展开想象：把一张纸想象成一个无限大的平面，然后把想象的两条直线的位置关系画在纸上。教师收集代表性作品，标上序号。“你们能给这些直线进行分类吗？”学生通过观察，进行第一次分类，直观地根据“两条直线表面有无交叉”分成两类。“直线有什么特点呢？”“直线没有端点，可以向两端无限延长。”在教师的启发下，学生通过画延长线，发现有些没有交叉的两条直线，画延长线后可以相交于一点；而有一些是无论怎么延长都不会相交，经历第二次分类：同一平面内，两条直线的位置关系存在“相交和不相交”兩种情况。教师顺势引导学生学习“平行”的概念。紧接着教师又问：“这些相交的直线还可以进行分类吗？”学生通过议一议、量一量，进行第三次分类发现：两条直线相交的角，可以分为直角和不是直角两类。此时进行“互相垂直”概念的学习水到渠成。借助直观材料的感性支撑，学生经历“剥笋式”的分类学习探究过程，不仅理清了同一平面内两条直线的位置关系，逐步抽象出数学概念，还学会了运用分类的数学思想发现、分析、解决问题。

三、活用几何直观，解析数量关系

徐利治先生指出：“几何直观是借助于见到的或想到的几何图形的形象关系，产生对数量关系的直接感知。”鉴于小学生的心理认知和思维水平，纯文字呈现的问题，对他们而言，有时显得抽象难懂，很难凭文字信息直接理解数量关系，不知从何入手思考问题，思路不清，解题不畅。如何突破这一“瓶颈”呢？在解决问题的过程中，教师应培养学生在理解题意的基础上，养成自觉画图、分析思考的学习习惯，借助图形理解数量关系，把复杂的数学问题简单化，勾连已知和未知之间的通道，寻求解决问题的突破口，探索解决问题的思路，提高学生的数学思维水平。

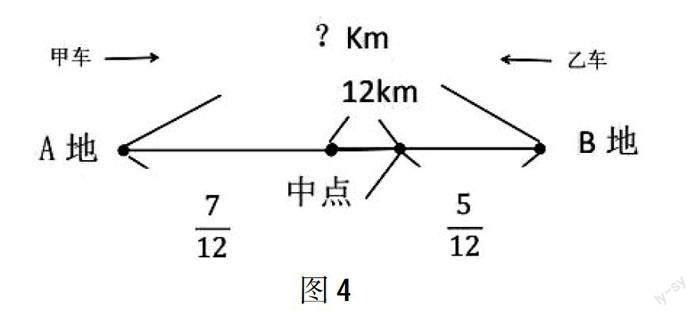
例如，教学“行程问题”：甲、乙两车同时从A、B两地相对开出，甲、乙两车速度比为7∶5，在距中点12千米处相遇。A、B两地相距多少千米？

学生根据文字信息，抓住关键句，理解题意：甲车速度比乙车快，它们相向而行，相遇时，甲车行的路程比全程的一半多12千米，而乙车行的路程比全程的一半少12千米。行驶时间相同，两车的速度比是7∶5，那么路程比也是7∶5，全程12份。接着画线段图（如图4），把抽象的数量关系转化为具体形象的图形表征，“看图说话”，帮助理解，问题也就迎刃而解了。

方法1：从线段图直观理解甲车行的路程是全程的７/12，超过中点12千米，12千米对应的是全程的（７/12-1/2），A、B两地相距：12÷（７/12-1/2）。

方法2：从线段图也可直观理解乙车行的路程是全程的5/12，还要再行12千米才能到达中点，12千米对应的是全程的（1/2-5/12），A、B两地相距：12÷（1/2-5/12）。

但有的学生错误地理解，认为甲车比乙车多行的路程是12千米，列出錯误的算式：12÷（7-5）×（7+5）。如何让学生形象理解“甲车比乙车多行的路程是2个12千米呢？”教师运用教学智慧，另辟蹊径，画出线段图（如图5），启发学生换角度思考问题：假设甲、乙两车是同向而行。教师借助线段图进行分析讲解，学生不难理解“甲车行的路程是7份，乙车行的是5份，甲车和乙车的路程差是2个12 千米，即24千米。”随即列出正确的算式：12×2÷（7-5）×（7+5）。还有的学生受到线段图的直观启发，发现一份路程是12千米，全程是12份，A、B两地相距：12×12=144（千米）。

综上所述，小学数学教学应立足几何直观，帮助学生理解抽象的数学知识。教师在平时教学中，注意结合教学内容和学生的认知水平，引导学生自觉运用几何直观开展数学活动和问题探究，将文字语言转化为图形、符号语言，化抽象为形象，化难为易，化繁为简，让思维过程可视化，实现各种数学语言的互译和对话，促进知识的理解和问题的解决，从而提高学生的数学思维能力，落实核心素养的培养。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.4

[2]程响.基于几何直观的问题解决教学[J].新教师，2017（11）：38-39