机器人气囊抛光位置误差建模及补偿
毛记祥,倪磊,向北平,舒龙飞
(西南科技大学 制造过程测试技术教育部重点实验室,四川绵阳 621010)
随着超精密光学元件的需求不断扩大,对光学加工技术的要求不断提高,光学系统中应用非球面可以极大的提高系统的成像质量,优化系统结构。非球面在航空航天,精密仪器中应用十分广泛,所以对于非球面的设计、加工受到了光学工作者的重视[1-3]。超精密技术的发展,非球面的加工质量和效率也获得了极大的发展。
作为超精密加工的重要手段之一,机器人气囊抛光技术的快速发展,极大的缩短了光学精密元件的加工周期,降低加工成本。在机器人气囊抛光方面,为提高加工精度,王朋和王飞等在抛光过程中运动精度控制,材料均匀去除方面进行了深入研究[4-5]。Walker 等[6]提出使用机器人进行快速抛光的技术,减少加工时间,缩短了抛光周期,并降低生产大型光学系统元件的风险。Márquez 等[7]基于CAD 数据的自动规划和编程系统,实现自动规划抛光路径和数控编程代码的生成,开发出一套抛光力恒定的模具抛光机器人系统。Kaltsoukalas 等[8]研制了一款五自由度抛光机器人,使用面形控制算法补偿加工速度,并重点研究抛光轨迹规划以及机器人运动轨迹的控制。黄智等[9]使用机械臂研究SiC 的抛光特性,经过七个周期的抛光,最终加工出RMS 为 62.3 nm 的非球面。针对抛光力不稳定的问题,Wu 等[10]通过音圈电机精确控制抛光力的大小,提高抛光效率,改善面形质量。
综上所述,机器人气囊抛光技术进行超精密加工已经取得了一定的进展,但是也存在着抛光面形精度差的问题,因此为了提高机器人气囊抛光的加工面形精度,本文分析了影响机器人气囊抛光面形精度的因素,提出一种误差补偿法来降低由机器人位置波动引入的误差,实验结果表明,经过误差补偿后,能够有效的降低气囊抛光系统中引入的误差,提高面形精度。
1 气囊抛光特性分析
气囊抛光是一种采用气囊结构,气囊外表面粘附聚氨酯抛光层,在一定浓度的抛光液的作用下,按进给运动,实现材料均匀去除的抛光方式。气囊抛光的材料去除特性是基于Preston 方程[11]构建的去除函数模型,即
式中:k为比例系数,受工件材料、气囊性质、抛光液浓度和环境温度等因素共同决定;p为抛光接触区域内的压力分布;v为接触区域内的抛光速度。
接触区域内的材料去除分布函数可以表示为
气囊抛光头与工件曲面接触时,抛光接触区域的速度将受到抛光头的变形以及工件表面曲率变化的影响变得复杂。气囊抛光的运动过程如图1 所示,气囊头与竖直方向存在夹角 α,气囊围绕自身轴线做角速度为 ω的回转运动,由于气囊具有一定弹性,在压力作用下气囊与工件的接触区域,气囊发生形变,使得气囊与工件紧紧吻合,气囊随着加工面型的曲率变化做出自适应变化,实现材料的均匀去除。

图1 气囊抛光的运动过程
对抛光接触区域内任意一点做运动分析,气囊与工件接触区域到气囊磨头轴线i的距离为 Δr,根据几何关系,则
式中e为抛光气囊压缩量。
接触区域内的线速度可以表示为
在抛光过程中,只有切向速度对材料有去除效果,抛光区域内的速度分布可分为切向速度和法向速度,根据速度合成公式,切向速度表示为
根据Hertz 接触理论,气囊抛光头与工件接触时,其接触区域为椭圆形,压力分布为
式中:m为压力系数;p0为平均接触压力,p0=(m+1)ke/(πab)。
通过以上分析得到气囊与工件接触区域内的压力和速度分布,将式(5)、式(6)代入式(2),则可以得到去除函数表达式由于Preston 常数k没有确定,无法得到准确的材料去除量,因此对去除函数模型进行归一化处理并仿真,仿真结果如图2 所示,去除函数图形大致呈高斯分布,面形平滑收敛且收敛性好。在接触中心区域内,材料的去除量最大,向边缘处逐渐减小,且过渡平滑,有利于材料的均匀性去除。由于气囊抛光进动角的存在,去除函数图形整体存在偏移。

图2 去除函数归一化仿真结果
2 误差分析及补偿
2.1 气囊抛光误差分析
在机器人气囊抛光中,抛光转速,工具倾角,抛光时间,抛光力大小等因素共同决定了最终加工面形精度。宋剑锋等[12]通过工艺参数的正交实验得出了不同因素对表面质量的影响程度,即气囊压缩量、抛光头转速、抛光液浓度、气囊内部压力的对面形精度的影响程度依次减弱。
对于整个机器人气囊抛光系统来说,提高加工面形精度主要从两方面入手,一是优化驻留时间算法,改善抛光工艺[13],二是降低系统误差和提高机器人定位精度[14-16]。在机器人气囊抛光中,抛光压力的稳定影响了面形精度,加工时保持气囊抛光压力的稳定,对于提高机器人气囊抛光加工面形精度具有重要意义。
气囊抛光压力的大小是由气囊形变和充气压力共同决定,即p=pε+pc, 在气囊的充气压力pc保持一定时,气囊的形变 ε决定了抛光压力,由于气囊材料采用橡胶气囊,在弹性限度内满足胡克定律F=Kε。
根据去除函数模型分析,抛光压力越大,材料的去除量越大。气囊加工中气囊压缩量超过0.5 mm时[17],去除特性曲线会发生畸变,不利于面形收敛。因此抛光时,气囊压缩量取0.3 mm,在橡胶气囊的弹性限度内,满足胡克定律。
抛光压力的波动影响去除函数的稳定性,不利于面形收敛。机器人末端位置误差影响了气囊的压缩量,从而引起抛光压力的波动,所以为降低抛光压力波动对去除函数的影响,要减少由机器人末端位置误差而引入的波动。
2.2 误差建模及补偿
机器人末端位置引入的误差分为X,Y,Z这3 个方向的位置误差和沿3 个方向上的线位移误差δX,δY,δZ,在进行气囊抛光时,工件处于XY平面内,因此只有Z方向的误差才会对抛光压力产生影响,且气囊形变在X,Y方向上引起Z方向的线位移误差 δX(Z), δY(Z)与Z方向上的位置误差相比可以忽略不计,因此该误差模型为只考虑机器人末端位置在Z方向上的位置误差所引起抛光压力变化。
本文以ER20-10C 型机器人作为气囊磨头载体,研究其在加工过程中的末端位置误差波动对加工工件面形的影响。根据以上分析,提出网格式误差补偿法,根据机器人气囊抛光特性,单位面积上的加工点位数较多,不能准确知道每一个加工点位的位置误差,因此将整个加工面进行网格划分,记录并保存网格节点pi,j处 的Z方向位置误差值并建立误差补偿节点数据库即
式中:h′为节点等分步长,规定节点位置处的位置误差量分别表示为则非节点pX,Y处的位置误差量δX,Y,通过三次样条曲线插值得出,即在任意的子区间内 , δX,Y存在函数关系,即
式中h为加工时栅格间距。
根据所得到的误差数据,生成误差数据模型,通过对该模型的即时调用,实现对加工点位的位置进行修正。加工点位pX,Y处的位置量为zX,Y,修正后该点位的位置量为即满足
根据误差补偿模型,设置该模型的实验参数值,h′= 5 mm,n=m= 11,以该参数为基础节点,记录机器人末端位置误差值,根据所测量误差数据,计算出所有加工点位误差值,并绘制加工点位的误差波动图,如图3 所示,机器人在工件平面进行抛光时,末端位置存在一定程度的波动,影响抛光压力的稳定。

图3 机器人末端位置误差波动图
根据上述补偿方法及误差数据对该机器人进行位置误差补偿实验,为了保证补偿效果,设置补偿前后的测试点与误差数据库的节点位置相异,将补偿前后机器人末端位置误差进行对比验证,如图4 和图5 所示,由实验结果可知,未进行误差补偿时,工件范围内机器人末端位置误差X方向的PV 值为0.152 mm,经过误差数据补偿,机器人末端位置PV 值降为0.021 mm,Y方向的末端位置误差PV 值由补偿前的0.037 mm降低至补偿后的0.012 mm。X和Y方向的误差波动范围相比于补偿前分别降低了86.2%和67.6%。

图4 X 方向补偿前后误差对比

图5 Y 方向补偿前后误差对比
实验数据表明,机器人补偿后末端位置误差大幅下降,极大的提高了机器人位置精度,降低抛光压力的波动,有利于面形加工。
3 实验验证
为了验证误差补偿法的可行性,通过机器人末端法兰连接气囊磨头进行光学镜面加工。根据上述误差模型及补偿方案,进行机器人气囊抛光特性实验。为验证补偿效果,采用两块材质相同的K9 玻璃进行实验对比,口径均为100 mm。抛光轨迹采用光栅型轨迹抛光,各工艺参数保持一致,忽略其他因素的影响,对照组实验正常加工,实验组进行误差补偿。加工过程如图6 所示,实验工艺参数如表1所示。对照组镜面的初始面形精度PV 为1.573λ,RMS为0.456λ,经过一个周期的抛光,面形精度收敛到PV 为1.43λ,RMS 为0.158λ,如图7 所示,加工收敛率达65.4%。未进行误差补偿的加工面形与机器人位置误差波动趋势相似,证明了机器人的位置误差确实对加工面形产生一定的影响。

表1 气囊抛光实验参数表

图6 气囊抛光实验过程

图7 未误差补偿加工面形图
根据误差模型数据,将误差数据补偿到加工程序中,在实验组镜面上进行抛光验证,抛光前的面形精度PV 为1.661λ,RMS 为0.475λ。经过一个周期的补偿加工,重新加工后整体面形精度达到PV 为1.053λ,RMS 为0.118λ,误差补偿后的面形收敛率为75.2%。补偿结果如图8 所示,面形精度补偿前后的RMS 分别为0.158λ和0.118λ,面形收敛率提高了25.3%。证明该方法在一定程度上降低了机器人末端位置波动的影响,提高了面形精度。
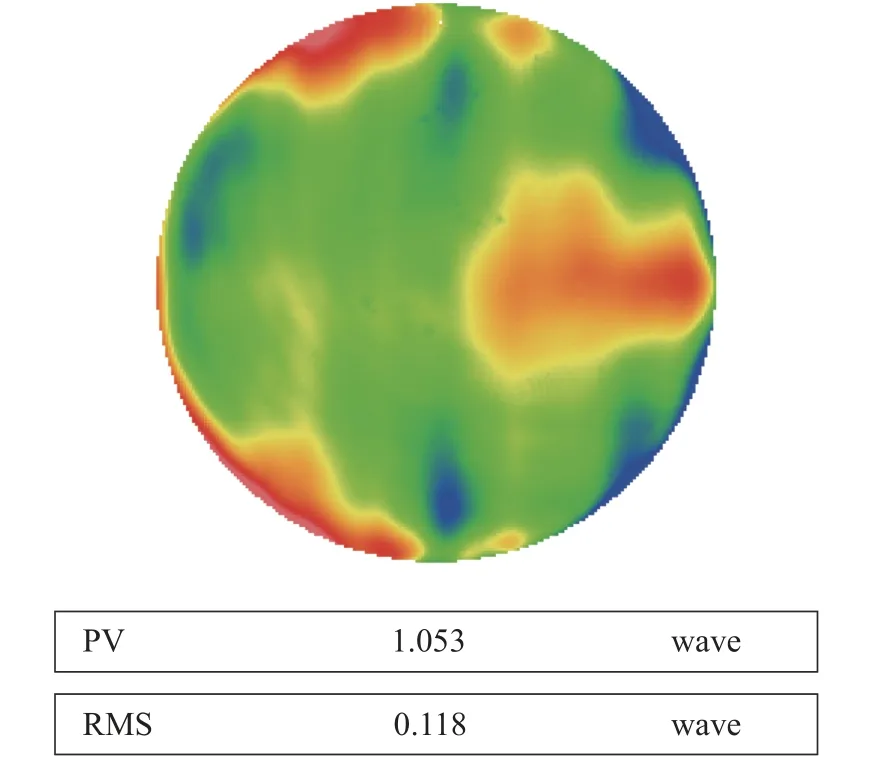
图8 补偿后面形抛光结果
4 结论
1)根据机器人气囊抛光的进动运动形式,构建去除函数理论模型,计算仿真去除函数图形,仿真结果表明去除函数图形呈高斯分布,有利于气囊加工的面形收敛。
2)针对由机器人末端位置误差引起的抛光压力不稳定问题,建立误差补偿模型,误差补偿后机器人末端位置X,Y方向的误差波动,仅为原来的13.8%和32.4%,证明了该方法能够有效的提高机器人末端位置精度。
3 )通过机器人进行气囊抛光误差补偿实验,实验结果表明该方法能够降低由机器人位置误差引起的压力波动对面形精度的影响,最终加工面形精度RMS 为0.118λ。改善了机器人气囊抛光的加工面形精度,提高了面形收敛效率。

