托辊非接触式故障识别方法研究
郝洪涛,苏耀瑞,丁文捷,冯宝忠
(1. 宁夏大学 机械工程学院,银川 750021;2. 宁夏天地西北煤机有限公司,宁夏石嘴山 753000)
远程带式输送机凭借它运输距离远、结构简单、输送能力强等优点被广泛应用到散料运输中。托辊作为带式输送机重要的部件,数量众多,一旦发生故障极易引起大的事故。传统托辊检查一般是通过工人巡检,效率和识别率都很低。近年来,智能巡检机器人被引入到安全巡检中,Tang 等提出了采用智能巡检机器人检测钢轨的方法,取代了人工检查工作,很大程度提高了检查效率[1]。针对变电站室内巡检问题,Zhao 等采用智能巡检机器人解决,在变电站水冷室得到了验证[2]。虽然现有的基于加速度信号轴承故障诊断技术较成熟[3],但是托辊数量众多,此类方法需要大量的传感器,而且现场环境恶劣,接触式信号采集方法容易受干扰,适用性差。声音信号凭借其非接触特点,近年在机械故障诊断中较为凸显,能克服加速度信号等接触式故障诊断方法带来的不足。综上所述,本文采用智能巡检机器人搭载拾音器的方式,进行托辊巡检。
托辊所处环境恶劣,如何从复杂的噪声环境中提取出托辊内部轴承声音信号尤为重要。盲源分离能够在未知混合过程及源信号的条件下,从观测到的混合信号中恢复出源信号的波形,适用于剔除干扰[4]。巡检机器人搭载单个拾音器属于单通道盲源分离问题。目前解决单通道盲源分离方法通常为“两步法”,即先根据观测信号估计得到混合矩阵,再通过优化算法实现源信号的分离[5]。李静娇采用小波包分解估计混合矩阵,用FastICA 实现源信号的分离,应用在滚动轴承信号提取中[6]。Xu 等用集合经验模态分解(Ensemble empirical mode decomposition,EEMD)和PCA 估计混合矩阵,用RobustICA 实现分离,在轴承故障分离中得到验证[7]。EEMD 方法虽然解决了经验模态分解(Empirical mode decomposition,EMD)的模态混叠,但是存在噪声残留;小波包分解需要提前对小波基函数和分解层数选取且缺少理论指导,自适应性不高[5]。FastICA 需要预处理,可能引器误差[8]。声音信号特征参数提取中,MFCC 被广泛应用到各个领域。Cao 等针对土方设备识别问题,引入MFCC 特征提取方法并验证了其有效性[9]。王前等采用MFCC 和PCA 结合的方式,成功实现轴承声音信号特征参数提取,并有较高的识别率[10]。但是MFCC 由于利用分帧满足梅尔倒谱系数提取中傅里叶变换的条件,导致它对非线性和非平稳性的信号刻画能力不够[11]。
针对以上分析,提出基于CEEMDAN-PCA-Robust -ICA 的单通道盲源分离方法。采用CEEMDAN 可很好解决EMD 的模态混叠和EEMD 的噪声残留问题,RobustICA 能够克服FastICA 需要预处理问题,而且RobustICA 采用峭度的完整表达式作为目标函数,具有较快的收敛速度和较好的鲁棒性[12-13]。提出基于CEEMDAN、PCA 和MFCC 的特征参数提取方法。利用CEEMDAN 和MFCC 结合,将信号分解成具有平稳特性的IMF 分量后,用PCA 剔除特征贡献率小的分量,再进行傅里叶变换,而且对比单独实用MFCC,能够基于信号的特性自适应分解信号[14]。最后提取MFCC 的一阶差分系数和Delta,展示出信号的动态特征。采用具有唯一全局最优解的支持向量机作为分类器[15]。利用实验室智能巡检机器人和故障模拟实验台模拟托辊现场数据采集,利用采集到的数据进行测试,结果表明提出的托辊信号的提取及识别方法是有效的。
1 CEEMDAN-PCA-RobustICA 单通道盲源分离
1.1 CEEMDAN 算法介绍
互补经验模态分解(Complementary ensemble empirical decomposition, CEEMD)能够减少EMD的模态混叠现象,消除集合经验模态分解EEMD 噪声残留问题,但是依旧存在信号分解不完备和运算量大等问题。基于完全噪声辅助集合经验模态分解(Complete ensemble empirical mode decomposition with adaptive noise, CEEMDAN)通过在信号分解的每个阶段去添加自适应的高斯白噪声,然后计算残余向量得到各个模态分量,很好的解决了此问题[16-17]。具体计算步骤如下:
1)添加m(i=1,2···,m)次满足正态分布的高斯白噪声ni(t)到 原始信号xi(t)中 ,即si=x(t)+ni(t),对信号si(t) 进 行EMD 分解,获取第一个分量。
残余分量r1(t)=x(t)-IMF1。
2)添加m(i=1,2,···,m)次满足正态分布的高斯白噪声ni(t)到 残余分量r1(t) 中 ,即对信号进行EMD 分解,获取第一个分量。
3)重复上述步骤,每次分解都会得到一个IMFn分量,当满足EMD 分解的终止条件时,迭代停止。假设重复了k次,则,最终信号x(t)被分解为
1.2 PCA 算法
主成分分析算法(Principal component analysis,PCA)是常用的线性降维方法,在故障诊断应用较为广泛。PCA 算法是通过某种线性投影,在一定的信息损失范围内,将n维数据的多个特征属性映射为能够代表源数据特征值的k维数据(n>k)。很好的缓解了维度灾难问题,提高了机器学习的效率[18-19]。
主成分分析方法的主要步骤如下:
1)对原始数据进行标准化处理
假设原始数据有m个样本,每个样本有n个特征,其可以表示为一个m×n的矩阵X,即
计算n个特征的平均值,即
然后,对所有的样本,每一个特征都减去对应的均值。
2)计算协方差矩阵C
3)计算协方差矩阵C的特征值和特征向量
首先寻找一个矩阵P,满足PCPT是一个对角阵,再找n个单位正交特征向量组成矩阵E=(e1,e2,···,en),完成对角化,即
每个特征值 λi都有对应的特征向量 εi。
4)降维的计算
若将m×n的 矩阵降维至k×n,降维矩阵取E的前k行,即Ek。
1.3 RobustICA 算法介绍
RobustICA 是ICA 算法一种,但是对比传统ICA 算法,它无需白化预处理,减少了工作量;采用最佳优化步长技术,提高了目标函数的鲁棒性;具有较高的收敛速度。同ICA 算法一样,RobustICA 也包括两部分内容:目标函数和优化算法[20]。
1)目标函数
选取不同的目标函数就是从不同角度提出对分离结果各成分独立性的评价,即在求解源信号时,当W作用于观测信号x 后,需要选择合适的目标函数去度量最终结果的非高斯性。Robust ICA 以峭度为目标函数,具有很强鲁棒性。在统计学中,峭度是表征随机变量非高斯性最简单的指标,虽然峭度对渐进方差和野点相对敏感,但是它在整个处理过程中的计算简易和易于收敛等特点使得它在ICA 中普遍应用[21]。
假设观测数据为x,设输出信号y=ωix,则其峭度定义为
2)优化算法
确定好目标函数后,Robust ICA 将精确线性搜索最优步长作为优化算法,使目标函数最大化。以峭度作为目标函数,精确线性搜索方法表达式为
式中g为精确线性搜索方向,一般为梯度。
在实际应用中,精确线性搜索计算复杂。由于峭度可以表示成 µ的多项式或有理函数,所以全局最优步长 µopt可以借助寻找多项式的根来确定。在每一次迭代运算过程中,Robust ICA 获取最优步长的步骤如下:
1)计算最优步长多项式系数,以峭度为目标函数,其最优步长多项式为
2)求解最优步长多项式p(µ)的 根
3)选择沿搜索方向峭度绝对值最大值为多项式p(µ)的根,即
4)根据最优步长 µopt更新分离向量,即
5)对分离向量进行归一化,即
1.4 CEEMDAN-PCA-RobustICA 算法介绍
解决单通道盲源分离问题通常采用“两步法”:第一步根据观测信号估计出混合矩阵;第二步通过优化算法实现分离[5]。混合矩阵估计采用基于观测信号扩维方法中自适应强且通过EMD、EEMD和CEEMD 优化而来的CEEMDAN 算法。CEEMDAN将观测信号分解为多个IMF 分量,然后采用主成分分析算法对IMF 分量进行筛选降维,确定源信号个数,将剩余IMF 分量重构信号,采用RobustICA 算法实现源信号的分离。最终将分离出的信号计算与源信号的相关性,取相关性值最大的信号作为最终分离的结果。CEEMDAN-PCA-RobustICA 算法如图1 所示。

图1 CEEMDAN-PCA-RobustICA 算法示意图
2 CEEMDAN-PCA-MFCC 特征提取
2.1 MFCC
Mel 频率倒谱系数(Mel frequency coefficient,MFCC)是根据人耳对不同频率的声音具有不同的感知能力提出的,是声音识别相关研究中常用的声音特性分析方法。MFCC 特征提取包括预处理,离散傅里叶变换,计算谱线能量,Mel 带通滤波,离散余弦变换等步骤[22-23]。图2 为MFCC 特征参数提取原理框图。
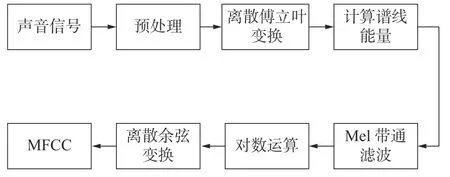
图2 MFCC 算法示意图
不同频率f与Mel 频率之间的关系式为
算法具体流程如下:
1)预处理主要包括预加重、分帧、加窗。其中,预加重的目的是补偿高频分量的损失。预加重是通过添加数字滤波器实现的,滤波器常设置为
分帧是为了将一个非稳态信号,通过将它分成较短的帧,就可以将它看成稳态信号,一般每帧的宽度为20 ~ 40 ms。为了将每帧之间能更好的过渡,在相邻两帧之间增加帧移。加窗的目的减小频域中的泄露,具体是将每一帧都要乘以窗函数 ω (n),此处选用的是hamming 窗,具体表达式为
2)对预处理后的每帧信号进行离散傅里叶变换(DFT),设预处理后的信号为x(n), 变换后为X(k)。
式中N为傅里叶变换的点数。
3)先将X(k)平方后,再通过Mel 频率滤波器组得到Mel 频谱,再取对数得到对数频谱S(m),即
式中:M为滤波器的个数;Hm(k)是每个滤波器的传递函数。
4)最后,将S(m)进行离散余弦变换(DCT),就可以得到MFCC,过程为
2.2 MFCC 的差分系数
MFCC 能很好的提取声音信号的特征参数,但是仅限于静态特征的提取。如果想要提取声音信号的动态特征,就需要经行MFCC 的1 阶2 阶差分系数的计算。在成功提取MFCC 后,即可进行MFCC的1 阶2 阶差分计算[24]。
MFCC 的1 阶差分系数记为 Δ MFCC,其计算公式为
式中c(n)为一帧声音信号的MFCC 特征参数序列MFCC 的2 阶差分系数记为Delta。
式中:Dt为第t帧MFCC 特征的Delta 特征; Θ为第t帧时序变化的信号帧的数量。
2.3 CEEMDAN-PCA-MFCC 算法
托辊内部轴承声音信号是一种非线性、非平稳的信号,如果只提取声音信号的MFCC,会忽略声音信号的动态特征,所以提取声音信号的MFCC 后,还需要计算MFCC 的1 阶差分系数和2 阶差分系数。但是,对于非线性、非平稳性的刻画,仅加差分系数是不够的,需要将能精细刻画信号非平稳性的CEEMDAN 和MFCC 结合,才能将轴承声音特征参数更完整的提取出来。为了进一步降低运行时长,引入主成分分析进行降维,最终采用支持向量机进行识别。CEEMDAN-PCA-MFCC 算法如图3 所示。

图3 CEEMDAN-PCA-MFCC 算法示意图
3 实验验证
3.1 实验设计
为了验证算法的有效性,设计了模拟实验验证方案:由美国SpectraQuest 公司生产的机械故障模拟实验台(MFS)模拟托辊运行故障,并利用自行研制的智能巡检机器人搭载拾音器进行巡检。其中,轨道有效长度为4 m,轨道与机械故障模拟试验台的距离为0.4 m,如图4 所示。托辊内部轴承的好坏决定着托辊是否正常运行,所以采用故障轴承模拟故障托辊,为更好还原托辊工况,添加5 kg 负载。在MFS 模拟实验台上,分别模拟运行轴承的正常、滚动体故障、内圈故障和外圈故障4 种状态。实验台电机转速设为1 800 r/min,智能巡检机器人巡检速度设为0.5 m/s,拾音器采样频率设为22 050 Hz。4 种状态轴承的声音信号前5 000 个采样点波形如图5 所示。

图4 托辊信号模拟采集示意图

图5 信号时域波形
其中,外圈故障有明显周期性波形出现,其他3 类信号时域无明显特征,且信号幅值较外圈故障小。
3.2 欠定盲源分离
将4 种状态轴承声音信号分别进行CEEMDAN运算,PCA 特征贡献率设置为95%,计算剩余IMF 分量个数。剩余IMF 分量所占比重如图6 所示。
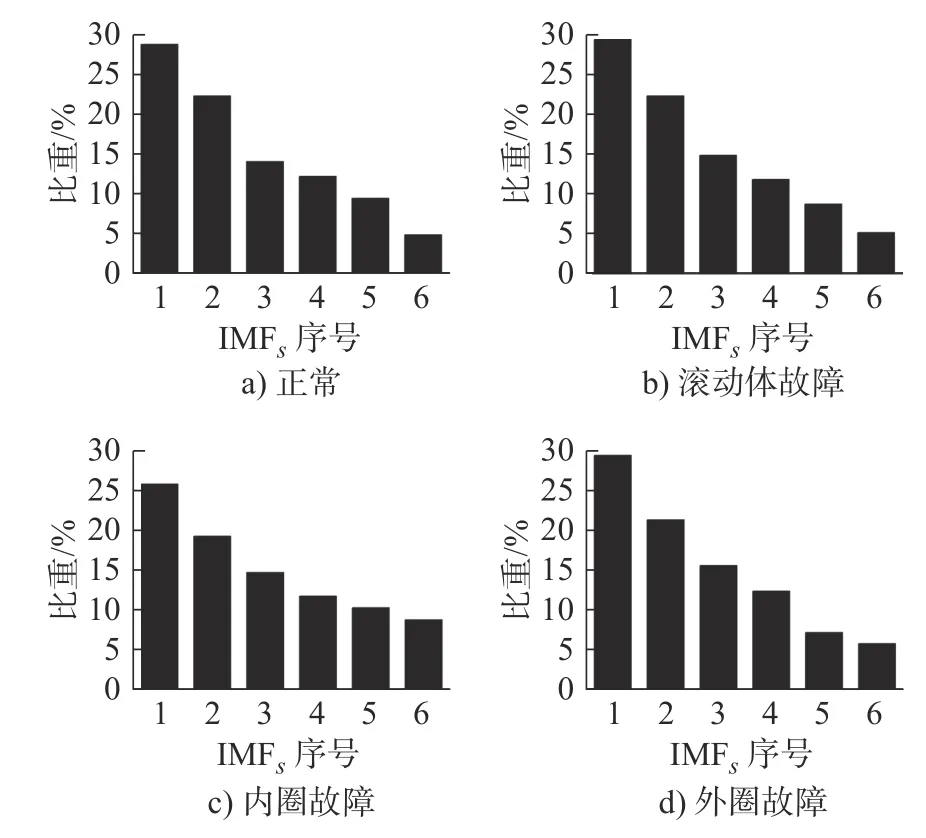
图6 剩余IMF 分量所占比重
将轴承的4 种状态下确定出的IMF 分量进行信号重构,进行RobusICA 计算,得出分离信号,再计算各个分离信号与源信号的相关性,各分离信号与源信号相关性值如表1 所示。以相关性值最大的分离信号作为最终剔除干扰后的轴承声音信号。由表1 可知,正常状态的第4 个分离信号、滚动体故障状态的第6 个分离信号、内圈故障状态的第5 个分离信号和外圈故障的第6 个分离信号分别为4 种状态最终的分离信号,图7为分离信号时域波形。

表1 各分离信号与源信号相关性值
由图7 可知,经过单通道盲源分离处理后,将高频噪声明显剔除,内圈和滚动体故障信号比其他两类信号弱,外圈故障信号较强。
3.3 特征提取
为了验证提出方法的有效性,需进行不同特征提取方法识别结果的对比,提取方案如表2 所示。

表2 特征提取方案
具体参数设定如下,PCA 特征贡献率设定为95%,剩余的IMF 分量进行MFCC 提取并且计算其1 阶和2 阶差分系数。提取MFCC 特征时,每1 024个点分为一帧,帧移设为300。MFCC 滤波器个数设为12,对每一帧信号提取MFCC,特征维度为12,再计算MFCC 的1 阶差分系数和2 阶差分系数,特征维度扩大到36。每一类信号各自提取1 500 个样本,总计6 000 个样本。图8 为正常轴承前500 样本的前四维特征值展示。
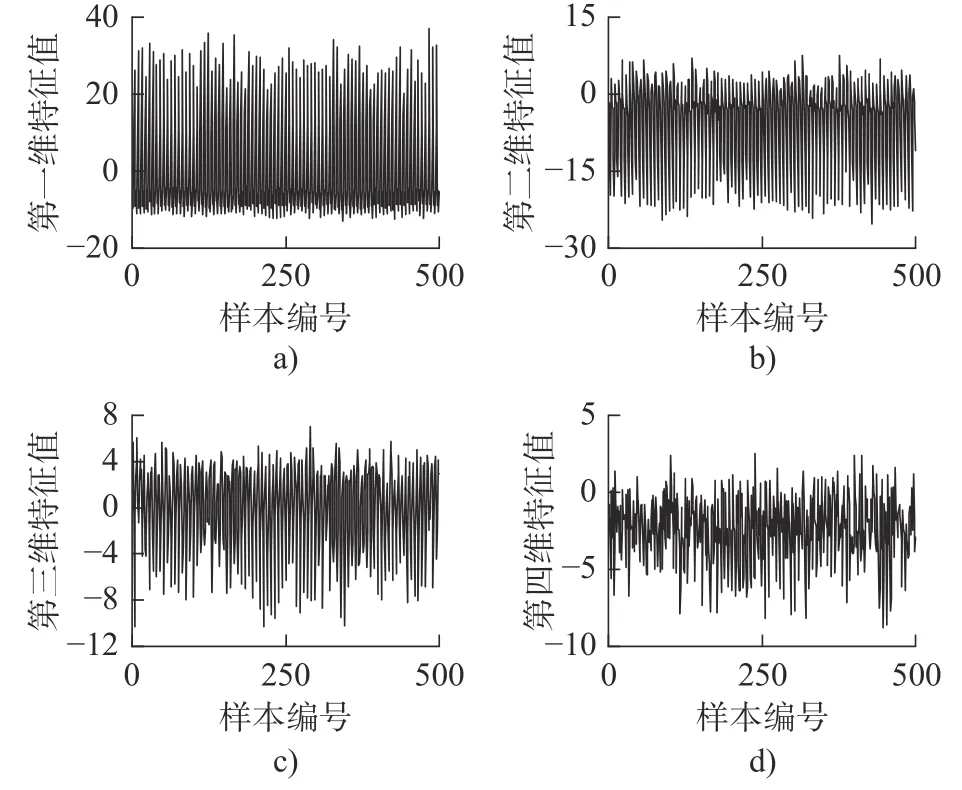
图8 正常轴承前四维特征值
3.4 识别结果及分析
为了验证识别算法的有效性,将6 000 个样本按训练样本与测试样本2∶1 的比例进行实验,即每类信号随机取1 000 个样本,总计4 000 样本用于训练SVM 模型;取每类信号剩余的500 个样本,总计2 000样本用于测试。程序运行平台为Windows10 系统、CPU Inteli5-10210U1.6Hz、采用基于LIBSVM 工具包的支持向量机识别模型作为分类器,核函数采用径向基核函数,参数优化方法选为网格优化,PCA进行最终特征筛选。用不同的特征提取方法进行识别,结果对比如表3 所示。

表3 不同特征提取方法的识别结果
对表3 分析可知,特征参数MFCC 四类准确率最高为97.8%,最低为45.4%,从不均匀的识别率中可以看出,MFCC 不能对较弱信号的特征实现完整提取,需要添加能精细刻画信号特征的EMD 和MFCC 差分系数。E + MFCC + 差分的结果验证了EMD 和差分系数的有效性,结果显示其能够均匀且较好的识别四类信号,但是由于自生的模态混叠问题,使整体的准确率没有较大的提高,需要采用CEEMDAN 改进。C + MFCC + 差分在E + MFCC + 差分的识别率上又有了进一步的提高,验证了CEEMDAN能够有效改进整体方法因为EMD 的模态混叠导致准确率低的问题。但是除了外圈故障,其他3 类故障准确率并未得到有效提高,可能为故障信号微弱,其他噪声干扰导致。由B + C + MFCC + 差分识别率可知,加入BSS 后可以很好提取出故障信号,消除了噪声干扰的影响。
但是整体训练时间较长,难以保证实时性,所以智能巡检机器人的巡检方案设定为,在巡检过程中,将采集数据储存到智能巡检小车的下位机中,巡检结束后将数据传输到上位机中进行数据分析,一旦发现异常数据,通过设定RFID 标签,追溯到故障托辊位置,通知工作人员检查。
为进一步验证整体算法的抗噪性,分别将信噪比为0 ~ 4 dB 的白噪声加入采集到的轴承声音信号中进行识别验证,结果如图9 所示。
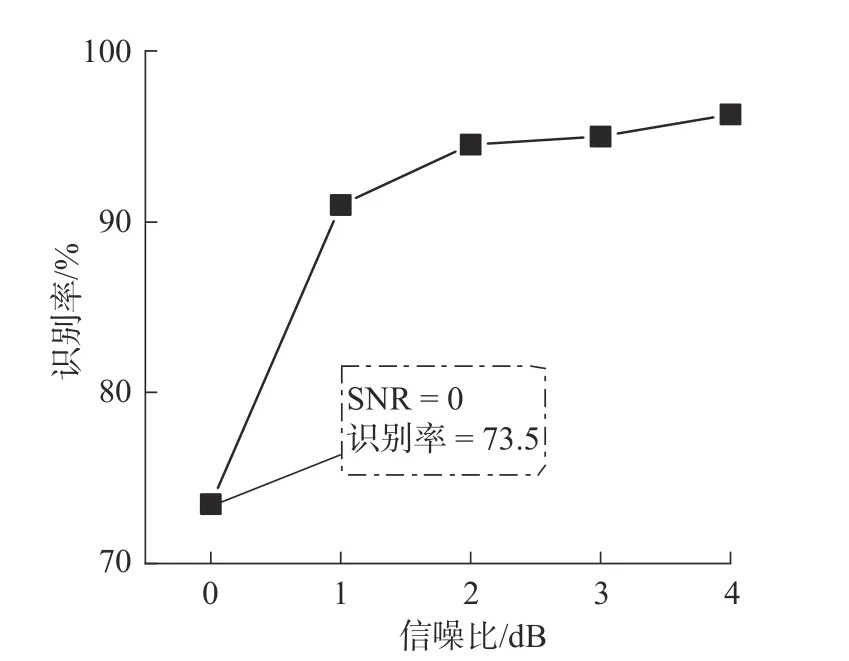
图9 不同噪声环境下的识别结果
由图9 可知,信噪比为0 时,整体算法识别率仍保持在73.5%;随着信噪比的升高,当信噪比大于1 dB时,算法准确率能保持在90%以上。间接证明了整体算法能在噪杂的矿山环境中,有效识别托辊故障。
4 结论
1)采用智能巡检机器人搭载拾音器非接触式采集托辊信号可以解决现有接触式加速度信号采集带来的信号收集困难及传感器需要数量多的问题。
2)用CEEMDAN 将信号自适应分解成平稳IMF分量,再进行MFCC 提取,能够实现非平稳信号特征参数的有效提取,在托辊信号特征提取方面识别率能达到90%。
3)托辊所处环境恶劣,针对条件有限的单拾音器采集问题,可用基于CEEMDAN-PCA-RobustICA单通道盲源分离方法,能有效剔除干扰噪声,将整体识别率提高7%左右。结合提出的特征提取方法,具有97.2%的识别率。最终提出可行的巡检方案,让远程带式运输机托辊采用智能巡检机器人搭载拾音器巡检方式变得可行。

