模糊贝叶斯网络在启动系统可靠性中的应用
钱存华,张洋洋
(南京工业大学 经济与管理学院,南京 211816)
发动机启动系统的运行稳健是保障飞机安全运行的关键。航空涡扇发动机启动系统的结构复杂、维护技术难度高且成本较大,若能及时对启动系统可能发生的故障问题进行提前预防或事后进行快速准确的故障判断,将有效降低故障概率并节省维修时间及费用,提高飞机的安全性和可靠性。因此,对飞机发动机启动系统的可靠性研究具有十分重要的现实意义。
在贝叶斯网络的方法研究中,Hamza 等[1]论述了贝叶斯网络在可靠性和安全性分析中对于故障树的优势;Tchangani 等[2]通过动态贝叶斯方法考虑复杂系统网络内对不可传播机制的建模;朱林等[3]探究了贝叶斯理论在结构件健康状态评估中的应用;贝叶斯模型广泛应用于系统的可靠性分析中[4-7],但由于许多系统实际运行机理复杂,贝叶斯网络往往难以构造,利用故障树的转化解决了这一主要问题[8]。张梅等[9]利用故障树和贝叶斯网络为矿井提升机的故障诊断提供方法;许保光等[10]通过故障树和贝叶斯网络模型对影响航空安全的关键因素进行重要程度研究。然而,在实际工程中许多系统的故障数据可能并不充分,事件间的联系也并非精确已知,所以传统故障树的适用性不强。因此,引入模糊技术是解决贝叶斯网络模型及其适用问题的重要途径[11-12]。
将贝叶斯网络与T-S 模糊故障树法相结合,通过构造T-S 门并用梯形模糊数描述系统组件的故障概率,加入重要度分析后可提供一种计算飞机涡扇发动机启动系统故障概率的模型方法。通过实例分析启动系统中各基本事件的故障概率,找出系统中易发故障的薄弱环节,帮助提升航空涡扇发动机启动系统预防与维修的工作效率。
1 模糊可靠性评估方法
1.1 模型基本理论
贝叶斯网络(Bayesian network,BN)的基本模型如图1 所示,由连接系统的根节点x、中间节点y和叶节点T的有向边组成,特征为有向无循环,节点之间的关系强度由条件概率表达。
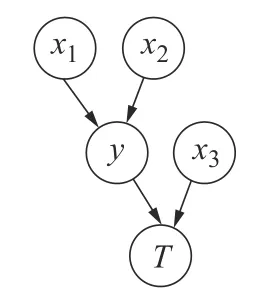
图1 BN 模型
贝叶斯模型具备描述事件及多态事件的逻辑关系简便和计算分析能力强大的优点,利用贝叶斯理论[13]计算模糊模型后验概率的方法为
1.1.1 T-S 模糊故障树
故障树模型(Fault tree, FT)由不同层级事件依据逻辑关系组成。模型先确定顶事件,再确定能够引起顶事件的充分必要的直接原因(即中间事件),中间事件按照因果关系逐级向下发展直至最后一行的底事件,最后需要根据被评估系统的运行机制确定逻辑门关系,将各级事件联结起来。传统的故障树模型在描述系统或零部件的多态性和故障数据的不确定性上具有一定的局限,而T-S模糊故障树的出现[14]恰好可以弥补这一不足。将原始故障概率通过梯形模糊处理,并构造T-S 门确定事件间的联系。T-S 模糊故障树的简单模型如图2 所示,其中,xi和y则分别表示模型构成的底事件和中间事件,T为顶事件。

图2 T-S 模糊故障树模型
1.1.2 由T-S 模糊故障树构造贝叶斯网络
故障树模型中的底事件对应贝叶斯网络根节点,底事件的概率在贝叶斯网络中由根节点的先验概率表示,中间事件和顶事件对应网络中间节点和叶节点,连接事件的逻辑门在BN 模型中则由条件概率表示。
将T-S 模糊故障树法与贝叶斯网络相结合,采用经过专家经验和梯形模糊处理后的故障数据作为贝叶斯网络中根节点的先验概率,使T-S 模型解决事件间联系的不确定性问题,同时利用贝叶斯网络填补故障树法不能反向推理的空缺。
1.2 模型算法与重要度分析
为减少历史故障数据的不确定性为系统可靠性分析带来的影响,应首先将发动机启动系统的原始故障数据利用梯形模糊数进行区间表征。将故障程度分为无故障、轻度故障和完全故障,由在区间[0, 1]上的模糊数表示,并分别使用0、0.5 和1 描述。
式中: s为模糊集的左右支撑半径;f 为左右模糊区;M0为 梯形模糊数支撑集的中心; µ (F)表示梯形函数中模糊集的隶属度。当s = f = 0 时,模糊程度退化为原始数据且只能用于传统的二态描述,因此采用模糊数计算更具有评估系统多重故障状态的能力。
如图3 所示为梯形模糊隶属函数在坐标系中的表示。
1.2.1 T-S 模型算法
作为一种模糊推理模型,T-S 模糊故障树是由IF-THEN 的模糊规则和T-S 门组成的较复杂的非线性函数,可以描述多重事件间复杂的相互关系。现假设基本事件x = ( x1,x2,···,xn) 和上级事件b的故障程度分别为和那么有:
已知规则 l(l=1,2,···,n), 若 x1的 故障程度为且可由T-S 门运算规则得到 b的故障程度为 b1的 可能性为 pl(b1), 为 b2的可能性为pl(b2),···,为 bkn的可能性为pl(bkn),in=1,2,···,kn,且有:
若假设故障树模型中各基本事件已经处于不同程度的故障状态,且其故障的模糊可能性为则 规 则l(l=1,2,···,n)的模糊可能性为
上级事件发生故障的模糊概率为:
此时将式(6)结合T-S 门运算规则便可由下而上的推断模型中各事件的模糊概率。
1.2.2 模糊重要度
根据姚成玉等[15-16]对重要度分析方法的研究,假设贝叶斯网络中某根节点 xj处于的故障状态,其失效可能性的模糊子集为隶属函 数 为则叶节点 T 的故障状态为 Tq的失效可能性的模糊子集为隶属函数为此时,当 xj处于的故障状态时对叶节点T 为Tq的模糊重要度为
式中:和为根节点 xj为的失效可能性的模糊子集为0 或1 时使得叶节点T 为Tq的失效可能性模糊子集。两积分项将叶节点的模糊子集精确为具体值。那么, xj对叶节点产生影响的T 为 Tq的模糊重要度计算方法为
1.2.3 状态重要度
当系统中某一组件 xj发生故障,假设其故障状态为那么此时组件所处故障状态对系统贝叶斯
网络中叶节点T为Tq的状态重要度为
1.3 启动系统的故障诊断原理
在调研了大量相关文献与资料的基础上,确定了某型航空涡扇发动机的基本结构组成。其发动机系统主要由8 个功能不同的子系统构成,根据各子系统的主要功能与作用,决定以涡扇发动机系统的启动系统为例,研究启动系统的健康状态为发动机整体带来的影响。
已知航空涡扇发动机启动系统的主要故障类型对应贝叶斯网络中各基本事件的根节点,通过收集分析启动系统的历史故障类型数据,将发动机启动系统故障的基本事件与中间事件分别用xn和yn表明,列出具体故障类型及相应节点如表1 所示。
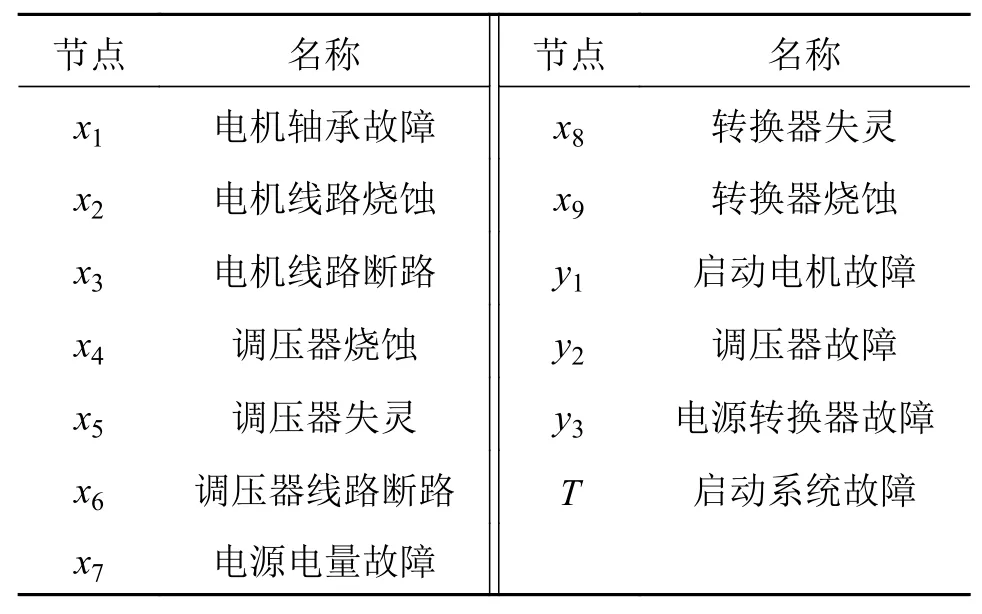
表1 BN 各节点及名称
此时经过分析涡扇发动机启动系统的结构与功能,可确定评估系统可靠性的基本步骤如图4 所示。
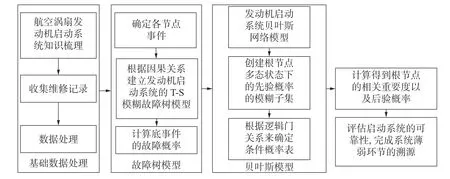
图4 启动系统故障诊断原理
1.4 发动机启动系统的T-S 模糊故障树
由启动系统各节点事件的因果关系,结合专家经验的同时加入T-S 门规则,可得到航空涡扇发动机启动系统的T-S 模糊故障树模型,如图5 所示。

图5 启动系统的T-S 模糊故障树
2 航空涡扇发动机启动系统可靠性实例分析
2.1 启动系统的模糊贝叶斯网络
航空涡扇发动机启动系统的主要结构由启动机、启动点火装置和电气控制开关组成,一般由飞机内部电源或外部电瓶电源的方式供电,由操作室的电动开关控制。其中,启动点火装置还包括磁电机和火花塞等。
涡扇发动机启动系统的运行主要靠电能的转化,推动发动机转子的高速旋转,使飞机的启动系统可以在地面时或者滑行过程中充分预热。启动系统可靠性的高低会直接关系到机组相关人员的飞行安全,同时对涡扇发动机的健康状态和飞机的运行过程产生尤为重要的影响。
由故障树与贝叶斯网络的映射关系,使用T-S模糊故障树构造涡扇发动机启动系统的贝叶斯网络模型如图6 所示。

图6 启动系统的贝叶斯网络
2.2 数据处理与计算分析
由启动系统的T-S 模糊故障树,联系各故障事件节点计算启动系统各组件故障的模糊可能性,并由故障状态推理出各组件故障程度的模糊可能性。现假设贝叶斯网络中所有节点可能处于无故障、轻度故障和完全故障3 种状态,采用梯形隶属函数计算,相关参数选取sr=sl=0.1、fl=fr=0.2。
计算得到根节点x1~x9的故障率及故障状态为1 的模糊子集如表2 所示。此时,在加入专家经验的基础上结合模糊处理后的历史故障数据,得到条件概率如表3 所示。

表2 根节点故障概率及模糊子集

表3 中间节点y 1的条件概率表
2.2.1 叶节点的故障概率模糊子集
将根节点的概率模糊子集结合中间节点y1~y3和叶节点T的条件概率,可由式(4)~式(6)得到T分别为0、0.5 和1 这3 种故障状态时的故障概率模糊子集为:2.2.2 叶节点模糊概率
假设每个根节点的故障状态用模糊数表示为:x1=0.2,x2=0.4,x3=0.1,x4=0.5,x5=0.2,x6=0.1,x7=x8=x9=0,那么可利用公式得到叶节点T处于不同故障状态的模糊概率分别为:
2.2.3 状态重要度与模糊重要度
由重要度计算方法得到各根节点对叶节点T故障状态为0.5 和1 的状态重要度和模糊重要度,如表4 和表5 所示。
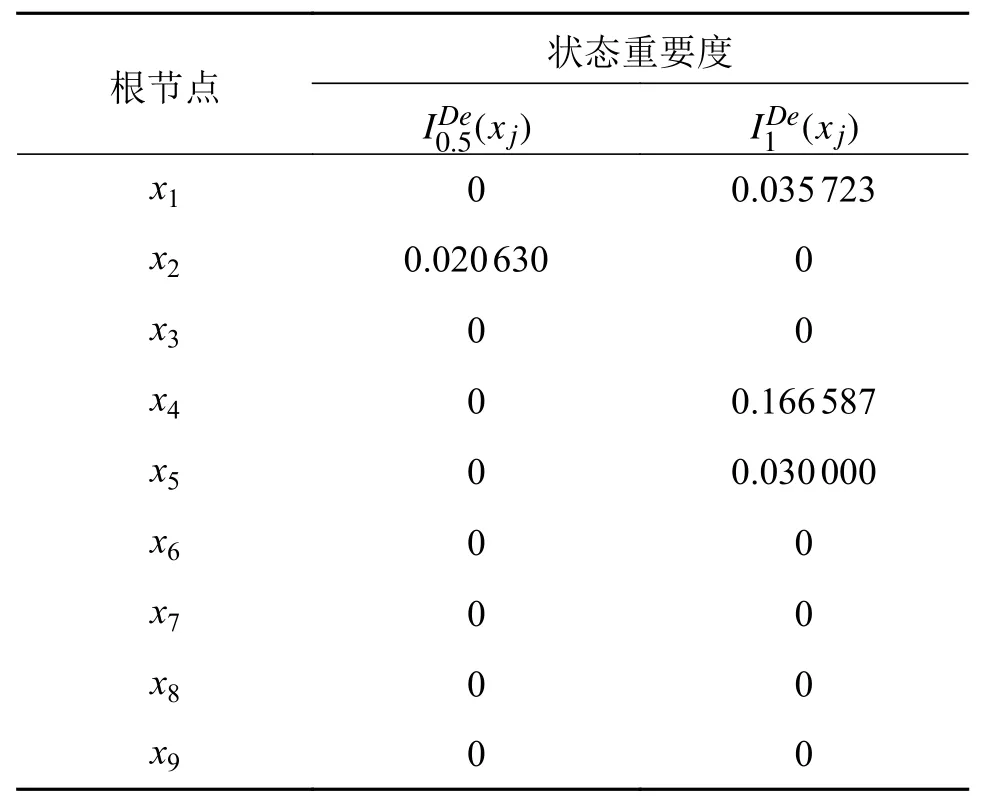
表4 根节点状态重要度

表5 根节点模糊重要度
由表4 结果可得,当根节点所处上述模糊数描述的故障状态中时,系统组件x2对叶节点即启动系统发生轻微故障的影响最大。即x2为航空涡扇发动机启动系统的薄弱环节,此时的故障排查工作可首先从电机线路是否已被烧蚀开始进行。当启动系统处于完全故障状态时,由系统中各组件重要度的大小顺序可知x4、x1和x5为启动系统的相对薄弱点,此时的故障排查工作应首先依次从检查调压器状态是否烧蚀、电机轴承是否故障和调压器是否处于失灵状态开始。
同理,由表5 可知,当启动系统处于轻微故障状态时,故障排查工作可按重要度大小顺序依次从x8、x2、x7、x5、x6、x9、x3、x4、x1开始,当发动机启动系统处于完全故障状态时,对系统各组件的故障排查工作可由重要度的大小排序x2、x3、x4、x6、x1、x9、x8、x7、x5依次开始。
2.2.4 计算根节点后验概率
在启动系统处于故障状态时,利用公式推导贝叶斯网络中根节点xi的后验概率如表6 所示。
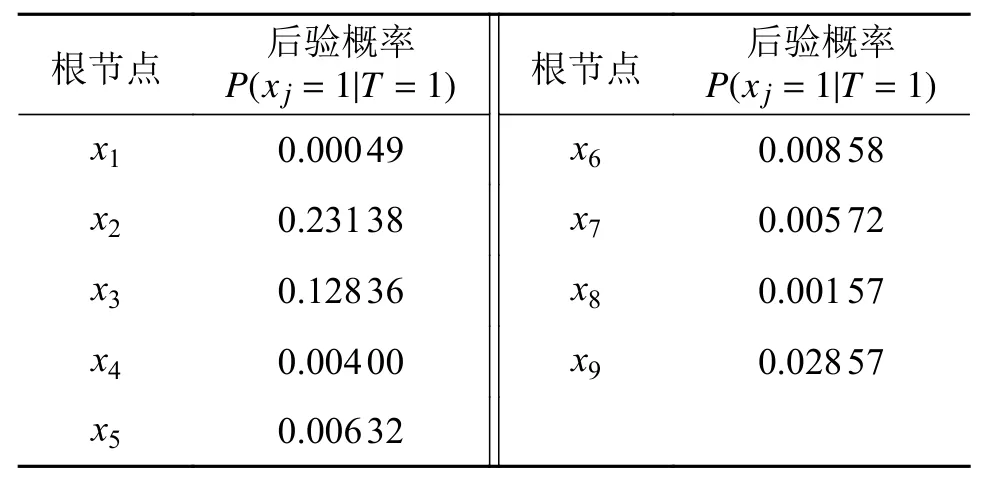
表6 根节点后验概率
由以上计算结果,当贝叶斯网络中的叶节点事件即启动系统发生故障时,后验概率从大到小依次排 序 为x9、x2、x3、x6、x5、x7、x4、x8、x1。可 知 根 节点x9的后验概率最大,说明转换器为系统的薄弱环节,其是否烧蚀对涡扇发动机启动系统的故障状态影响最大,对系统启动故障排查工作时应首先从检查转换器的健康状态开始。
3 提高涡扇发动机启动系统可靠性的几点建议
由实证分析结果,可为提高涡扇发动机启动系统的运行可靠性提供以下几点建议:
1)系统维护时,应首先对发动机启动系统的转换器和电机线路进行重点检查并记录,特别是要提前对系统转换器处于失灵或烧蚀状态及电机线路的烧蚀作好预防和维修工作的准备,以最大程度降低启动系统故障发生的可能性同时提高维修效率,从而实现维护方案的优化。
2)当涡扇发动机启动系统发生故障时,可以按照对系统中各组件重要度大小的计算结果和基本事件后验概率的排序,由大到小的进行故障排除以及维修工作。
3)为了增强航空过程中的安全性和稳定性,应提高对发动机启动系统各组件的质量要求,比如更高标准要求调压器、转换器和电机线路的质量与精度等。
4 结束语
在分析某型航空涡扇发动机启动系统部件组成及功能的基础上,将T-S 模糊故障树法和贝叶斯网络模型进行优势互补,解决系统可靠性分析模型中存在的数据精度不够和难以双向推理问题。并使用两种更具有实际应用价值的重要度分析方法,评估启动系统中各组件处于不同故障程度和故障状态时为系统带来的影响,从而建立起以此种发动机启动系统为模型的故障研究体系。
重要度和后验概率的计算结果可作为系统故障原因排除的重要参考,模型的应用将帮助进一步提升飞机运行过程中的可靠性和稳定性,并为之后启动系统的设计与维修工作指明方向。

