时序溯源的嵌入式数控系统软件可靠性研究
游达章 , ,许文俊 , ,张业鹏 ,
(1. 湖北工业大学 机械工程学院,武汉 430068;2. 湖北省现代制造质量工程重点实验室,武汉 430068)
嵌入式数控系统软件可靠性是指系统软件在已知条件下,在规定时间内运行不失效的能力,其软件失效一般是由程序设计缺陷、参数设定错误等内部缺陷引起的[1-2],如果不及时处理将会造成严重后果。
由于“前、后台”结构和系统多中断特点,以及由于插补加工轨迹的多样性,使得嵌入式数控软件程序运行路经不确定性大,各模块的运行逻辑顺序不固定,模块之间的转接具有随机性,系统软件可靠性建模困难,传统的串、并联等模型很难解决其可靠性建模问题。在数控系统可靠性研究方面,Gu 等[3]以某数控机床主轴系统为例,将概率模型检测和离散时间马尔可夫链应用于故障树分析。本文将用马尔可夫链模型来进行嵌入式数控软件可靠性的研究。马尔可夫链模型在解决系统模块结构复杂的可靠性问题上有其独特的优势,适合描述嵌入式软件各模块之间的随机运行过程,而马尔可夫链模型最重要的问题是其运行剖面及转移矩阵的准确性与定量化。
在运行剖面的生成及转移矩阵定量化的问题上,Singh 等[4]为解决马尔可夫链两种转态之间的转移概率的不确定性问题,提出了用Petri 网对软件系统进行建模的方法,将其转换为马尔可夫链来求解线性系统。华中科技大学吴军等[5]监控了数控软件的运行过程,构建了运行剖面,但是现场监测成本高,不适合初期可靠性评估。张文秀等[6]通过对风电并网系统的运行状态划分,由系统状态样本数据得到状态转移矩阵,进而构件可靠性评估模型。Calinescu 等[7]通过建立具有不确定转移概率的马尔可夫链模型,并使用两个不同领域的案例来评估定量验证技术的有效性,证明了马尔可夫链转移概率的不确定性会导致错误决策和低质量的软件系统。从文献可以看出,马氏链的运行剖面与转移概率问题非常重要,但对其生成与定量化方法介绍较少。
为解决上述问题,本文采用时序溯源的方法追踪嵌入式数控系统程序运行路径,来精确定量的构建其运行剖面和转移矩阵。结合数控系统开源程序源码GRBL,采用软件插桩[8-9]的方法来监测和采集数据,按照时间先后顺序标定数据,绘制时序图。另外,采用“插桩”进行数据监测、采集会额外占用系统的硬件资源,将影响程序运行的时间,甚至会改变模块原先的执行逻辑顺序。因此采用时间补偿的方法恢复嵌入式数控系统程序模块运行的真实逻辑关系,还原原始运行路径,保证运行剖面生成的准确性。
1 嵌入式数控系统CPU 运行时序图
嵌入式数控系统有多个功能模块,包含主任务模块、译码模块、路径预处理模块、速度规划模块、加减速模块、插补模块等,系统具有多个任务、多个中断,模块交叉运行,程序非顺序执行。其软件体系采用“前、后台”结构,译码和插补预处理等模块在后台运行,电机脉冲分配采用定时中断方式作为前台程序运行,电机驱动的定时周期随着速度的变化而变化,中断周期不固定,以此来控制步进电机的脉冲频率,控制电机转速和加速度,从而达到调速的目的,因此程序运行逻辑复杂。
而马氏链模型能够很好地解决系统具有随机性和模块化结构复杂的可靠性问题[10-11]。用马氏链模型来研究嵌入式数控系统软件的可靠性,关键在于其运行剖面的确定和转移概率的量化,因此采用时序溯源的方法来得到程序运行的逻辑顺序,绘制嵌入式数控系统的CPU 运行时序图,精确定量的构建其运行剖面和转移矩阵。
为获取嵌入式数控系统程序运行的逻辑顺序,以程序源码的一系列G 代码执行为监测周期,根据数控插补原理,采用软件插桩的方法在程序各处设置关键监控节点,主要监控译码信息、坐标信息、速度等信息,通过串口的方式将监测信息打印出来。然后以主程序运行时间为主线,结合前台中断,将采集得到的监控数据,包括系统时间、位置信息等,按照监测输出的的实时时间,标定在时间轴上,绘制CPU 运行时序图,重现运行逻辑过程。
图1是通过串口打印得到的部分监测信息,在嵌入式数控程序源码的每个功能模块处通过插桩的方式插入“printf”语句,跟踪程序模块的执行顺序,并记录程序运行的系统时间。根据得到的实时时间,将每个功能模块标定在时间轴上,绘制嵌入式数控系统的CPU 运行时序图。
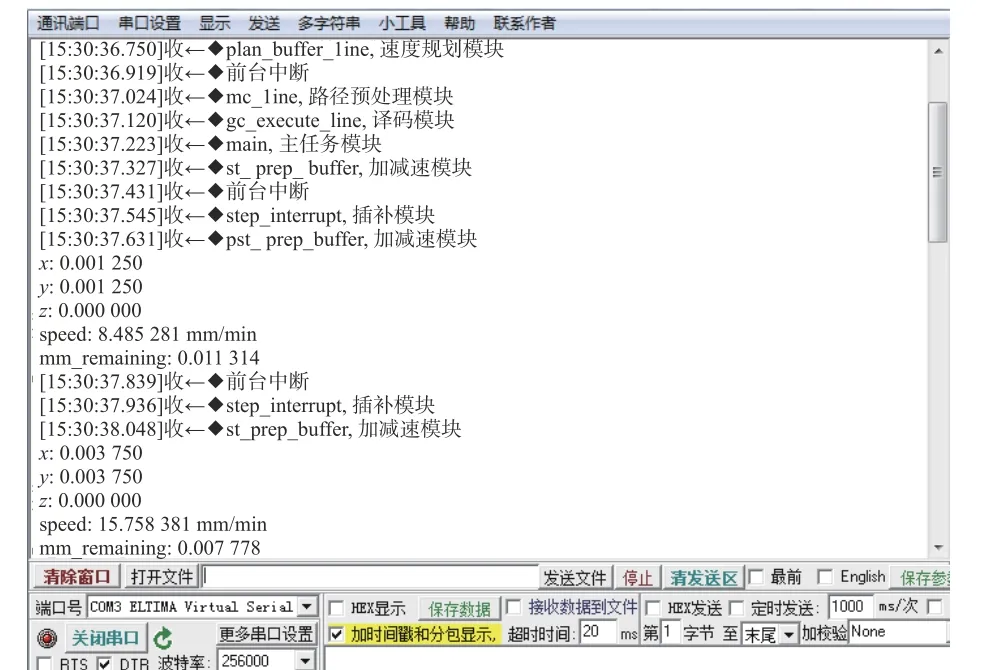
图1 串口监测信息
嵌入式数控系统的CPU 运行时序图如图2 所示,该时序图是以嵌入式数控系统程序的一系列G 代码为执行周期,将采集到的监控信息按照时间顺序标定在时间轴上。从时序图可以得到系统各功能模块运行的逻辑顺序,进而构建运行剖面和转移矩阵。但时序图中的串口输出部分影响了系统的实时性,需要还原时序图的真实逻辑顺序。
图2 CPU 运行时序图
2 还原CPU 在时间轴上的逻辑顺序
在时序溯源过程中,最关键问题是监测点的数据采集时间在时间轴上相对于真实位置的偏移问题,仿真环境下嵌入式系统的监控及信号的采集一般采用串口等硬件资源输出,产生了额外的时间开销,影响了系统执行的实时性,造成监测点对应语句执行时间将会在系统时间轴上漂移,滞后程序原本的执行时间,可能会将影响定时中断在系统时间轴上发生的位置,甚至会改变模块之间执行的顺序。因此必须定量嵌入式软件仿真运行环境下数据监测、采集对系统运行时间的延滞量,累积叠加插补周期内监测数据输出所消耗时间,采用时间补偿、延长定时中断等方法来消除其对系统程序运行路经和时序顺序的改变,复原软件运行的正确逻辑关系,重溯CPU 真实运行的时序图。
为了获得系统各功能模块真实运行的逻辑顺序,以单步调试方式获取在仿真环境下“插桩”等用于测试程序语句所运行时间。假设前台主程序通过六个串口输出监测数据,通过仿真测试,测得每个串口输出(sprintf)产生的延迟时间ti(i=1,2,…,6),若无串口输出,则延迟时间ti=0。
引入状态变量 λi来标记每个模块的串口输出状态,表达式为
即在一个大周期循环内,某个中断发生时间在时间轴上的偏移量为
由此,以大周期为循环单位,增加前台中断时间周期,调整时间轴上中断发生的相对位置,还原程序运行的逻辑顺序。调整后的中断定时时间为
式中:T2为调整后的中断定时时间;T1为理论中断时间。最后,验证改进之后的程序,通过在线仿真观察中断响应与原逻辑顺序对比分析,验证其一致性,通过不断调整,使之符合真实逻辑运行关系。
程序执行逻辑调整示意图如图3 所示。图3 中Ⅰ是实测第N周期的CPU 运行时序示意图,包括后台主程序、前台中断和串口输出等信息,由于在程序中使用了串口输出,产生了额外的时间开销,图中的前台中断在时间轴上产生了漂移(理论在插补模块中的前台中断向前漂移到了加减速模块)。为了还原前台中断在时间轴上的真实位置,采用时间补偿的方法,增加前台中断在时间轴上的时间,得到改进后的第N周期示意图Ⅱ。最后,去掉时序图Ⅱ中的串口输出部分,得到理论第N周期示意图Ⅲ,即CPU 真实运行的逻辑顺序。
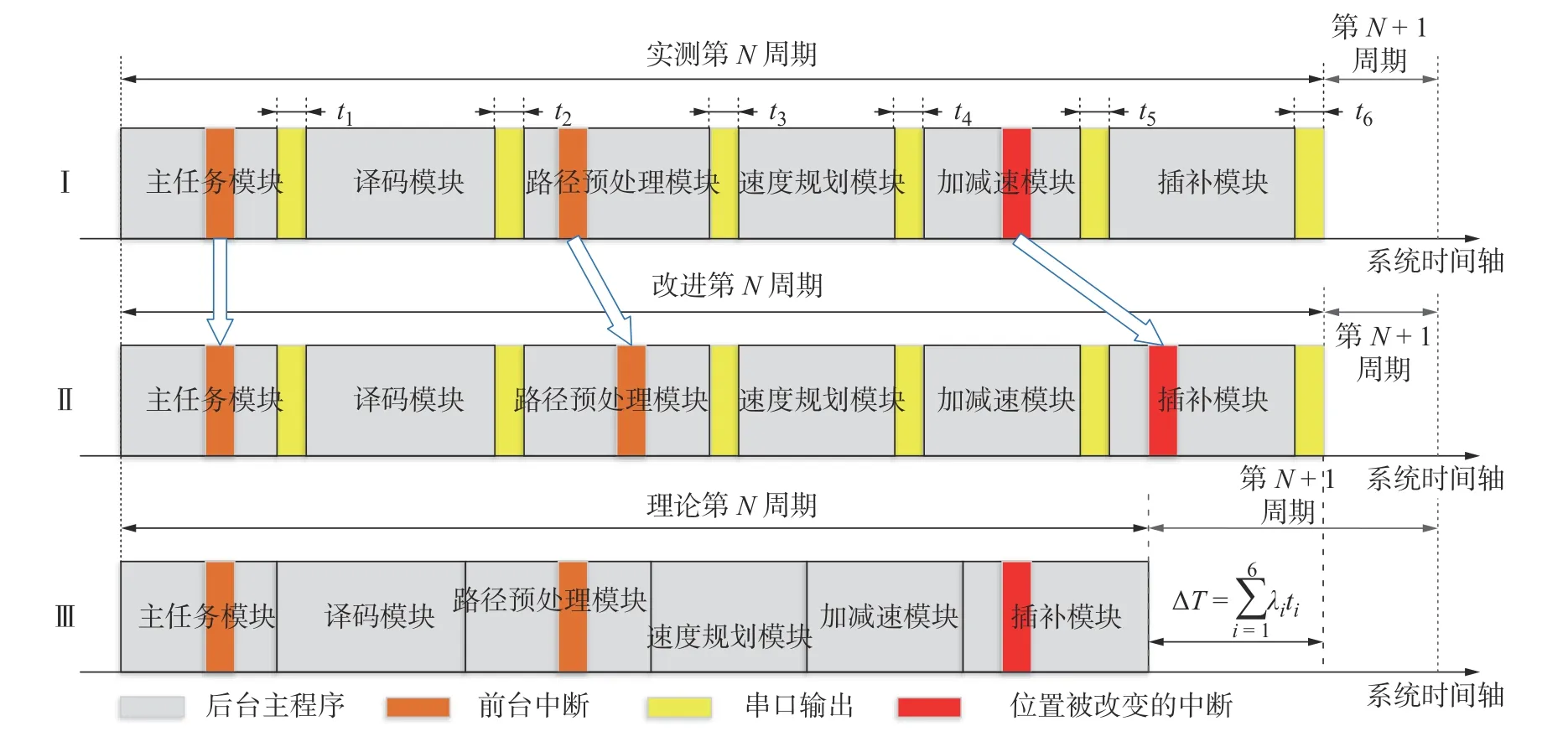
图3 程序执行逻辑调整示意图
3 运行剖面下的马尔可夫链可靠性建模
3.1 马尔可夫链建模方法
根据第2 节调整后的时序图谱,建立插补程序运行剖面,统计模块相互之间的转移概率;根据监测的大数据及故障识别结果,计算模块可靠度及模块转接失效率,构建运行剖面和转移矩阵,建立基于运行剖面的Littewood Markov 链模型。建模时考虑基于加权系数的模型改进优化,对马尔可夫模型进行了改进,引入了单一模块运行时间占系统总时间比例,通过加权机制来优化模型,减少因统计误差带来的精度扰动。
3.2 马尔可夫链基本概念
马尔可夫链可以用来研究嵌入式数控系统中的各个功能模块的可靠性和相互关系。马尔可夫链是一个随机过程,它在时间和状态上都离散,是一个典型的马尔可夫过程[12]。
设有一个随机过程 {X(t),t∈T}, 其中X(t)表示在时间t时刻的状态,T表示离散时间的集合,其离散状态的集合A={a1,a2,a3,···} 。 若对任意整数n∈T和任意a1,a2,···,an∈A,条件概率满足
则称{xn,n∈T}是马尔可夫链。马尔可夫链具有无后效性,即系统下一次的状态只与当前状态有关,而与上一次以及之前的状态无关[11,13]。条件概率P{xn=j|xn-1=i}表 示系统在时刻n-1处 在状态i条件下,在n时刻系统从状态i转移到状态j的概率,称此概率是马氏链的转移概率,也称一步转移概率,记为pij(n)。 转移概率pij(n)一般可以构成转移概率矩阵,可表示为
其中
3.3 改进的Littewood Markov 链模型
建立模型时,考虑嵌入式数控系统中某一个模块运行时间占整个嵌入式数控系统运行时间的比例,对马尔可夫模型进行了改进,引入了单一模块的运行时间占系统总时间比例。
假设嵌入式数控系统中的模块数量为N,模块转移序列为x1,x2,···,xn,上一次模块与下一次模块之间的转移次数构成模块转移矩阵K为
式中kij为 系统上一次模块状态为i,而接下来的模块状态为j的模块转移次数。由系统从模块i转移到模块j的转移概率pij(n)可 得到转移概率矩阵P为
其中转移概率为
嵌入式数控系统在运行中会伴随着软件程序错误,出现模块之间的失效,在Littewood Markov 链模型中模块的失效是相互独立的,每新增一个模块,都将引入新的错误,这种错误来源于模块的泊松失效过程[14]。设模块 λi为 模块i的泊松失效率,用行向量表示为 λ =[λ1,λ2,···,λi],qi j为系统中从功能模块i转移到功能模块j失效的概率
令ti为 系统第i个模块运行的时间,模块运行时间序列T=[t1,t2,···,ti]。ki为系统第i个模块的运行时间占整个系统运行时间的比例
在Littewood Markov 链模型中,程序的失效过程接近于泊松分布,改进的Littewood Markov 链模型中引入了时间加权系数,其失效率为
3.4 实例步骤
步骤1 在测试阶段,记录嵌入式数控系统各功能模块的运行顺序,得到模块运行序列x1,x2,···,xn,即可得到模块转移概率矩阵P和模块的运行剖面,同时记录测试阶段发生故障的模块种类以及发生故障的次数,即可得到模块失效率 λi。
嵌入式数控系统调整后的CPU 时序图谱如图4 所示,各功能模块的运行序列由时序图谱获得。为方便表示,将各个功能模块用数字序号代替,如表1 所示。

表1 各功能模块对应数字序号

图4 调整后的CPU 运行时序图
则由嵌入式数控系统的时序图得到模块的运行序列为:17 123 474 321 575 656 575 656 765 651,根据模块的运行序列来计算各模块之间转移的次数,得模块转移矩阵K为
由模块转移矩阵得到模块转移概率矩阵P为
因此,模块的运行剖面如图5 所示。

图5 模块运行剖面图
测试过程中测得每个功能模块运行的失效次数fi和 总的运行次数ni,可得到各个模块的失效率计算得到的模块失效率向量为
步骤2 在记录模块运行顺序的同时,也需要记录各个模块的系统运行时间ti。并测试出软件运行的总时间,计算系统第i个功能模块的运行时间占系统整体运行时间的比例ki。各功能模块的运行时间及比例如表2 所示。

表2 各功能模块的运行时间及比例
步骤3 当测试结束时,统计从模块i转移到模块j失效的概率,得到模块失效概率矩阵Q为
步骤4 计算得到嵌入式数控系统的整体失效率F为
4 结论
1)嵌入式数控系统的可靠性至关重要,本文结合马尔可夫链进行研究,构建了嵌入式数控软件运行剖面及转移矩阵,建立了马氏链的可靠性评估模型。为嵌入式软件故障分析、诊断、可靠性评估提供理论和技术支撑,可以推广运用于嵌入式软件调试、测试、分析设计等方面。
2)传统的马氏链模型的转移矩阵和运行剖面一般通过经验、或者统计得到,准确性很难保证。较以往不同,本文提出时序溯源的方法来追踪嵌入式数控系统程序运行路径,使构建运行剖面及转移矩阵定量化。该方法很适合模块化结构复杂的系统,使可靠性建模更精确。
3)时序溯源中采用了软件插桩的方法来获取监测数据,通过串口等硬件资源输出将影响系统执行的实时性。因此提出了时间补偿的程序运行逻辑恢复方法,采用延长定时时间来恢复原本运行逻辑顺序,还原原始运行路径,保证了运行剖面生成的准确性。
4)本文通过时序溯源的方法建立了马氏链的可靠性评估模型,最后对马尔可夫链模型进行了改进,引入功能模块时间占比的加权系数,通过加权机制来优化模型,减少由于统计误差带来的系统评估精度扰动。

