采用统一性能衰退轨迹模型的润滑和密封材料加速寿命预测
吕向飞 , ,陈进
(1. 重庆大学 机械传动国家重点实验室,重庆 400044;2. 重庆电子工程职业学院 智能制造与汽车学院,重庆 401331)
润滑与密封材料是机械设备中应用最为广泛的两种材料,润滑和密封的性能优劣直接影响机械设备的使用性能,并极大程度上影响了设备的运行维护和保养成本。因此,对润滑和密封材料的老化寿命进行快速准确的评估,有助于提升润滑和密封材料的优化设计周期,并为制定科学合理的机械润滑与密封的维护保养提供理论依据。现有润滑和密封材料加速寿命方法研究中,按研究内容,可分为性能衰退指标研究,新型加速模型研究和基于Arrhenius模型的应用研究3 个方面。
在性能衰退指标研究方面,文献[1]在分析了橡胶热空气老化的化学机理的前提下,应用热空气加速老化,获得了橡胶的性能衰退数据,以压缩永久变形为衰退指标,推算出了常温下橡胶的使用寿命。文献[2]结合红外光谱分析等手段,确定出密封橡胶老化的失效评价指标,并在高温加速试验数据的基础上,由Arrhenius 模型对常温下的寿命进行准确计算。文献[3]以压缩永久变形为性能衰退指标,对密封橡胶进行了不同温度下的老化试验,并通过Arrhenius 模型,由高温下的性能衰退轨迹推算出常温下的性能衰退规律,对常温下的使用寿命进行科学的推断。文献[4]在传统加速老化试验的基础上,提出压缩永久变形和压缩应力松弛双失效指标,对O 型密封橡胶的寿命和可靠性进行了更为准确的评估。文献[5]提出了以接触应力为密封橡胶的性能衰退指标,通过加速老化试验,对橡胶密封的使用寿命进行了更为精确的预测。文献[6]同时考虑压缩永久变形和压缩应力松弛两个性能衰退指标,采用二元时变Copula 模型建立起丁腈密封橡胶性能衰退的多元性能衰退的加速模型,对橡胶的可靠性进行了更为准确的评估。文献[7]同时考虑应变、应变能和应力等参数,提出了一种新型损伤参量,用于描述多轴橡胶疲劳寿命。综上所述,对于不同应用场景下的润滑和密封零部件,不存在普适性的指标,应根据实际应用场景,选取最为合适的性能衰退指标作为所研究对象寿命预测的性能衰退评价指标。
在新型加速模型研究方面,文献[8]提出应用插值的方法获得不同温度下老化橡胶的伪失效寿命,在此基础上,应用时温等效原理计算出各加速温度下的加速因子,并应用Arrhenius 模型由高温加速因子推算出常温下的加速因子,从而对常温下的老化寿命进行可靠的预测。文献[9]应用Eyring 模型建立了温度和湿度双应力同时作用下加速模型,对硅橡胶在湿热老化环境下的寿命进行了准确评估。文献[10]建立润滑脂寿命与温度之间的二次函数关系式,对轮毂轴承的润滑脂寿命进行了准确的评估。文献[11-12] 同时考虑辐射和温度对橡胶老化的影响,建立橡胶在辐射和高温综合作用下的等效加速模型,对综合老化因子进行了预测。综上所述,现有加速模型的研究正不断从单应力模型向多应力模型发展,建模方法也在Arrhenius 模型的基础上出现一些改进或替代模型,Arrhenius 模型的适用性须在工程实际应用中得到进一步的验证。
在基于Arrhenius 模型的应用研究方面,文献[13]通过不同温度下的加速老化试验,获得某轴承用有机硅润滑脂的性能衰退数据,在分别对各加速温度下的数据进行轨迹建模的基础上,根据Arrhenius 定律推算出了常温下的性能衰退轨迹,对常温下的性能衰退进行了准确评估。文献[14]建立二硫化钼锂基润滑脂的老化性能衰退轨迹模型,通过3 个不同高温下的老化试验获得的加速试验数据,在Arrhenius模型的基础上对常温下的老化寿命进行了评估。文献[15]在Arrhenius 模型的基础上,提出几种加速因子的计算方法,促进了Arrhenius 模型的工程推广应用。文献[16]在加速试验数据的基础上,采用Arrhenius 模型,对两种橡胶的贮存寿命进行了准确预测。综上所述,现有加速方法在Arrhenius 模型的基础上,已经形成了较为完整的寿命预测体系,但润滑与密封的加速衰退轨迹建模和寿命评估方面的研究仍有望进一步的深入探索,为更为快速准确的寿命预测和可靠性评估提供理论支撑。
有鉴于此,本文针对传统加速寿命评估方法中采用的分步数据处理和参数分步拟合造成的数据总体精度无法保证和参数识别效率较低的问题,在传统Arrhenius 模型的基础上,提出了统一性能衰退轨迹模型,通过时间尺度的幂指数缩放,提高建模的精度,将所有加速数据统一用于衰退轨迹建模,在提高精度的同时保证了效率。
1 统一性能衰退轨迹模型
传统的动力学模型方法在处理润滑与密封材料加速试验数据时,常采用分步处理的方法,分别对各个加速温度下的数据进行处理,获得各温度下的性能衰退方程;在此基础上,假设方程系数服从Arrhenius定律,通过拟合外推由高温下的方程系数获得常温下方程系数。此方法将各加速温度下的数据割裂处理,未能充分利用整体数据进行拟合,可能存在某一温度下数据的异常,而造成整体加速系数拟合较差,因此该方法的抗干扰能力较弱,且流程过于繁琐。
为解决传统方法所具有的弊端,本文提出图1所示的性能衰退轨迹统一建模方法。所提出的性能衰退轨迹统一建模方法的优势在于:直接对所有温度下的性能退化数据加以利用,在统一的模型下进行参数辨识,避免各温度下数据分开拟合异常值对结果可能造成的干扰,同时统一参数辨识方法在减少模型参数辨识次数的同时,由于取消了由各温度下的轨迹方程参数对加速模型参数进行识别的二次参数辨识过程,也能够在一定程度上提高参数识别的精度。

图1 统一性能衰退轨迹建模方法流程图
式中:y(t,T)为 所提出的性能衰退量函数模型;k1、k2和k3为 常数;t为老化时间;T为加速温度; β为时间尺度因子;通过 β将时间进行非线性幂尺度变换,提高拟合精度。
式中: m ax(·) 为取最大值函数;yt为实测性能衰退值;R(·)为相关系数函数,相关系数函数的表达式为
在获得最优的时间尺度因子 β后,以式(4)所示的均方误差MSE 最小化为目标,对式(1)中的3 个模型参数进行辨识。
式中:EMS为 均方根误差;yti为 第i个实测性能衰退量;yi(t,T)为 第i个预测的性能衰退量。
通过最小化均方误差获得统一性能衰退模型中的参数数值后,可获得加速方程为
性能衰退速率kv表征的是性能衰退的快慢。由式(5)可知,本文中认为衰退速率与加速温度的倒数之间满足指数关系,即符合Arrhenius 定律。
根据式(5)可由高温下的加速速率外推获得常温下的加速速率,在本文中,建立了统一性能衰退轨迹模型后,可不必由式(5)的外推获得常温的衰退速率,但由式(5)可推算出润滑或密封材料的活化能,活化能的计算公式为
式中:Ea为活化能,kJ/mol;R为理想气体常数,通常取R=8.314 J/(mol·K-1),通过活化能可以对比不同材料的抗老化能力,一般活化能的绝对值越大的材料,其抗老化能力越强。
2 实例分析
为验证本文所提出的时间尺度因子优化的统一性能衰退轨迹模型建模的有效性,分别以文献[13]中的润滑脂加速性能衰退数据和文献[3]中的密封橡胶加速性能衰退数据为例,进行加速老化寿命建模,并预测时间-温度-性能衰退量之间的三维关系。
2.1 润滑脂加速寿命建模
文献[13]中给出了某有机硅润滑脂的加速老化性能衰退试验数据,试验温度分别为90 ℃、105 ℃、120 ℃和135 ℃,总的老化时间为90 d,检测的时间点共有8 个,非等间隔。
图2所示为润滑脂性能衰退数据建模中,拟合优度指标(相关系数),随时间尺度因子 β的变化关系,由图2 可知,当β =0.13时,相关系数取得最大值。
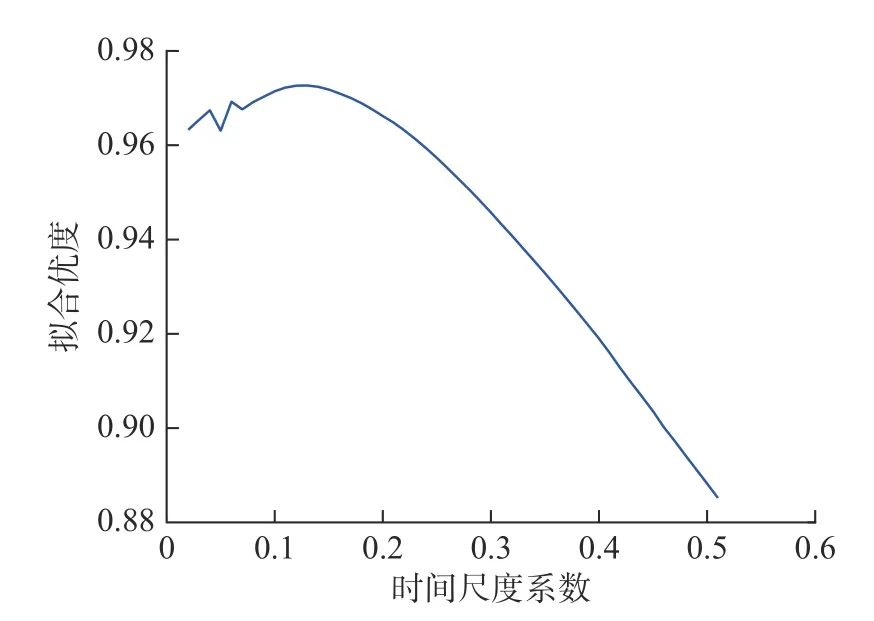
图2 润滑脂退化轨迹的时间尺度因子与拟合优度
图3所示是各不同温度下的润滑脂性能衰退量随时间的变化曲线的对数图。图3 中,散点为实测数据,实线为预测数据,55 ℃的数据为由统一模型外推获得的常温下的数据。由图3 可知,90 ℃、105 ℃和135 ℃的数据拟合效果较好,而120 ℃数据拟合效果较差,说明120 ℃数据存在误差。若直接使用传统的分步建模方法,分别针对每一加速温度下的数据进行拟合,虽然能够取得各组衰退轨迹的最优拟合效果,但无法在轨迹拟合过程中仍保证Arrhenius模型的约束,导致异常数据的误差将被放大,从而影响整体的建模精度。在统一建模方法中,参数辨识统一在式(1)中完成,而传统方法在各温度下轨迹建模获得的不同温度下的性能衰退速率基础上,再通过式(5)所示的Arrhenius 方程进行各温度下的速率拟合,从而外推获得常温下的衰退速率;传统方法的误差放大主要由于在传统方法中,式(5)中的衰退速率样本点是由带误差的样本点分别各自拟合得到,未充分应用整体数据对个别误差进行平均消除。因此,应用统一模型的建模方法,不仅在统一模型中保证了Arrhenius 模型的约束,且时间尺度因子能够针对整体数据求得全局最优解,这样所有样本点的误差都将得到整体的平均抑制,从而使得模型的建模精度有所提升。
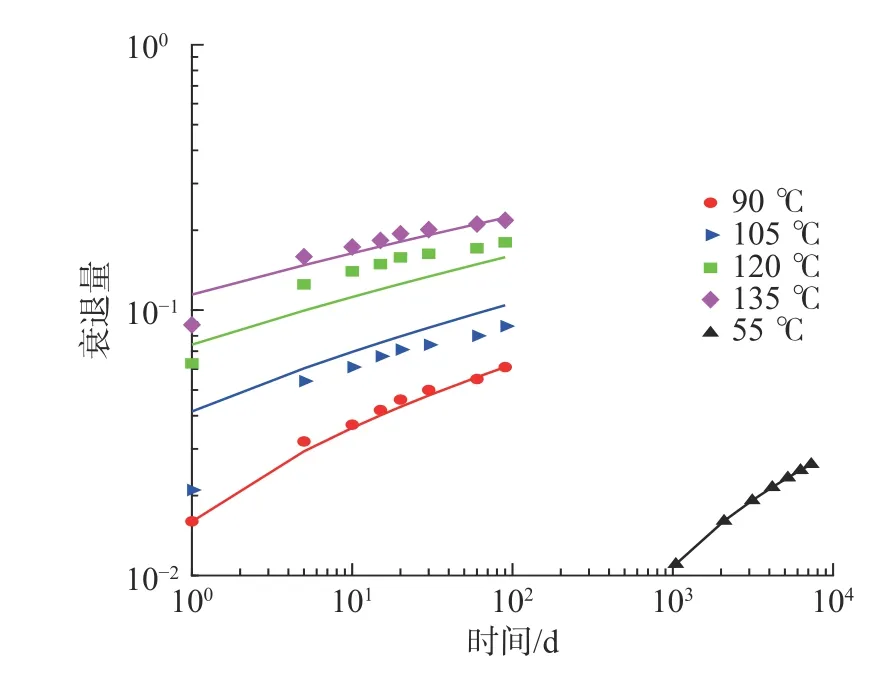
图3 润滑脂衰退量实测数据与预测结果对比
为了进一步获得统一性能衰退轨迹模型中速率函数的规律,根据式(5)得到润滑脂各温度下的性能衰退速率随温度倒数的曲线图,由图4 可知,润滑脂性能衰退速率在对数图上,与温度倒数呈现很好的直线关系,说明润滑脂性能衰退速率满足Arrhenius定律,统一模型建模的Arrhenius 机理假设得到了验证。在速率-温度图的基础上,由式(6)计算得到的润滑脂的老化活化能为28.08 kJ/mol。

图4 润滑脂衰退速率随温度的变化
图5所示是由所建立的统一模型作出的时间-温度-性能衰退量之间的三维关系图,图5 中,散点为实测性能衰退数据,由散点与曲面的吻合程度可知,所建立的统一性能衰退模型,能够很好的预测不同温度下、经过不同时间老化的润滑脂的性能衰退量,由统一模型我们可进一步对常温下的性能衰退量随时间的变化关系进行准确的预测。
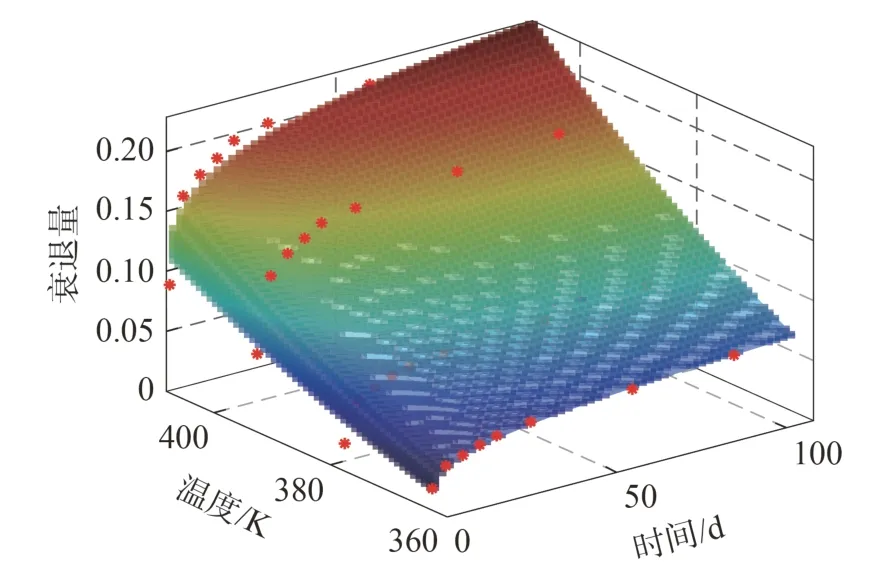
图5 润滑脂时间-温度-衰退量的预测效果
2.2 密封橡胶加速寿命建模
文献[3]中给出了某O 型橡胶密封圈的加速老化性能衰退试验数据,试验温度分别为100 ℃、110 ℃、120 ℃、130 ℃和140 ℃,共5 组不同温度下的性能衰退数据,总的老化时间为143.5 d,每个温度下的检测的时间点为9 ~ 16 不等,且各检测点间非等间隔。
图6所示为密封橡胶性能衰退数据建模中,拟合优度指标,即相关系数,随时间尺度因子 β的变化关系,由图6 可知,当 β=0.56时,相关系数取得最大值。

图6 密封橡胶退化轨迹的时间尺度因子与拟合优度
图7所示为各不同温度下的O 型密封橡胶性能衰退量随时间的变化曲线的对数图。图7 中散点为实测数据,实线为预测数据,45 ℃的数据为由统一模型外推获得的常温下的数据。由图7 可知,110 ℃、120 ℃和140 ℃的衰退数据拟合效果较好,而100 ℃和130 ℃数据有部分样本点的拟合效果较差,说明100 ℃和130 ℃数据存在误差。通过统一模型建模,100 ℃和130 ℃样本点中老化后期的几个样本点的误差实现了整体平均而有效抑制了,这样使得整体建模精度有所提升。关于异常点数据带来的误差如何通过统一建模而抑制在上文对图3 的分析中已说明,此不赘述。
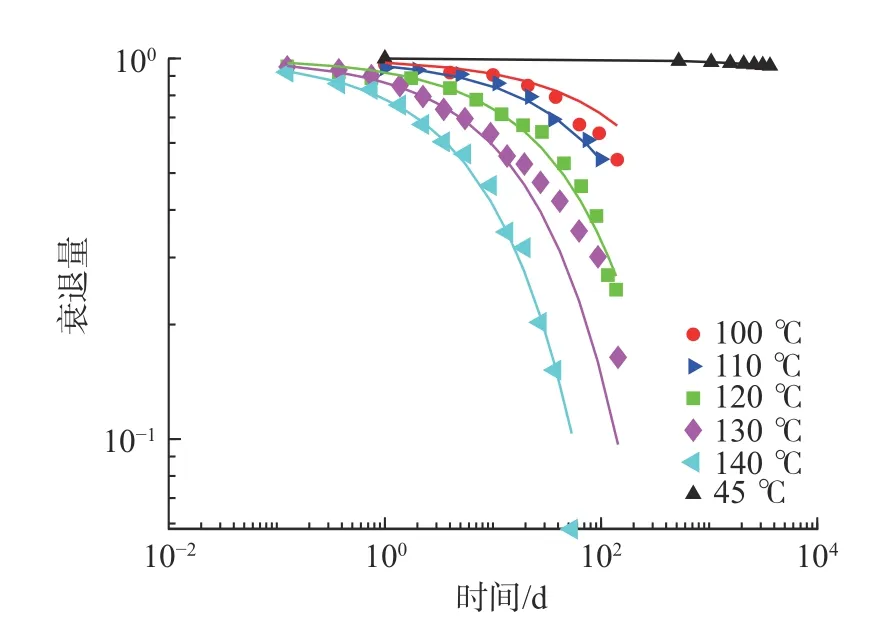
图7 密封橡胶衰退量实测数据与预测结果对比
为了进一步获得统一性能衰退轨迹模型中速率函数的规律,根据式(5)得到O 型橡胶密封圈各温度下的性能衰退速率随温度倒数的曲线图,如图8所示。由图8 可知,O 型橡胶密封圈性能衰退速率在对数图上,与温度倒数呈现很好的直线关系,说明性能衰退速率满足Arrhenius 定律,密封橡胶的性能衰退速率的Arrhenius 机理假设得到了验证。在速率-温度图的基础上,由式(6)计算得到的润滑脂的老化活化能为72.51 kJ/mol。
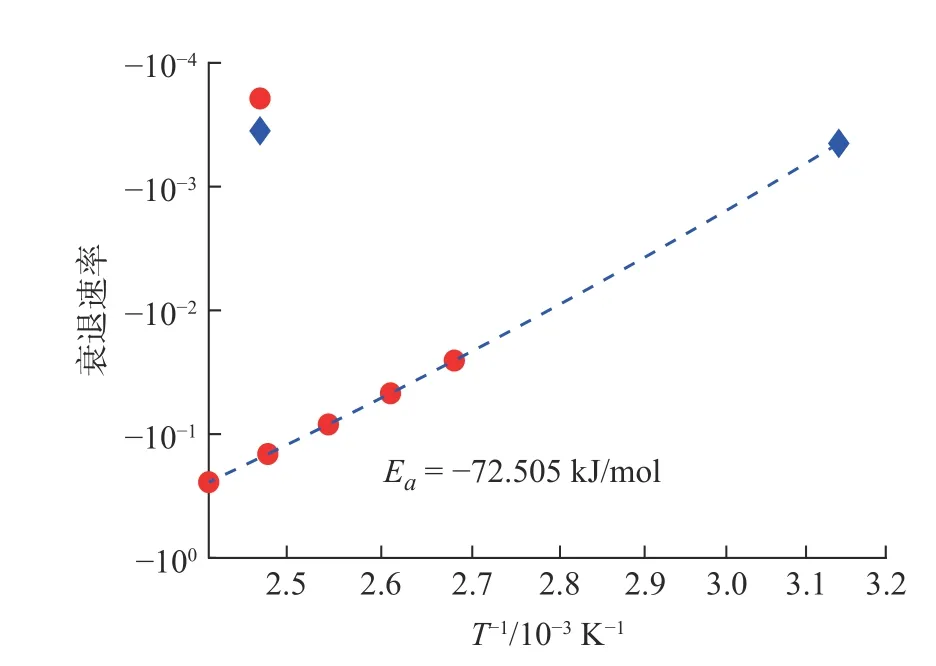
图8 密封橡胶衰退速率随温度的变化
图9所示为由所建立统一模型做出的时间-温度-性能衰退量之间的三维关系图。图9 中,散点为实测性能衰退数据,由散点与曲面的吻合程度可知

图9 密封橡胶时间-温度-衰退量的预测效果
,所建立的统一性能衰退模型,能够很好的预测不同温度下、经过不同时间老化的O 型橡胶密封圈的性能衰退量,由统一模型我们可进一步对常温下的性能衰退量随时间的变化关系进行准确的预测。
3 结论
1)提出时间尺度优化的加速退化轨迹统一模型,对不同老化时间,不同加速温度下的性能衰退轨迹数据进行准确预测。
2)分析模型中的衰退速率,发现衰退速率很好的满足Arrhenius 指数衰退定律,并结合实际性能衰退数据阐明了模型中参数的物理意义。
3)在实测加速老化数据的基础上,分别由所提出的方法建立润滑脂和密封橡胶加速寿命的预测模型,对常温下的使用寿命进行快速而准确的评估。
4)通过对比润滑脂和密封橡胶的活化能,可知,密封橡胶的活化能绝对值远大于润滑脂,说明密封橡胶的抗老化能力远大于润滑脂。

