具有多工作模式的电机式主动横向稳定器控制策略研究
张旗,严天一,赵燕乐
(青岛大学 机电工程学院,山东青岛 266071)
当车辆在弯道或不平路面行驶时,侧倾角控制合理与否可直接影响乘坐舒适性和安全性,当侧倾角过大时,极易引发重大交通事故。为此,绝大多数车辆安装有传统被动横向稳定杆,以减小车身侧倾角,但被动横向稳定杆因其扭转刚度为常值,且所产生的反侧倾力矩不可实时调节,故其抗侧倾作用尚不够理想。主动横向稳定器(Active anti-roll stabilizer,AAS)可根据不同行驶工况对车身侧倾刚度自动调整,可实现较大范围的可变反侧倾力矩输出,其抗侧倾效果明显优于传统被动横向稳定杆[1]。
目前,AAS 主要包括液压式主动横向稳定器(Hydraulic active anti-roll stabilizer,HAAS)与电机式主动横向稳定器(Electric active anti-roll stabilizer,EAAS)。陈山[2]设计了HAAS 分层控制算法及其电子控制单元,并开展了新型控制算法的半实物仿真研究,相关结果表明,该控制算法可提高车辆侧倾稳定性。赵福民[3]提出器HAAS 线性化反馈的滑膜控制策略,实车试验表明所该控制算法可显著改善车辆抗侧倾特性。周兵等[4]通过构建包含主动横向稳定杆的主动悬架整车动力学仿真模型,并根据两者之间的耦合关系,设计了AAS 新型集成控制策略。陈祥林等[5]提出AAS 模糊滑模控制器,并进行了相关仿真实验验证。Zulkkarnain 等[6]为深入研究AAS 对车辆平顺性和操纵稳定性影响效果,利用四自由度半车模型开展了相关仿真验证。Muniandy 等[7]提出自调整AAS 模糊PI-PD 控制算法,可克服传统控制算法技术缺点,有效改善整车抗侧倾性能。白先旭等[8]采用磁流变半主动横向稳定杆控制车辆抗侧倾性能,并将其与传统被动横向稳定杆进行了对比分析。李姣等[9]提出EAAS 多模式控制算法,其可根据不同行驶工况选择相应的工作模式,可有效提升车辆侧倾稳定性。Suzuki 等[10]开发了带有谐波齿轮减速器的EAAS,并通过实车试验测试出其能耗性能,试验结果表明EAAS 能耗仅为相同性能HAAS 的1/20。Sorniotti[11]通过开展半实物仿真试验与实车试验,表明EAAS 可明显改善车辆侧倾稳定性。综上所述,传统EAAS 控制模式较为单一,为满足不同类型驾驶员对EAAS 动态响应特性的差异性需求,亟待开展具有多工作模式的EAAS 控制方法研究。
本文首先利用搭建具有EAAS 的整车动力学仿真模型,然后构建具有多工作模式的EAAS 模糊控制策略,并分别开展各个工作模式的离线仿真及半实物仿真,以验证具有多工作模式的EAAS 模糊控制策略的有效性。
1 理论模型构建及验证
为验证具有多工作模式的EAAS 模糊控制策略,利用MATLAB/Simulink 构建具有EAAS 的整车动力学仿真模型[12]。
1.1 整车动力学理论模型构建
采用的九自由度整车动力学理论模型由车身的垂向模型、侧向模型、俯仰模型、侧倾模型、横摆模型及车轮垂向运动模型等组成,如图1 ~ 图3 所示。

图1 整车动力学模型

图2 侧向、横摆模型
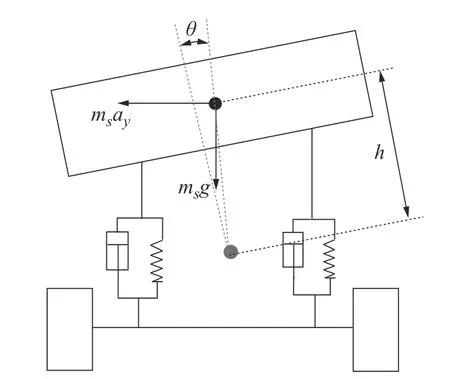
图3 侧倾模型
车身垂向模型为
簧下质量垂向模型为:
侧向模型为
俯仰模型为
侧倾模型为
横摆模型为
各悬架的簧上质量位移满足如下关系:
式中:m为整车质量,kg;ms为簧上质量,kg;mui(i=fl,fr,rl,rr)为簧下质量,kg;θ为车身侧倾角,rad;φ为车身俯仰角,rad;r为横摆角速度,rad/s;δ为前轮转角,rad;Iθ、Iφ、Ir分别为车身的侧倾、俯仰、横摆转动惯量,kg·m2;a、d为质心至前后轴的距离,m;bs为轮距,m;h为车身的侧倾半径,m;xc为簧上质量的质心位移,m;xsi为各悬架的簧上质量位移,m;xui为各簧下质量位移,m;Mf、Mr分别为前后EAAS 控制扭矩,Nm;Fi为悬架对车身的垂向力,Fi=ki(xsi-xui)+ci(x˙si-x˙ui),N;ki为各悬架的弹簧刚度,N/m;ci为各悬架的减振器阻尼,N·s/m;Foi为车轮动载,Foi=kti(xui-xoi),N;xoi为路面不平度激励,m;kti为轮胎刚度,N/m;Fyi为车轮所受侧向力,N;Vx为质心纵向速度,m/s;Vy为质心侧向速度,m/s。
1.2 轮胎模型
为准确描述轮胎在转向工况下的各力学特性,本文采用“魔术公式”轮胎模型预测轮胎侧偏力。若外倾角γt= 0,水平方向的偏移Sh= 0,垂直方向的偏移Sv= 0,则此轮胎模型[13]为
式中:Fyi(i=fl,fr,rl,rr)为各车轮所受侧向力,N;μ为路面的附着系数;αi(i=fl,fr,rl,rr)为轮胎的侧偏角,rad;B、D、E均与车轮所受载荷有关。
1.3 路面模型
本文采用四轮非平稳时域模型[14],其模型可表示为:
式中:q1、q2、q3及q4分别为左前轮胎、右前轮胎、左后轮胎及右后轮胎的路面不平度,m;x1、x2分别为状态变量;f0为下截止频率,Hz;v为车速,m/s;n0为标准空间频率,m-1;G0为路面不平度系数,m3;ω(t)为均值为0 的高斯白噪声;bs为轮距,m;l为轴距,m。
1.4 EAAS 理论模型
本文所述新型EAAS 主要包括谐波齿轮减速机构、三相无刷直流电机、左横向稳定半杆、右横向稳定半杆、霍尔传感器、壳体等,如图4 所示。内嵌电机输出的电磁转矩经谐波齿轮减速机构降速增扭后,分别传递至左、右横向稳定半杆,使EAAS 输出实时调节的反侧倾力矩,以提升侧倾稳定性,如图5所示。

图4 EAAS 结构简图
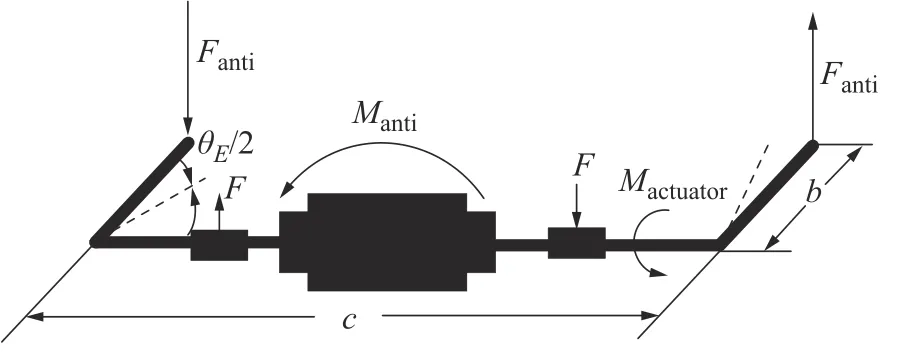
图5 EAAS 受力图
电机作动器的输出转矩与反侧倾力矩之间的关系为
式中:Mactuator为输出力矩,Nm;Manti为反侧倾力矩,Nm;b为左、右横向稳定半杆的力臂长度,m;c为EAAS 的长度,m;θE为左、右横向稳定半杆臂的相对转角,定义θE/2 为稳定半杆臂与水平面夹角,(°);F为橡胶支座对横向稳定半杆的作用力,N。
EAAS 内嵌的三相无刷直流电机定子绕组采用星型接法,三相定子绕组相电流之间的关系为
故三相无刷直流电机理论模型可表示为
式中:ua、ub、uc为定子绕组相电压,V;ia、ib、ic为定子绕组相电流,A;L、M为定子绕组的自感和互感系数,H;R为定子绕组阻值,Ω;ea、eb、ec为定子绕组相反电动势,V。
内嵌电机输出的电磁转矩为
内嵌电机转子的运动方程为
令谐波齿轮减速机构的传动比为i,则EAAS输出力矩为
式中:ω为电机角速度,rad/s;Te为内嵌电机的电磁转矩,Nm;Tl为电机负载转矩,Nm;B为电机阻尼系数,Nm·s/rad;J为电机转子转动惯量,kg·m2。EAAS内嵌电机部分参数如表1 所示。

表1 EAAS 内嵌电机部分参数
为保证建模的可靠性,本文利用CarSim 车辆仿真软件对不含EAAS 模型的整车动力学理论模型进行了相关验证。
2 EAAS 模糊控制策略
2.1 控制策略的制定
首先,利用左右车身高度传感器、车速传感器、侧向加速度传感器、转向盘角度传感器等采集车身运动状态,然后将上述信息输入至电子控制单元,并根据采集到的信号判断出此时车辆所处行驶工况,从而选择不同的控制策略使EAAS 处于合适的工作状态[9]。
1)若电子控制单元检测到的前后桥车轮左右高度差的绝对值均大于或等于5 mm,且侧向加速度|ay| ≥ 0.05 g 时,则可判定车辆正处于转弯状态,此时采用控制策略一。
2)若电子控制单元检测到的前后桥车轮的左右高度差的绝对值均小于5 mm,且侧向加速度|ay| <0.05 g 时,则可判定车辆在水平良好的路面上直线行驶,此时采用控制策略二。
3)若电子控制单元检测到的前后桥车轮左右高度差的绝对值均大于或等于5 mm,且侧向加速度|ay| < 0.05 g 时,则可判定车辆在左右不平的路面上直线行驶,此时采用控制策略三。
4)若电子控制单元检测不到状态信号,表征已发生故障,此时采用控制策略四。
2.2 各种控制策略
2.2.1 控制策略一
当车辆在转弯时会引起车身侧倾,如果侧倾角过大会降低乘坐舒适性,并导致驾乘人员紧张;反之若侧倾角过小则不利于驾驶员正确感知车身运动姿态[15-16]。为满足不同驾乘需求,本文所提出的控制策略下分别设定了3 种典型工作模式:正常模式、运动模式和柔顺模式,各模式的目标侧倾角与侧向加速度关系如下:
1)正常模式
2)运动模式
3)柔顺模式
3 种模式的目标侧倾角和侧向加速度关系响应曲线如图6 所示。

图6 目标侧倾角与侧向加速度关系曲线
在控制策略一中,EAAS 处于典型工作状态。首先将各传感器采集到的信号输入到电子控制单元输入模块,并将侧向加速度换算为车身侧倾角的目标值,然后采用Mamdani 模糊控制方法设计了EAAS模糊控制器,其次将左右高度传感器差值的绝对值转化为车身侧倾角,并以车身侧倾角与目标侧倾角的差值e及其变化率ec作为输入,最后以三相无刷电机驱动电路的上桥臂PWM 占空比d作为输出,此时下桥臂保持完全打开的状态,其控制系统原理如图7 所示。

图7 EAAS 模糊控制系统框图
设定e的模糊论域为[-5,5];ec的模糊论域为[-10,10]。由于通过PWM 占空比控制EAAS 内嵌的三相无刷电机的输出功率,故以PWM 占空比控制量d作为输出量的模糊论域为[-1,1]。对e和ec分别定义7 个模糊集合:NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大),对d亦定义7 个模糊集合:NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)。模糊控制输入、输出量的隶属函数均选用高斯型隶属函数。根据相关车辆专家经验、知识,确定模糊控制规则如表2 所示。
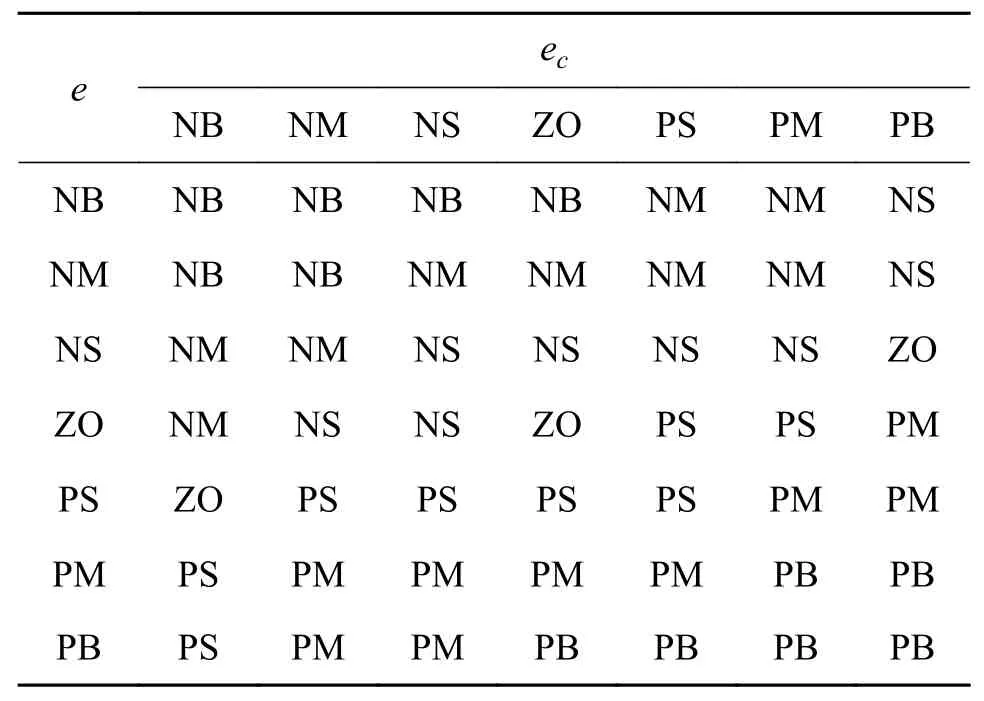
表2 模糊规则表
2.2.2 控制策略二
当车辆在水平路面上直线行驶时,此时左右车轮向同一方向等幅度跳动,EAAS 起不到抑制车身侧倾的作用。这种情况下,通过电子控制单元不生成驱动用6 路PWM 信号,电机处于自由转动状态,EAAS 左右两部分处于电解耦状态,有助于提升车辆平顺性。
2.2.3 控制策略三
当在不平道路上高速行驶时,若采取控制策略一的方式,EAAS 无法快速响应。因此,为有效提高车辆侧倾稳定性,将电机驱动电路的上桥臂全部关闭,对下桥臂实施PWM 控制方法,PWM 占空比由路面不平度确定,路面越不平,施加越大的PWM 占空比,反之则适当减小PWM 占空比。
2.2.4 控制策略四
当电子控制单元检测到系统发生故障时,此时为保证操纵稳定性,避免发生重大交通事故,采用控制策略四。该策略采取将电机驱动电路的上桥臂完全打开,下桥臂全部关闭,或者下桥臂完全打开,上桥臂全部关闭的方法,即系统处于“锁定”状态,其工作方式类似于传统被动式稳定杆。
本文主要对最关键的控制策略一开展研究,在角阶跃工况和鱼钩工况下进行离线仿真,最后利用半实物仿真试验验证其有效性。
3 离线仿真与半实物仿真试验
3.1 离线仿真试验
为验证上述整车动力学仿真模型、EAAS 模型及所提出的控制策略的有效性,分别选取前轮角阶跃输入工况、鱼钩工况分别进行仿真分析。本文所构建的整车动力学仿真模型直接以前转向轮转角作为输入,且设定左转时转角为正值,右转时转角为负值。对核心的控制策略一中3 种模式分别进行仿真。在考虑实际行车安全因素条件下,有效模拟出突遇障碍物时,驾驶员紧急操纵转向盘的避障行为,并使车身发生充分侧倾,本文设定试验车速为80 km/h,前轮转角幅值为10°。整车动力学仿真模型的部分参数如表3 所示。

表3 整车动力学仿真模型部分参数
1)前轮角阶跃工况的仿真参数设定:车速设定为80 km/h,路面等级设定具有路面附着系数为0.85 的B 级路面。前轮转角输入信号如图8 所示,图9 为车身侧倾角仿真结果。
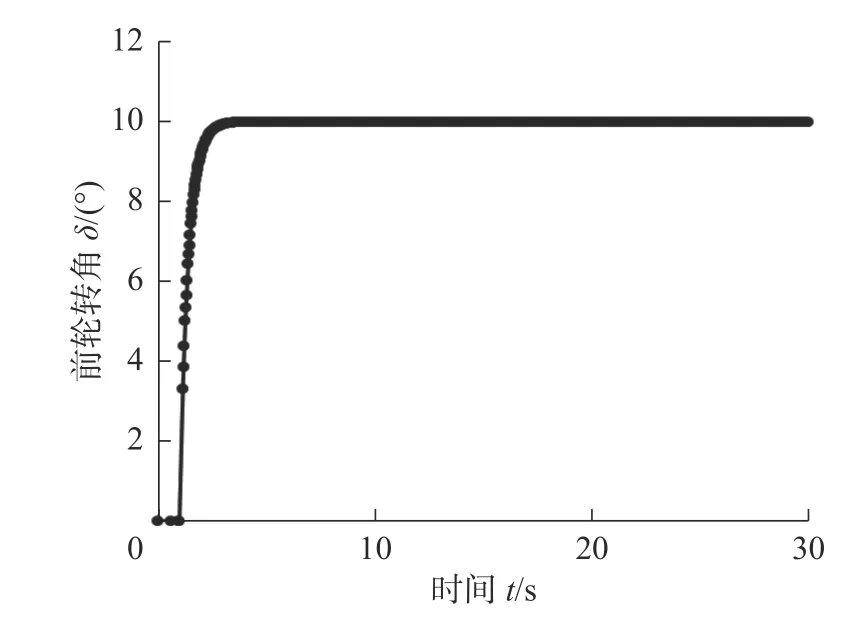
图8 前轮角阶跃输入工况前轮转角输入信号

图9 前轮角阶跃输入工况下车身侧倾角离线仿真结果
从图9 可得,在前轮角阶跃输入工况下,被动模式的侧倾角上升时间为4.54 s,侧倾角达到峰值的时间为7.24 s,最大超调量35%,稳态侧倾角值为2.0°。正常模式的侧倾角上升时间为4.62 s,达到峰值的时间为7.26 s,最大超调量55%,稳态侧倾角值为1.3°。柔顺模式的侧倾角上升时间为4.61 s,达到峰值时间为7.3 s,最大超调量46%,稳态侧倾角值为1.5°。运动模式的侧倾角上升时间为4.64 s,达到峰值时间为7.26 s,最大超调量51%,稳态侧倾角值为1.1°。相较于传统被动模式,本文提出的EAAS控制策略可更有效地控制车辆侧倾角,从而有效提升车辆侧倾稳定性,且3 种模式控制效果也满足控制需求,从而可以根据不同驾乘需求选择合适的工作模式。
2)鱼钩工况的仿真参数设定:车速设定为80 km/h,路面等级设定具有路面附着系数为0.85的B 级路面。前轮转角输入信号如图10 所示,图11为车身侧倾角仿真结果。

图10 鱼钩工况前轮转角输入信号

图11 鱼钩工况下车身侧倾角离线仿真结果
从图11 可得:在鱼钩工况下,被动模式正向侧倾角峰值为2.4°,反向侧倾角峰值为-3.5°,侧倾角稳态值为-2°;正常模式的正向侧倾角峰值为1.6°,反向侧倾角峰值为-2.7°,稳态侧倾角值为-1.3°;运动模式正向侧倾角峰值为1.4°,反向侧倾角峰值为-2.4°,稳态侧倾角值为-1.2°;柔顺模式正向侧倾角峰值为1.8°,反向侧倾角峰值为-2.9°,稳态侧倾角值为-1.5°。仿真结果表明鱼钩工况下所提出的新型控制策略仍然满足控制要求。
3.2 半实物仿真试验
为进一步验证具有多工作模式的EAAS 模糊控制策略有效性,并与离线仿真结果进行对比,开展了新型控制策略的半实物仿真试验,首先在上位机中利用MATLAB/Simulink 和Vehicle Network Toolbox构建如图12 所示的具有EAAS 的整车动力学仿真模型,然后设计搭建如图13 所示的EAAS 半实物仿真试验台架[1]。
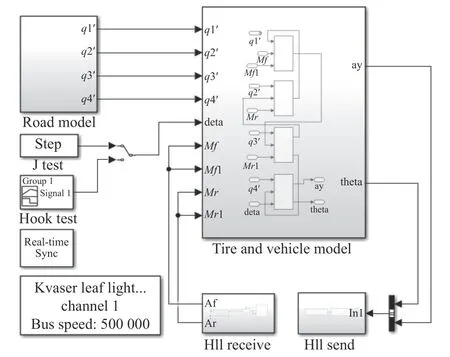
图12 EAAS 半实物仿真模型

图13 EAAS 半实物仿真试验台[1]
该半实物仿真台架主要工作原理如下:1)在上位机中设定前轮转角信号,以分别模拟角阶跃工况与鱼钩工况,Simulink/Desktop Real-Time 实时采集整车动力学仿真模型中的相关各车辆状态信号,并通过CAN 总线发送至EAAS 电控单元;2)该电控单元根据上述状态信号,令加载电控单元输出控制信号控制电动气泵工作,将高压空气充入储气筒;加载电控单元同时输出两路脉宽调制控制信号,分别控制组合电磁阀内两支比例电磁阀开度,实时调整左、右加载气缸输出的拉、压力值,以形成所需的车辆侧倾力矩;3)EAAS 电控单元同时根据车辆状态信号,利用相关算法得到当前状态下的期望反侧倾力矩,并实时控制EAAS 输出该反侧倾力矩,并通过CAN 总线将其反馈至整车仿真模型内。
EAAS 半实物仿真试验台架工作原理如图14所示,该台架主要部件参数如表4 和 表5 所示。

表4 拉压力传感器主要参数

表5 加载气缸主要参数
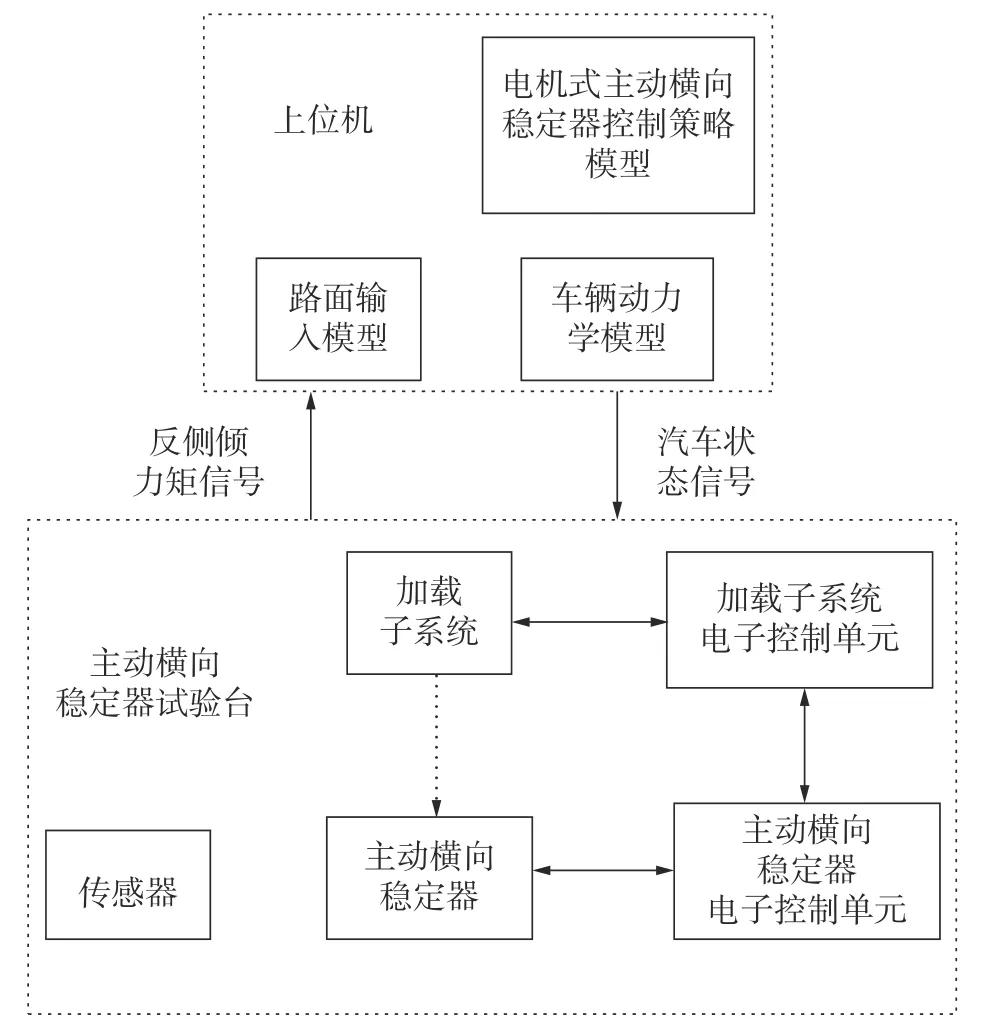
图14 半实物仿真试验工作原理图
在上位机中,分别建立具有EAAS 的整车动力学仿真模型及其模糊控制策略模型,并实现输入信号采集、数据实时处理、控制信号输出等功能。
利用英飞凌公司具有3 颗内核的TC275 微控制器设计了EAAS 电控单元,其主要由最小系统、电源子模块、驱动子模块、功率子模块、霍尔信号采集子模块、CAN 通信子模块等组成,如图15 所示。EAAS 试验台加载子系统电控单元亦采用TC275多核微控制器,其包括最小系统、电源子模块、电动气泵驱动子模块、组合阀控制子模块、CAN 通信子模块等,如图16 所示。

图15 EAAS 电子控制单元

图16 加载子系统电子控制单元
1)前轮角阶跃输入试验工况。前轮转角输入信号见图8,相关试验结果如图17 所示。
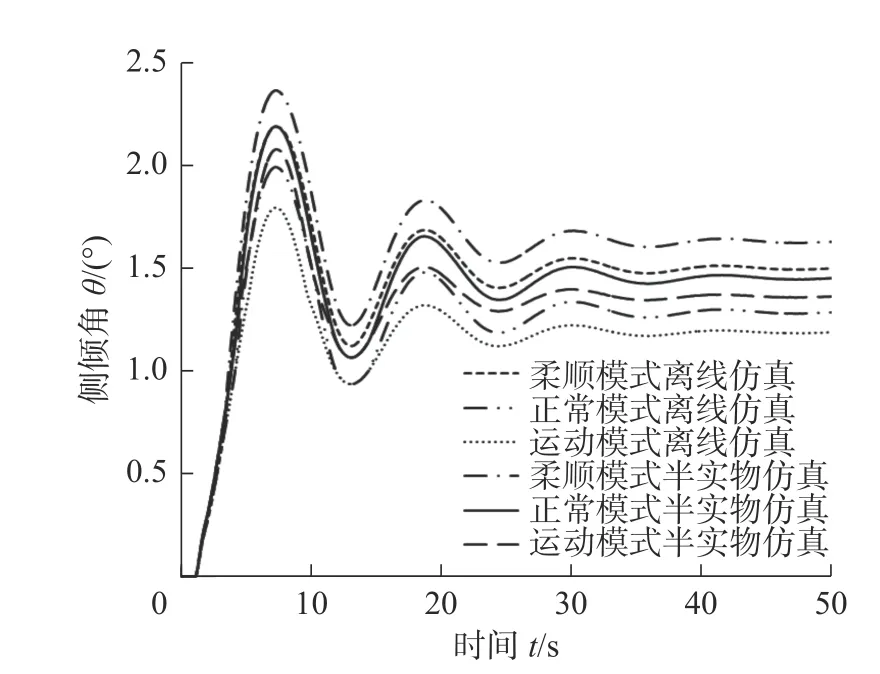
图17 角阶跃工况离线仿真与半实物仿真试验结果
由图17 可知,半实物仿真试验结果的稳态值比离线仿真结果大0.2°左右,总体结果接近,表明在半实物仿真试验条件下,本文所提出的控制策略仍然具有较好的有效性。
2)鱼钩试验工况。前轮转角输入信号见图10,相关试验结果如图18 所示。由图18 可知,在鱼钩工况下,半实物仿真试验结果的稳态值比离线仿真结果大0.15°左右,总体结果接近,进一步验证了提出的控制策略的有效性。
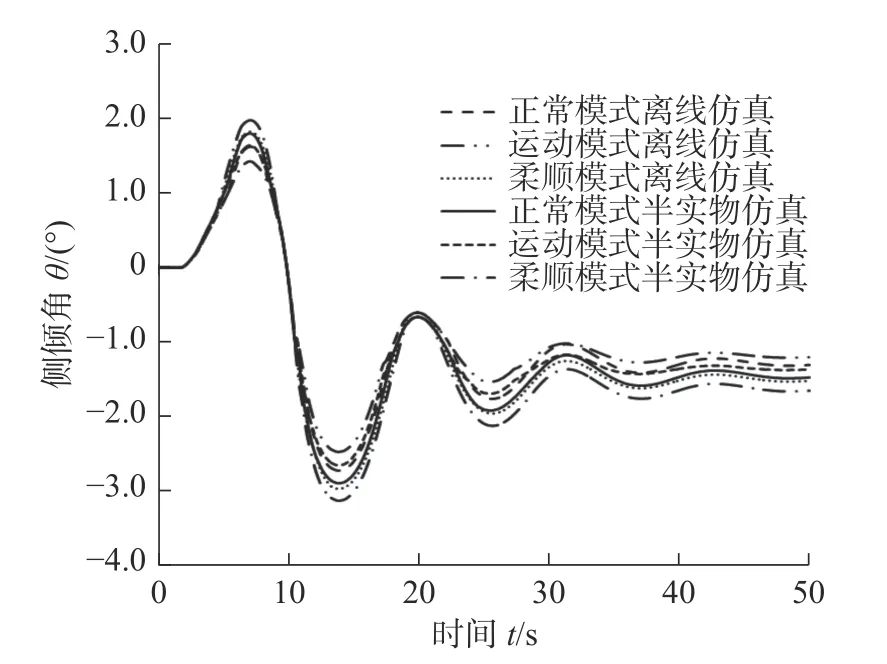
图18 鱼钩工况离线仿真与半实物仿真试验结果
4 结论
1)构建九自由度整车动力学仿真模型,在不同工况下对具有多工作模式的EAAS 控制策略进行离线仿真分析,仿真结果显示,前轮角阶跃工况下,相比于被动模式,正常模式、柔顺模式和运动模式车身侧倾角稳态值分别减小0.7°、0.5°和0.9°。鱼钩工况下,相比于被动模式,正常模式、柔顺模式和运动模式车身侧倾角稳态值分别减小0.7°、0.5°和0.8°。所提出的控制策略能够有效减小车身侧倾角,且能满足不同驾驶员的驾驶习惯。
2)搭建EAAS 控制策略的半实物试验平台进行半实物仿真试验,试验结果显示,前轮角阶跃工况下,半实物仿真试验结果的稳态值比离线仿真结果大0.2°左右,鱼钩工况下,半实物试验结果的稳态值比离线仿真结果大0.15°左右,试验数据较为接近,进一步验证了具有多工作模式的EAAS 模糊控制策略的有效性。

