旋转牵引式降落伞弹射系统动力学仿真与分析
阳碧慰,王敏
(1. 西南科技大学 制造科学与工程学院,四川绵阳 621010;2. 西南科技大学 工程技术中心,四川绵阳 621010)
随着民用无人机数量的不断增大,飞行安全问题日益凸显,无人机失控将对人类生命和财产带来严重的危害。无人机在飞行中的回收过程分为3 个阶段:无动力坠落阶段、降落伞弹射和充气阶段、自由飘落阶段。而当前无人机降落伞在低空降落成功率相对较低,主要原因是第二阶段用时太长,没有足够的减速缓冲高度。降落伞充气过程[1]包括初始充气、主充气和稳定下降这3 部分。由充气时间法[2]可知,初始充气阶段时间相对较长,是因为被压缩的降落伞的伞口张开面积几乎为零,使得空气无法快速进入降落伞。降落伞充气过程涉及伞衣结构与气动压力的相互作用,其流固耦合过程的求解作为降落伞研究领域的难点问题,一直备受研究者的关注,开伞性能难以准确预测[3]。
降落伞作为无人机常用的紧急降落工具,根据其弹射方式不同,可分为两类:一种以弹簧为动力弹射[4],该方式结构简单,控制方便,降落伞从压缩状态到充气完成需要的时间较长,对开伞高度要求高;另一种以压缩气体为动力弹射[5],具有响应快、伞口打开迅速、降落伞充气快等优点,但压缩气瓶制作成本高、工作震动剧烈、重复利用率低。本文基于开伞特性,将现有降落伞弹射方式加以整合优化,提出一种能高速旋转牵引开伞的无人机回收系统。通过对该系统进行理论设计和动力学仿真分析,验证了该方案的可行性,得出了该系统的工作特性,研究出了降落伞弹射过程中牵引球的运动规律。
1 系统结构组成
本文提出的旋转牵引式降落伞弹射系统主要适用于多旋翼无人机,以DJIS900无人机为例,该系统主要由降落伞、牵引球、滚筒仓体、推塞、弹簧、电机、舵机等组成,如图1 所示。

图1 降落伞弹射系统
由图1 可以看出,弹射系统安装在机身背部中心处,4 个呈圆周均布的牵引球分别连接降落伞伞口的十字对角。底部电机带动滚筒整体加速旋转,达到一定转速后,舵机通过连杆将滚筒内的推塞解锁,其底部的压缩弹簧被释放并顶开仓盖,将降落伞高速推送出仓。牵引球出仓后具有向上的速度和旋转切向速度,当速度合成后,牵引球做斜抛运动向四周发散[6],并将动能转化为打开伞口所需的能量。伞口在出仓后被迅速拉开,气流快速充入降落伞,使降落伞发挥减速作用。
降落伞弹射机构的触发条件有手动触发和自动触发两种。图2 为降落伞弹射机构的自动触发流程。可以看出,当陀螺仪传感器检测到飞行姿态异常时,或者控制系统检测到无人机线路异常时,又或者遥控信号接收异常时,均可自动触发该降落伞弹射机构。T-11 型伞兵伞的几大特点[7]均与无人机的设计要求相符合,其结构在无人机回收伞的设计上具有较好的应用前景。因此,伞衣采取了类似于T-11 高级战术伞降系统(Advanced tactical parachute system,ATPS)的十字形结构,如图3 所示,它具有开伞高度低、稳定性高、摆动角小等优点。
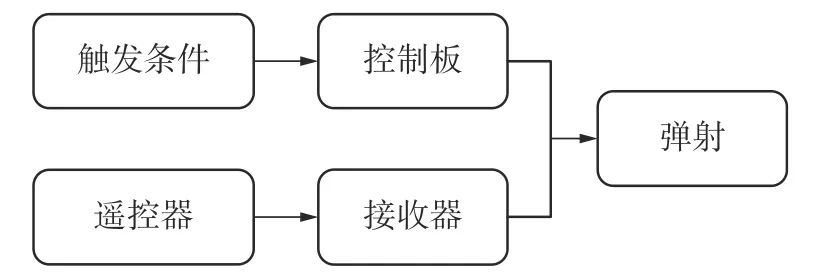
图2 降落伞弹射系统的自动触发流程

图3 T-11 高级战术伞降系统
2 动力学模型建立
2.1 系统模型
降落伞的充气过程是一个非常复杂的非稳定过程,是全世界公认的空气动力学领域的一个难题[8]。为了方便在Adams 中模拟牵引球在降落伞弹射过程中的运动规律,在不影响主要运动的基础上,做出以下假设:
1)由于空气阻力与降落伞阻尼受干扰因素大,且具有不确定性,但可通过增大功率的方法降低其带来的影响,所以假设空气阻力与降落伞阻尼为0;
2)由于降落伞在弹射出仓过程中体积变化较小,所以弹射过程用等质量、等体积的圆柱体近似代替降落伞;
3)为了方便观察牵引球的运动轨迹,基于前两项假设,将装置固定在地面进行静态弹射。
由于牵引球在竖直方向上受到重力作用,做初速度为Vy、加速为g的匀减速运动,速度与水平方向夹角为θ,故系统速度方程如下:
在x、y方向上,关于时间t的速度和位移函数为:
小球到达最高点,所用的时间为
抛物运动轨迹方程式为
射高为
伞直径的确定为:
式中:g= 9.81 N/kg;ρ为空气密度,ρ= 1.22 kg/m3;Cd为十字形伞阻力系数,Cd≈ 3.53。机身负载时约重5 kg,通过计算得到降落伞直径D= 1.346 7 m。
2.2 参数设置
在Adams 中设置各零件之间的运动副,具体设置如表1 所示。由于舱盖通过摩擦力实现仓口封闭,在弹射过程中参与作用较小,可忽略不计。在初始状态,4 个钢球在推塞挡片内,推塞上方留出降落伞存放空间,自然长度为120 mm 的弹簧作为弹射蓄能。压力函数设置为0 + step(time,1,8,1.000 1,0),表示以8 N 的压力作用于推塞,在1 ~ 1.000 1 s 时间段,压力从8 N 减小到0 N,模拟弹簧释放。通过无刷电机驱动整个仓体旋转,在仿真环境中,添加MOTION 驱动实现模拟,其余参数如表2 所示。
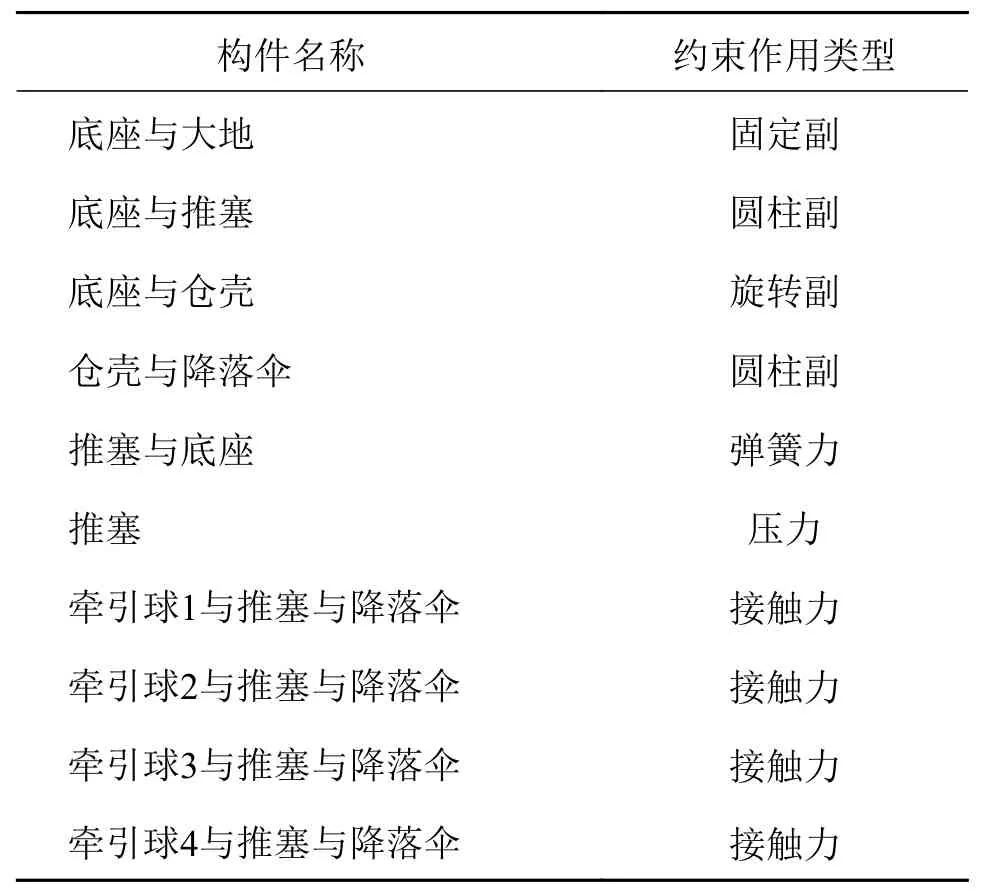
表1 零件之间的运动副设置

表2 其余参数设置
仿真时长为2 s,步数为2 400,完成的动力学仿真模型如图4 所示。

图4 动力学仿真模型
3 仿真结果与分析
通过在Adams 进行动力学仿真,得出牵引球运动轨迹前视图如图5 所示。可以看出,仓体在1 s内角速度从0 加速到2 000 °/s,压缩弹簧释放,推塞将牵引球和降落伞推出,降落伞出仓后旋转上升,牵引球出仓后具有竖直方向和水平方向的初速度,分别做斜抛运动,向四周散开,其俯视图见图6。通过多次仿真测试,得到最佳开伞条件为:电机转速2 000 °/s,弹簧刚度系数80 N/m。当牵引球运动到最高点时,恰好与降落伞完全打开时的伞口边缘A点近似重合,如图7 所示。

图5 牵引球运动轨迹前视图

图6 牵引球运动轨迹俯视图

图7 牵引球与伞口的位置关系
以牵引球2 为例(下同),将其仿真数据在软件Origin 中绘制图形,如图8 所示。可以看出,牵引球出仓后的运动轨迹近似于在三维空间中的一条抛物线,刚开始的旋转曲线表示牵引球在仓内的运动轨迹。

图8 牵引球的运动轨迹
3.1 牵引球速度变化特征
牵引球竖直方向速度Vz随时间的变化如图9所示。可以看出,曲线初始有波动,是由于模型中推塞的初始位置略高于弹簧压缩平衡时的位置导致的。仿真开始后,因重力作用形成的波动在约0.5 s后趋于平衡,不会影响后续弹射。在1 s 时,压缩弹簧释放,弹射开始,整个过程持续0.029 8 s,速度Vz从0 增加到3.734 m/s;在1.029 8 s 时,牵引球出仓做斜抛运动,竖直方向仅受重力作用;1.403 3 s时,Vz为0,牵引球到达竖直方向上的最高点。

图9 牵引球在z 轴方向的速度
牵引球在x和y方向的速度分别如图10 和图11 所示。可以看出,在1 s 内的加速阶段,Vx和Vy逐渐增加,而牵引球出仓后速度恒定,这说明无阻力情况下,牵引球稳定性较好。若考虑空气阻力和降落伞阻尼,曲线从1.029 8 s 后,速度会逐渐减小。
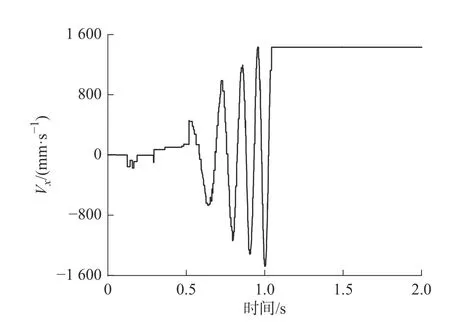
图10 牵引球在x 轴方向的速度

图11 牵引球在y 轴方向的速度
牵引球从仓口抛出的初速度V0为
V0与水平方向的夹角θ为
由此可知,牵引球在出仓时刻速度达到最大值,出仓后其速度线性减小。
3.2 牵引球位移变化特征
牵引球在z轴方向的位移如图12 所示。可以看出,在1 s 时,弹射开始;1.029 8 s 出仓时刻在图中不易观察;在1.403 3 s 时,牵引球到达竖直方向最高点,之后便开始下降。牵引球运动到最高点时,降落伞伞口刚好完全打开,可以保证伞与机身有足够的距离。
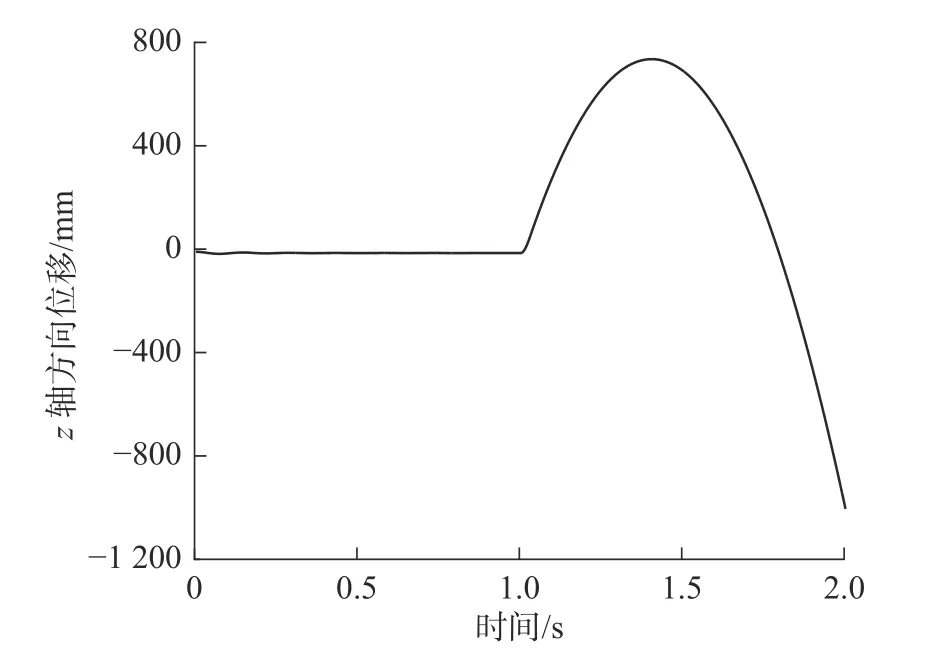
图12 牵引球在z 轴方向的位移
牵引球在x轴与y轴方向的位移分别如图13和图14 所示。可以看出,在1.029 8 s 时,牵引球做匀速运动,其在xoy平面内的和位移直接反应牵引伞口张开大小随时间的变化情况;在1 s 时,曲线越陡表示Vx与Vy的和速度越大,伞口张开速率越快。而和速度是由电机转速决定的,当电机转速为2 000 °/s 时,最高点的水平位移为677.938 7 mm,该值近似于降落伞的计算半径。因此,在仿真环境下,电机转速取2 000 °/s 为最优值。
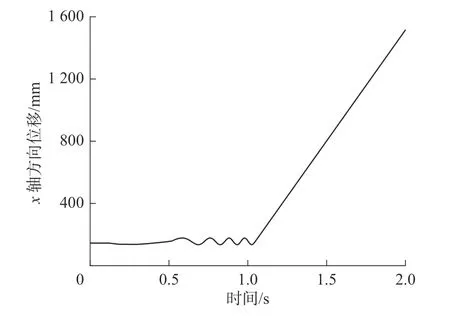
图13 牵引球在x 轴方向的位移
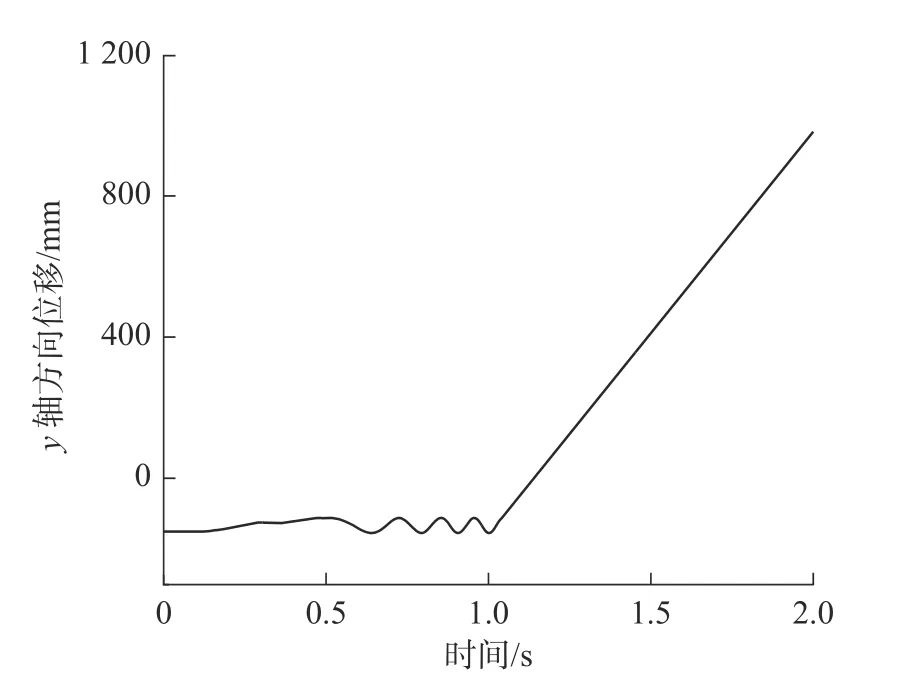
图14 牵引球在y 轴方向的位移
3.3 牵引球能量转化特征
牵引球的动能和重力势能分别如图15 和图16所示。可以看出,在1.029 8 s 时,牵引球的动能达到最大,之后由于重力影响,动能转化为重力势能;在1.403 3 s 时,牵引球的势能达到最大。出仓后牵引球的动能处于衰减状态,是因为仿真条件中简化的模型伞与牵引球没有连接,牵引球运动到1.403 3 s即为仿真完成,之后时间段为无效值。若考虑空气阻力和降落伞阻尼,则动能将转化为重力势能和克服阻力做功[9],那么实际情况将需要更大的初始能量,这可分别通过改变电机转速和弹簧刚性系数来调整弹射功率。不同类型降落伞的名义直径和开伞用时如表3所示。可以看出,与现有几款无人机回收伞降系统[10-12]相比,旋转牵引式降落伞弹射系统的开伞用时仅为1.403 3 s,比以往系统快0.5 s 以上。

表3 不同类型降落伞的名义直径和开伞用时

图15 牵引球的动能
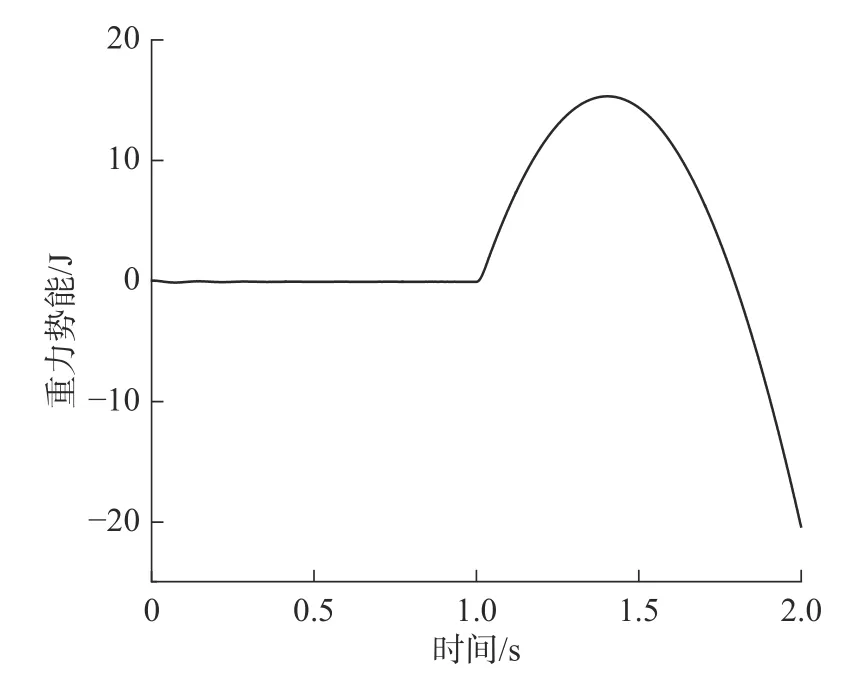
图16 牵引球的重力势能
3.4 优化验证
综上所述,通过动力学仿真结果分析,增大电机转速可以增大牵引球在水平方向的速度和位移,增大弹簧刚性系数可以增大牵引球在竖直方向上的速度和位移。改变参数后,牵引球出仓方向将不同,为了方便观测牵引球的运动轨迹,建立Sz-o-Se平面,将牵引球的三维轨迹投影到二维平面内,对多组数据进行观察和比较[13]。弹簧刚度系数保持80 N/m,以理想电机转速2 000 °/s 为参考,通过增减电机转速值,测得牵引球的运动轨迹如图17 所示。考虑到实物实验中还需要增加电机转速克服空气阻力和降落伞阻尼,所以取3 组梯度较大且大于理想电机转速的转速值。可以看出,随着电机转速的增大,牵引球在水平方向的位移逐渐增大[14-15]。

图17 不同电机转速下牵引球的运动轨迹
电机转速保持2 000 °/s,以理想弹簧刚度系数80 N/m 为参考,通过增减弹簧刚度系数,测得牵引球的运动轨迹如图18 所示。同样,考虑到实物实验中,还需要通过增大弹簧刚度系数克服空气阻力和降落伞阻尼,所以取2 组大于理想弹簧刚度系数的数据。可以看出,随着弹簧刚度系数的增大,牵引球在竖直方向的位移逐渐增大。
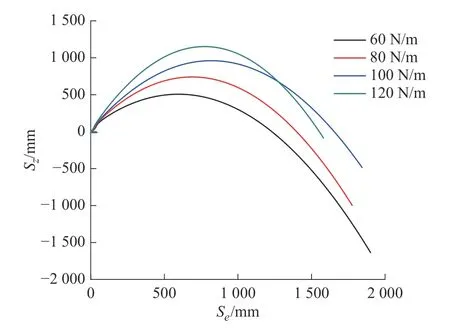
图18 不同弹簧刚度系数下牵引球的运动轨迹
牵引球的质量也是影响其运动轨迹的因素之一,根据动能计算式,即
可知,相同初速度的条件下,质量越大,动能越大。因此,可通过适当增加牵引球的质量来增大其动能。但在有阻力状态下,质量增加会导致牵引球射程降低[16],而且容易出现旋转摆动剧烈及旋转启动慢的现象。关于质量因素本文未做详细研究,后续将继续展开分析。
4 结论
1)通过多次仿真测试,得到最佳开伞条件为:电机转速2 000 °/s,弹簧刚度系数80 N/m。当牵引球运动到最高点时,恰好与降落伞完全打开时的伞口边缘近似重合。
2)牵引球出仓时,动能最大,随后逐渐减小,转化为重力势能。牵引球出仓后,水平方向上速度恒定,位移匀速增加;竖直方向上速度线性降为0,位移先增大后减小。
3)与以往系统相比,旋转牵引开伞时间仅为1.403 3 s,开伞用时至少缩短了0.5 s。
4)当弹簧刚度系数恒定时,牵引球水平方向的位移随电机转速的增大而增大;当电机转速恒定时,牵引球竖直方向的位移随弹簧刚度系数的增大而增大。

