地铁车辆蜂窝式防爬器的结构设计及优化
陈佳明,朱涛,肖守讷,阳光武,杨冰
(西南交通大学 牵引动力国家重点实验室,成都 610000)
随着高速轨道列车的蓬勃发展,国内外轨道车辆碰撞事故时有发生[1]。嵌入吸能结构是提高车辆耐撞性能和降低事故损失的有效技术手段。防爬器是防止相撞车辆发生攀爬、脱轨等极端不利后果的重要安全装置,同时也是车端吸能结构的重要组成部分,通常由防爬齿、吸能模块、中部导向梁、安装基盘等组成。按照其吸能区构造的不同一般分为切削式、蜂窝式和胀管式等[2],蜂窝式防爬器由于其轻量化、比吸能高、变形可控等优点,近年来越来越受到学者们的重视。
现阶段,学者们对于防爬器的研发主要着眼于对其结构优化设计,提高其吸能特性或满足其轻质要求。马艳波[3]结合结构刚度、强度和设计工艺等要求,对防爬齿进行了精细化设计, 优化设计的防爬齿的质量较常规设计减轻了10.24%。梁炬星[4]设计了一种切削厚度随切削行程渐变、切削行程可控的新型切削式防爬器,实现了在碰撞过程中界面力在一定范围内可控。岳伟玲等[5]提出一种新型的拉削式防爬器,并根据轨道车辆吸能器的吸能要求对其进行了初步的结构设计。Peng 等[6]通过试验和仿真相结合的手段,分析了切削深度、切削角和切削圆心角等设计参数对切割式吸能装置的冲击性能的影响。因为防爬器在碰撞过程中其吸能特性指标与结构参数呈高度非线性的关系,并不能使用一般方程来表达,故使用代理模型进行结构耐撞性优化设计是其常用的手段[7]。陈淑琴等[8]采用响应面法研究了防爬齿齿高和倾角对防爬器防爬能力的影响因素。Du 等[9]用Kriging 模型描述了火箭发动机结构参数与其模态频率之间的关系,对其进行优化,提高了发动机结构的振动频率。申爱民和贺严松[10]设计径向基函数(RBF)神经网络控制器,对车辆非线性液压悬架进行了优化,提高了其行驶稳定性。
综上,目前学者们对于多级串联式的蜂窝式防爬器的研究较少,如何诱导蜂窝式防爬器在压溃过程中稳定变形,从而达到最佳的吸能效果,是蜂窝式防爬器研发工作的重点。本文根据轨道车辆耐撞性标准,对轨道车辆用蜂窝式防爬器吸能区域的结构进行合理设计,建立了多级串联型蜂窝式防爬器的有限元模型并进行仿真分析。为了使其在碰撞吸能过程中发挥更好的吸能效果,以压缩力效率为优化目标,通过使用四次多项式响应面法和多岛遗传算法在设计空间中寻找到其最优的壁厚组合,对其进行优化设计,从而为蜂窝式防爬器在轨道交通行业的应用提供了参考。
1 蜂窝式防爬器结构设计
本文所设计的蜂窝式防爬器由前端防爬齿、矩形渐变薄壁壳、正六边形铝蜂窝、蜂窝隔板、工字钢引导装置等组成,其结构示意图见图1。较传统的单级蜂窝式防爬器不同的是,该防爬器采用多级蜂窝串联结构,不同蜂窝之间采用隔板隔开,在蜂窝压溃变形时更加有序可控。将薄壁壳设计成渐变形式是因为渐变矩形截面的薄壁结构在比吸能上优于直截面矩形薄壁结构[11]。

图1 蜂窝式防爬器结构示意图
根据国内某型地铁所要求的蜂窝式防爬器性能参数要求和欧洲铁路标准EN15227-2008[12]对于轨道车辆25 km/h 发生碰撞时对于防爬器的规定,本文所研究的蜂窝式防爬器技术参数要求如表1所示。
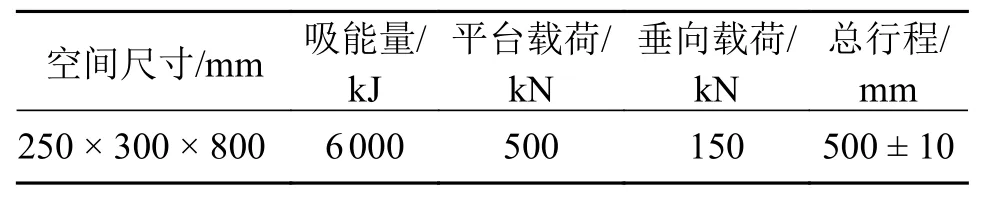
表1 蜂窝式防爬器参数要求
根据以上规格要求,可从蜂窝式防爬器的垂向、纵向载荷承载能力以及吸能性能3 个方面来评判其性能是否达标。其中,垂向载荷承载能力越弱,爬车风险越大,一旦发生爬车事故,连挂车辆相继发生脱轨的概率就大大增加,将严重威胁司乘人员的安全。纵向载荷承载能力关系着防爬器在碰撞过程中的吸能能力,其纵向可承载的载荷越大,防爬器的抗冲击性能越强,吸收完所有能量所压缩的行程越短。
1.1 蜂窝式防爬器垂向承载能力设计
该蜂窝式防爬器在碰撞中的受到来自防爬齿上的垂向载荷后,主要由薄壁壳和工字钢来承担,其垂向承载能力的大小,取决于所选用的材料和所设计的形状。由于安装座是固定于车体上的,可将承受垂向载荷的薄壁壳和工字钢构件简化为悬臂梁模型。通过对这两种结构垂向弯曲应力的计算,来粗略估计出该防爬器的垂向承载能力。该蜂窝式防爬器的正面和侧面的截面示意图如图2所示。

图2 蜂窝式防爬器截面示意图
薄壁壳在防爬器高度方向上长度不变,而宽度渐变,前窄后宽。宽度取高度方向的平均值,将薄壁壳的截面简化为一个空心矩形,其垂向截面系数为
对于工字钢结构,其垂向截面系数为
防爬器所能承受的最大垂向弯矩应满足的条件为
式中:Fz为防爬器所承受的垂向载荷;x为防爬器的长度;W总为防爬器总的垂向截面系数,W总=Wx1+Wx2; [σ]为材料的许用弯曲应力。代入数据计算出最大垂向载荷Fz应满足的条件为
该蜂窝式防爬器可承受的最大垂向载荷为388.7 kN,大于150 kN,满足标准规定。
1.2 蜂窝式防爬器纵向承载能力设计
在两列车碰撞过程中,两车蜂窝式防爬器的防爬齿相互啮合,阻止车辆发生攀爬;同时工字钢随防爬齿后退穿过隔板,铝蜂窝吸能块和薄壁壳受压变形,吸收撞击能量。两者承载纵向载荷的作用是相互耦合、非线性的,并不能通过理论计算得到。故分别计算并叠加两者的纵向承载力,来粗略估计出该防爬器的纵向承载能力。
对于矩形薄壁壳结构,其进入稳态压溃阶段的平均载荷值[13]为
式中: σ0为材料的屈服强度,MPa;t为壁厚,mm;v0为碰撞初速度,mm/s;p、q为材料常数。取壁厚t=3 mm,v0=6.944 m/s,根据文献[14],取p=5,q=40。计算可得矩形渐变薄壁壳承载的理论平台纵向载荷为197.8 kN。
技术参数要求的防爬器所能承受的纵向平台载荷为500 kN,除去上述计算的薄壁壳承载的纵向载荷,剩余蜂窝应承受的纵向载荷为302.2 kN。用有限元软件建立单个蜂窝块的模型,其胞元边长为7 mm,壁厚为0.3 mm,用一面刚性墙以25 km/s 的速度对其进行压溃。得到单个蜂窝块的稳定压溃阶段应力-应变曲线如图3 所示。

图3 单个蜂窝块应力-应变曲线
由图3 中数据计算得到其稳态压溃阶段平台应力为14.05 MPa,根据技术参数要求,蜂窝所至少需要具有的截面面积为
故将蜂窝块设计为两排,并排分布于工字钢引导装置的两侧,每排5 个蜂窝块。前后每两块蜂窝夹一块隔板,一共4 块隔板。每个蜂窝块的尺寸为85 ×150 × 98.5,则两排蜂窝的截面面积一共为25 500 mm2,蜂窝所承受的纵向载荷大于302.2 kN,满足其技术要求。
1.3 蜂窝式防爬器的有限元模型
由于蜂窝的尺寸过长会造成吸能过程中的失稳变形,故需将其设计为尺寸合适的蜂窝块进行并联起来,中间与隔板相连。在碰撞吸能过程中,隔板在工字钢引导装置上滑动可以起到缓冲和引导蜂窝纵向有序变形的作用。
铝蜂窝采用精细化建模,正六边形蜂窝胞元的边长为7 mm,隔板厚度为3 mm。隔板中开供工字钢引导装置穿过的引导槽。该防爬器通过安装座与车体底架连接。
因该蜂窝式防爬器在头车前端对称布置了两个,故在仿真过程中,在安装座上添加mass 单元,将其配重为16.05×103kg,即头车质量的一半。根据文献[8]的研究方法,两辆地铁车辆以25 km/h 速度对撞时的吸能量可以换算为一辆地铁头车以15 km/h 碰撞刚性墙的吸能量。故给防爬器施加4.167 m/s(即15 km/h)的速度撞击刚性墙,从而模拟安装该防爬器的单节头车发生碰撞的过程。模型中薄壁壳、工字钢引导装置、隔板和防爬齿采用Q355 钢,铝蜂窝采用24 号材料模型(MAT_PIECEWISE_ LINEAR_PLASTICITY),其密度为2 700 kg/m3,正六边形蜂窝的精细化建模如图4 所示。

图4 防爬器内部蜂窝有限元模型
2 蜂窝式防爬器有限元仿真结果
2.1 3 种类型防爬器的对比
比吸能SEA(Specific energy absorption)是评价吸能装置的重要指标之一,它包括质量和体积比吸能,对比不同吸能装置的质量比吸能一般是用准静态工况压缩相同长度的吸能装置,进而用各自的吸能量除以各自该段长度的质量得出。比吸能ESEA表达式为
式中:F(x) 为 吸能装置纵向的碰撞力;ml为该段压缩长度的质量,l为压缩长度。
为探究多级蜂窝式防爬器在比吸能等方面的特有优势,建立与该蜂窝式吸能防爬器质量相同的普通圆管压溃式的防爬器的有限元模型,如图5 所示。此外,在多级蜂窝式防爬器的有限元模型中去掉隔板,将剩下的各个蜂窝块直接相连,建立没有隔板的单级蜂窝式防爬器有限元模型,以对比它和单级蜂窝式吸能效果的差异。

图5 圆管式防爬器有限元模型
因比吸能是在结构压溃部分质量相同的条件下对其吸能量的对比,故将三者固定,分别用移动的刚性墙以0.1 m/s 的准静态速度压缩100 mm,对比该工况下两者的吸能量、比吸能以及压缩力效率大小。其位移-撞击力的对比如图6 所示。各吸能参数的对比如表2 所示。
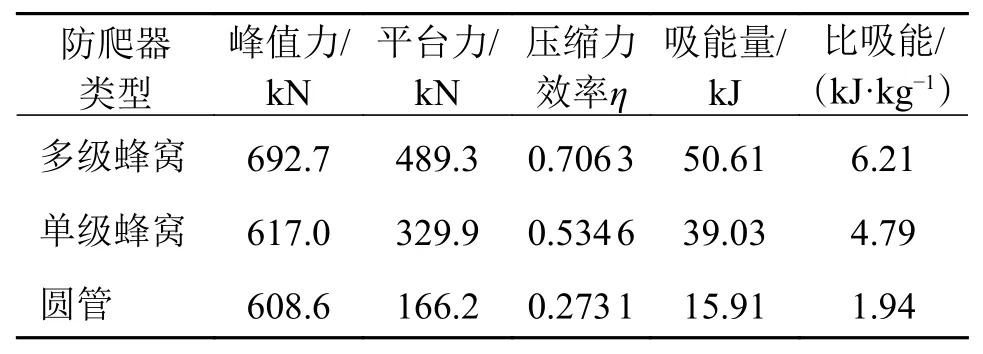
表2 防爬器吸能特性对比

图6 防爬器撞击力对比
由表2 可知,圆管式防爬器的峰值力较大而平台力较小,蜂窝式防爬器的峰值力略大于圆管式而平台力远大于圆管式。因此多级蜂窝式防爬器的压缩力效率比圆管式的高出了61.33%,单级蜂窝式防爬器的压缩力效率比圆管式的高出了48.92%。压缩相同长度的蜂窝式和圆管式防爬器,在三者的压溃部分质量都为8.15 kg 的情况下,多级蜂窝式防爬器吸能量为50.61 kJ,单级蜂窝式防爬器为39.03 kJ,圆管式为15.91 kJ,比吸能多级比单级高出了22.87%,多级比圆管式高出了68.76%。故多级蜂窝式防爬器在压缩力效率和比吸能方面具有明显优势,既能实现轻量化,降低地铁车辆行驶中的能耗,又能在发生碰撞的情形下,在其行程内吸收完巨大的碰撞能量,保证司乘人员的安全。
2.2 蜂窝式防爬器的仿真结果
因在防爬器的碰撞过程中,主要是由吸能区的铝蜂窝和渐变薄壁壳对吸能产生贡献。两者厚度相适应,才能发挥较佳吸能效果。故在该优化问题中,选取蜂窝的壁厚t和薄壁壳的壁厚a为设计变量,对该蜂窝式防爬器结构进行优化。为了充分探究两种壁厚对蜂窝式防爬器吸能的影响,选取a、t的取值范围为2.2 mm≤a≤3 mm、0.26 mm≤t≤0.34 mm,采用2 因素5 水平的全试验设计方法在该范围内为a、t进行取值,一共有25 种不同的壁厚组合,并用3.1 小节设计的工况进行有限元计算。
图7为不同壁厚组合下蜂窝式防爬器的撞击力-位移曲线,随着蜂窝壁厚t的增加,或是随着薄壁壳的壁厚a的增加,该蜂窝式防爬器在碰撞过程中的整体撞击力和峰值撞击力都随之增大。由于增加两种壁厚均使得防爬器的承载能力增加,防爬器会在更短的行程内吸收完碰撞产生的全部能量,因此最大压缩位移减小。相较铝蜂窝壁厚,薄壁壳厚度的改变对撞击力的影响更为显著,增大其厚度撞击力波动更为剧烈。
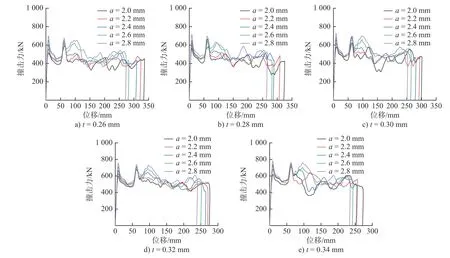
图7 蜂窝式和圆管式防爬器撞击力对比
由图8 的变形情况可得,该多级蜂窝式防爬器由于在碰撞过程中其内置铝蜂窝是和外层薄壁壳一起参与压溃变形,卡在薄壁壳上的隔板会随薄壁壳的变形而发生弯曲变形,导致蜂窝的压缩并不稳定。故撞击力的波动也较典型蜂窝的力-位移曲线更大。最终,一共有4 排蜂窝块参与了吸能,吸收完该碰撞工况下的全部能量。不同壁厚组合下的防爬器的位移-撞击力曲线在压溃位移为100 mm 内的波动较为剧烈,由于薄壁壳上设置了诱导槽,在该位移段内出现了两次较为明显的峰值撞击力;在100 ~300 mm 位移段内位移-撞击力曲线的波动较为平缓。将较为平缓的这段曲线数据取均值,得到不同壁厚组合下的平台撞击力。

图8 蜂窝式防爬器的内部变形情况
3 压缩力效率η 优化研究
在地铁车辆发生的碰撞事故中,过大的碰撞初始峰值力不仅会对车体结构造成巨大破坏,也严重威胁着车内乘客的安全。蜂窝稳定压溃的平台力阶段是吸能的主要阶段,在平台力不超出安全阙值的情况下,平台力越大则蜂窝的吸能性能越好。故本文采用评价吸能性能的指标之一:压缩力效率η(Compression force efficiency),其表达式为
式中FM为碰撞的最大峰值力。
3.1 压缩力效率η 优化模型及验证
在对该蜂窝式防爬器进行结构设计过程中,当FM较小,Fm较 大时,则计算得到的压缩力效率 η值较大,说明结构不仅吸能效果较好,而且降低了碰撞造成的损伤。故将压缩力效率η 作为优目标函数,并添加该优化问题的约束条件,其数学表达式为:
响应面模型是利用多项式函数拟合设计空间,能够通过较少的输入参数在局部范围内比较准确地逼近实际的函数关系。文献[15]中通过对比,发现四次多项式响应面代理模型精确度高于二次多项式,故本文采用该模型来模拟目标函数与变量之间复杂的非线性关系。
在变量的约束条件限制空间内,目标响值y与设计变量x之间的映射关系式[15]可以表示为
其中,样本点x的集合为{x1,x2,···,xi}(i=1,2,···,n),将响应函数展开得
将仿真所得的25 组数据用四次多项式函数拟合得到以压缩力效率 η为响应值,蜂窝壁厚t和薄壁壳壁厚a为设计变量的多元回归模型,可表示为
四次多项式函数代理模型的压缩力效率 η响应面如图9 所示。从该响应面图可以看出,压缩力效率与蜂窝壁厚和薄壁壳壁厚之间并没有单调递增或递减的关系,且很难从图中直接观测出压缩力效率的最大值,故在下一节将利用遗传算法在该约束条件下寻找其最优值。

图9 压缩力效率η 响应面
利用响应面代理模型的误差平方和均方根RMSE 的值对其进行验证。RMSE 表示响应计算值和仿真结果之间的相似度,反映了该代理模型的精确程度。RMSE 的值越小,则相应代理模型的精度较高。其计算公式为
式中:y(x)为目标响应值;y(x)为代理模型得到的预测值。
为了检验四次多项式响应面代理模型的精度,在设计空间内继续选取除了之前25 组输入样本数据外的8 个样本点,分别计算其有限元得到的目标响应值和代理模型预测值,代入式(11)计算得R2,选取样本点和计算结果如表3 所示。

表3 样本点的选取及其计算结果
经过计算,该组数据的误差平方和均方根RMSE 的值为0.028 0,其值较小,说明该四次多项式响应面代理模型的有较高的精度,其预测的结果是可靠的。
3.2 多岛遗传算法寻优分析
多岛遗传算法是对并行分布遗传算法的改进,适用于单变量函数的全局优化设计,具有比传统遗传算法更优良的全局求解能力和计算效率。多岛遗传算法的周期性迁移操作保持了优化解的多样性,提高了优化速度,在一定程度上可以解决传统遗传算法过早收敛,易陷入局部最优的问题[16]。设置多岛遗传算法的参数如表4 所示。通过多岛遗传算法得到的四次多项式响应面代理模型关于压缩力效率的最优值如表5 所示。

表4 多岛遗传算法的参数

表5 多岛遗传算法优化结果
寻优发现在蜂窝壁厚t为0.31 mm,薄壁壳壁厚a为2 mm 的条件下,蜂窝式防爬器的压缩力效率取得最大值。代理模型与有限元计算误差仅为0.60%,说明了该四次多项式响应面模型的寻优结果是可靠的。优化前的峰值力为712.49 kN,优化后降低了1.87%,优化前的平台力为468.40 kN,优化后提高了4.22%,压缩力效率优化后提高了6.03%,达到了对其吸能能力优化的目的。可见优化后该蜂窝式防爬器在吸能过程中载荷具有更好的平稳性,既降低了较大峰值力对于结构的损伤和乘员安全的侵害,又提高了平台力,使其在有效行程内能吸收完巨大的碰撞能量。总之,利用多岛遗传算法达到了对蜂窝式防爬器吸能能力优化的目的,该结果对其在工程中的应用提供了有益的参考。
4 结论
1)对比相同质量的多级、单级蜂窝式防爬器和圆管式防爬器,在准静态压缩相同长度的条件下多级蜂窝式防爬器的吸能量最多。对比三者的比吸能和压缩力效率,多级蜂窝式防爬器比单级的高出20%以上,比圆管式的高出60%以上。说明多级蜂窝式防爬器具有载荷平稳,抗冲击性能强,能吸收较大能量的特性。
2)薄壁壳壁厚对多级蜂窝式防爬器的撞击力影响较铝蜂窝壁厚更为显著,随着薄壁壳厚度的增加,防爬器压溃位移减少,撞击力波动更为剧烈。诱导槽在引导防爬器变形的同时会使二次峰值力更加明显。
3)运用四次多项式响应面代理模型对蜂窝式防爬器的压缩力效率进行拟合,并选取样本外的点,计算其误差平方和均方根RMSE,证明了该代理模型具有较高的精度。因此在一定精度范围内该模型可替代相应的数值模型,从而能减少有限元的计算量,在优化设计问题中有效缩短设计周期。
4)利用多岛遗传算法对蜂窝式防爬器的压缩力效率的最大值进行寻优,发现当薄壁壳壁厚较小,蜂窝壁厚适中时其压缩力效率较高。优化后蜂窝式防爬器的峰值力有所降低,平台力有所提高,压缩力效率比优化前提高了6.03%,相较圆管式防爬器提高了60.96%,取得了较好的优化效果。

