采样点分布对基于面形斜率径向基模型的自由曲面拟合精度的影响
武鹏飞,张 赞,郑 义,张 娟,王尧尧,赵 星*,王灵杰,伍雁雄
(1.南开大学 现代光学研究所 光学信息技术科学教育部重点实验室,天津 300071;2.中国科学院 长春光学精密机械与物理研究所光学系统先进制造技术中国科学院重点实验室, 吉林 长春 130033)
采样点分布对基于面形斜率径向基模型的自由曲面拟合精度的影响
武鹏飞1,张赞1,郑义1,张娟1,王尧尧1,赵星1*,王灵杰2,伍雁雄2
(1.南开大学 现代光学研究所 光学信息技术科学教育部重点实验室,天津 300071;2.中国科学院 长春光学精密机械与物理研究所光学系统先进制造技术中国科学院重点实验室, 吉林 长春 130033)
鉴于自由曲面模型的面形拟合精度在自由曲面表征以及面形初始结构选取等研究中的重要性,本文针对基于面形斜率的高斯径向基表征模型,研究了不同的采样点分布类型对该模型面形拟合精度的影响。采用不同采样点分布拟合离轴二次曲面和带凸起的抛物面,结果表明采用均匀随机分布的采样点有利于实现高精度的面形拟合,且达到一定的拟合精度后,采样点的数目对拟合精度的影响有限。以离轴三反系统为设计实例,对比了由不同采样方式生成初始面形后系统的像质优化结果。结果显示,采用均匀随机型采样方式得到的初始面形进行系统优化,最终全视场平均调制传递函数(MTF)可以达到0.72以上,远高于由边缘集中采样方式生成初始面形后系统像质的优化结果,从而印证了理论研究结果。
光学设计;自由曲面;拟合精度;采样点分布
1 引 言
随着以超精密金刚石切削技术为代表的现代加工与检测技术的发展,光学自由曲面[1]的研究逐渐走向成熟。光学自由曲面可以在一个表面同时实现多种功能,在提高光学性能、简化结构方面有着非球面无法比拟的优势[2]。然而,自由曲面的面形自由度高,表面矢高变化复杂,对面形表征精度的要求极高,所以面形拟合精度成为自由曲面表征模型的重要研究内容之一[3-4]。自由曲面的表征模型分为两大类:一类是以泰勒函数为代表的有理函数;另一类是以高斯径向基为代表的无理函数[5]。作为典型的有理函数自由曲面表征模型,Zernike多项式的发展较为成熟,但它对大离轴量非对称表面的像差补偿能力有限,很难达到满意的成像质量[6-7]。因此,具有局部面形表征能力的高斯径向基模型成为近些年的研究热点[6-9]。
根据高斯径向基模型的局域性特点,本课题组提出了基于面形斜率的高斯径向基模型(Gaussian Radial Basis Function Based on Slope, Gaussian RBF-BS)[10]。不同于传统高斯径向基模型中所有基函数形状因子数值相同的特点,Gaussian RBF-BS模型中决定模型局域性的形状因子与面形斜率相关联,因此该模型对非对称性表面的拟合精度高出传统高斯径向基模型1-2个数量级,具有更高的面形表征能力[10]。
在光学设计过程中,面形初始结构在一定程度上决定了系统的优化结果和成像质量[11-13],一般利用自由曲面数理模型通过面形拟合方法获得光学自由曲面系统的初始面形。所以,作为光学系统高效优化、快速收敛的一个重要前提,面形拟合精度不仅反映了自由曲面表征模型的面形表征能力,而且影响了系统优化设计中自由曲面的面形初始结构,进而影响最终的优化设计结果。大量研究表明,光学表面的面形拟合精度受到基函数数目和采样点特性等多种因素的影响[14-18]。而高精度面形拟合中,采样点特性对面形拟合精度的影响更加显著,因此国内许多研究组对采样点特性与面形拟合精度的关系进行了研究。冯婕等研究了Zernike多项式项数及采样点数目对拟合精度的影响[14],孙学真研究了抽样点数目对Zernike曲面面形拟合的影响[15],而谢苏泷等则从样项比方面对Zernike多项式曲面拟合进行了研究[16]。这些研究表明,采样点数目是影响拟合精度的重要因素。国外研究组也研究了采样点数目以及分布方式对拟合精度的影响。G W Forbes研究了基于正交基底的自由曲面拟合方法,并分析了面形拟合误差的影响因素[17-18]。Rolland则从拟合精度与采样点分布关系的角度对Zernike多项式以及Q多项式的自由曲面拟合进行了研究。她通过分析比较不同采样点分布类型及采样点数目对Zernike多项式模型面形拟合精度的影响,指出在基函数数量足够的条件下,曲面采样点的分布和数量对拟合过程的收敛速度、计算效率以及面形拟合精度有很大的影响[3-4]。
作者曾对比研究了Gaussian RBF-BS模型和Zernike模型的面形表征能力,并且利用三反系统实例研究了两模型在光学系统设计中的像差平衡能力。研究表明,Zernike模型与Gaussian RBF-BS模型不仅数学表达式截然不同,而且两模型的面形表征能力和像差平衡能力也不同[10]。因此要使具有高自由度的Gaussian RBF-BS模型在光学系统设计中得到更好的应用,研究采样点分布对该模型面形拟合精度的影响具有重要意义。
本文研究了两种采样点分布类型以及采样点数目对Gaussian RBF-BS模型面形拟合精度的影响,通过对比和分析拟合结果确定了适用于Gaussian RBF-BS模型的采样点分布类型,并以离轴三反系统设计为例,分析比较了由不同采样方式生成初始面形后系统的像质优化结果,验证了理论研究结果的正确性。
2 Gaussian RBF-BS模型
光学自由曲面的Gaussian RBF-BS模型表达式为[5]:

(1)

针对传统高斯径向基形状因子取值相同导致的面形拟合能力受限问题[19],本文根据基函数所处位置的面形矢高平均变化率来调整基函数形状因子εi,使εi正比于自由曲面的局部面形斜率。面形矢高变化较大的区域,εi值较大,从而基函数的形状会更为细锐,εi对基函数中心及邻近区域内的矢高拟合贡献较大,而对口径内其他区域矢高拟合的影响较小,拟合行为表现出明显的局域性,因此容易获得较高的面形拟合精度。
3 采样点分布类型及待拟合表面

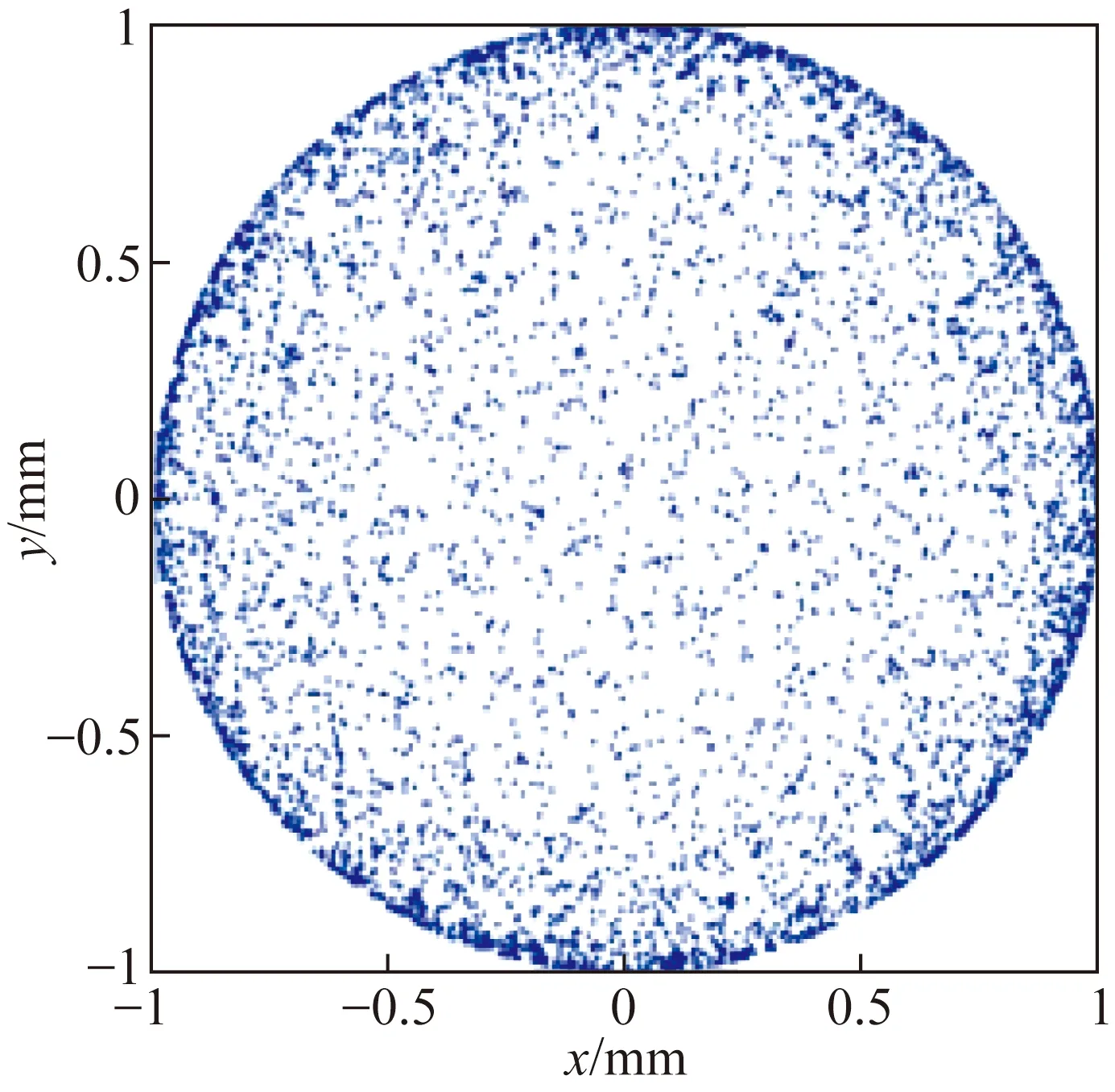
(a)边缘集中型采样点分布

(b)均匀随机型采样点分布
为了研究不同采样点分布类型和数量对Gaussian RBF-BS模型面形拟合精度的影响,选择两种面形进行拟合实验研究。
随着IP技术的发展,大容量计算能力将会带来信号处理方面革新。传统的播出系统在发展到云播出之前,中间的一个重要步骤是一体化播出服务器,其核心技术是将传统播出系统的播出信号、信号切换、键控等功能软件化,运行在通用计算平台上,接口虽然是SDI,但其内部处理完全IP化,配合云计算平台和云处理软件完成整个工作流程。
第一种面形是离轴二次曲面,其面形表达式如下[5]:
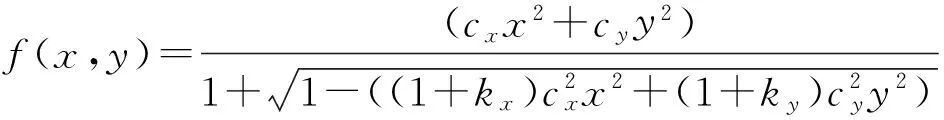
(2)
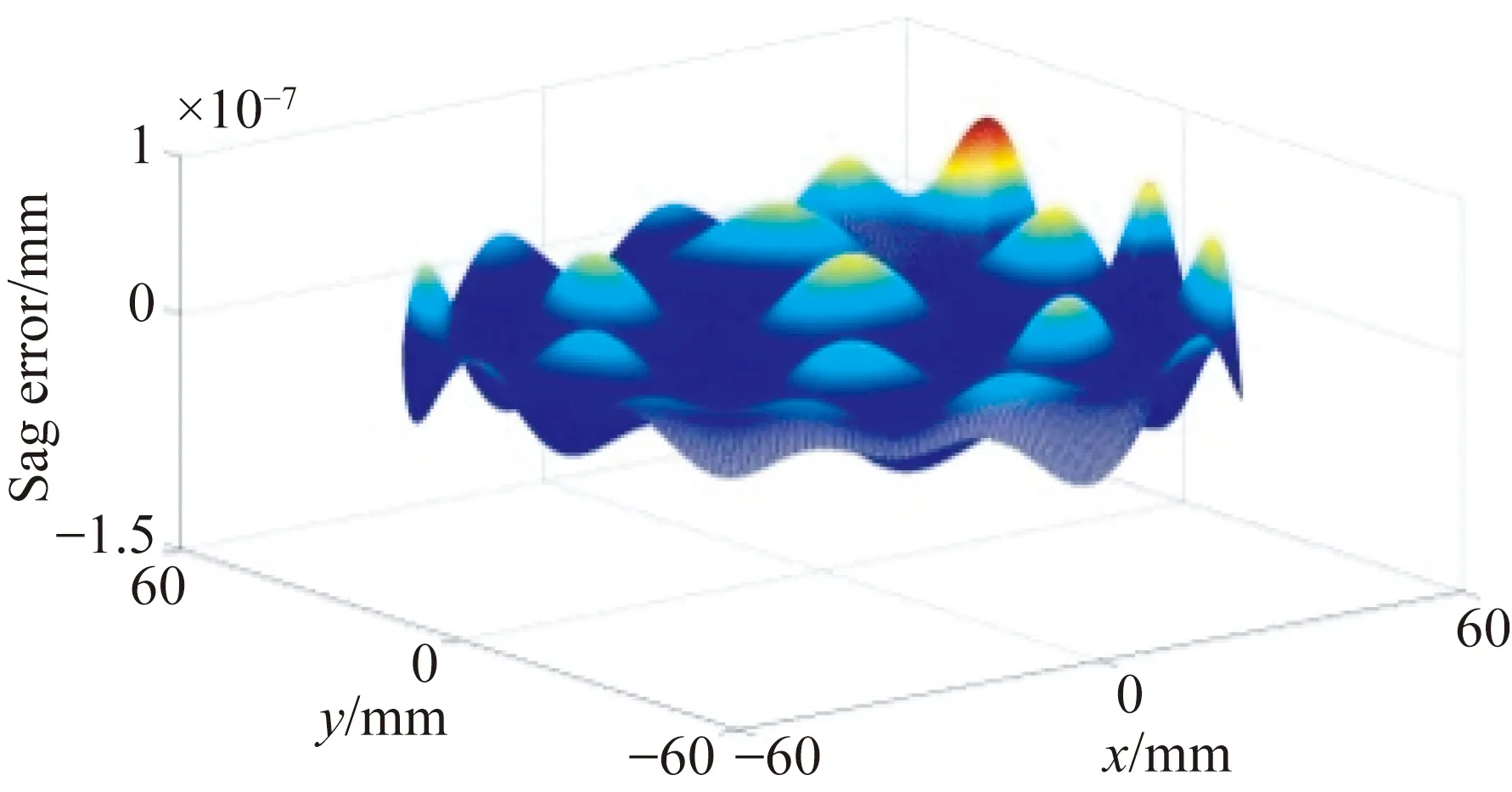
其中:x方向的顶点曲率和非球面系数分别为cx=-1/455.4 mm-1,kx=-1.306;y方向的顶点曲率和非球面系数分别为cy=-1/455.4 mm-1,ky=-1.306;有效口径为110 mm,离轴量为50 mm。该自由曲面的矢高如图2所示。
图2 离轴二次曲面的面形矢高
第二种面形是带凸起的抛物面。该面形具有一定的普适性[15],不仅包含二次曲面项,还包含不同函数中心的高斯项,位置分别位于0.92口径处、0.36口径处(凸起程度最大)和0.86口径处。因此,这个表面既有位于口径边缘的凸起,又有位于口径内部的凸起。其面形表达式如下[5]:
0.6e-0.49[(x+3)2+(y-2)2]+0.03e-0.81[(x-5)2+(y-7)2].
(3)
单位口径内,该自由曲面的矢高如图3所示。与离轴二次曲面相比,该表面在口径内部具有较大的矢高变化,即面形斜率变化较大,因此其高精度的面形拟合的难度也更大。

图3 带凸起的抛物面面形矢高
4 面形拟合结果及分析
实验中,均匀随机分布和边缘集中分布两种采样点分布类型生成采样点坐标,然后利用Gaussian RBF-BS模型对上述两种面形进行面形拟合,最后通过计算所有采样点拟合误差的均方根来评估模型的面形拟合精度。
(a)均匀随机分布采样点拟合后的面形矢高差
(b)边缘集中分布采样点拟合后的面形矢高差
(c)不同采样点分布类型的面形拟合精度随采样点数目的变化
(c)Fitting precision versus number of sampling points for different distribution of sampling points
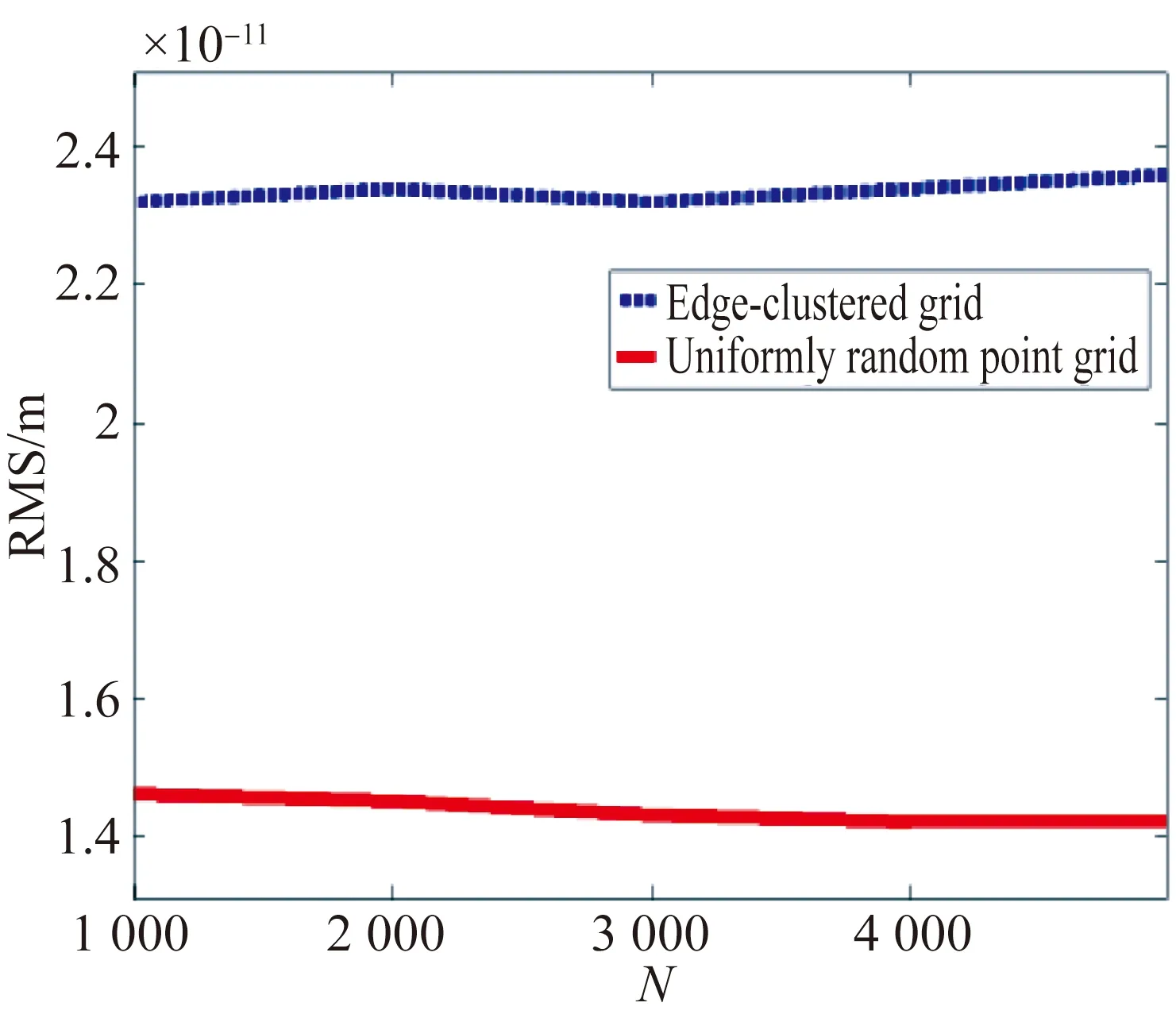
图4使用不同采样点分布的离轴二次曲面面形拟合结果
Fig.4Fitting results of off-axis quatric surface by using sampling points in different distributions
图4(c)是不同采样点分布类型的面形拟合精度随采样点数目的变化曲线。从图4(c) 可以看出,在Gaussian RBF-BS模型拟合离轴二次曲面的过程中,上述两种采样点分布类型最终均可得到比较满意的拟合结果,拟合精度达到了10-11m 量级。在采样点数目相同的条件下,与均匀随机型采样点分布相比,边缘集中型采样点分布面形拟合后的RMS值更高,即采用均匀随机采样点分布进行面形拟合能够获得更高的面形拟合精度。这一结果从图4(a) 和4(b)的矢高差分布情况也可明显看出。同时随着采样点数目的增多,使用两种采样点分布类型进行面形拟合后的RMS数值变化幅度较小,这说明达到一定的拟合精度后,采样点数量对模型面形拟合精度的影响并不明显。
图5是Gaussian RBF-BS模型拟合带凸起的抛物面的结果。由于面形矢高变化较大,拟合难度较高,需要使用更多的基函数才能获得较高的拟合精度。图5(a)、5(b)分别为采样点数目为3 000 个,基函数为729项时,以均匀随机型分布和边缘集中型分布方式在全口径内拟合得到的带凸起抛物面的面形矢高差。图5(c)是不同采样点分布类型的面形拟合精度随采样点数目的变化曲线。从图5(c)可以看出,在Gaussian RBF-BS模型拟合带凸起的抛物面时,随着采样点数目的增多,拟合精度呈现先提高后不变的趋势。采样点数目不足会导致凸起抛物面面形矢高变化较大的凸起处欠采样,从而影响拟合精度。当采样点数目超过2 000个时,最终的拟合精度能达到nm量级,拟合精度不再受采样点数目的影响,采样点分布成为决定拟合精度的主要因素之一。因此,在此拟合精度下,相同的采样点数目,边缘集中型采样点分布进行面形拟合后的RMS数值同样高于均匀随机型采样点分布,即边缘集中型采样点分布的拟合精度低于均匀随机型采样点分布的拟合精度。
综合两类面形的拟合分析结果可知,Gaussian RBF-BS模型要达到一定的面形拟合精度,需要足够的采样点数量,并且拟合过程中采样点应呈均匀随机型分布。在达到一定的拟合精度后,采样点数目对拟合精度的影响不明显,而过多的采样点数量会增加拟合运算量,降低拟合效率。已有研究表明,传统的Zernike多项式模型使用边缘集中型采样点分布更有利于提高面形拟合精度[3]。因此,采样点分布方式对基于不同自由曲面表征模型的面形拟合精度的影响是不相同的。
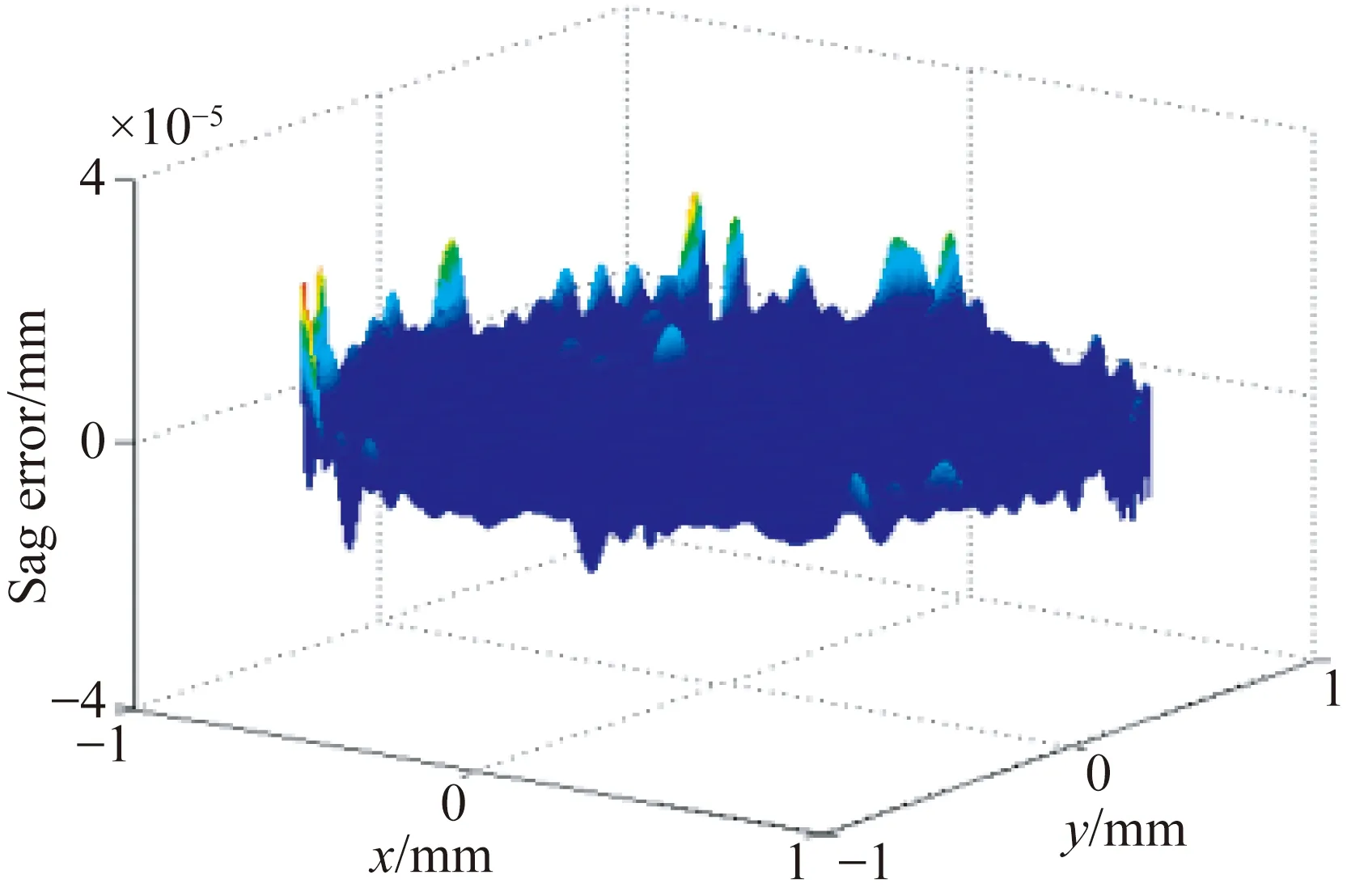
(a)均匀随机分布采样点拟合后的面形矢高差
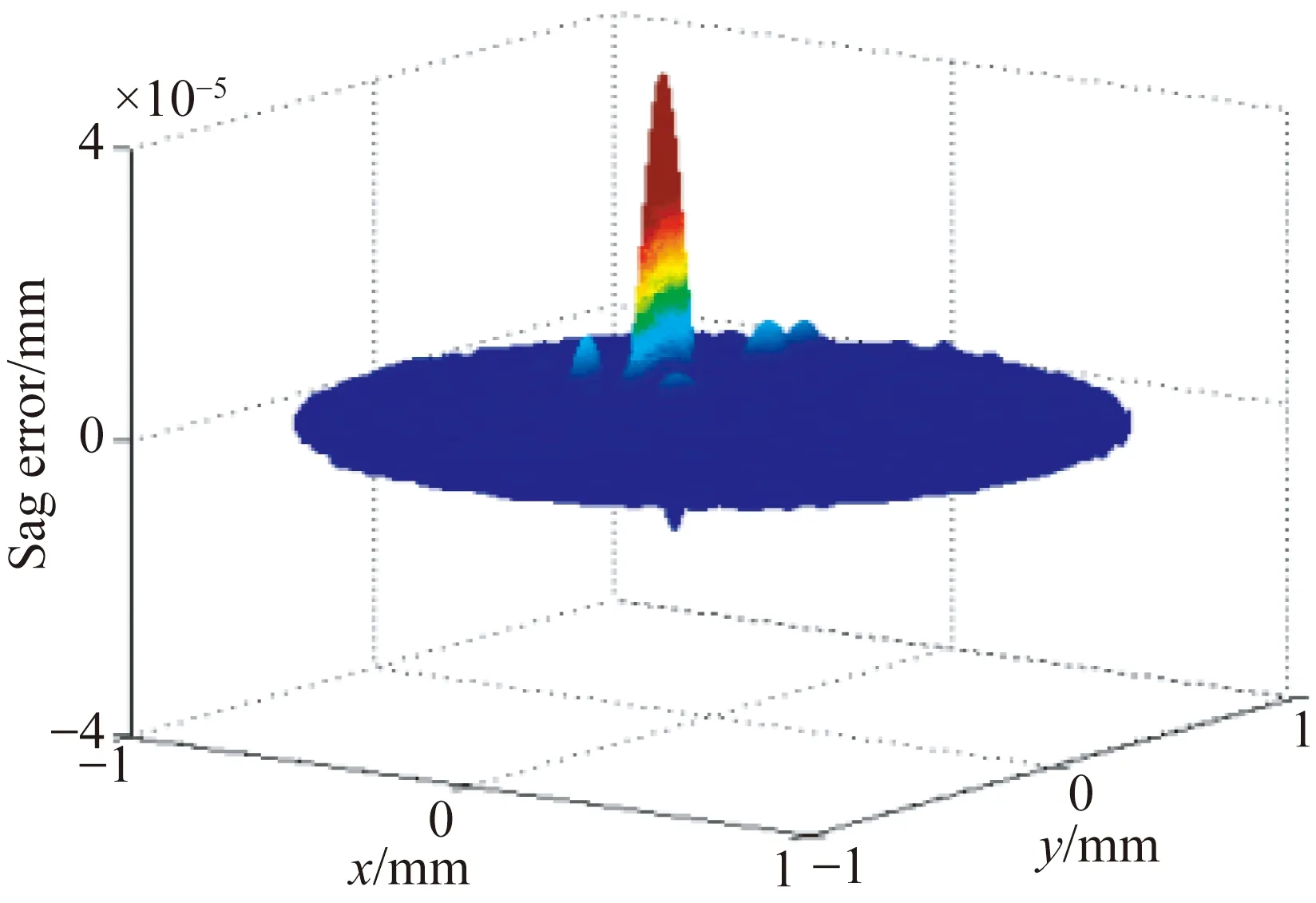
(b)边缘集中分布采样点拟合后的面形矢高差
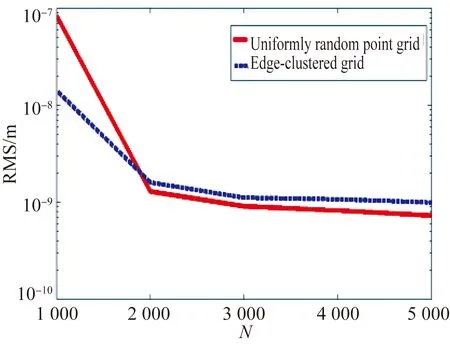
(c)不同采样点分布类型的面形拟合精度随采样点数目的变化
(c)Fitting precision versus number of sampling points for different distribution of sampling points
图5使用不同采样点分布的带凸起的抛物面面形拟合结果
Fig.5Fitting results of bumpy paraboloid surface by using sampling points in different distributions
采样点分布方式对Gaussian RBF-BS模型和Zernike多项式模型面形拟合精度的影响之所以出现完全不同的结果,其原因在于Zernike多项式模型是一种全局性表征模型,拟合过程中矢高差通常在口径边缘处显著增大,因此边缘集中型采样点分布将增加口径边缘处的采样点个数(如图1(a)所示),从而有利于面形拟合精度的提高。而Gaussian RBF-BS模型是一种具有局域性的表征模型,通过设置与面形斜率相关的形状因子,使得拟合过程中的矢高差在口径内呈现相对均匀的分布特性,如图4(a)、4(b)和图5(a)、5(b) 所示。如果采用边缘集中分布的采样点,会造成拟合过程中的口径内欠采样,反而降低了全口径的拟合精度,而均匀随机分布的采样点则明显有利于面形拟合精度的提高。随着面形拟合精度的提高,拟合结果会越接近理想面形。因此,在光学系统设计过程中,采用均匀随机分布方式获得的初始结构进行系统像质优化可以得到更好的像质。
5 设计实例
为了进一步说明不同采样点分布方式对面形表征和系统设计中初始结构求解的影响,本文以离轴三反系统为例,对系统中的三镜分别采用由不同采样点分布方式得到的两种RBF-BS自由曲面进行面形表征及系统优化,比较系统设计结果的成像质量。在面形表征过程中,基函数有64项,采样点数目为4 000个。
离轴三反系统结构如图6所示。其中三镜的半口径为50 mm,系统的有效焦距为110 mm,设计工作波长为632.8 nm,视场为±1.2°×±1°,这里在二维视场中选取14个视场点对系统像质进行综合考察。
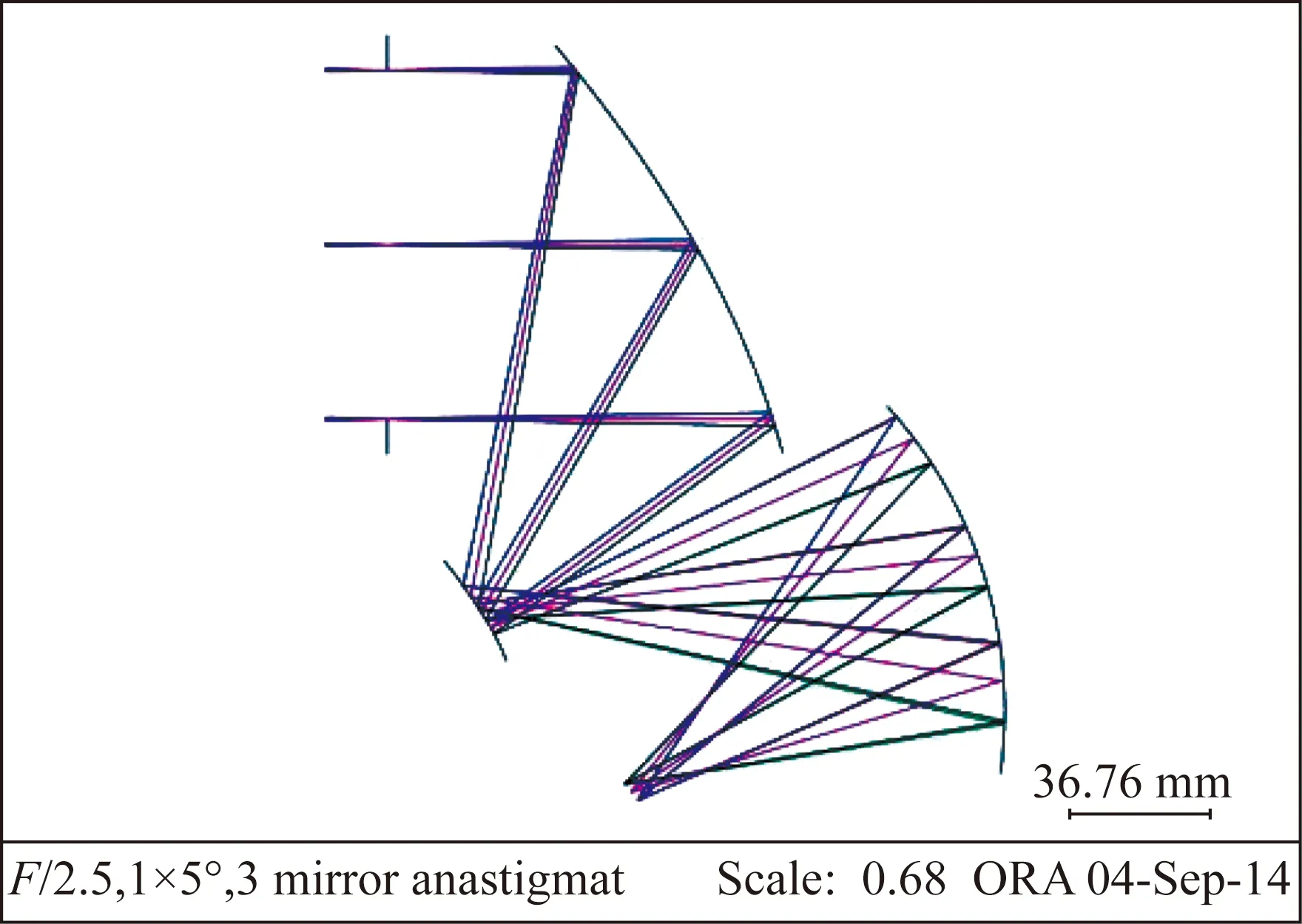
图6 离轴三反系统结构图
Fig.6Schematic diagram of Three Mirror Anastigmat(TMA) system
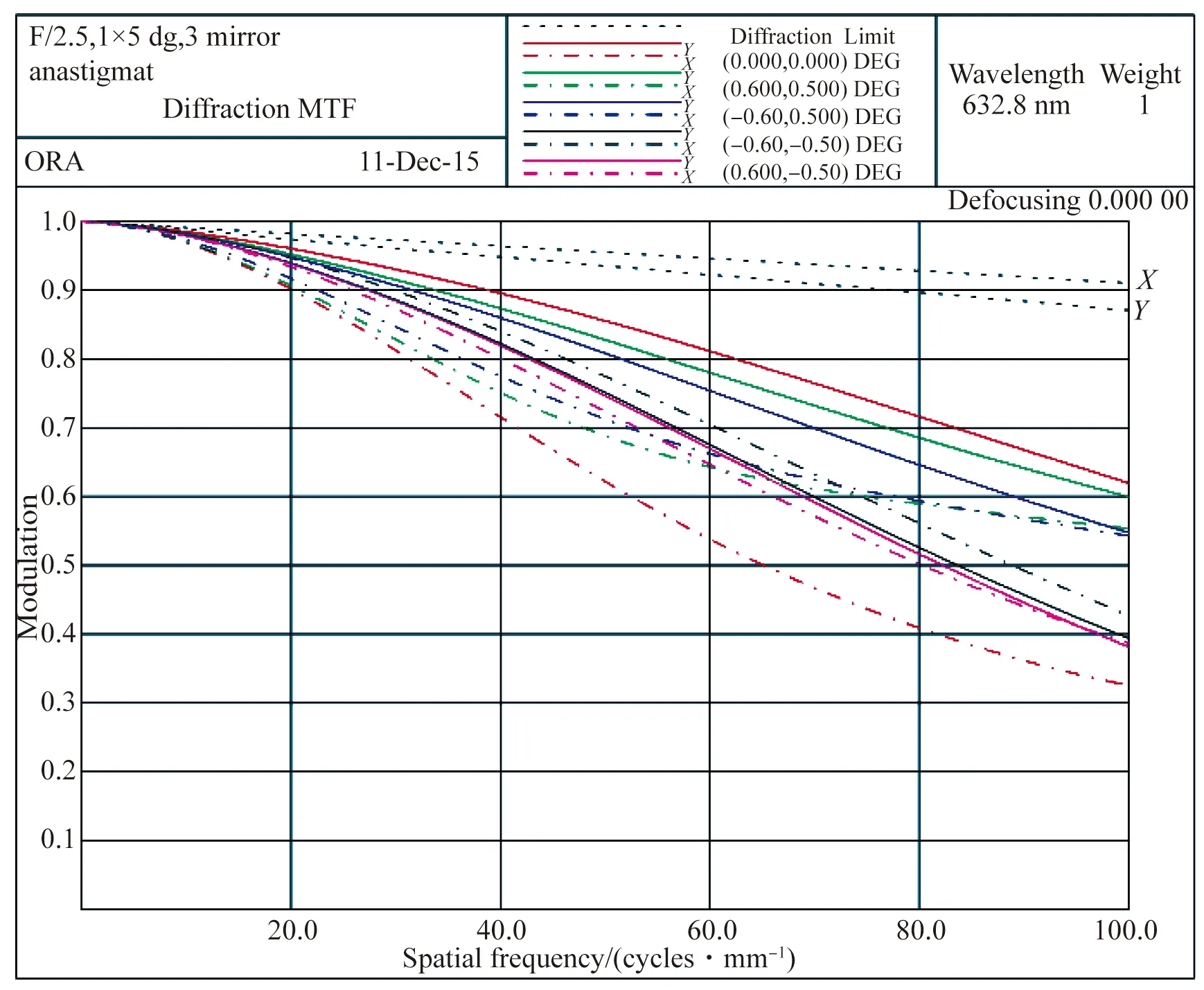
本文采用光学设计软件Code V对系统进行像质优化及评估。系统三镜的初始结构是采用两种不同采样点分布方式通过面形拟合得到的两个RBF-BS自由曲面表面,面形拟合矢高差如图7所示,自由曲面的面形参数是由软件面形自定义模块导入的。这里选取全视场在100 lp/mm 处的平均MTF、最大畸变量和全视场平均波像差作为评估系统成像质量的标准。在相同的优化条件与环境下,经过相同的优化步骤得到的系统MTF曲线图8所示,两种采样点分布方式得到的像质如表1所示。

(a)均匀采样
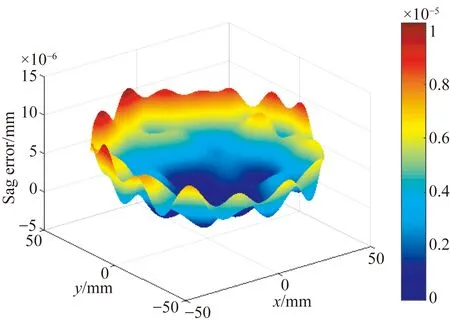
(b)边缘集中采样

DistributionMaxdistortion/%AverageMTFYRMSWFE(λ)Uniformlyrandomdistribution2.3672.6140.18877Edge-clustereddistribution2.7641.0390.41716
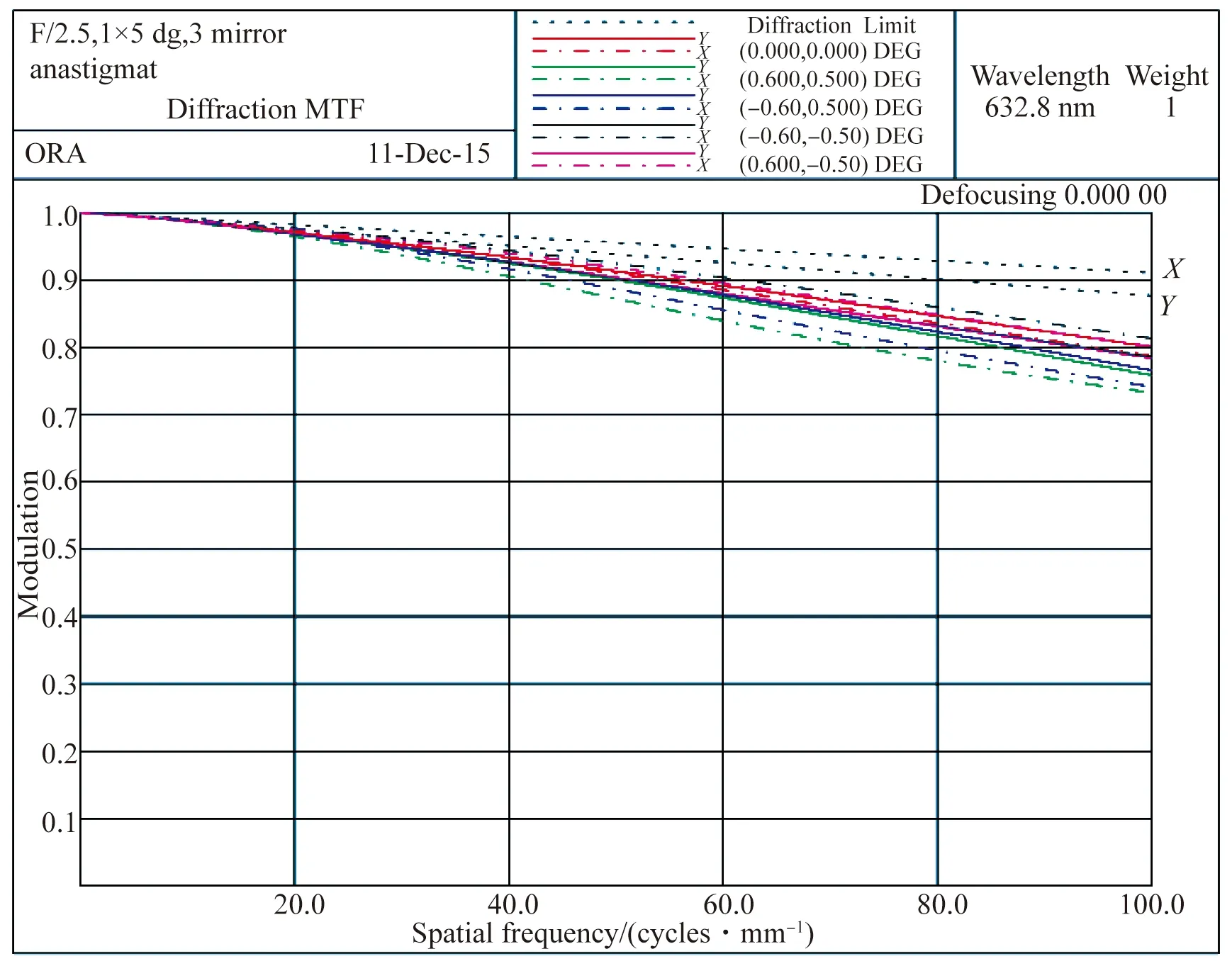
(a)采用均匀采样方式得到的初始面形对应系统MTF曲线
(a)MTF curve of system with initial surface which generated by uniformly random grid
(b)采用边缘集中采样方式得到的初始面形对应系统MTF曲线
(b)MTF curve of system with initial surface which generated by edge-clustered grid
图8两种初始面形用于离轴三反系统的像质对比
Fig.8Comparison of image quality of two initial surfaces used in TMA system
由设计结果可知,采用均匀随机型采样方式得到的初始面形在进行系统优化后,MTF达到0.72以上,最大畸变量为2.36%。由于采用均匀随机型采样点分布方式的面形拟合精度更高,矢高误差相对较小,所以得到的初始面形更接近于理想面形。因此,对于口径内矢高变化较为剧烈的三镜,采用均匀随机型采样点分布方式拟合得到的初始面形更容易获得理想像质。这与上述理论分析结果相一致。
6 结 论
本文针对基于Gaussian RBF-BS模型研究了两种不同的采样点分布类型,即均匀随机型采样点分布和边缘集中型采样点分布,对Gaussian BF-BS模型拟合自由曲面的面形拟合精度的影响。通过比较不同采样点分布条件下离轴二次曲面和带凸起的抛物面的拟合结果可以发现,均匀随机型采样点分布的面形拟合精度比边缘集中型采样点分布的面形拟合精度高,并且达到一定的拟合精度后,采样点的数目不再影响拟合精度,而过多的采样点数量则会增加拟合运算量,降低拟合效率。这一结果不同于已有的关于Zernike多项式模型的研究报道,对Gaussian RBF-BS模型在自由曲面表征和设计中的应用具有一定的理论指导意义。最后,以离轴三反系统设计为例,分析比较由不同采样方式生成初始面形后系统的像质优化结果。结果显示,采用均匀随机型采样方式得到的初始面形在进行系统优化后,最终全视场的平均调制传递函数(MTF)达到0.72以上,远高于由边缘集中采样方式生成初始面形后系统像质的优化结果。
[1]THOMPSON K P, ROLLAND J P. Freeform optical surfaces: a revolution in imaging optical design [J].Opt.Pho.News, 2012, 23(6): 30-35.
[2]FUERSCHBACH K, JANNICK P R, KEVIN P T. A new family of optical systems employingφ-polynomial surfaces [J].Opt.Express, 2011,19(22): 21919-21928.
[3]ILHAN K, KEVIN P T, JANNICK P R. Edge clustered fitting grids forφ-polynomial characterization of freeform optical surfaces[J].OpticalExpress, 2011,19(27): 26962-26974.
[4]ILHAN K, KEVIN P T, JANNICK P R. Comparative assessment of freeform polynomials as optical surface descriptions[J].Opt.Express, 2012,20(20): 22683-22691.
[5]王超.自由曲面表征函数及其应用研究[D].长春:中国科学院长春光学精密机械与物理研究所, 2014.
WANG CH.ResearchonCharacterizationFunctionandApplicationofFree-formSurface[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2014.(in Chinese)
[6]OZAN C, ILHAN K, GREGORY E F,etal.. Application of radial basis functions to represent optical freeform surfaces [J].SPIE-OSA,2010, 7652:76520A-1.
[7]OZAN C, GREGORY E F, HASSAN F,etal.. Meshfree approximation methods for free-form surface representation in optical design with applications to head-worn displays [J].SPIE,7061: 70610D.
[8]OZAN C, BRENDAN M, HASSAN F,etal.. Optimal local shape description for rotationally non-symmetric optical surface design and analysis[J].OpticalExpress, 2008,16(3): 1583-1589.
[9]OZAN C, SOPHIE V, HASSAN F,etal.. Application of radial basis functions to shape description in a dual-element off-axis magnifier[J].OpticalLetter, 2008,33(11): 1237-1239.
[10]赵星,郑义,张赞,等. 基于面形斜率的光学自由曲面表征[J].光学 精密工程,2015,23(7):1954-1964.
ZHAO X, ZHENG Y, ZHANG Z,etal.. Characterization of freeform optical surfaces based on surface slope [J].Opt.PrecisionEng., 2015,23(7):1954-1964.(in Chinese)
[11]张博,王凌,常伟军,等. 头盔显示器自由曲面光学组件的优化设计[J].应用光学,2014,35(2):193-197.
ZHANG B, WANG L,CCHANG W J,etal.. Optimal design of free-form-surface optical component in helmet mounted display[J].JournalofAppliedOptics,2014,35(2):193-197.(in Chinese)
[12]晏蕾,贾平,洪永丰.红外双视场光学系统的初始结构求解[J].红外,2011,32(1):23-26.YANG L, JIA P, HONG Y F. Design of initial structure of infrared dual field-of-view optical system [J].Infrared,2011,32(1):23-26.(in Chinese)
[13]崔恩坤,张葆,洪永丰,等.PW 法对连续变焦光学系统初始结构的求解[J].应用光学,2014(4):586-591.
CUI E K, ZHANG B, HONG Y F,etal.. Design of initial structure of infrared zoom optical system with PW solution [J].JournalofAppliedOptics, 2014(4):586-591.(in Chinese)
[14]冯婕,白瑜,邢廷文,等.Zernike多项式波面拟合精度研究[J].光电技术应用,2011,26(2):31-34.FENG J, BAI Y, XING T W,etal..Fitting accuracy of wavefront using Zernike polynomials [J].Electro-OpticTechnologyApplication, 2011,26(2):31-34.(in Chinese)
[15]孙学真,苏显渝,荆海龙,等.抽样点对基于Zernike多项式曲面拟合精度的影响[J].光学仪器,2008,30(4):6-10.SUN X ZH, SU X Y, XING H L,etal.. The influence of sampling points on the precision of curved surface fitting based on Zernike polynomials [J].OpticalInstruments, 2008,30(4):6-10.(in Chinese)
[16]谢苏隆.Zernike多项式拟合曲面中拟合精度与采样点数目研究[J].应用光学,2010,31(6):943-949.XIE S L. Sampling point number in curved surface fitting with Zernike polynomials [J].JournalofAppliedOptics, 2010,31(6):943-949.(in Chinese)
[17]FORBES G W. Shape specification for axially symmetric optical surfaces [J].Opt.Express,2007,15:5218-5226.
[18]FORBES G W. Robust, efficient computational methods for axially symmetric optical aspheres [J].Opt.Express,2010,18: 19700-19712.
[19]OZAN C, BRENDAN M, HASSAN F,etal.. Optimal local shape description for rotationally non-symmetric optical surface design and analysis[J].OpticalExpress, 2008,16(3): 1583-1589.
[20]鄢静舟,雷凡,周必方,等.用Zernike多项式进行波面拟合的几种算法[J].光学 精密工程,1999,7(5): 119-128.
YAN J ZH, LEI F, ZHOU B F,etal.. Several algorithms for wavefront fitting using Zernike polynomails[J].Opt.PrecisionEng., 1999,7(5): 119-128.(in Chinese)

武鹏飞(1968-),男,辽宁兴城人,博士,教授,1996年于南开大学获得博士学位,主要从事光学信息处理等方面的研究。E-mail: pwu@nankai.edu.cn

赵星(1980-),男,北京人,博士,副教授,2007年于南开大学获得博士学位,主要从事光学信息处理以及光学系统设计等领域的研究工作。E-mail: zhaoxingtjnk@nankai.edu.cn
(版权所有未经许可不得转载)
Influence of sampling point distribution in freeform surfaces fitting with radial based function model
WU Peng-fei1, ZHANG Zan1,ZHENG Yi1, ZHANG Juan1, WANG Yao-yao1, ZHAO Xing1*, WANG Ling-jie2, WU Yan-xiong2
(1.InstituteofModernOptics,KeyLaboratoryofOpticalInformationScienceandTechnology,MinistryofEducation,NankaiUniversity,Tianjin300071,China;2.KeyLaboratoryofOpticalSystemAdvancedManufacturingTechnology,ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China)
*Correspondingauthor,E-mail:zhaoxingtjnk@nankai.edu.cn
In view of the importance of surface shape fitting precision of free-form surface model in researches such as free-form surface representation and selection of initiating structure of surface shape, the influence of different sampling point distribution patterns on surface shape fitting precision of the Gaussian Radial Basis Function Based on Slope( Gaussian RBF-BS) model was investigated. An off-axis quadric surface and an bumpy paraboloid were fitted with different sampling point distributions which were uniformly random points and edged-clustered points. The results show that the uniformly random grid is better for surface shape fitting due to the high precision. The influence of sampling point quantity on fitting precision remains constant when certain fitting precision is reached. The off-axis Three Mirror Anastigmat(TMA) system was optimized experimentally by using initial surface shapes generated with different sampling methods. The results show that, by using initial surface shape generated from uniformly random sampling method for the system optimization, the average Modulation Transfer Function (MTF) of whole field of view is more than 0.72, which is much higher than that by using surface shape generated by edge cluster sampling points. Thus the theoretical research results were verified.
optical design; freeform surface; fitting precision; distribution of sampling points
2016-03-04;
2016-04-29.
国家自然科学基金资助项目(No.11474169);中科院科技创新基金重点项目;天津市应用基础与前沿技术研究计划资助项目(No.15JCYBJC16900)
1004-924X(2016)07-1564-09
TH703
Adoi:10.3788/OPE.20162407.1564

