高分辨率4f传像系统分辨率的影响因素分析

夏春秋，钟　兴，刘春雨，韩培仙1，，金　光

(1.中国科学院大学，北京 100049；2.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；3.长光卫星技术有限公司，吉林 长春 130031)



高分辨率4f传像系统分辨率的影响因素分析

夏春秋1，2*，钟兴2，3，刘春雨2，韩培仙1，2，金光2

(1.中国科学院大学，北京 100049；2.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；3.长光卫星技术有限公司，吉林 长春 130031)

研究了在实际应用中4f传像系统分辨率的影响因素及其作用机制，用于指导系统的设计和装调。首先，在理论上分析了由装调误差引起的像差对系统光学传递函数(MTF)产生的影响，并建立了描述二者关系的数学模型。基于该模型研究了1 μm分辨率4f光学系统的装调误差，仿真计算了系统含有透镜偏心、倾斜、位移误差对MTF的影响，得到了分辨率随误差的变化曲线。实验结果表明，倾斜在15″以内，偏心误差在0.02 mm，位移在0.01 mm范围内，装调误差均会导致分辨率下降，虽然倾斜在极小范围内微调时分辨率会提高，但总的变化趋势不变。绘制的装调误差与分辨率的关系图，可为高分辨率4f系统的误差预估提供参考。

信息光学；4f传像系统；装调误差；数学模型；曲线分析；高分辨率

1　引　言

光学信息处理是以信息光学为基础，用傅里叶分析的方法研究光学成像和光学变换的技术[1-2]。4f系统的相干光空间滤波是光学信息处理的重要实现系统之一。它以二维图像作为媒介来实现图像的识别、图像的增强与恢复、图像的传输与变换、功率谱分析以及全息术中的傅里叶全息存储等，因此在图像光学小波变换、数字全息及工件误差检测、粒子测量等领域有着广泛的应用[3-5]。

根据所需要处理的图形或者工作内容不同，4f系统设计主要考虑待处理输入面的尺寸和所需的最高空间频率及镜头负担等问题。目前，4f系统的分辨率为1 μm左右。

随着光学信息处理器件的发展，4f系统越来越多地与数字计算机结合使用，其应用前景也更加广阔，并且随着图像精度需求的提高，分辨率的要求也越来越高。分辨率性能的优劣直接影响到光学信息处理结果的好坏，它作为成像质量判断的一个重要指标，在设计、装调中具有指导意义。本文详细讨论了影响4f系统分辨率的主要因素，建立了影响高分辨4f传像系统分辨率的主要因素的数学模型，基于该模型对1 μm分辨率的4f光学系统进行了全面的对比分析和评价，从而提高了实际装调和图像处理的效率。

2　4f传像系统分辨率的影响因素分析

图1所示为4f系统的结构示意图。其中，S为照明点，光源L为准直透镜， L1，L2分别为第一、第二傅里叶变换透镜，P1为物面，P为频谱面，P2为系统像面。由于4f系统是小像差光学系统，所以采用分辨率板和点列图很难有效地衡量其分辨率。调制传递函数(Modulation Transfer Function，MTF)曲线表示不同频率的正弦强度分布函数，即(物体)经光学系统成像后其对比度的衰减程度。它既与光学系统像差有关，又与光学系统的衍射效果有关，能同时运用于小像差光学系统和大像差光学系统。因此这里采用MTF曲线作为4f系统分辨率的判断依据。

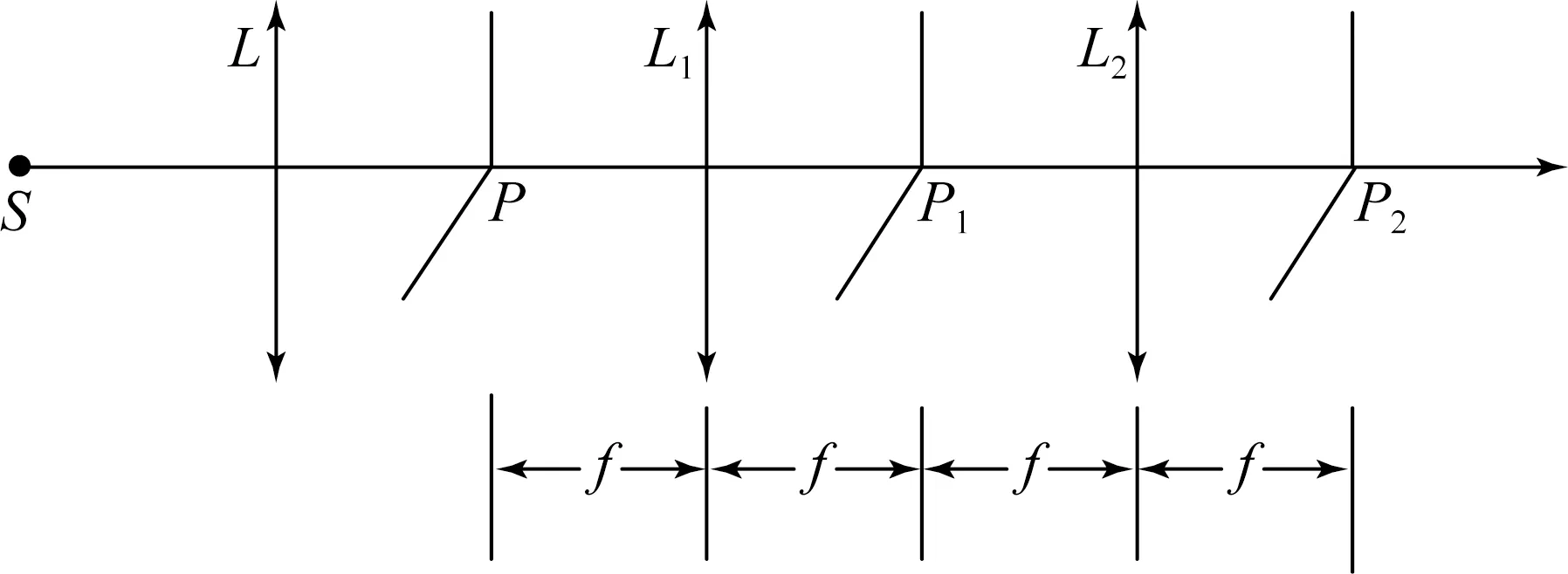
图1　4f系统结构示意图

光学系统的误差来源主要有光学、机械两方面。其中，光学误差主要包括加工工艺引起的半径厚度、偏心等偏差；光机加工、装调中的误差可以概括为元件的厚度偏差、位移、偏心和倾斜等。在实际系统中，透镜系统的结构参数如曲率半径、厚度等是确定的，各光学面的曲率半径和面形、玻璃材料的质量等级都能控制在所要求的公差之内，即使存在面型误差，也可以通过微调间距使系统满足共轴公差要求。因此跟辅助装调有关的变量，如光学面之间的空气间隔、光学面的倾斜与偏心等成为引起系统像质变化的主要因素。

实际实验得到的与位移、偏心、倾斜等因素相关的结论如下：

(1)光路是否共轴。光通过透镜不同的地方，因为透镜的厚度不同，从而使得位相调制函数不同，而影响成像效果；

(2)光通过傅氏透镜的中心后，能否将亮斑完全照射到成像面上，使得图像成像完整；

(3)物面、像面的摆放位置是否严格遵守4f透镜的要求。

在明确装调误差是4f系统分辨率的主要影响因素之后，通过建立装调误差和MTF的数学模型来探究4f分辨率影响因素及其影响机制，对高分辨率4f系统的误差预估工作有指导意义[6]。

3　影响因素与MTF的数学关系模型

如图2所示，当成像系统成像时，出瞳的理想面为So，像差W(x，y)的存在导致实际波面S偏离了球面。此时出瞳面上的透过率函数(即光瞳函数)为：

P(x，y)=P(x，y)exp[jkW(x，y)].

(1)

根据式(1)，系统的通频带范围仍由光瞳尺寸决定，截止频率和像差无关。但是像差在通带内引入了与频率有关的相位畸变，会影响像质。而在实际光学系统的MTF曲线中，满足某观察对比度的截止频率代表了系统的分辨能力。

图2　波像差示意图

在光学系统中，波像差W(x，y)可用Zernike多项式进行描述：

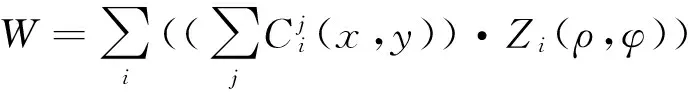
(2)

表1　Zernike多项式的表述

一般采用Zernike多项式系数Z5，Z6，Z7，Z8，Z9作为系统成像质量的评价标准。当存在上述失调量时，光学系统会产生像差，用Zernike多项式来表示像差，那么它与失调量之间的函数关系为：

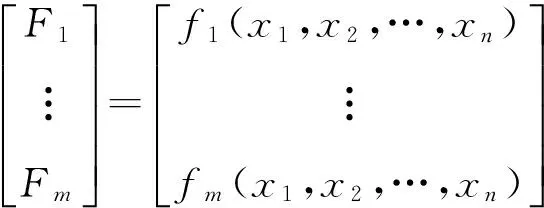
(3)

其中：Fj(j=1，2，3，…，n)为系统像差，xi(i=1，2，3，…，n)为各元件位置的结构参量，fj(j=1，2，3，…，n)代表像差与镜面位置之间的函数关系[7-8]。

经过泰勒展开变换，像差与位置结构参量变化之间的近似线性方程组为：

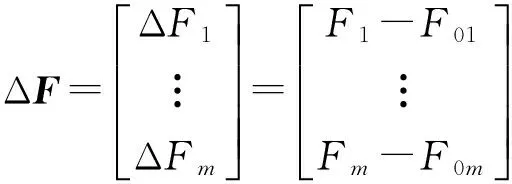
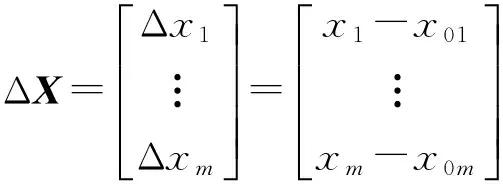
(4)

式(4)可化为失调量与像差之间的数学模型：

A·ΔX=ΔF，

(5)

式中：A为灵敏度矩阵；ΔX为系统中各片镜面需要调整的变化量，即失调量。失调量通常包括沿垂直于光轴方向的移动量、转动量及各镜面之间的轴向间隔(TEDY、TETX、TETY)；ΔF为各校正对像的实测值与光学设计值之差，也就是系统成像质量随失调量的变化值。因此已知失调量引起的像差，可以采用波像差理论和MTF建立数学模型，MTF作为光学调制传递函数，可以用傅里叶级数或积分的形式表述，从而得到失调量对分辨率的影响。

根据4f系统傅里叶变换的规则，用瞳孔位置坐标相关的泽尼克多项式表达波像差[8-9]，即有：

(6)

a3(x2+y2)+a4(y2-x2)+a5(xy)+

a6[-2x+3x(x2+y2)]+

a7[-2y+3y(x2+y2)]+

a8[1-6(x2+y2)+6(x2+y2)]2+…，

(7)

式中：an为Zernike多项式的展开系数，Zn(ε，η)为Zernike多项式。各多项式的物理意义分别对应表1中的2～9项。由于在4f传像系统的实际使用过程中通常有光阑限制，这种情况下的Zernike高阶像差很小，对成像的影响也很小，因此主要讨论该公式中Zernike的前8项像差，即对其初级像差进行讨论和研究。

本文以x，y方向均存在倾斜像差的4f系统为例，用Zernike多项式将式(7)与装调和加工引起的像差联系起来，得到系统的出瞳函数为：

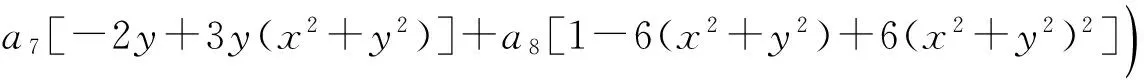
(9)

这时出瞳面上的透过率函数(即光瞳函数)为：

Hc(fx，fy)=P(λdifx，λdify)=

P0(λdifx，λdify)exp(jkW(λdifx，λdify)).

(10)

其波相差为：

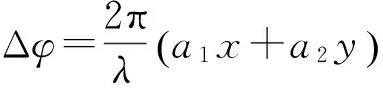
(11)

在理想情况下光瞳是圆形光斑，其表达式为：

(12)

其中r为光瞳半径。则有：

P(ε，η)=P0(ε，η)·exp[jkW(x，y)]=

(13)

脉冲响应为光瞳函数的傅里叶变换：

H=F{Δφ}=F{P(ε，η)}=

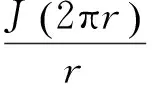
(14)

在实际脉冲响应的计算过程中，相干脉冲响应不再单纯是孔径的夫琅禾费衍射图样，必须考虑波像差的影响。如式(14)所示，虽然倾斜像差不改变截止频率只产生像点位移，但更高级次的像差会在通带内引入与频率有关的相位畸变，使像质变坏。因此在分析像差对分辨率的影响时，以MTF函数作为分析依据具有对小像差系统敏感的优点，同时更加客观和可靠。MTF为脉冲响应模的归一化形式，即：

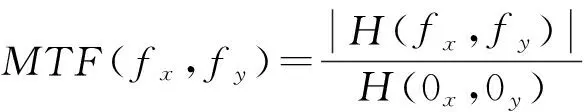
(15)

将式(14)的脉冲响应代入式(15)，根据MTF曲线的值可以得到某一对比度下系统的空间频率，即分辨率的倒数。

4f系统属于小像差系统，因此Zemax中MTF曲线一般用FFT MTF表示。快速傅里叶变换(Fast Fourier Transform，FFT)是对连续变换的信息进行采样然后再根据离散信号进行频谱计算。在分析偏心、倾斜、位移误差对实际装调测量的光学系统分辨率的影响时，首先对装调允许范围内的误差进行采样，然后结合ZEMAX和MATLAB通过FFT MTF计算[10-11]可以得到误差引起的4f系统某一观察对比度要求下的空间频率f，分辨率为空间频率的倒数。其流程如图3所示。

图3　MTF计算的流程图

在实际分析过程中，同样的元件误差在不同透镜上作用，引起的分辨率改变值是不同的。为了探究特定种类的误差对整个系统分辨率的影响，这里采用“均方根”的方法。若一片透镜的某一种误差量为a，引起整个系统分辨率的变化值为x1，假设含有某误差量为a的系统中有k片透镜，则透镜L1至Lk每一片透镜分别带有误差a，系统所表现的分辨率误差即为x1，x2，…，xk。通过均方根的形式推导出当系统含有误差量a时分辨率的变化量，即分辨率为：

(16)

通过分析该方法设置系统中某透镜含有的单一误差，可以求得在特定误差值下系统分辨率的均值，从而可以设置不同的误差值来观察分辨率随误差的变化。这对探究高分辨4f系统的分辨率影响因素及实际使用中误差对系统分辨率的影响程度具有指导意义。具体的计算流程如图4所示。

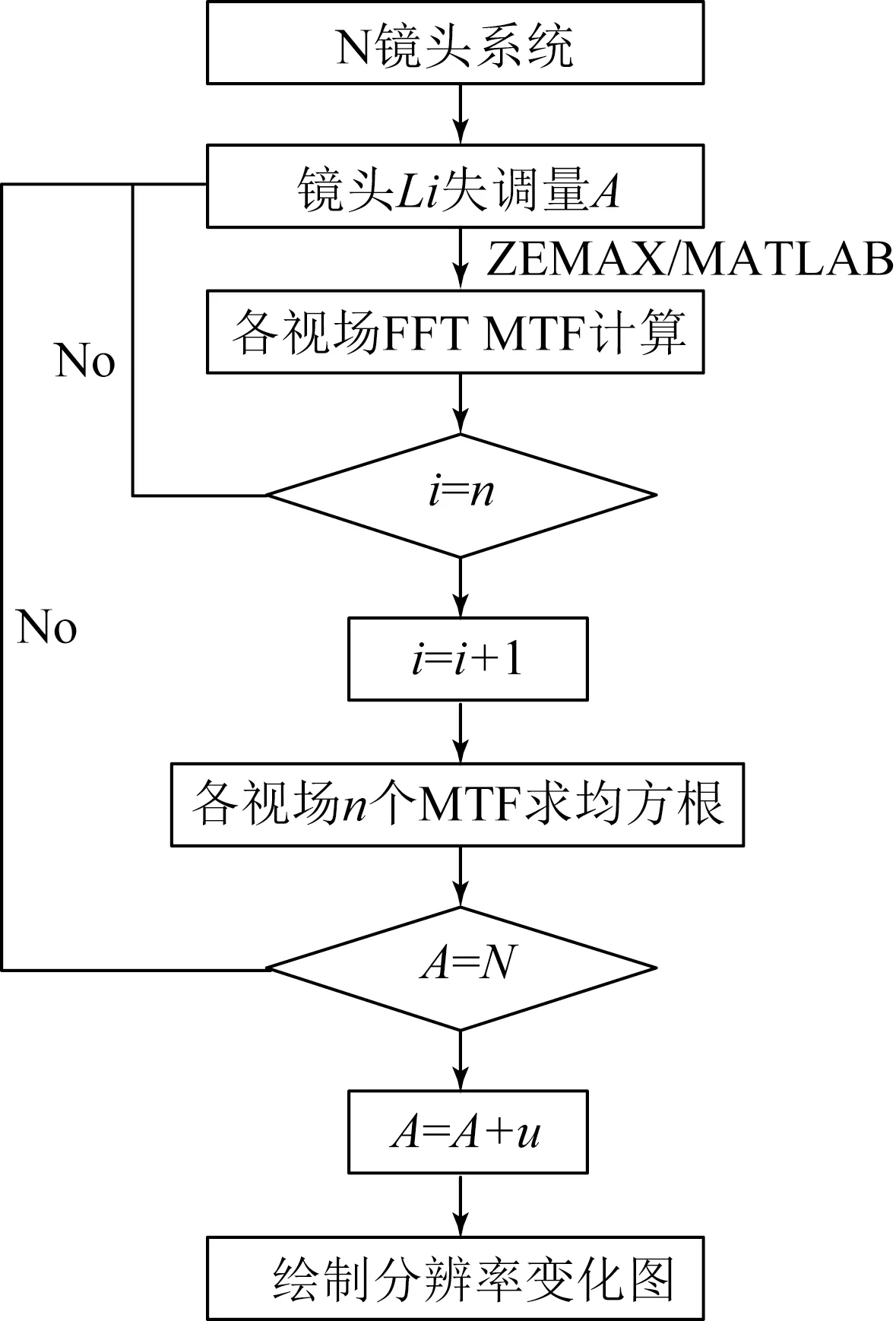
图4　系统分辨率的计算流程图

4　1 μm分辨率的4f系统分辨率影响因素实例分析

本文以非对称型两类高分辨率4f光学系统为例，分析了倾斜、偏心、离轴误差方向对分辨率的影响。

如图5所示，该系统是由9片透镜、1片平板及光阑组合而成的非对称型傅里叶透镜。该系统物高视场为0～±25 mm，工作单波长为0.532 mm。其照片和测试图分别如图6和图7所示。

图5　1 μm高分辨率4f传像系统

图6　1 μm高分辨率4f传像系统实物图

图7　1 μm高分辨率4f传像系统测试图

在没有任何元件加工误差与装调误差时，光学系统的MTF曲线如图8所示。

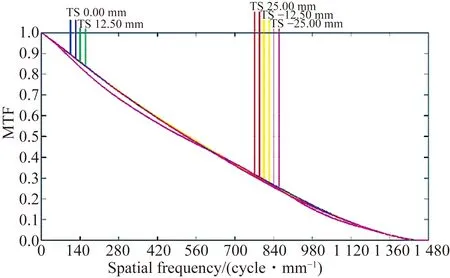
图8　1 μm高分辨率4f系统的MTF曲线图

选取人眼观察最低对比度0.03和对比度0.05观察此时各视场的空间频率，其结果如表2所示。

表21 μm 4f系统在0.03和0.05对比度下的分辨率

Tab.2Resolutions of 1 μm 4fsystem at contrasts of 0.03 and 0.05 respectively

(μm)

本文重点探究了光学面之间的空气间隔、光学面的倾斜与偏心这3种影响因素对分辨率的影响。

该1 μm分辨率4f系统已经在设计公差范围内安装完毕。在公差范围内进行装调误差分析，如倾斜在15″以内，偏心误差在0.02 mm，位移在0.01 mm范围内。

在分析过程中，每一片透镜、平板及光阑产生的倾斜误差从0°开始每增加3″至15″时分辨率的变化规律。首先将透镜L1倾斜3″测得此时系统的分辨率，其次将透镜L2倾斜3″测得系统的分辨率。依次将L3至透镜L9和平板1倾斜3″，通过计算得到在倾斜3″的情况下系统在0.03和0.05对比度条件下5个视场中系统的分辨率。当系统含有3″倾斜误差时，每片透镜倾斜带来的分辨率改变量和系统分辨率的均值如表3所示。图9中坐标轴的横坐标表示每一片透镜的倾斜角度，纵坐标表示系统在透镜倾斜误差产生时分辨率的均方值。

表31 μm 4f系统在对比度为0.03和0.05下含有3″倾斜量的分辨率

Tab.3Resolutions of 1 μm 4fsystem containing 3″ tilt quantity at contrasts of 0.03 and 0.05 respectively

(μm)

续表3

通过该方法一次递增倾斜量至15″，得到系统分辨率和倾斜量的关系曲线，如图9所示。图9中坐标轴的横坐标表示每一片透镜的倾斜角度，纵坐标表示系统在透镜倾斜误差产生时分辨率的均方值。

(a)0.03对比度分辨率变化图

(b)0.05对比度分辨率变化图

由图9(a)和图9(b)可以看出，总体上倾斜使分辨率下降，虽然在极小范围内分辨率有所提高，但总体趋势仍为下降。

在实际装调过程中，装调技术可以保证偏心在0.01 mm以内，因此可以计算所有透镜在0.01 mm以内的分辨率。首先在最大偏心为0.01 mm 时计算 MTF曲线中对比度为0.03及0.05时的空间频率。

根据测量的均值分辨率绘制分辨率与偏心误差的关系，如图10所示。由图10(a)和图10(b)可以看出,偏心会导致分辨率下降。

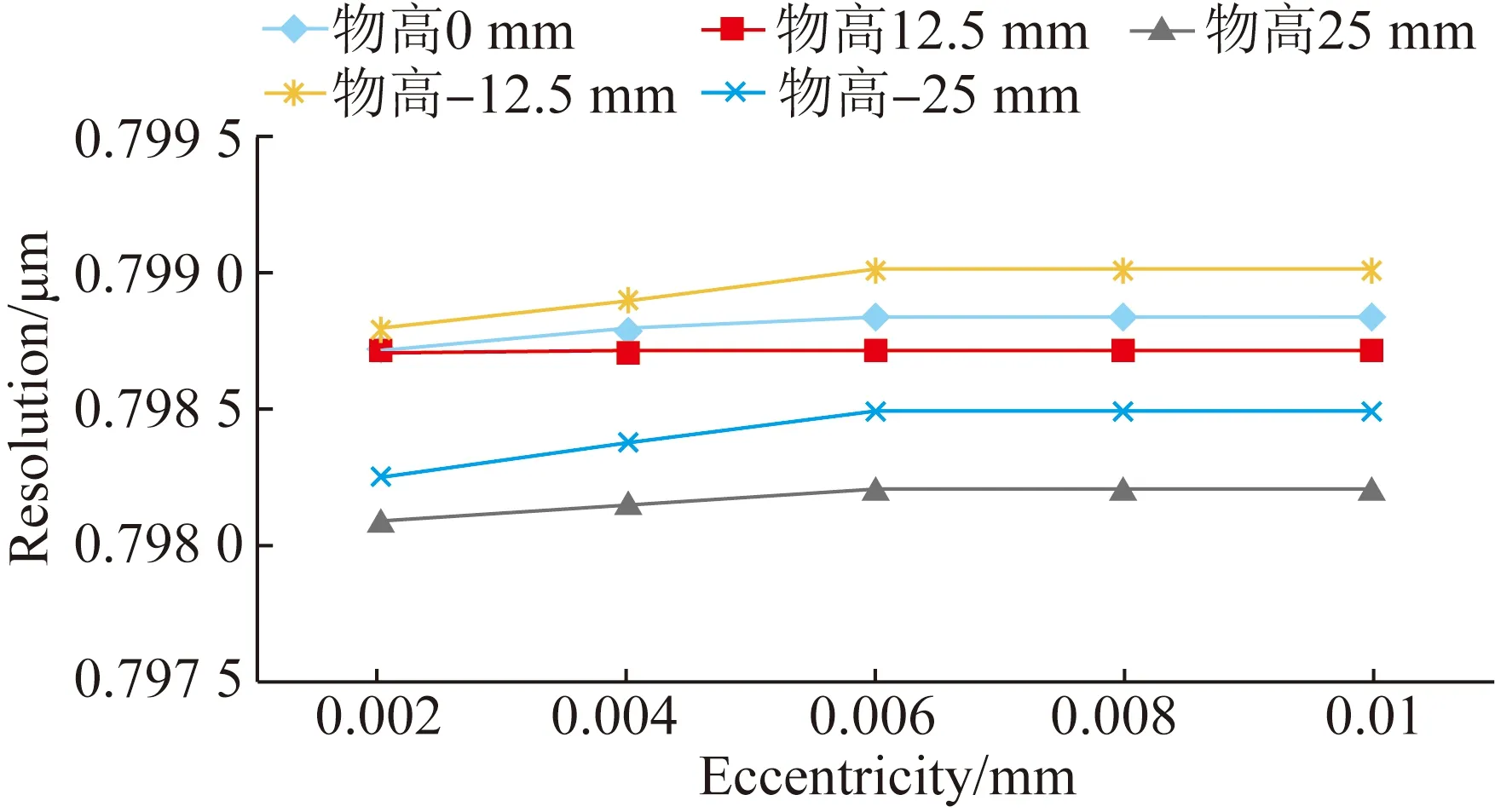
(a)0.03对比度分辨率变化图

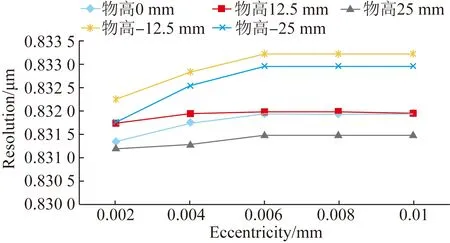
(b)0.05对比度分辨率变化图

(a)0.03对比度分辨率变化图

(b)0.05对比度分辨率变化图

同理，在0.01 mm的间隔位移公差下，根据测量的分辨率均值可以绘制分辨率与位移误差的关系图，如图11所示。由图11(a)和图11(b)可以看出，透镜间隔位移误差会导致视场分辨率的降低，而且非对称型的4f透镜对透镜间隔十分敏感。

5　结　论

本文从加工、装调误差入手，建立了4f光学系统的分辨率影响因素的数学模型，并对非对称型1 μm分辨率的4f光学系统在倾斜、偏心、离轴等误差方面进行分析，在装调公差范围之内，得到了各影响因素与分辨率在0.03对比度和0.05对比度下的关系曲线。结果表明，倾斜、偏心、离轴下降均会导致分辨率的下降。该研究对高分辨率4f系统的装调误差预估其有参考意义[12]。

[1]刘力.傅里叶变换透镜的设计[D]. 重庆：重庆大学，2003.

LIU L.TheDesignoftheFourierTransformLens[D]. Chongqing：Chongqing University， 2003.(in Chinese)

[2]殷蔚.傅里叶变换透镜的设计[D]. 重庆：重庆大学，2009.

YIN W.TheDesignoftheFourierTransformLens[D]. Chongqing： Chongqing University， 2009.(in Chinese)

[3]吕乃光. 傅里叶光学[M].北京：机械工业出版社，2006.

LÜ N G.FourierOptics[M]. Beijing：China Machine Press， 2006.(in Chinese)

[4]李立.光学小波变换的4f系统研究[D]. 重庆：重庆大学，2009.

LI L.Studyonthe4fSystemofOpticalWaveletTransform[D]. Chongqing：Chongqing University， 2009. (in Chinese)

[5]崔龙燮. 4f光学信息处理系统[J]. 华北电力学院学报，1995，22(1)：34-40.

CUI L B.4foptical information processing system [J].JournalofNorthChinaInstituteofElectricPower， 1995， 1.22(1)： 34-40.(in Chinese)

[6]庞志海，樊学武，陈钦芳，等. 失调三反消像散光学系统像差特性[J]. 红外与激光工程，2013，42(3)：653-657.

PANG ZH H， FAN X W， CHEN Q F，etal.. Misalignment induced aberration characteristic of TMA optical system [J].InfraredandLaserEngineering，2013，42(3)：653-657.(in Chinese)

[7]吴晓波，安问斗，杨钢.图像测量系统中的误差分析即提高测量精度的途径[J]. 光学 精密工程，1997，5(1)：133-141.

WU X B， AN W D， YANG G. Error analysing and approaches of improving measuring precision in image measuring system [J].Opt.PrecisionEng.， 1997， 5(1)： 133-141.(in Chinese)

[8]卢智勇，孙建锋，职亚楠，等.直视合成孔径激光成像雷达内发射场波前像差对成像的影响[J].光学学报，2014，34(7)： 0728001-10.

LU ZH Y，SUN J F， ZHI Y N，etal.. Influence of inner wave-front aberration on down-looking synthetic aperture imaging ladar imaging[J].ActaOpticaSinica， 2014，34(7)： 0728001-10.(in Chinese)

[9]于树海， 王建立， 董磊， 等. 基于非均匀周期采样的傅里叶望远镜时域信号采集方法[J]. 中国光学， 2013，6(3)： 395-401.

YU SH H，WANG J L，DONG L，etal.. Time region signal collecting method of Fourier telescopy based on non-uniform periodically sampling[J].ChineseOptics， 2013， 6(3)： 395-401.(in Chinese)

[10]史广维，张新，张建萍，等.几种失调反射光学系统的波像差特性[J]. 红外与激光工程， 2012， 41(1)：160-166.

SHI G W， ZHANG X， ZHANG J P，etal.. Wavefront aberration characteristic of several misaligned reflective optical systems [J].InfraredandLaserEngineering， 2012， 41(1)：160-166.(in Chinese)

[11]朱猛，李翔宇，龙宁波，等.大视场双缝载频散斑干涉成像检测系统[J]. 光学 精密工程，2014，22(1)：13-17.

ZHU M， LI X Y， LONG N B，etal.. Double-slit based carrier frequency speckle interferometric system with large view in field [J].Opt.PrecisionEng.，2014，22(1)：13-17.(in Chinese)

[12]韩亮，田逢春，徐鑫，等.Mallat 算法的光学实现[J]. 光学 精密工程，2008，16(8)：1490-1499.

HAN L，TIAN F CH， XU X，etal.. Optical implementation of Mallat algorithm [J].Opt.PrecisionEng.， 2008，16(8)：1490-1499.(in Chinese)

夏春秋(1991-)，女，山东潍坊人，博士研究生，2008年于中国海洋大学获得学士学位，主要研究方向为光学设计，光学系统的分析。E-mail：chunq.xia@hotmail.com

导师简介：

钟兴(1982-)，男，四川自贡人，研究员，2004年于吉林大学获得学士学位，2009于中科院长春光学精密机械与物理研究所获得博士学位，研究方向为光学仪器的设计与分析。E-mail：ciomper@163.com

(版权所有未经许可不得转载)

Analysis of influence factors of resolution inhigh-resolution 4f imaging system

XIA Chun-qiu1， 2*， ZHONG Xing2，3， LIU Chun-yu2， HAN Pei-xian1，2， JIN Guang2

(1.UniversityofChineseAcademyofSciences，Beijing100049，China；2.ChangchunInstituteofOpticsandFineMechanics，ChineseAcademyofSciences，Changchun130033，China；3.ChangchunSatelliteTechnologyCo.LTD，Changchun130031，China)

*Correspondingauthor，E-mail：chunq.xia@hotmail.com

The factors and its mechanism which influence 4fimaging systemic resolution in practice were studied to guide the design and adjustment of the system. Firstly, the influence of the aberration caused by adjustment error on the system optical transfer function (MTF) in theory, whereby the mathematic model for describing the relationship of them was established. Based on the model, the adjustment error of 4foptical imaging system of 1 μm resolution was derived, and the influence of lens eccentricity, incline and displacement on the MTF was simulated, thus the variations of the resolution with the errors were achieved. The result indicates that within the incline of 15″, the eccentricity error is 0.02 mm and the displacement is within 0.01 mm. The adjustment error results in the decline of the resolution. Although the resolution increases while the incline within a minimum scope, the total trend will not change. The relationship figure of adjustment error and resolution can provide the reference for the error estimation of high-resolution 4fimaging system.

information optics; 4ftransmission system; alignment; mathematical model; curve analysis; high resolution

2015-08-03；

2015-10-06.

中科院青促会专项

1004-924X(2016)07-1573-09

TP391.41；O435.2

Adoi:10.3788/OPE.20162407.1573