学习机会视角下的高中数学概念教学研究

张文宇 常海斌 陈霖

【摘 要】学习机会作为一种特定的课堂教学质量评价指标，为深入分析与改进数学概念教学提供了重要的视角。文章在文献分析的基础上对原学习机会分析框架进行了改进，利用改进后的框架对三节同课异构课的转录文本进行分析，并从学习机会的角度提出教学建议。

【关键词】学习机会；概念教学；课堂教学；函数概念

【作者简介】张文宇，渤海大学数学科学学院教授，硕士生导师，主要从事数学课程与教学论、课程教学与课堂评价研究；常海斌，渤海大学数学科学学院在读硕士研究生，主要从事数学课程与教学论研究；陈霖，渤海大学数学科学学院在读硕士研究生，主要从事数学课程与教学论研究。

【基金项目】辽宁省教育厅一般项目“基于课堂视频分析的小学数学优质课堂特征研究”（WQ2019004）

一、引言

数学概念是反映客观事物在数量关系与空间形式方面的本质属性的思维形式，呈现的是一类对象在数与形方面的内在的、固有的属性［1］。数学中的概念小部分源于对真实事物中的数量关系和空间形式的直接抽象，大部分则是在已有数学理论的基础上经过一系列反思抽象（reflective abstraction）而产生的［2］。这种抽象之上再抽象的特点，使得学生的数学概念学习面临较大的困难。数学概念教学作为数学教学最重要的组成部分，是学生进行数学概念学习的主要方式，高质量的数学概念教学能降低学生的认知负荷，帮助学生建立良好的概念图示。

以评促改是提高数学概念教学质量的重要途径，学习机会作为一种特定的课堂教学质量评价指标，为深入分析与改进数学概念教学提供了一个重要的视角。所谓学习机会是指为促进学生知识的理解过程中，个体的言语及认知思维参与到知识意义建构的可能性［3］20，主要通过深入分析教学重点、课堂时间分配、教师风格、学生言语表现等课堂上发生的各个环节来细化教师教学过程［4］18-24，并以此为依据改善课堂教学。从学习机会的视角对数学概念教学进行研究，可以深入剖析数学概念课的各个环节，为教师的数学概念教学提供参考。

二、研究设计

（一）研究对象及方法

函数是描述客观世界中变量关系和规律最为重要的数学模型。函数概念常常被视为是中学最难学也是最难教的概念之一［5］。因此，本研究选取了三节“函数的概念”同课异构录像课作为研究对象，其中教师T1和教师T3所用的教材为人教A版，教师T2所用的教材为沪教版。

研究采用定性分析与定量分析相结合的研究方法。研究者首先对三位教师的录像课进行初步文字转录，之后结合课堂录像对文字转录进行完善，将修订好的文本上传至MAXQDA软件，依据编码框架对文本进行编码，最后利用MAXQDA和SPSS对编码结果进行量化研究。

（二）分析框架

陈志辉从话语分析的视角开发了学习机会分析框架，用于评估教师在数学概念教学过程中为学生所创设的学习机会。该框架重点关注教学过程中教师的教学语言，但忽视了学生回应这一关键环节。所谓学生回应是指学生通过口头语言的形式表达自己对教师提出的某一数学问题的想法的课堂行为。Duschl和Michaels认为，学生的想法对教师和同伴来说是一种宝贵的资源，而课堂发言为学生提供了一个分享他们的思维和想法、同时了解其他学生思维方式的途径［6-7］，这对于促进课堂公平具有重要意义。此外，作为IRF互动结构中的核心环节，学生回应影响着教师接下来的教学行为，进而也会影响教师赋予学生的学习机会。

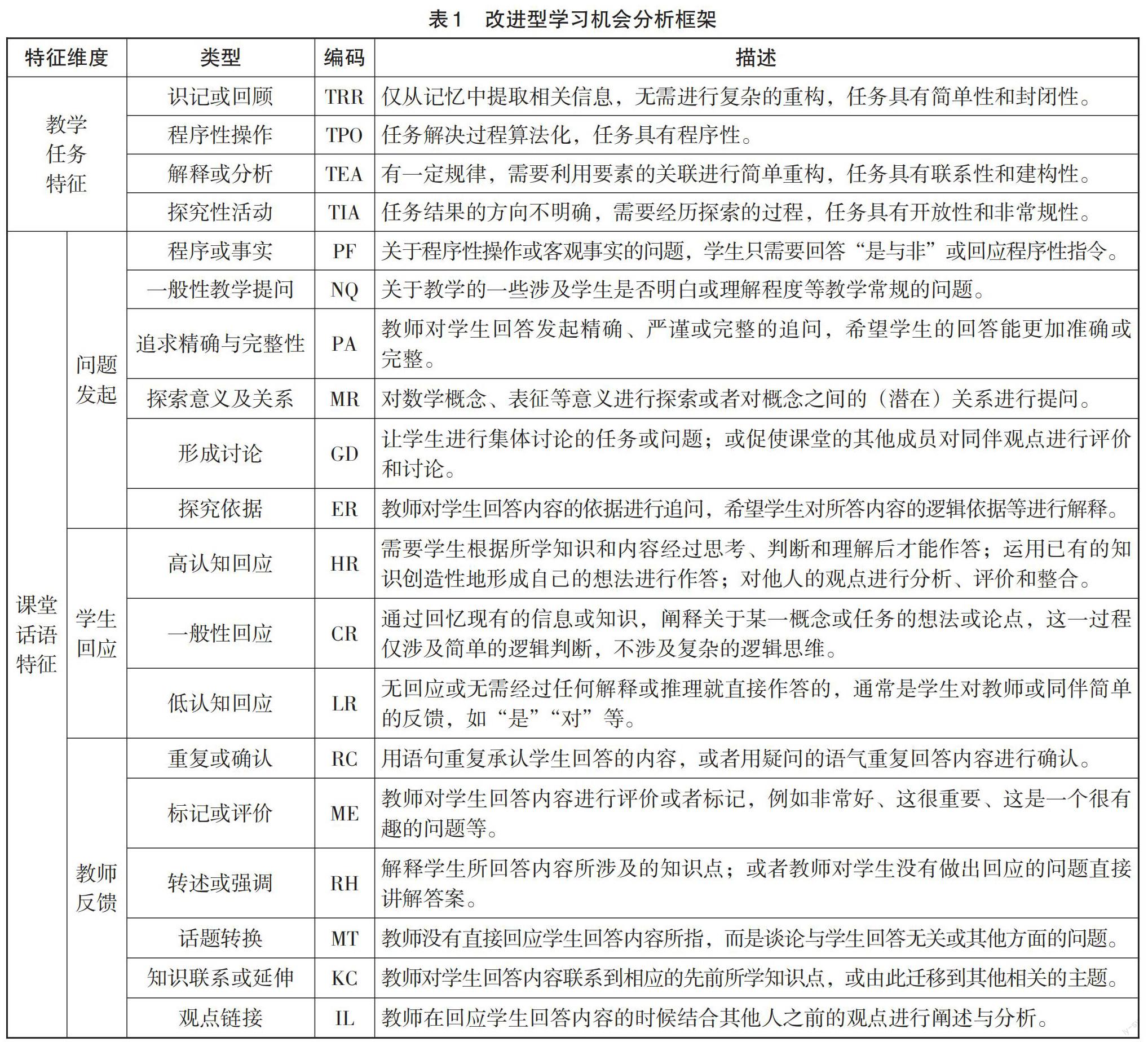
基于此，本研究在原学习机会分析框架中加入了“学生回应”这一子维度，根据Chen等人关于“学生回应”的分类［8］，结合叶立军的研究成果［9］，将学生回应划分为“低认知回应”、“一般性回应”和“高认知回应”三种水平，进而构建了改进型的学习机会分析框架（见表1）。其中探索意义及关系（MR）、形成讨论（GD）、探究依据（ER）、高认知回应（HR）、知识联系或延伸（KC）、观点链接（IL）是学习机会在数学概念教学语境中的六类基本话语内容，即学习机会标准话语类型。在单位互动序列中，学习机会标准话语类型的个数称为学习机会参数（Index of Learning Opportunity，简称ILO），学习机会参数是课堂交流质量的直观体现。

（三）编码流程和方法

本研究首先依据教学任务特征将转录好的文本分为若干个教学任务序列（记为S1、S2……），之后对每一个教学任务序列进行话语结构分析，话语结构分析的主要单位是语步和话轮，如话论1：列车行进的路程S与运行时间T的关系如何表示？该话论包含一个语步，这属于“程序或事实”这一類型的提问，故将其编码为PF；话论2：好，那它是函数吗？该话论包括“好”和“那它是函数吗？”两个语步，其中第一个语步属于“标记与评价”这一类型的教师反馈，故将其编码为ME，第二个语步属于“探索意义及关系”这一类型的提问，故将其编码为MR。

三、研究结果与分析

（一）问题发起与教师反馈方面

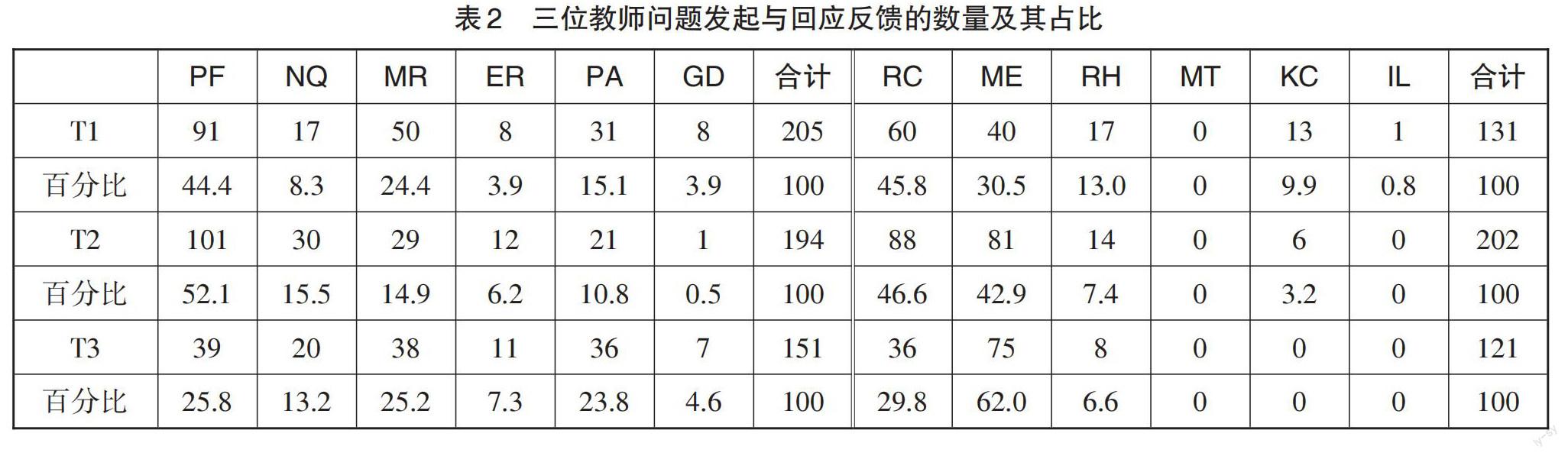
通过对三位教师的课堂录像进行编码分析，结果发现，在问题发起这一环节中，教师T1、T2、T3学习机会标准话语类型的出现次数依次为66次（占比37.1%）、42次（占比26.2%）、56次（占比32.2%）；在回应反馈这一环节中，三位教师学习机会标准话语类型出现的次数依次为14次（占比10.7%）、6次（占比3.2%）和0次（占比0%），三位教师问题发起与回应反馈的具体数量及其占比情况见表2。

由此可见，三位教师更倾向于在问题发起这一环节赋予学生学习机会，而缺乏对学生的应答进行深度分析和评价的意识。通过具体分析，发现以下显著特征：第一，“探索意义及关系”这一提问类型贯穿课堂始终，这对于学生理解数学概念的本质属性具有重要意义；第二，“重复或确认”和“标记或评价”两种反馈类型的结合使课堂互动拖沓冗长，对学生的学习机会造成负向影响。具体分析如下。

1.探索意义及关系：引导学生理解数学概念本质属性的有效路径

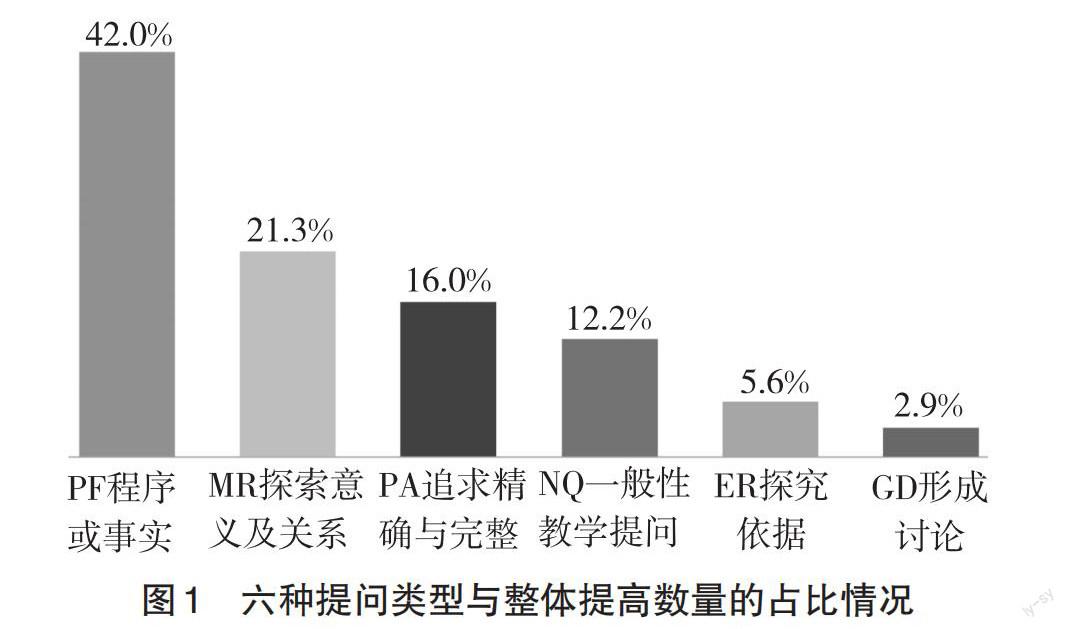
在问题发起方面，教师T1、T2、T3分别在2700 s、2460 s、2760 s内提出了205个、194个、151个问题，平均每13 s、13 s、18 s就提出一个问题。在这些问题中，“程序或事实”这一类型的提问占据总体提问数量的42%（如图1），这类提问多是“是吧？”“是不是？”“对吧？”等程序性问题，教师通常在得到班级集体回答或某一名学生回答后就进入下一个提问。由此可见，三位教师的提问数量偏多、提问频次偏高。研究表明，过于频繁的提问会减少学生的思考时间，干扰学生知识的意义建构，从而影响学生的学习效果［10］。

值得一提的是，“探索意义及关系”这一类型的提问方式贯穿课堂始终。通过分析三位教师的课堂录像及教学设计，发现三位教师在概念引入这一环节都选择了从特殊到一般的处理方式。其中教师T1和教师T3引导学生从“变量说”的角度分析问题，而教师T2则依据沪教版教材的编排顺序，通过引导学生分析幂函数、指数函数和对数函数的共同研究对象来进行概念引入。这两种引入方式都涉及大量的“探索意义及关系”这一类型的提问。在新知讲解环节，三位教师均向学生呈现了解析式、列表和表格三种概念表征方式，让学生深刻体会“对应”这一函数概念的本质属性。在概念辨析环节，三位教师多次询问“它是函数吗？”“它们是同一个函数吗？”等问题，这有助于加深学生对函数概念的理解。在课堂小结这一环节，教师又通过“探索意义及关系”这一类型的提问对初高中函数的概念进行对比，使学生体会从“变量说”到“对应说”的抽象过程，但教师对于这部分内容的处理过于简单，没有深刻阐释引入“对应说”的一般意义。

2.评价+重复：一种冗余的回应反馈模式

回应反馈与问题发起次数之比越大说明教师越关注学生的回应，也说明教师对学生的回复更具体和详细［4］18-24。三位教师回应反馈与问题发起次数的比值依次为0.64、1.04、0.80，可见三位教师对于回应反馈这一环节还不够重视。从三位教师整体的反馈情况来看，ME、RC、RH、KC、IL、MT六种反馈类型的占比情况依次为44.4%、41.7%、8.8%、4.8%、0.2%、0%，“标记与评价”和“重复与确认”这两种类型的回应反馈占比非常高。通过分析代码在同一文件中的位置关系发现，在数学概念教学过程中，这两种类型的反馈通常以“评价+重复”的形式同时出现（如图2），其中线条宽度反映了二者同時被编码的频率，这种教学行为将传统的IRF（启动-回应-反馈）互动结构中的“F”转换为“R+E（评价+重复）”的形式，形成IRRE（Initiation-Response-Repetition-Evaluate）互动结构。研究发现，三位教师在教学过程中都曾使用“R+E”形式打断学生回应的行为，导致学生不能完整、流畅的进行数学表达。从学习机会的视角来看，这种互动结构是拖沓的，对学生的学习机会并无积极意义，甚至干扰学生的思考过程，对学生的数学概念学习造成负面影响。

（二）学生回应方面：以“低认知回应”和“一般性回应”为主的现实困境

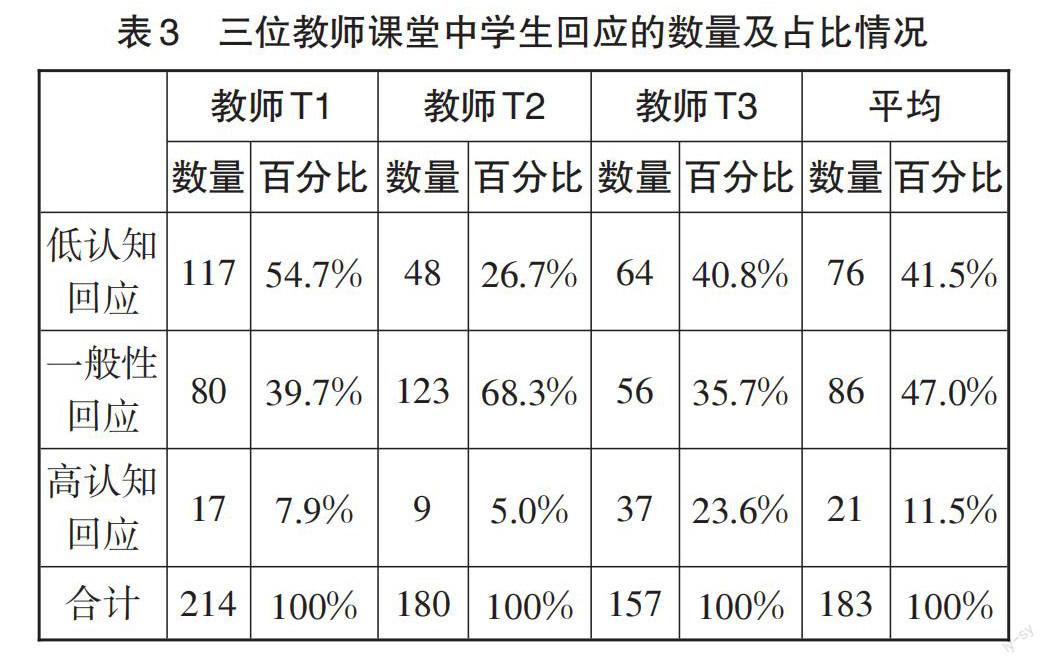
在教师T1、T2、T3的课堂中，学生回应这一环节学习机会标准话语类型出现的次数依次为17次（占比7.9%）、9次（占比5%）、37次（占比23.6%），仅占总回应数量的11.5%；而低认知回应和一般性回应则分别占回应总量的41.5%和47.0%，三位教师课堂中学生回应的数量及占比情况见表3。通过对课堂录像分析发现，在数学概念教学过程中，低认知回应主要以集体回应为主，如“嗯”“是”“对”等程序性回答，学生无须经过任何的解释和推理即可作答。从教学连贯性的角度来看，这类回应有利于课堂教学持续高效的推进，但也会造成一些学生“随大流”和“随意应答”的现象，难以保证学生的学习机会。一般性回复，如“初中函数的概念就是y等于一个关于x的式子；我觉得y随着x的变化而变化了”，这类回复仅需通过回忆已有知识或经过简单的逻辑判断即可作答，无须进行复杂的思考与重构。基于以上分析可以发现，在实际课堂中学生的回应水平整体偏低，主要以“低认知回应”和“一般性回应”为主，一些学生的言语表述不准确、不连贯，这很容易造成学生函数概念理解不清晰、不透彻，学生的数学语言表达能力有待提高。此外，双变量Pearson检验结果显示，教学任务特征与高认知回应呈弱正相关（r=0.351，P＜0.01），这表明高认知要求的数学任务与学生的高认知回应之间并无必然联系。

（三）教学任务设置方面：以高认知水平期望为主的任务类型失衡

教学任务类型的设置与安排体现了教师对学生认知水平要求的期望，教师T1、T2、T3分别在课堂中设置了29个、32个、32个不同认知要求的数学任务。具体来讲，对于“识记与回顾”“程序性操作”“解释与分析”“探究性活动”四种类型的数学教学任务，教师T1在课堂中设置的数量依次为7个（占比24.1%）、0个、22个（占比75.9%）、0个，教师T2在课堂中设置的数量依次为11个（占比34.1%）、0个、21个（占比65.5%）、0个，教师T3在课堂中设置的数量依次为2个（占比6.3%）、0个、27个（占比84.4%）、3个（占比9.4%）。可见，几位教师教学任务类型的设置失衡，主要以“解释与分析”为主，另外几类数学任务整体占比较少。这类任务具有一定的复杂性和联系性，说明几位教师对学生的认知水平要求的期望较高。

此外，双变量Pearson检验结果显示，教学任务特征与ILO之间无统计学意义（r=0.295，P＜0.01），这表明高认知要求的数学任务与学生所获的学习机会之间无必然联系。研究还发现，在三位教师的课堂中，随任务序列的推进，学习机会参数的变化幅度较大，这说明教师赋予学生的学习机会在整个课堂中是不均衡的，有进一步提升和完善的空间。

四、研究结论与教学建议

（一）研究结论

第一，教师在问题发起环节赋予学生的学习机会较多，“探索意义及关系”这一类型的提问对于数学概念教学具有重要作用。但教师提问数量偏多、提问频率偏高，对学生的学习机会造成不良影响。第二，在学生回应方面，学生在课堂中的整体回应水平较低，问题回答不严谨、不完善，数学语言表达能力有待提高，学生在这一环节中获得的学习机会较少。第三，教师在回应反馈环节赋予学生的学习机会非常少，“重复或确认”和“标记与评价”两种反馈类型占比过高，导致课堂互动结构拖沓冗长。此外，教师多次利用“R+E”的反馈模式打断学生发言，这种不良的教学行为需进一步改进。第四，在教学任务特征方面，教师教学任务的设置类型单一，且对学生的数学认知水平期望较高，随教学任务序列的推进，学习机会参数的变化幅度较大。

（二）教学建议

1.以“探索意义及关系”为中心，构建多元化的课堂提问模式

课堂提问是课堂交流的起点，对课堂教学有着重要的驱动意义［11］，学习机会视角下的数学概念教学倡导以“探索意义及关系”为中心的多元化提问模式。所谓“探索意义及关系”就是不断对数学概念、表征等意义进行探索或者对概念之间的（潜在）关系进行提问［3］139，通过这一提问方式让学生经历概念引入、概念生成、概念辨析和概念应用的过程，从而使学生在头脑中形成概念表象，建立良好的概念图示。例如以下问题：下面两组函数是同一函数吗？①y=x；y=（x2）[1/2]；②y=sin2x+cos2x，x[∈]（-[∞]，+[∞]）；y=1，x[∈]（-[∞]，+[∞]）。教师提出问题后，无论学生回答“是”还是“不是”，教师都可以利用“探索依据”这一类型的提问方式追问原因。如果学生彼此之间意见不统一，教师还可以利用“形成讨论”这一类型的提问方式组织学生进行小组讨论或对他人的回答发表看法，而在讨论上述函数定义域的过程中，又可以利用“探索意义及关系”对二次根式和三角函数的相关内容进行提问。此外，教师还可以从图象的角度入手，让学生体会函数的多元表征方式。这种以“探索意义及关系”为中心的多元化课堂提问模式，可以使课堂提问类型由单一化走向多元化，由“高数量”转向“高质量”，从而在数学概念教学过程中赋予学生更多的学习机会。

2.正确认识教师反馈的重要意义，增加教师反馈环节的学习机会

教师在教师反馈这一环节赋予学生的学习机会少，且反馈类型单一、反馈结构拖沓冗长，究其原因是教师没有对反馈这一环节的教育价值形成正确的认识。学习机会视角下的数学概念教学倡导利用“知识联系与延伸”和“观点链接”两种类型的教师反馈来对学生的回應进行应答。首先，教师可以利用“知识联系与延伸”引导学生回顾已有知识经验，帮助新概念找到知识的固着点。例如，在“函数的概念”的教学过程中，教师可以带领学生在课堂小结部分对“变量说”和“对应说”进行分析和比较，让学生在“变量说”的基础上，体会函数概念的抽象过程及其意义。其次，教师可以利用“观点链接”这一类型的反馈方式，引导学生对其他同学的观点进行分析与评价，以此来实现新话轮的构建，这对于促进课堂的多向交流具有重要意义。最后，教师要优化自己反馈结构，避免过多“R+E”形式的反馈，要保证反馈语言的简洁性、反馈时机的恰当性以及反馈内容的有效性［12］，用更简洁和更有针对性的反馈提高学生在概念学习中的学习机会。

3.以学生的数学认知结构水平为依据，合理设置数学概念教学任务

研究表明，数学任务特征与学生所获得的学习机会之间无必然联系，一味地追求高认知水平的数学任务不仅不会提高学生的学习机会，反而会使学生对数学概念学习产生习得性无力感，失去对数学学习的兴趣。因此，教师在教学过程中要以学生的数学认知结构水平为依据，结合授课班级的学情，从整体和部分两个角度有针对性地设置数学概念教学任务。对于学生数学认知能力较强、数学基本知识和基本技能掌握较好的班级，教师可以设置一些结果方向不明确的开放性任务。对于数学基础一般的班级学生，教师应设置以简单的、封闭的程序性的任务为主，帮助学生夯实基础，增强学习数学的信心。但是，教师对班级中数学认知结构水平较高的学生也应给予特定的学习机会，以保证教学过程的公平。此外，教师还要进一步均衡课堂中学习机会的分布，以保证学生在一节课的大部分时间内都处于较高水平的思维状态。

4.以数学概念教学为切入点，提升学生的数学语言表达能力

在三位教师的课堂中，学生回应水平偏低、数学语言表达不完整、不严谨，教师应在概念教学中有意识的培养学生数学语言表达能力。首先，在概念生成的过程中，教师要鼓励学生自行分析总结、互动交流，让学生自己给概念下定义，这不仅有利于培养学生的数学语言表达能力，而且还能帮助学生形成严谨的思维和理性的精神。其次，教师要进一步加强概念辨析环节的教学，要保证学生的概念学习是有意义的学习，而不是机械的死记硬背，很多学生数学表述不规范，就是因为对数学概念理解得不透彻。例如“二面角”和“二面角的平面角”，前者是一个空间图形，而后者是一个由两条射线组成的平面图形。在实际教学过程中，学生经常将“二面角的平面角为60°”错误的表述为“二面角为60°”，这说明学生没有真正理解二面角的概念。再次，教师要注重对学生进行数学语言的语义转换训练。例如，函数具有解析式、图象和表格三种表征形式，教师可以引导学生利用不同表征形式对函数的概念进行阐述和理解，赋予学生更多的表达机会。最后，教师可以通过构建概念系与概念域，指导学生对已有知识之间的关系进行分析和总结，这样不仅能强化学生的概念理解，使学生的知识体系更加系统，而且对于培养学生的数学语言表达能力也具有重要意义。

参考文献：

［1］曹才翰，章建跃.数学教育心理学［M］.北京：北京师范大学出版社，2015.

［2］SIMON M A .Explicating mathematical concept and mathematicalconception as theoretical constructs for mathematics education research［J］.Educational Studies in Mathematics，2016（9）：117-137.

［3］陈志辉.学习机会视角下初中数学概念教学的实证研究［D］.上海：华东师范大学，2018.

［4］辛涛，姜宇，王旭冉.從教育机会到学习机会：教育公平的微观视域［J］.清华大学教育研究，2018（2）：18-24.

［5］史宁中，濮安山.中学数学课程与教学中的函数及其思想：数学教育热点问题系列访谈录之三［J］.课程∙教材∙教法，2007（4）：36-40.

［6］EDMONDSON E，CHOUDRY F. Talking the talk：Exploring teacher learning and their use of discourse strategies［J］.School Science and Mathematics，2018（11）：273-289.

［7］MICHAELS S ，C O’Connor，RESNICK L B. Deliberative discourse idealized and realized：accountable talk in the classroom and in civic life［J］.Studies in Philosophy & Education，2007（4）：283-297.

［8］CHEN Y C，HAND B，Norton-Meier L. Teacher roles of questioning in early elementary science classrooms：a framework promoting student cognitive complexities in argumentation［J］. Research in Science Education，2017（2）：373-405.

［9］叶立军，郑欣.专家型数学教师代数复习课提问行为研究：以一次函数和反比例函数为例［J］.数学教育学报，2018（2）：46-49.

［10］胡启宙，孙庆括.初中数学教师课堂提问的方式和反馈水平实证研究：基于三位教师课堂录像的编码分析［J］.数学教育学报，2015（4）：72-75.

［11］刘晨艳.课堂提问的结构化：内涵、价值与策略［J］.教育理论与实践，2021（11）：54-57.

［12］李秀梅，李如密.教师教学反馈语：再识、透视与审思：以小学语文课堂为例［J］.上海教育科研，2020（2）：63-67.

（责任编辑：陆顺演）