GNSS 直接位置估计技术综述

周志健，冉承新，戴志强，陈正坤，徐奕禹，朱祥维

(中山大学电子与通信工程学院,广东 深圳 518107)

0 引言

全球导航卫星系统(GNSS)能够在全球范围内为用户提供连续实时的空间位置信息，具有覆盖广、高精度、全天候等突出优点，在民用领域、军用领域都得到了广泛应用.随着卫星导航应用的不断拓展，导航接收机也面临越来越多复杂的工作环境，这对导航信号接收技术是一个严峻的挑战.

在导航接收机端，目前所采用的大多数是标量接收机，即标量跟踪环路的接收机[1]，其结构如图1 所示.在标量接收机中，通过每个通道跟踪一颗卫星，各个通道之间不存在信息交流.每个通道内的鉴别器分别计算出伪码相位误差和载波相位误差后，经过环路滤波器直接反馈给本通道的载波/码数控震荡器(NCO)，NCO 调节本地伪码和载波的频率，使本地复制信号的码相位、载波频率与接收信号中的码相位、载波频率一致，从而完全剥离接收信号中的伪码和载波，解扩出导航数据.这种结构简单，易于实现，但是存在以下缺点：

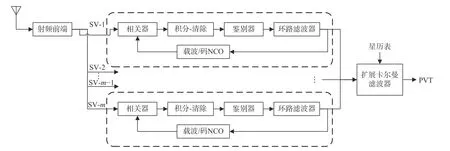
图1 标量接收机结构

1)跟踪灵敏度和动态性能较差[2-3].在弱信号环境或者高动态场景下，跟踪环路的跟踪误差会急剧增大，从而不能保持对卫星信号的稳定跟踪，最终无法进行导航定位解算.

2)跟踪连续性和信号可用性较差.标量跟踪环路对已经失锁或暂时遮挡的导航信号的误差估计会发散，不能保持在一个较小的范围之内[4]，因此当遮挡结束后，卫星信号强度恢复正常，标量跟踪需要重新捕获.

3)抗干扰性能较差.在标量跟踪环路中，各跟踪通道相互独立，当某个通道受到干扰的影响时，环路跟踪误差增大[5]，而其他通道也无法对其进行辅助跟踪，最终导致失锁.

针对以上三个缺点，矢量接收机在结构上做出了一些改进，如图2 所示，各通道的载波/码NCO 的控制变量不再由各自的环路滤波器提供，而是由导航滤波器统一生成.矢量接收机不但将各通道关联起来，而且还将跟踪和导航解算融合在一起，实现了多通道信号的联合处理.这使得矢量接收机在跟踪灵敏度、动态性能、抗干扰性能等方面都得到一定的提升，且对于信号遮挡场景也不用重新进行捕获[6-7].

图2 矢量接收机结构

但矢量跟踪也存在一些不足之处，主要包括：1)矢量跟踪算法对码相位的估计本身是有偏的，其收敛点不唯一且不为零[8]；2)由于通道间的相互耦合，当一个通道出现误差时，对其他通道也会造成影响；3)矢量跟踪环路的计算量非常大，其实现成本高.

矢量跟踪虽然一定程度上改善了标量跟踪的缺点，但究其本质仍属于两步法的范畴，是基于“伪距域”的处理策略，即接收机解算自身位置时需要先获取伪距信息，无法达到最大似然估计(MLE)下的最优解.而直接位置估计(DPE)是通过联合所有可见卫星信号直接在导航域进行信号能量积累，并利用联合积累输出通过一步估计得到导航解，如图3 所示.无需捕获跟踪就能利用所有可见卫星信号，在弱信号环境下依然能保持较好的定位性能[9]，且灵敏度较高.由于DPE 是通过多个通道的联合积累结果来估计导航解，所以当部分通道受到多径干扰时仍能保持较好的定位精度[10].最后，DPE 是在导航域内通过一步估计得到导航解，是基于“导航域”的处理策略，属于一步法.Closas 等[11]证明了在MLE 下，DPE 方法才是最优的.

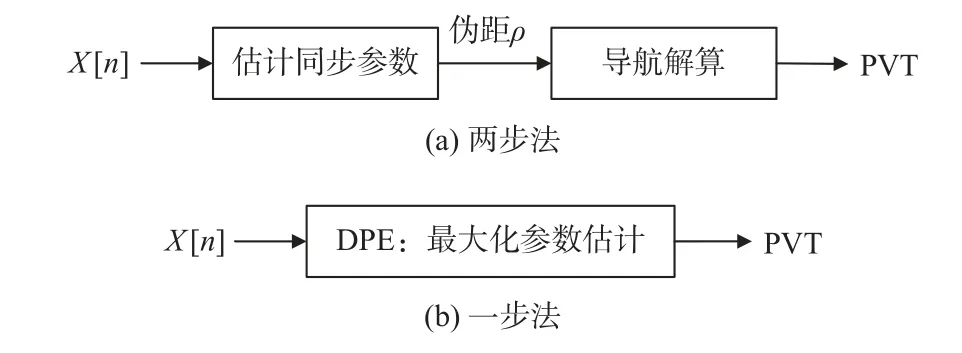
图3 导航信号估计方法示意图

1 DPE 技术研究进展

DPE 作为导航领域的一项新兴技术，能够克服传统方法在高楼矗立的城市、室内等复杂环境下无法正常工作的缺点，因此越来越多的学者投入到DPE 的研究当中.下面先对DPE 的基本原理进行介绍，然后分别从理论、实现和应用三个层面分析DPE 技术的研究进展，最后进行总结.

1.1 基本原理

早在2007 年，Closas 等[9]就推导得到了GNSS框架中位置的MLE 量，即DPE，因此这篇文献也被认为是提出DPE 概念并从原理上进行推导的开篇之作.下面，对DPE 的主要推导过程进行简要介绍.

考虑接收机天线接收了K个快拍，那么接收信号模型可以写成

式中：x∈C1×K是接收机的观测矢量；a=[a1,a2,···,aM]∈C1×M是M个接收卫星信号的幅度，D(θ)=[d(t0),d(t1),···,d(tK-1)]∈CM×K是基函数矩阵；d(t)=[d1,d2,dM]T∈CM×1，分量，τ为码相位，fd为载波多普勒频移；n∈C1×K是零均值加性高斯白噪声，方差为.

考虑到MLE 等效于在零均值加性高斯白噪声的假设下通过最小二乘获得的解，所以最大化观测的似然函数等效于最小化

且存在以下互相关定义：

于是可以直接得到MLE 的幅度

将式(4)代进式(2)中，即可得到

已知卫星星历，码相位和载波多普勒可以根据接收机的位置、速度以及钟差和钟漂求出：

式中：ρi为接收机和第i颗卫星的伪距；c为光速；δt和δti为接收机和第i颗卫星的钟差；fdi为多普勒频率；v和vi分别代表接收机和第i颗卫星的三维速度；ui为接收机和第i颗卫星的方向矢量，ε为测量误差；fc为载波频率；p=(x,y,z)和pi=(xi,yi,zi)为接收机和第i颗卫星的三维位置坐标..

至此，从传统的基于同步参数的定位转变为了基于接收机状态的DPE 定位.

1.2 理论层面

DPE 是基于导航域的一步估计法，被证明是最大似然准则下的最优估计，因此理论上DPE 也会拥有比传统两步法更出色的性能.下面主要从弱信号环境、多径干扰与动态环境、压制干扰和欺骗干扰这三个方面对DPE 的性能与传统两步法(标量跟踪或矢量跟踪)进行比较分析.

1.2.1 弱信号环境

对弱信号的鲁棒性是DPE 最为出色的优点，围绕此特点前人做了许多研究.Closas 等[9,11]从最大似然出发，推导得到DPE 后，继续从数学上证明了传统两步法定位误差的协方差不能小于DPE 方法的协方差，即在均方误差意义上，传统两步法的估计性能只能低于或等于DPE 方法给出的性能.并且通过仿真验证了在弱信号环境下，DPE 方法的定位误差要低于传统两步法.

在真实信号场景下，Lin 等[12]对比分析了DPE和矢量跟踪(集中式)在室内的定位误差.实验结果表明，在长相干积分时间的前提下，两者拥有相似的性能.但是随着相干积分时间的减少，矢量跟踪的定位误差大幅增加，但是DPE 依然保持较好的定位性能，再次证明了DPE 更加适用于室内等弱信号环境.陈万通等[13]也基于真实信号，通过实验证明，对未能成功捕获的卫星弱信号依然可有效参与到定位解算中，进一步证明了DPE 对弱信号的鲁棒性.

上述研究虽然论证了DPE 方法针对弱信号环境的性能优势，但是却没有给出相应的理论极限.文献[10]中推导了传统两步法和DPE 方法的克拉美罗下界，证明了DPE 方法的克拉美罗下界小于等于传统两步法，只有在高信噪比和弱多径干扰的理想情况下两者才具有相似的性能.假设除了一颗卫星之外的所有卫星具有相同的载噪比45 dB-Hz，然后在一定范围内改变这一颗卫星的载噪比得到克拉美罗下界，如图4 所示，其中M代表卫星数，N代表阵列天线数.

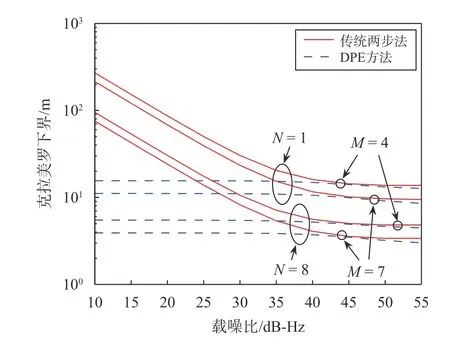
图4 克拉美罗下界和信噪比的关系[10]

但是克拉美罗下界作为评价估计器性能好坏的一个常用指标，仅在高信噪比区域内才比较准确，在较低的信噪比区域会产生高估计误差.因此，使用克拉美罗下界不利于探讨分析DPE 方法和传统两步法在弱信号场景下的性能极限.于是，Gusi-Amigo 等[14]推导了加性高斯白噪声信道下DPE 方法和传统两步法的Ziv-Zakai Bound(ZZB)，并指出对于具有不同信噪比的场景，从克拉美罗下界获得的传统加权矩阵对于整个信噪比范围不是最优的，而从ZZB获得的加权矩阵拥有更好的性能.

1.2.2 多径干扰与动态环境

在城市环境中使用GNSS 进行导航定位主要面临三个挑战：信号衰减、多径干扰和动态环境.关于DPE 在信号衰减场景(即弱信号环境)下的性能表现已经在上一节进行讨论，下面主要对多径干扰和动态环境进行分析.

Closas 等[10]除了推导传统两步法和DPE 方法的克拉美罗下界以外，还通过仿真实验证明了相对于传统两步法，DPE 方法拥有更出色的抗多径性能，并指明此性能的改进是来源于DPE 联合处理所有卫星信号的结构体制.更进一步地，Closas 等[15]讨论了在受控的统计通道模型(CSCM)和陆地移动多径信道模型(LMMC)下评估多径干扰对DPE 性能的影响和敏感性，分别在衰落、多径和用户动态这几种信道条件下，对DPE 和DLL 进行比较，证明了DPE 的优越性.

上述研究是基于单一的信道条件，例如考虑信号衰落时就不考虑多径和动态，这种设置虽然有利于探讨DPE 在某一方面的性能优势，但与现实信号环境不太符合.在真实的城市环境中，当GNSS 信号较弱且车辆在移动时，多径对跟踪定位性能的影响较小，信号衰减和用户动态起主要作用；当GNSS 信号强，定位误差则主要取决于多径，尤其是在车辆静止时.Liu 等[16]分别在无多径的动态弱信号环境和强信号的多径干扰环境下进行仿真实验，比较分析了直接位置跟踪环路(DPTL)和联合矢量跟踪环路(JVPTL)的性能.实验结果表明：两种测试环境下，DPTL 的定位误差均优于JVPTL.此处主要对高动态性能进行分析，在0.1～2 g 的加速度范围内，两者的跟踪阈值相同，但DPTL 的定位误差都要小于JVPTL.在2～5 g的加速度范围内，DPTL 的定位误差开始大于JVPTL，需要注意的是此时JVPTL 的跟踪阈值也要大于DPTL，说明JVPTL 更小的定位误差是牺牲了跟踪阈值换来的.

1.2.3 压制干扰与欺骗干扰

对弱信号的鲁棒性及出色的抗多径性能是DPE比较直观的优势，除此之外，国外学者还研究了DPE在抗干扰和防欺骗上的性能.Ng 等[17-18]利用基于PyGNSS 的DPE 接收机架构来评估相较于传统标量跟踪，DPE 和直接时间估计(DTE)应对干扰和欺骗的能力，结果表明DPE 和DTE 在干扰和欺骗存在的情况下依然能输出稳定可靠的位置和时间测量结果.文中所采取的干扰皆为压制干扰，不断增加噪声功率，DPE 保持鲁棒性，而标量跟踪的跟踪误差增大，性能下降.文中所采取的欺骗则比较简单，其中文献[17]所使用的欺骗信号是从原始信号约2 km 之外的接收机收集的.文献[18]所使用的欺骗信号是原始真实信号延迟180 m(即0.6µs)得到的.这两种欺骗信号都无法落在DPE 和DTE 的主瓣上，因此无法成功欺骗DPE 和DTE.此时，欺骗信号由于其大功率特点，对真实信号就相当于干扰的作用.

除了研究DPE 在压制干扰和欺骗干扰下的性能表现，还可以利用多个DPE 接收机反向定位欺骗源的位置.Xie 等[19]提出了一种解扩直接位置确定算法(DS-DPD)，该算法先建立接收信号模型，然后利用最大似然准则来构建DS-DPD 的目标函数，最后通过目标函数的二维谱搜索获得欺骗者的位置参数.由于充分利用了时延、多普勒频移、DOA 和码序列信息，定位精度可提高十倍以上.

1.2.4 小结

DPE 的优势性能、是否进行仿真测试和真实场景测试以及最终得出的结论总结如表1 所示.

表1 DPE 性能研究状况

DPE 本身的结构决定了其对弱信号有天然的鲁棒性，这也是DPE 最突出的优势.因此，关于DPE 在弱信号环境下的性能研究比较深入，其理论极限也比较清晰.关于多径和动态场景下的研究目前还只在仿真信号下测试过，后续可以考虑在真实信号场景下进行测试和优化.而压制干扰和欺骗干扰是可信导航领域的重点，目前关于DPE 在这一领域的研究较少，针对生成式欺骗的DPE 研究仍是空白.因此关于DPE 在欺骗干扰方面的研究可以继续拓宽、拓深.

1.3 实现层面

除了对DPE 本身性能的探讨分析，国内外学者对DPE 的实现也做了许多研究.主要可以概括为两部分，分别是优化算法提高计算效率和优化模型提高定位精度，下面分别对这两方面进行分析.

1.3.1 计算效率

由于DPE 优化函数的高维性和非线性，其计算量十分庞大，且在计算上缺乏有效的优化算法.Closas等[20]研究了空间交替广义期望最大化(SAGE)算法，该方法以迭代逼近DPE 的估计结果，从而大大降低了问题的复杂程度.但是仿真结果表明SAGE 算法对初始化很敏感，对于正确的初始估计，SAGE 算法认为达到了克拉美罗下界.

除了在算法上进行优化，还可以对DPE 进行改进，在其他性能上做出轻微的牺牲来换取计算量的大幅下降也是可行之道.Daniel 等[21]提出了一种松弛DPE 方法，主要是通过利用可用的几何关系来保留DPE 的优点并降低其计算量，并且对定位精度的损失最小.而Ng 等[22]另辟蹊径，通过低占空比提高DPE 的计算效率(低占空比指的是执行测量更新的次数少，时间更新的次数多，因为前者计算量大，后者计算量小).静态实验证明占空比低至2%的DPE 和连续DPE 拥有相似的性能，动态实验证明占空比低至2%的DPE 仍能成功跟踪车辆，其精度要优于信号衰减下的连续矢量跟踪.此外，针对两步法容易实现但不是最优解、DPE 是最优解但计算量太大的特点，Vincent 等[23]提出了介于两者之间的加权最小二乘(WLS)最小化的两步过程，显示为渐进等效于ML.

在DPE 中，滤波器的选取也尤为重要，Closas等[24]研究了在DPE 中使用贝叶斯滤波器，提出了SIRPF(sampling importance resampling Particle filter)算法和SCKF(square root cubature Kalman filter)算法，并在现实场景下使用计算机模拟进行了性能比较.结果表明，在相同数量的生成粒子下，SCKF 算法优于SIRPF 算法.

1.3.2 定位精度

在实现层面上除了优化算法以提高计算效率的相关研究，同时还需要考虑提高定位精度的需求.Dampf 等[25-27]进一步围绕DPE 和粒子滤波结合做了一些工作：1)首次在商业软件上实现，并用实验证明，在多径占主导的城市峡谷环境BDPE(bayesian direct position estimation)的表现要比标量跟踪要好，但稍逊于矢量跟踪.在桥梁、隧道等弱信号或信号拒止环境中，BDPE 的性能要远远优于矢量跟踪和标量跟踪[25]；2)推导了最优粒子权重，提供了一种在对数尺度上执行权重更新的解决方案，以克服数字计算的有限精度问题[26]；3)讨论了最佳但最简单的测量更新的问题，并通过引入用于距离测量的干扰参数来解决剩余用户距离误差(如卫星轨道和时钟钟差、电离层和对流层误差)，扩展了现有框架[27].

针对DPE 应用在复杂环境下的特点，李伟鹏等[28]提出了加权DPE 来提高复杂环境下DPE 的性能，对不同质量卫星信号的相关值加权后再相加，并通过仿真数据和实测数据进行实验，采用不同的加权模型均能改善DPE 的联合积累输出性能和导航性能，提高了导航解精度.

除了对模型进行优化以外，对模型的误差进行分析、将误差来源研究清楚也是一项较为重要的工作，可以为后续提高定位精度指明方向.Peretic[29]研究了使用采样信号求解DPE 方程和解方程所引入的近似对定位精度的影响，此外还使用CUDA C/C++语言开发了一个并行处理的DPE 软件接收机，并在NVIDIA Jetson TX2 portable GPU 上进行实现，大大提高了DPE 算法的解算速度.

关于DPE 的主要理论结果、架构以及改进都在文献[30]中进行了分析，特别地，文中还总结了DPE在实现方面几个未解决的问题，最后用合成数据进行实验，探讨了DPE 在定位精度、可靠性和可用性上的优势.

1.3.3 小结

总结DPE 实现层面的研究方向、研究内容以及研究结果，如表2 所示.DPE 是通过联合所有可见卫星信号直接在导航域进行信号能量积累，并利用联合积累输出通过一步估计得到导航解.从结构上已经决定了DPE 的计算量是十分庞大的，这对于达到实时定位的要求是一个严峻的挑战，也成了制约DPE 广泛应用的重要原因.因此，如何优化算法以提高计算效率将会是今后DPE 相关研究的一个重点方向.在硬件层次可以使用GPU 来实现DPE；在算法层面可以考虑优化DPE 的模型，比如文献[29]中通过流形解耦将DPE 这个八维优化问题分解为两个四维优化问题，然后分别进行求解，其计算量大大减少.此外，在理论上DPE 是最大似然准则下位置的最优估计，能获得高于传统两步法的定位性能.但目前的研究仍缺乏对DPE 定位精度的探讨和分析，所以深入挖掘DPE 定位精度的极限也尤为重要.

表2 DPE 实现研究状况

1.4 应用层面

针对城市导航中非视距信号(NLoS)导致GNSS信号可用性降低的问题，进行了一些研究.文献[31]提出利用DPE 方法来处理NLoS 信号，并通过实验证明DPE 方法的水平定位误差比传统标量跟踪方法减少了40 m.文献[32]将DPE 和图像地图匹配进行深度集成，使用已知位置作为先验信息，缩减估计参数获得冗余，提高关键基础设施的防欺骗和抗干扰的鲁棒性.文献[33]提出了一种基于三维建筑信息辅助的GPS 直接位置估计技术，然后分别在只有LoS 信号、LoS 信号和NLoS 信号混合、只有NLoS 信号三种场景下进行实验，结果表明在DPE中使用信号可见性和镜面反射预测可以改善定位，均方根位置误差从大约30 m 减少到10 m.

除了在处理NLoS 信号方面的应用，DPE 还有三个扩展应用：

1)联合GNSS+视觉DPE.Ng 等[34]提出通过联合GPS 和视觉直接定位(GPS+VDP)来实现GPS 和视觉位置传感的深度耦合，并且分别在开阔的天空和城市场景下进行了实验，通过分析GPSDP、Vision DP和GPS+VDP 结果，证明了GPS+VDP 的有效性.

2)多接收机DPE.Chu 等[35-36]针对多径和信号掩蔽这种非理想环境，在DPE 的基础上提出了一种多接收机直接位置估计(MR-DPE)，并利用飞机在山谷飞行的实测数据进行实验，结果表明标量跟踪接收机已经失锁，而DPE 可以保持稳定的跟踪.文中指出MR-DPE 的鲁棒性来源于多接收机框架带来的测量冗余和几何冗余，以及从DPE 继承的固有鲁棒性.此外，文中还提出了基于最大似然的姿态估计算法和在测量融合期间基于信噪比的加权，并在软件上实现，最后通过一系列飞行测试验证了该算法的有效性.

3)DTE.当用户位置固定或者用户不关心位置坐标时，DPE 的待估计参数就只剩下接收机的钟差以及钟漂，此时DPE 便退化为DTE.文献[37-38]将多接收机和DTE 结合，提出了一种基于多接收机DTE的GPS 欺骗源定位算法，不但能在欺骗信号条件下保持正确的定位和授时，还能利用粒子滤波器来定位欺骗器.此外，文献[38]做了相应的扩展，比如在干扰攻击和欺骗攻击的条件下，分别与传统标量跟踪和矢量跟踪的性能作比较，证明了MR-DTE 算法的抗攻击能力.

除此之外，还有学者借鉴DPE 的思想原理做了一些研究.文献[39]基于DPE 的联合处理的思想，设计了基于线性模型的导航域联合矢量跟踪环路架构.该环路能够减轻卫星信号受到的干扰，并解决远近效应，提高跟踪灵敏度和精度，但是由于联合矢量鉴别器的计算量大，导致该联合矢量跟踪环路不能实时实现.文献[40]推导了多卫星信号的时延和多普勒误差引起的检测损耗，比较了联合捕获与传统捕获在时延和多普勒误差下的检测损耗，并通过仿真证明了联合捕获的检测损耗总体上小于传统捕获的检测损耗.文献[41]借鉴DPE 思想，提出了一种从多卫星信号中提取导航状态误差的迭代最大似然估计方法(IMLE)，并通过蒙特卡罗模拟验证了IMLE 的有效性.

总结DPE 的三个扩展应用以及其主要原理和优势，如表3 所示.

表3 DPE 扩展应用研究状况

基于导航域通过一步估计得到导航解的特点使得DPE 相对于传统两步法更容易集成其他先验信息，因此才有了联合GNSS+视觉DPE 这一扩展应用.但是视觉信息仅仅只是其中之一，后续可以考虑将惯性导航融合进来.除此之外，也可以考虑将深度学习等智能化方法应用到DPE 上，以解决计算量庞大的问题.

2 DPE 实现面临的问题

目前DPE 主要还处于理论研究阶段，到实现应用仍存在较长的距离，但是关于DPE 实现所面临的问题，目前也做了一些分析研究.文献[30]中总结了DPE 实现需要考虑的几个实际问题，为以后的研究指明了方向.除此之外，文献[29]对DPE 实现的问题也有一些研究.本章主要对DPE 实现所面临的问题进行总结分析.

2.1 计算量庞大

DPE 通过联合所有可见卫星信号直接在导航域进行信号能量积累，并利用联合积累输出通过一步估计得到导航解.虽然基于导航域的DPE 可以实现导航参数的最优估计，但是代价却是庞大的计算量.由1.1 的原理推导可知，DPE 待估计的导航域参数是一个八维的矢量，包括接收机的三维位置坐标、钟差、三维速度以及钟漂.这意味着DPE 对PVT 的解涉及到多维非凸函数的优化问题，这个过程通常非常繁琐.

以基于网格的方法为例，DPE 的计算量主要体现在两个方面：

1)对于每一个网格点，都需要生成所有可见卫星的本地信号，并与接收信号做相关运算.在传统的M通道的标量接收机之中，一个通道跟踪一颗卫星，因此最多只需生成M颗卫星的本地信号与接收信号做相关.当可见卫星数小于M时，DPE 一个网格点的运算量就相当于标量接收机一次跟踪的运算量；当可见卫星数大于M时，DPE 一个网格点的运算量大于标量接收机一次跟踪的运算量.再考虑到网格点的数量，那么DPE 的计算量将会远高于标量接收机.因此，在如此庞大的计算量面前，DPE 很难做到实时定位解算，使用算力高的设备进行解算是最为直接的方法，但不适合于广泛应用，因此还需要在算法层面进行改进.

2)网格密度.第一点主要是分析一个网格点的计算量，这是由于DPE 自身的结构所决定的，无法改变，但是网格密度却是可以人为控制的.网格密度增大，相邻网格之间的间距减小，定位精度提高.但是相应的网格数量也会增大，计算量提高.网格密度虽然可以影响定位精度，但这种影响并非是简单的线性关系，当网格密度较大时，继续增大网格密度对定位精度的提升几乎没有影响.因此，在实际实现中，同时考虑计算量和定位精度的情况下，需要取一个合适的网格密度.值得注意的是，不同的网格模型也会对定位精度造成影响.

2.2 需要初始化

DPE 能在弱信号、多径干扰等具有挑战性的环境下保持稳定的性能，但是DPE 需要传统标量跟踪来初始化才能开始运行.而在这种复杂环境下，传统标量跟踪已无法成功定位，因此不能获得接收机的初始状态和卫星星历等先验信息，DPE 无法进行.针对这种无法初始化的情况，需要给接收机提供一些外部辅助，这个外部辅助在复杂环境下仍能提供DPE 所需要的先验信息，例如接收机位置、周内时(TOW)、星历表、多普勒频移、卫星时钟校正等.

此外，对于可以利用标量跟踪初始化的情况，也需要分析初始化的准确性对DPE 性能的影响.DPE的成本函数如图5 所示，如果DPE 初始值能落在成本函数的主瓣中，那么对于公式(7)的优化基本就能确定可以达到全局最优解；如果初始值位于主瓣之外，那么很可能会得到一个局部最优解.对于图5 而言，初始值的误差要小于±300 m，这个初始值误差的门限取决于成本函数的主瓣宽度.而根据公式(7)，主瓣宽度取决于信号自相关函数的宽度，具体来说取决于伪码速率，伪码速率越高，主瓣宽度越窄.±300 m是一个比较宽松的范围，而对于实际信号而言，初始值的误差门限可能需要小到几十米.

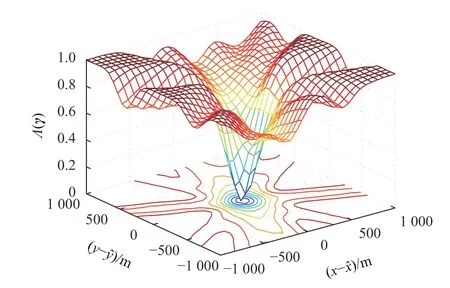
图5 DPE 成本函数[30]

2.3 其他问题

上述提到的两个问题是DPE 走向实现和应用需要迫切解决的主要问题，除此之外，考虑到接收机的适用性、完好性等因素，DPE 实现还存在一些其他问题.

1)多星座、多频点接收的问题，即接收来自不同导航系统的信号或接收同一导航系统内不同频点信号的能力，多星座、多频点接收有助于提高导航接收机在恶劣环境下的可用性.但是这需要额外考虑如何估计和获取不同星座之间的时钟偏差，增加了复杂度和计算负担.

2)多传感器信息融合问题.DPE 利用接收机状态来参数化信号模型，而不是依靠同步参数，这种特性不仅带来了性能上的提升，而且让接收机更容易利用一些先验信息.比如考虑一个简单的应用场景，DPE 可结合地图匹配技术，排除掉一些接收机不可能到达的地点，从而减少DPE 的计算量.

3)接收机自主完好性监控(RAIM)问题，即根据接收机的冗余观测值监测定位结果的完好性，其目的是在导航过程中检测出发生故障的卫星，并保障导航定位精度，这对接收机安全尤为重要.目前主要分为两条路径，一个是将原有的针对传统接收机的RAIM算法应用于DPE 上[42]，但是可能存在适配性的问题.由于DPE 对位置的鲁棒性这一特点，在位置误差较小时使得故障卫星很难被检测出来.另一个方法是提出新的适用于DPE 的RAIM 算法[43-44]，这种针对DPE 的特殊框架开发的RAIM 算法通常能获得更高的适用性.

3 复杂环境下的DPE 接收机设计

DPE 旨在克服传统接收机在弱信号和干扰等复杂环境下无法正常工作的缺点，但是在这种复杂的环境下，DPE 的性能或多或少也会存在一定程度的下降，因此需要评估接收信号的可用性和可靠性，以保证DPE 输出的定位结果是正确的.

3.1 弱信号场景

对弱信号的鲁棒性是DPE 最为显著的优点，这个优点源自于DPE 本身的结构，无需人为地增加相应算法或外部辅助等额外代价，因此DPE 方法尤其适用于弱信号环境.目前的研究已经证明了相较于传统两步法，DPE 在弱信号下仍然保持较好的定位性能.但是信号强度的衰减，必然会导致信号相关幅值减小，相关峰的尖锐程度降低，而由于峰值点周围的网格能量近似，再加上噪声的影响，正确位置的估计可能会落在邻近栅格，最终导致位置估计精度降低.信号强度越低，DPE 的误差也会越大，因此在给定一个误差容忍范围的前提下，探究DPE 接收信号强度的下限也是一件很有意义的工作，对于DPE 在弱信号环境下的性能也可以给出一个定性的结果.反之，也可以将信号强度作为评估DPE 定位结果可靠性的一个重要依据，当信号强度低于阈值时，可以认为此时的定位结果不可靠.

3.2 干扰场景

干扰主要分为压制式干扰和欺骗式干扰[45].所谓压制式干扰，就是用干扰机发射干扰信号，以某种方式遮蔽GNSS 信号频谱，使敌方GNSS 接收机降低或完全失去正常工作能力[46].在传统方法中，一般需要对针对不同干扰的特征来设计不同的抗干扰算法，以达到对干扰的有效抑制[47-48].但是对于DPE 而言，压制式干扰类似于弱信号场景，即信号解扩后依然淹没在噪声之中，由于DPE 是对信号的联合积累，在这种情况下依然能保持很好的定位性能.因此，理论上DPE 对于压制式干扰也会有鲁棒性，但是依然面临着和弱信号场景同样的问题，即随着压制干扰功率的不断增大，DPE 的误差也会相应增大，在给定一个误差范围的前提下，DPE 能容忍的压制式干扰的功率也存在一个上限.

欺骗式干扰是指发射与GNSS 信号具有相同参数的虚假信号，使GNSS 接收机在不知不觉中输出虚假的定位授时信息.欺骗干扰攻击比压制式干扰更具危害性，因为欺骗攻击甚至不会使接收机产生任何告警信息，这可能会给用户造成严重危害[49-50]，因此对于欺骗信号的检测是可信导航的一个关键点.以基于网格的DPE 为例，当欺骗信号作用于DPE 接收机时，会在欺骗位置对应的网格点处有较大的幅值，幅值的大小取决于欺骗信号的数量和强度，网格相关值如图6 所示.此时，DPE 的相关结果会从单峰变成双峰甚至多峰，因此直接把相关结果作为DPE 的欺骗检测量是比较直观且简易的欺骗检测方法，但是这种检测方法对欺骗位置和真实位置的间距有要求.如果欺骗位置和真实位置相隔太近，那么相关结果也会呈现单峰状态，根据上述方法则会造成漏检.后续研究可以考虑将原有的针对传统两步法的欺骗检测方法应用到DPE 上，或者针对DPE 的结构提出新的欺骗检测方法.

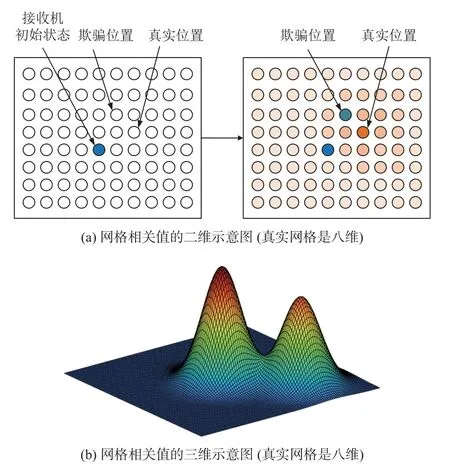
图6 DPE 接收机接收欺骗信号的示意图

3.3 接收机结构

传统标量跟踪结构简单、实现成本低，但是在复杂环境下定位性能会下降甚至无法定位.而DPE 能够克服传统标量跟踪这一缺点，但是计算量太大，需要耗费更多的算力资源，实现成本较高.因此，综合传统标量跟踪和DPE 的特点，本文提出了一种适用于复杂环境的接收机设计框架，如图7 所示.该接收机架构包括了传统标量跟踪和DPE，正常情况下，接收机会一直进行标量跟踪来获得定位授时结果.当信号可用性降低、标量跟踪定位性能下降或者无法定位时，接收机则启用DPE.下面对上述复杂环境DPE 接收机结构的主要部分进行介绍.

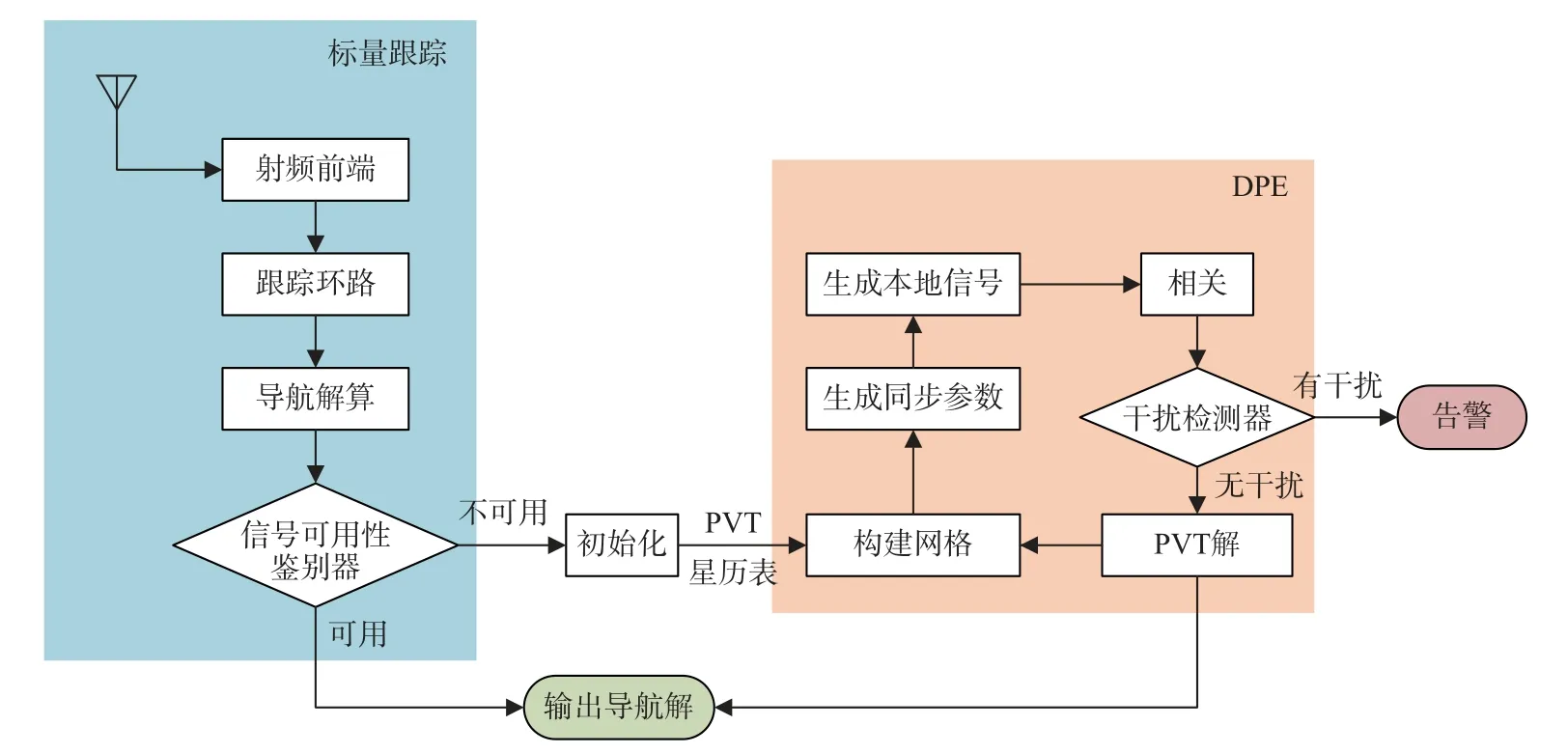
图7 复杂环境 DPE 接收机结构

初始化：DPE 需要初始化，初始化信息可以由传统的标量跟踪或其他传感器提供.

信号可用性鉴别器：信号可用性体现在多个方面，例如信号强度的高低、噪声功率的大小以及多径干扰的严重程度，因此对于应用在不同场景的接收机可以设置不同鉴别标准的信号可用性鉴别器.以弱信号环境为例，鉴别器可以根据接收信号计算出载噪比，如果载噪比低于一定门限，那么就认为信号不再可用，此时即可启用DPE 继续进行导航定位.

干扰检测器：考虑到DPE 主要应用在传统接收机无法正常工作的复杂环境之下，因此有必要在DPE 中加上一个干扰检测器，当检测器检测到干扰信号的存在时，就向用户发出警告，以便用户采取进一步的应对措施，如果没有检测到干扰则继续DPE 的进程.该检测器主要针对多径干扰和压制干扰，在特定场景下，也可以考虑欺骗干扰的影响.

4 结束语

DPE 作为导航领域的一个新兴技术，能够克服传统方法在高楼矗立的城市、室内等复杂环境下无法正常工作的缺点，但是目前关于DPE 的研究还比较少，主要偏向于理论性能方面，距离实现应用仍有不少距离.本文主要对DPE 的研究现状以及DPE实现所面临的几个问题进行了总结归纳.DPE 具有高灵敏度、抗多径干扰等出色性能，并且在高动态、欺骗干扰场景的表现也很好，适用于复杂环境.但是DPE 实现还需克服计算量庞大、定位精度较低、需要初始化等问题.最后本文综合传统标量跟踪和DPE的优缺点，将DPE 作为一种非常规的导航定位方法，提出了一种适用于复杂环境的接收机设计框架.该接收机可以实现对信号可用性以及可靠性的评估，根据评估结果来决定是否由标量跟踪切换到DPE，在消耗尽量少的算力资源下提高接收机在复杂环境下的定位性能.上述研究成果可为后续研究DPE 的性能、实现以及提升复杂环境下GNSS 导航定位的可靠性提供有力支持.