结合CNN-BiLSTM-SA 运动模式识别的自适应步频检测方法

杨运成，吴飞，朱海，朱润哲，杨明泽

(上海工程技术大学 电气电子工程学院,上海 201620)

0 引言

近年来，随着信息技术的飞速发展，位置服务(LBS)已经成为人们日常生活和工作中不可缺少的一环[1].在室外情况下，全球卫星导航系统(GNSS)已经满足人们的需要，但是由于建筑物信号遮挡和多径效应等问题，导致GNSS 在室内无法得到有效定位.目前，有许多室内定位方法如Wi-Fi[2-3]、蓝牙[4]、超宽带(UWB)[5-6]都是基于无线电信号获取位置，然而这些技术需要部署特定的基础设备，并且成本与所需定位面积成正比，这些室内定位技术在广泛普及应用中有一定局限性[7].因此，不依赖提前部署定位设备的基于智能手机的行人航迹推算(PDR)室内定位方法得到广泛关注和研究，它独立性强且适用于未知环境.

如何实现具有鲁棒性和高精度的步频检测是PDR 定位技术的重要一环.通常，行人在行走时携带手机的位置不是单一固定的，常见携带位置包括手持胸前、手臂摆动、打电话和放入口袋.同时，行人在非行走状态下操作同样产生假步行状态导致计数过多问题，因此，对识别出行人运动模式且针对不同模式自适应阈值的步频检测的研究具有重要意义.在运动模式识别相关研究中，文献[8]利用加速度数据的斜率区分跑步和行走模式，然后选择适合的模型参数.文献[9]使用有限状态机对手机姿势分为摇摆、手持和口袋三类，准确率为89%.文献[10]设计一个随机森林分类摆臂、包内和上下衣口袋四种模式，准确率为93.7%.然而上述方法都需要人为从原数据中提取特征，需要运动模式与特征之间的先验知识.近年来随着深度学习的发展，深度学习网络逐渐运用到人类的活动识别中，文献[11]提出一种基于循环卷积注意力网络框架，有效识别人类多种日常活动，然而该方法需要在人体多个部位绑定传感器装置.文献[12]采用多头卷积神经网络(CNN)进行运动模式识别，利用多头注意力机制学习卷积网络的时间序列间的相关性，但是文中只用来识别五种基本步行模式.在步频检测相关研究文献中，峰值检测[13-14]、阈值检测[15-16]和自相关法[17]是常用的计步方法.文献[18]通过低通滤波和平滑滤波减少行人相对抖动的影响.文献[19]通过设置振幅阈值和时间间隔阈值解决计数过多问题，但提前设置固定阈值很难适用于不同的运动模式.文献[20]利用支持向量机(SVM)分类运动模式动态调整算法的参数，虽然正确识别下的计步算法准确率达到98%，但是SVM分类器准确率只有85%.

基于上述问题，本文综合CNN 和自注意力(SA)机制在行人运动信息提取和选择的高效特点[21]，以及双向长短期记忆网络(BiLSTM)在具有时间序列数据上的优异表现[22]，提出一种结合CNN-BiLSTM-SA 运动模式识别的自适应步频检测方法：首先，运动模式划分为正常行走和快走两种运动状态以及手持、通话、摆臂和口袋4 种手机姿势，通过手机内置加速度计和陀螺仪获取行人当前运动下的三轴加速度和三轴角速度数据.使用CNN 自动提取原数据特征信息，利用SA 机制对提取的特征进行权重分配，再结合BiLSTM在前后时序中对潜在特征信息的挖掘，可以更好地对行人不同运动模式进行识别.其次，针对手机内置低精度传感器和行人身体相对抖动产生的伪波峰噪声，提出一种二重加速度滤波器的预处理方法，先利用截止频率为3 Hz 的低通滤波器过滤大量伪波峰，再使用卷积平滑滤波器二次平滑数据，得到更利于步频检测的运动模型.最后，通过实验识别行人的不同运动模式类型，结果表明：本文提出方法能有效识别运动模式和在不同模式下均有较高的步频检测精度.

1 运动模式识别

一般来说在行走过程中，行人不同的运动状态和手机的持有方式会产生不同的波动特性，单一的步频算法难以适用于不同运动模式.因此，为了通过识别出行人不同的运动模式来优化步频算法，提高步频检测的准确性和鲁棒性，本章节提出一种基于深度学习的分类算法，对行人运动中的加速度和角速度信息进行模式识别.流程共分为两个步骤：第一步，对运动状态和手机姿势的定义分类；第二步，利用采集的传感器数据训练分类器模型，并使用模型进行分类识别.

1.1 运动状态和手机姿势划分

由于传统单一模式下的步频检测算法并不适用于多种运动模式，因此本文根据行人日常运动和使用手机的习惯将运动模式分为两类：运动姿态和手机姿态.运动状态代表行人在行走中的速度习惯，分为正常行走和快走.手机姿态代表行人使用手机的姿势，包括手持、通话、摆臂和口袋四种，如图1 所示.

(a)手持：行人走路时将手机在胸前自然持有；

(b)通话：行人在走路时接保持通话状态；

(c)摆臂：行人在走路时手握手机自然摆动，根据手机使用习惯，假设手机屏幕指向身体一侧；

(d)口袋：行人走路时，手机被放置裤子口袋里.

其中运动状态和手机姿势相互独立，可以产生八种组合模式.分别为手持正常行走、手持快走、通话正常行走、通话快走、摆臂正常行走、摆臂快走、口袋中正常行走、口袋中快走.

图2 显示了正常行走下使用四种手机姿态的惯性传感器特性.从数据中体现出行人在同一运动状态下利用不同手机姿态，其加速度和角速度传感器不同的数值和波动变化.因此，可以充分利用这种差异性来识别不同的手机姿势.

图2 不同运动姿态下惯性传感器特性

1.2 CNN-BiLSTM-SA 模型

通常行人运动产生的数据复杂多样，需要利用合适的分类器来识别不同运动模式.在常见方法中，通常使用如决策树、随机森林、SVM 和人工神经网络等机器学习方法[23].虽然这些传统的分类器可以识别不同运动活动，但识别准确率主要依赖从源数据中人工提取的不同类型特征，如统计特征(例如均值、方差、能量)、时域特征(例如过零比)、频域特征(例如快速傅里叶变换(FFT))[24].并且不同类型特征对不同运动模式的敏感度不同，若选取合适特征则需要大量经验积累，很难推广到其他模型.

因此，为了提高运动识别准确率、增强识别鲁棒性、减少人为提取特征的影响，本文提出一种无需从源数据二次提取特征的CNN-BiLSTM-SA 深度网络框架模型，结构模型如图3 所示.

1.2.1 CNN 层

为了从行人运动产生的加速度、角速度数据中自动提取局部关键特征，首先使用具有高效网格数据分析能力的CNN 进行处理.CNN 的核心为卷积层和池化层，首先通过卷积层中的卷积核对加速度和角速度数据进行卷积操作，提取出与之对应的运动特征信息.由于真实环境下运动状态是非线性的，因此，引入ReLU 激活函数带来非线性能力.最后在池化层中选用最大池化层，进一步压缩和聚合从卷积层提取的特征，降低特征维度的同时也能保留关键特征信息.

1.2.2 BiLSTM 层

BiLSTM 是基于长短期记忆网络(LSTM)的一种扩展模型[25]，由于LSTM 为单向传输，在时序上只能完成从过去时刻到未来时刻的分析.然而当行人行走时，每一步动作姿态内有较强前后关系，尤其行人在运动模式切换过程中，前后会产生较大数据突变，因此，采用由正向LSTM 和反向LSTM 结合的BiLSTM 网络.相对单向LSTM，BiLSTM 具有丰富时序分析能力，能更充分地分析行人运动姿态前后之间的关联性.

单层BiLSTM 如图4 所示，正向LSTM 保留行人过去到未来时刻的重要信息，反向LSTM 保留行人从未来到过去时刻的重要信息，且传输公式为：

图4 单层BiLSTM 模型结构

1.2.3 SA 层

SA 本质是从大量信息中提高关键特征信息的权重，减少不重要或不相关信息.由于运动中采样的三轴加速度和角速度信息在不同运动模式中对应不同轴数据的敏感程度也不同，因此，如图5 所示引入SA 层，输入的特征分配不同权重.

图5 SA 模型结构

本文在CNN 层后加入SA，首先对CNN 输出的特征矩阵进行空间映射，然后通过相似度计算得出SA 分数，再使用SoftMax 将分数归一化处理，最后将得到的结果进行加权求和得到全局的特征信息.其计算过程如下.

1)对每个输入X=[x1,···,xN]∈RDx×N映射到三个不同空间分别得到查询向量、键向量和值向量矩阵Q、K和V，计算公式为：

式中，Wq、Wk和Wv分别为线性映射的参数矩阵.

2)利用得到的Q和K的转置点积计算输入特征间的相关性分数S，并引入K的维度Dk使得点积计算结果平滑，从而在训练中保持梯度稳定.其中分数S计算公式为

3)使用SoftMax 归一化处理为概率分布矩阵，再点积V得到输出特征矩阵H：

2 步频算法

2.1 数据预处理

由于手机内部使用的廉价惯性传感器测量精度较低，且传感器在数据采集中又受行人相对运动过程中身体抖动的影响，使得采集的原始数据中存在大量噪声，同时会造成伪波峰影响步频检测的计步精度.因此，在进行步频检测前，需对原始数据进行预处理，减少部分伪波峰.本文设计一组两种滤波的组合：低通滤波和卷积平滑滤波.先利用低通滤波减少原始数据中的噪声，消除明显伪波峰；再使用卷积平滑滤波二次平滑数据，得到更利于步频检测的运动规律.

由于单轴加速度易受手机方向影响，因此使用三轴的合加速度，即

式中，ax、ay和az分别是x轴、y轴和z轴的加速度大小.

为了消除噪声影响，先利用过滤噪声消除大量伪波峰.然后利用卷积平滑滤波，即通过线性最小二乘法将相邻数据点的连续子集与一个低次多项式拟合，在不改变信号趋势下提高数据精度，平滑数据得到更利于步频检测的运动规律.其公式为

式中：Yj为过滤后值；Ci为卷积系数；m为多项式拟合阶数.

如图6 所示，图6(a)中初始加速度信号中存在多个伪波峰，这些伪波峰是造成计步较多的重要原因之一.与原始数据相比，图6(b)中第一阶段在通过低通滤波后，可以过滤干扰噪声消除大量伪波峰；图6(c)中第二阶段为再次使用卷积平滑滤波器二次滤波，伪波峰数量减少同时波形显得愈加平滑，更加清晰地反映出行人运动的规律和特征.

图6 加速度数据预处理

2.2 峰值检测

由于行人在行走时身体重心在垂直方向上下波动，因此合加速度数据呈现具有波峰波谷的周期性振荡特性，传统的峰值检测是根据加速度数据的波峰个数来确定行走步数.尽管通过滤波能消除大部分由于运动方式和身体抖动等因素产生的大部分伪波峰.但是依旧存在部分伪波峰会导致计步过多问题.因此，本文利用两种约束条件：最小峰距和自适应阈值对传统的峰值检测进行约束，通过分类器识别出不同运动模式，根据不同运动模式对最小峰距和自适应的阈值进行相应调整，进一步提高峰值检测算法的鲁棒性.

2.2.1 最小峰距

即使数据预处理后能过滤大量噪声，但在两峰值之间依旧存在部分未被过滤的伪波峰.基于传统峰值检测的方法会将这些伪波峰纳入正常计步而增加误差,因此根据相同运动模式下运动周期一致且峰值是当前步骤下的局部最大值，使用最小峰距去除相邻峰内的其他波峰数，计算过滤后峰值Pt为

式中：at为在t点样本下合加速度值；k为t点左右两侧的样本数量阈值，k值应小于两个真实波峰之间的样本数.由于正常行走和快走时运动周期频率不同[26]，因此行人在两种运动状态下产生的真实波峰间样本数也不同，使用固定阈值k限制最小峰距会造成计数误差问题.

根据实验数据分析，如图7(a)所示，当设置阈值k=10 时，行人在快走中步频算法的峰值等于真实步数，但切换到正常行走中由于阈值设置过小会引入未被过滤的伪波峰(绿色圈)，增加伪步数统计；图7(b)显示了当设置阈值k=20 时，行人在正常行走下能过滤伪波峰精确计步，但切换到快走中由于阈值设置过大而忽略其中的真峰值(绿色圈)，从而减少真实步数统计.

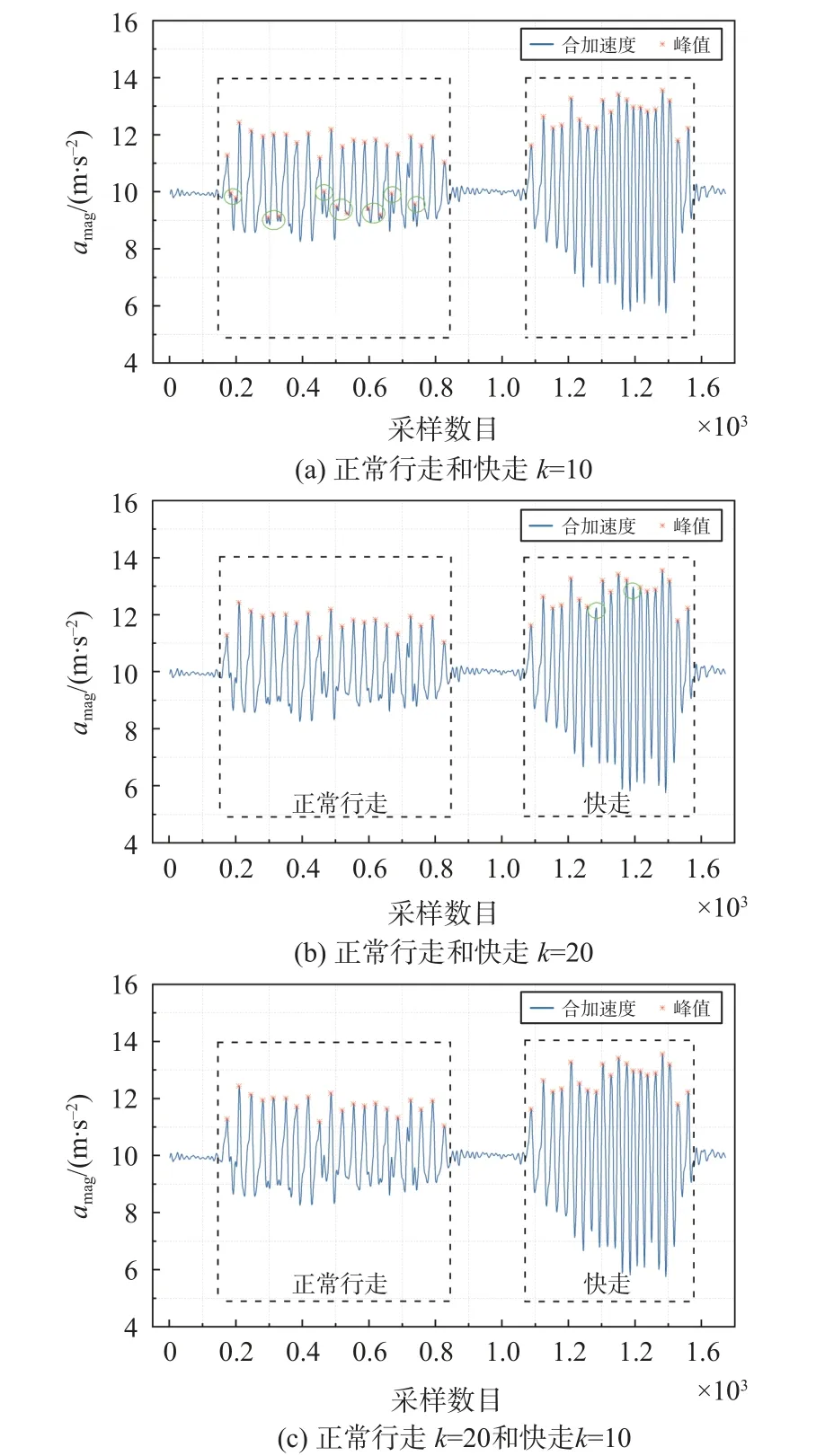
图7 不同k 值下峰值

因此，本文在最小峰距算法中提出自适应阈值，先根据运动模型检测出当前运动状态属于正常行走还是快走，并自适应调整最小峰距k值.根据实验结果，本文设置正常行走模式下k=20，快走模式下k=10，如图7(c)所示，在不同运动模式下有效利用不同阈值可获得更高精度检测.

2.2.2 自适应动态阈值

行人在行走过程中使用不同手机姿态传感器数据会产生不同周期性特征.手持模式下，实际的每一步过程中先出现一些小波峰，再出现一个较大波峰.这些大波峰对应真实的一步，影响计步的小波峰需要作为伪波峰消除.而在口袋模式下实际的每一步中，会先出现一个大波峰，再出现一些小波峰，接着出现一个中波峰，作为需要真实计步的波峰呈一大一中规律.在传统固定阈值设置方法中，设置较小固定阈值会引入伪波峰加入计步，设置较大固定阈值会将把口袋模式下的中峰作为伪波峰排除计步.因此，本文提出一种自适应的动态阈值法，能有效提高不同运动模式下计步精度.

动态阈值法基于在一个窗口内的加速度最大值和最小值构建动态阈值，其中窗口尺寸大小取决于行人的运动状态和采集频率，不同的窗口大小同样影响阈值精度.在一般情况下，正常走与快走的每步平均时间[26]如表1 所示.

表1 每步平均时间

根据不同运动状态下的每步时间Ts和当前手机采样频率Fs设置窗口尺寸公式如下：

式中：TH为当前窗口下计算的动态阈值；Wmax为当前窗口的最大值；Wmin为前窗口最小值；d为趋近峰值程度，由于手持和电话姿势每一步波峰振幅大致相同，而口袋和摆臂姿势每步波峰呈大小峰形式，因此根据实验结果设置手持和电话姿势下d=1.05，口袋和摆臂姿势下d=0.9.再将经过最小峰距过滤后的峰值与窗口内的动态阈值作比较，若当前峰值大于等于在此窗口内的动态阈值TH，则计为真实一步.

如图8 所示，行人在正常行走下加速度值普遍小于快走模式，且使用摆臂姿势下波峰呈现一大一小状态.因此使用固定阈值会忽略真实波峰或引入伪波峰，难以适应不同运动模式下需求，而通过本文设计的自适应阈值法，根据分类器检测的不同运动模式计算当前窗口下的自适应动态阈值，具有更精确的步频检测精度和更健壮的鲁棒性.

图8 摆臂姿势下峰值

3 实验与分析

为了验证本文提出的运动模式识别模型和步频检测算法的有效性，实验采用设备是基于安卓12 系统的OPPO Reno6pro 智能手机，手机内置三轴加速度计和三轴陀螺仪，传感器输出频率Fs设置为50 Hz.

实验选择5 名行人，身高为1.65～185 m.根据第2 节划分行人日常习惯，分别为正常行走和快走运动状态，手持、通话、摆臂和口袋四种手机姿态共八种组合运动模式，5 位行人分别以每个运动模式按直线走60 步，则每位行人实际行走步数为480 步.

为了验证模型识别效果，本文测试5 名行人共采集到69 878 条实验样本数据，每条信息包含三轴加速度(ax、ay、az)和三轴角速度(θx、θy、θz)共6 种特征数据值.依次将每30 条(约2～3 步)制作成尺寸30×6 的二维切片数据，并按八种运动模式标签分类.其中选择70%条切片样本为训练集，选择30%条切片样本为测试集测验模型分类结果.

3.1 不同卷积层的识别精度对比

为了分析CNN-BiLSTM-SA 模型中不同卷积层数对模型识别的影响，本文设计不同层数进行对比实验，分别用分类交叉熵损失函数和准确率作为评价标准，交叉熵是用来评估当前训练得到的概率分布于真实分布之间的差异情况，其值越小代表两个概率分布越接近[27].

实验中使用1～4 层CNN 卷积层的模型识别交叉熵损失值和准确率，分析不同层数对识别精度的影响，实验结果如表2 所示.实验结果表明，使用不同深度的CNN 卷积层对于模型识别精度具有不同的影响.根据交叉熵损失值的结果，相较于使用1 层、3 层和4 层CNN 卷积层，使用2 层CNN 卷积层的交叉熵损失值最低为0.088 1.同时，根据准确率结果，使用2 层卷积层模型的准确率为98.52%，分别比使用1 层、3 层和4 层卷积层模型的准确率高0.67%、0.48%和1.35%.实验证明了2 层卷积层识别精度均高于其他网络层数，并且增加层数并没有使识别精度提高，反而会增加模型复杂度和过拟合，从而降低识别效果.

表2 不同CNN 层数的识别精度对比

3.2 运动模式识别实验

为了进一步验证模型有效性，本文分别采用决策树、随机森林、CNN、CNN-LSTM 和本文CNNBiLSTM-SA 共五种模型进行对比实验，选择识别准确率作为评价标准，结果如图9 所示.可以看出相对传统决策树、随机森林方法，在仅输入原始加速度、角速度数据而未使用人工二次提取特征情况下，识别准确率明显低于深度学习模型，而对比同类深度学习模型CNN 和CNN-LSTM，本文方法准确率分别提高了3.04%和2.21%.

图9 五种分类模型准确率结果

为了进一步验证CNN-BiLSTM-SA 模型的分类效果，将三种深度学习网络模型进行定量分析.在相同实验环境下，设置初始学习率均为0.005，批尺寸batch-size 为64，迭代轮次epoch 为200，使用he_uniform 方法初始化每层网络权重和偏置.训练过程如图10 所示，实验结果表明，本文CNN-BiLSTMSA 模型准确率明显优于CNN 和CNN-LSTM 模型，在识别行人运动模式上有更好的表现.

图10 三种深度学习模型训练过程对比

3.3 步频实验

为了探究本文滤波组合对数据噪声引起伪波峰的过滤有效性，实验分别对无滤波、低通滤波、卷积平滑滤波和低通卷积平滑组合滤波对噪声引起伪波峰的优化情况进行对比.由于噪声存在与行人间的差异无关，实验随机选取1 名行人正常行走下的四种运动模式，每种模式直线走60 步，即真实波峰值为60.实验结果如图11 所示，当未使用滤波对原采集数据预处理时，会产生大量伪波峰，导致总波峰数严重失真偏离真实；当单独使用低通滤波和卷积平滑滤波时，过滤效果明显降低，在口袋模式下低通滤波明显优于卷积平滑滤波，而在摆臂模式下卷积平滑滤波略优于低通滤波；当使用低通-卷积平滑组合滤波时，滤波效果明显优于使用单一滤波器，四种运动模式下相对低通滤波平均提升10.25%.

图11 不同滤波下波峰数量对比

在步频检测实验中，考虑到不仅由于伪波峰引入伪真值，同时会由于不同阈值设置而忽略部分真值，因此引入正误差数Splus表示算法检测中过多伪真值个数，负误差数Sminus表示被忽略的真值个数，实验中步行估计误差计算为

式中，Strue为行人实际行走步数.

表3 通过实验对比了传统峰值检测法、固定阈值法和本文提出方法的误差.实验结果表明，传统峰值检测法平均误差率为7.28%，是四种方法中误差最大的.基于固定阈值法误差率受事先选定阈值影响，当TH=10 时，选择的固定阈值偏小使得检测的正误差数过多，平均误差率为4.38%；TH=11 时，平均误差率为2.21%，但选择的固定阈值偏大使得漏检的总负误差数高达14 次，综合说明事先固定阈值难以适应不同行人和不同运动模式.本文方法在八种组合运动模式下平均误差率为1.31%，且平均每位行人仅出现一次负误差数统计，实现不受运动模式变化影响的精确步频检测.

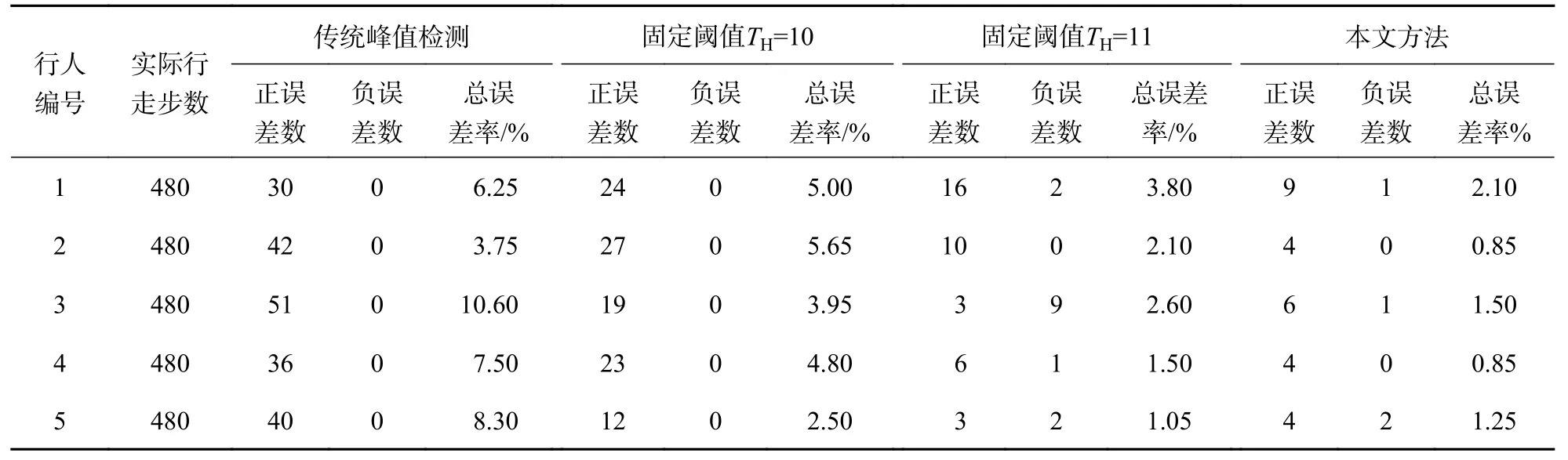
表3 5 名行人步频检测结果

图12 统计了5 名行人在四种手机姿势模式下的四种方法误差率，结果表明在电话和手持模式下，四种方法误差率相对较低，而口袋和摆臂模式下由于加速度轨迹呈现一大一小运动规律，传统波峰检测法和固定阈值法在这种复杂规律下误差率上升，而本文方法由于阈值的自适应调整在不同模式下均有最好步频检测性能表现.

图12 5 名行人不同模式误差率

4 结束语

本文提出一种结合CNN-BiLSTM-SA 运动模式识别的自适应步频检测方法.该方法使用CNN 自动提取行人运动的局部特征信息，利用SA 对提取的特征进行权重分配，再结合BiLSTM 对特征前后时序学习的特点来识别行人不同运动模式类型.然后根据识别结果，引入基于最小峰距和自适应动态阈值的步频检测算法，对不同分类结果初始化算法参数，显著提升步频检测算法的准确性和鲁棒性.实验结果表明，本文提出方法在八种组合运动模式下平均误差率为1.31%，优于传统峰值检测和固定阈值法.但本文方法是基于行人在平坦地面上的常见八种运动状态模式，未来工作可研究行人在复杂环境、复杂运动下如上下楼梯或跑步跳跃等情况.