BDS-3 多频非差非组合精密定轨精度分析
景鑫,李建文,周舒涵,蔡巍,柯能
(1.信息工程大学地理空间信息学院,郑州 450001;2.西安测绘总站,西安 710054)
0 引言
用户进行精确导航、定位和授时(PNT)所需的精密轨道产品主要通过国际GNSS 服务(IGS)组织等获取.目前,精密轨道确定主要采用双频无电离层组合模型(IF)[1].随着全球卫星导航系统(GNSS)的不断发展,越来越多的导航系统能够提供更多频点的信号[2-3].北斗三号全球卫星导航系统(BDS-3)于2020 年7 月31 日开通服务[4],能够发射五个频点信号,分别是B1I(1561.098 MHz)、B3I(1 268.52 MHz)、B1C(1575.42MHz)、B2a(1176.45MHz)、B2b(1207.14 MHz).多频IF 组合模型存在频率组合繁杂、可扩展性差的问题,难以适应日趋丰富的多频点信号资源[1].文献[5]证明加入新的频点对定位精度有所改善,而对于定轨精度的影响,研究相对较少.
非差非组合因其能够充分利用多频点观测数据,观测模型简洁、表达形式统一、易扩展且不放大噪声等特点,成为近十年来的研究热点.文献[3]对多系统非差非组合精密单点定位(PPP)理论方法进行了系统的阐述和研究.文献[6]通过非差非组合观测模型实现了低轨卫星的精密定轨.文献[7]使用非差非组合模型对GPS、Galileo、GLONASS 三个系统进行了精密定轨处理,对电离层和模糊度处理进行了论述,通过与精密产品对比,证明其轨道产品精度与IGS各分析中心产品的精度相当.文献[8]通过使用三频信号对GPS、Galileo、北斗二号卫星导航系统(BDS-2)进行了精密定轨,分析了第三频点信号对定轨精度的影响.目前国内外对BDS-3 非差非组合精密定轨研究较少,尤其是BDS-3的多频信号对定轨精度的影响、新体制信号B1C 和B2a 的定轨精度,以及不同测站分布不同频率选择时BDS-3 定轨精度的分析和研究都相对较少.
因此,本文对非差非组合观测模型和参数估计方法进行了简要介绍,通过K 均值聚类算法(K-means)优化测站选取策略,对数据处理过程中的误差和模型进行描述,通过两种实验方案,采用五频、B1C+B2a、B1I+B3I 三种频率选择方式进行精密定轨,并对BDS-3 不同测站分布、不同频率选择的定轨精度进行了对比分析.
1 非差非组合定轨方法
1.1 观测模型
标准单系统GNSS 观测模型的伪距和载波相位观测方程可表示为:
式中:下标fre为所选频点;为站星几何距离,指卫星天线相位中心到接收机天线相位中心的几何距离,单位为m;c为真空中的光速;δtr和δts为接收机和卫星钟差;为对流层和电离层延迟;Br,fre和为接收机和卫星伪距硬件延迟;为残差;λfre为波长;br,fre和为接收机和卫星载波相位延迟;Nfre为载波相位整周模糊度.
在精密定轨数据处理中,公式(1)~(2)中的观测模型需要通过泰勒级数展开进行线性化处理,重组后的观测方程为:
1.2 参数估计方法
非差非组合方法直接利用观测方程构建方程组进行参数估计、参数估计是通过函数模型利用获取的观测值确定未知参数的过程.在GNSS 数据处理中,函数模型即为观测方程,参数估计方法一般采用最小二乘平差方法,具体过程如下.
首先,将公式(3)~(4)的函数关系简化为
式中:L为伪距和载波相位观测值;f(X)为观测量和未知参数之间的函数关系,X为未知参数;e为残差.
通过将观测方程进行线性化,将其在初始状态处进行泰勒展开,截断高阶项,可得如下简化的线性方程:
令ΔL=L-f(X0),ΔX=X-X0,则式(6)可化简为
观测值的协方差矩阵为ΣL.将矩阵求逆可得权矩阵,σ2为先验方差因子,初始值可设置为1.则加权的最小化残差平方和为
使式(8)最小化可得法方程:
在求解非线性最小二乘平差时,一般通过不断迭代提高参数估计精度,最终获得参数估计解.
2 处理策略
2.1 K-means 算法测站选取策略
将数据样本按照数据之间的内在关系划分为若干类别的算法称为聚类算法,K-means 是其中最基础的聚类算法[9],是一种将向量距离作为相似性评价指标,进行类簇划分的方法.向量距离即为每一个样本到每一个聚类中心的距离,一般采用欧式距离[10],公式如下:
式中:D(Xi,Cj)为第i个样本到第j个簇类中心的距离;xi,lon,cj,lon和xi,lat,cj,lat分别为第i个样本和第j个簇类中心的相关属性.
K 值代表其需要划分的聚类个数,means 代表取聚类中所有样本在各个属性维度的均值作为该簇的中心[10],公式如下:
式中:Cj为第j个聚类的中心;nj为第j个聚类的样本个数;Sj为第j个聚类;Xi为第j个聚类中第i个样本.
通过计算样本与簇类中心的距离,将样本划分到距离最近的簇类中,再更新簇类中心,不断迭代,最终完成分类.
具体算法流程如下:
1)从样本中随机选取K个对象作为初始簇中心;
2)计算每个样本与K个簇中心的距离;
3)根据距离结果,将所有样本分类到离它最近的簇中心;
4)对重新划分好的聚类重新计算簇中心;
5)重复2~4 步骤,直到簇中心不再发生变化.
测站分类计算中,首先获取测站数据,其中包括测站站名和经纬度信息;然后通过K-means 算法进行测站分类后,输出结果文件,其中每个簇类中的测站会按照离簇类中心距离由近及远进行排序;最后,按照需要从每个簇类中选取测站,形成测站使用列表.
图1 为当K=30,通过K-means 算法对全球支持北斗的测站(IGS 官网数据)进行簇类分类的结果.图中圆圈为测站标识,不同颜色表示为不同的簇类,K=30,即分为30 个簇类,因此图中共有30 种颜色.从图1 可以看出分类效果较好,簇类分布较为均匀.
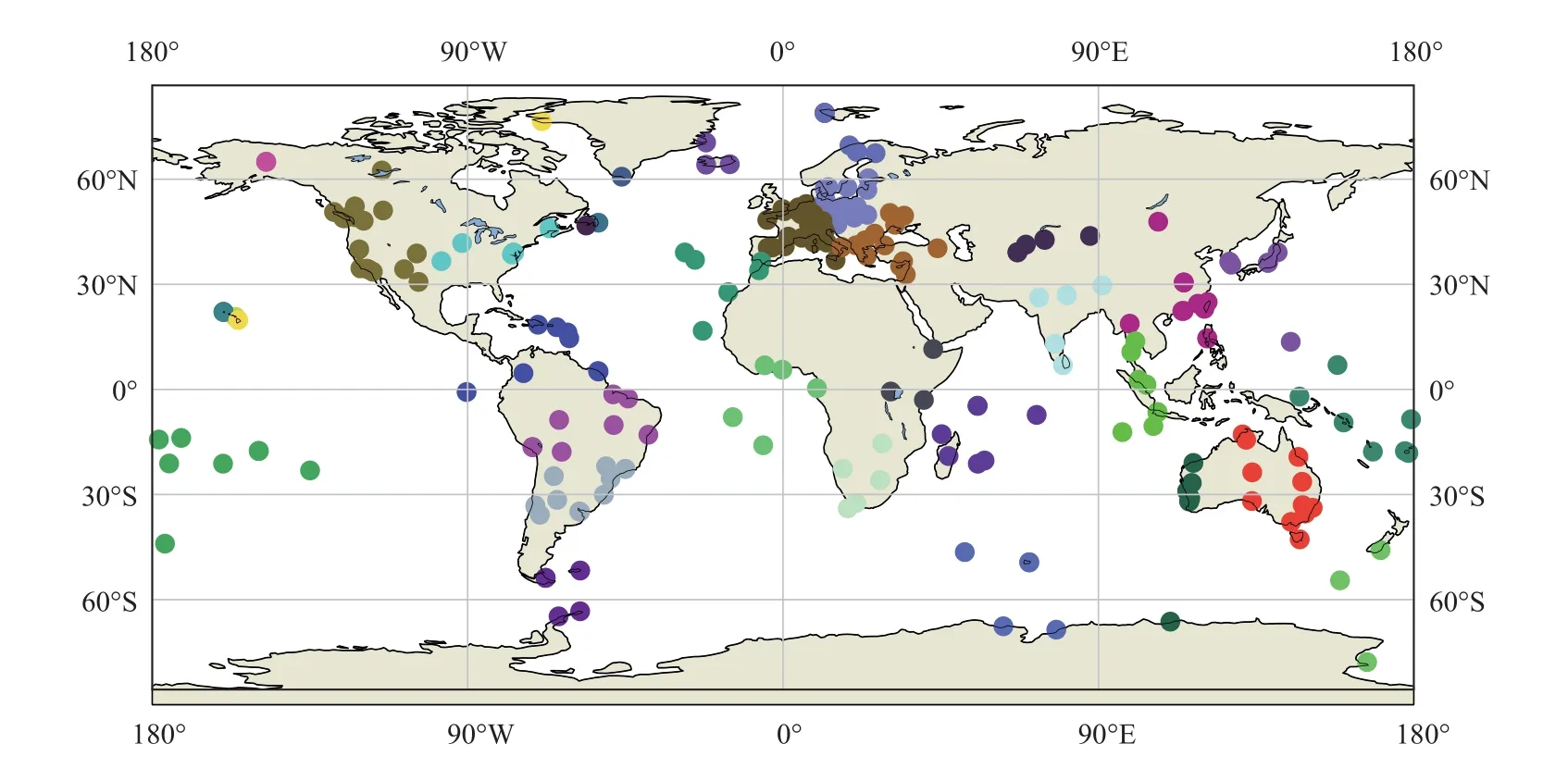
图1 K-means 算法对测站分类效果图
2.2 误差处理流程
由观测模型可知,GNSS 数据处理中涉及卫星端、接收机端、传播路径上等各类误差,需要充分考虑相关误差处理和模型改正.如信号传播过程中会受到地球引力场引起的时空曲率影响,相对论效应也会对卫星的时钟标称频率产生影响[7],文献[11]提供了相关改正公式.同样,天线相位中心偏差(PCO)、相位缠绕和潮汐改正(包括地球固体潮、海潮和极潮)等影响也需要通过相关模型进行改正[1].
对流层延迟改正模型函数为[12]
式中:mh、mw和mg分别为静力学、湿延迟和水平延迟梯度的映射函数;Dzh为天顶静力学延迟(ZHD);Dzw为天顶湿延迟(ZWD)[13];e为俯仰角;a为方位角;GN和GE分别为北、东分量的水平延迟梯度.在GNSS 处理中,ZHD 建模较充分,用模型给定初值即可;而ZWD 模型改正不足,需要对各个测站的剩余ZWD参数进行估计[14].
GNSS 信号受电离层影响,会产生测距误差,电离层延迟产生的测距误差是卫星导航中不可忽略的重要误差[15-16].电离层延迟误差一般包括一阶项和其他高阶项误差,文献[17]对电离层改正进行了详细分析,并提出了高阶项误差的改正公式.IF 组合模型可以通过不同频点观测数据的线性组合消除一阶电离层误差[1];非差非组合不对观测值进行线性组合,通过最小二乘平差,对单个历元卫星和接收机所有伪距和相位观测的倾斜总电子含量(STEC)参数进行估计.而电离层函数的各项误差,均可表示为与STEC相关的函数[7].因此,通过第一次参数估计得到的STEC参数值在随后的迭代过程中可以直接参与电离层改正.同时,估计的电离层参数还可以为差分码偏差(DCB)估计提供观测量[1].
由于相位偏差的存在,模糊度参数不具备整数特性.本文通过设置相位偏差和整周模糊度参数[7],估计得到整周模糊度的浮点解,然后通过Lambda 方法[18]及改进的Lambda 方法[19]进行整周模糊度的固定.
2.3 数据处理流程
通过变分方程和相关模型对轨道进行预处理,地球重力场模型采用GOCO06s 模型,其他模型见表1,轨道弧段为24 h,采样率为60 s.通过估计初始状态和ECOM 模型(ECOM)参数,对轨道进行拟合处理.
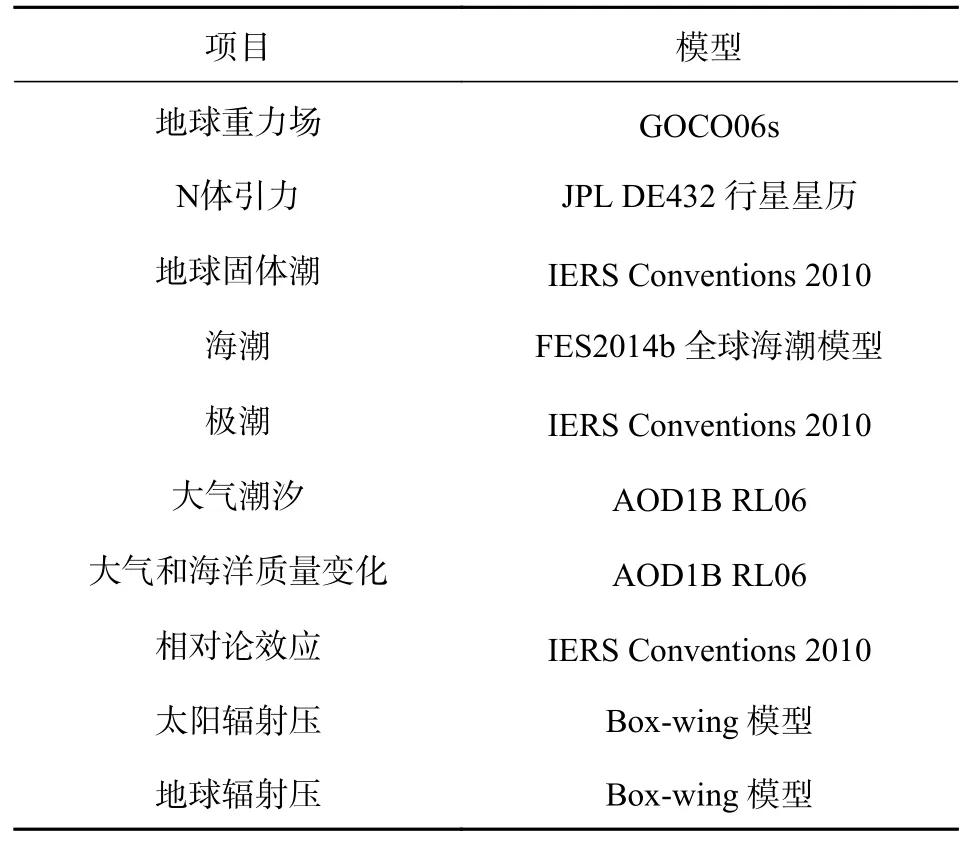
表1 轨道积分的力模型
观测数据通过MW 组合和GF 组合进行周跳探测,使用方差分量估计确定观测值权重.
测站坐标因地球非刚体形变而发生位移,因此,需要对其进行改正.根据国际地球自转服务(IERS)对地球固体潮、极潮建模,海潮通过全球海潮模型[20]建立.大气和海洋去混叠1B 级(AOD1B)06 版模型用于大气潮汐、大气和海洋质量变化建模[21].
最后,使用采样率为30 s 的IGS 观测站观测数据建立原始观测方程,使用参数估计方法进行迭代计算,最终获得收敛后的定轨结果.
3 实验与分析
为分析BDS-3 多频非差非组合精密定轨精度,验证K-means 算法测站选取的优势,实验选取可发射五频信号的BDS-3 MEO 和IGSO 共27 颗卫星,测站选取方案为:
方案1:根据人工经验选取测站(即通过以往进行精密定轨实验的经验,选取所需数量观测数据质量较好的测站);
方案2:通过K-means 算法选取测站.
频率选择方案为:
1)S1:B1I+B3I;
2)S2:B1C+B2a;
3)S3:B1I+B1C+B2a+B3I+B2b.
图2 和图3 分别为测站选取方案1 和方案2 使用的测站分布图,图中测站用红色三角表示.

图2 测站选取方案1 IGS 测站分布图

图3 测站选取方案2 IGS 测站分布图
实验定轨时段选取2022 年年积日第060—090共一个月的时间,将定轨结果与武汉大学IGS 分析中心的精密轨道产品进行对比.
3.1 多频A、C、R 三个方向RMS 月均值对比分析
通过统计实验数据,首先计算单个年积日中每颗卫星的A、C 和R 方向RMS 值,然后再计算每个年积日A、C 和R 方向所有卫星的RMS 均值,最终形成轨道精度对比图.
图4 为方案1 中每个年积日A、C、R 方向所有卫星的RMS 均值对比图.从图中可以看出,在多数时间内,S2 定轨精度要低于其他两个频率选择方案.通过进一步统计计算A、C、R 方向RMS月平均值,可知,S1 定轨结果中A、C、R 方向RMS 月均值分别为0.052 m、0.044 m、0.044 m;S2 定轨结果中A、C、R 方向RMS 月均值分别为0.055 m、0.048 m、0.047 m;S3 定轨结果中A、C、R 方向RMS 月均值分别为0.052 m、0.044 m、0.044 m.从统计结果可以看出,S1 和S3 A、C、R 方向RMS 月均值相较于S2,精度均提升约0.003 m、0.004 m 和0.003 m.
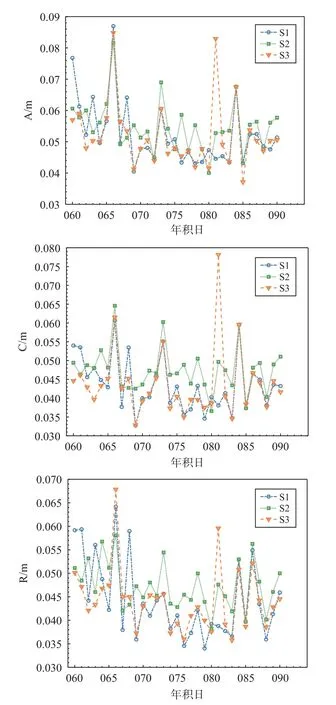
图4 方案1 中A、C、R 方向单天RMS 月均值
图5 为方案2 中每天在A、C、R 方向上所有卫星RMS 月均值对比图.同样,通过进一步统计计算三个方向RMS月平均值,可知,方案2 的S1 定轨结果中A、C、R 方向RMS 月均值分别为0.045m、0.038 m、0.039 m;S2 定轨结果中A、C、R 方向RMS 月均值分别为0.047 m、0.040 m、0.039 m;S3 定轨结果中A、C、R 方向RMS 月均值分别为0.046 m、0.039 m、0.040 m.可以看出,三种频率选择方案的定轨精度基本一致,而相较于方案1,定轨精度整体都有提升.
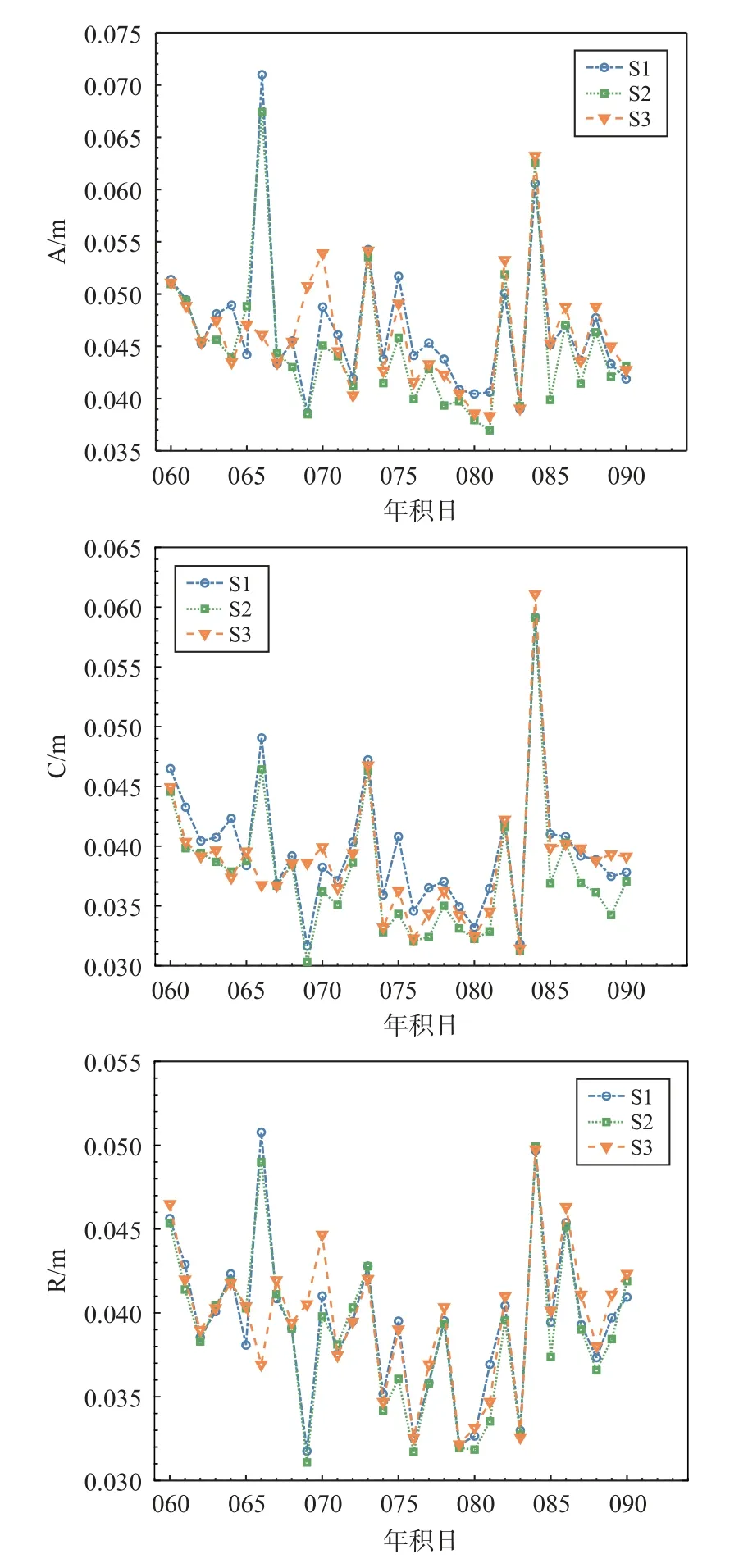
图5 方案2 中A、C、R 方向单天RMS 均值
3.2 3D RMS 月均值对比分析
通过计算得到每颗卫星每天的3D RMS 值,然后计算月均值并进行对比.
图6 为三种频率选择下两种测站选取方案中BDS-3 MEO 和IGSO 卫星的3D RMS 月均值对比.可以看出,两种方案的MEO 和IGSO 定轨精度中,方案2 的3D RMS 月均值除S2 中C38、C39 和S3中C38 卫星外,其他均低于方案1,很明显,方案2 的定轨精度更高.

图6 不同方案不同频率下的3D RMS 月均值对比
表2 和表3 详细统计了两种方案中每颗卫星不同频率选择的3D RMS 月均值和所有卫星的总体均值.从表2 可以看出,方案1 定轨结果中MEO 卫星3D RMS 月均值最小值为0.057 m、最大值为0.100 m,IGSO 卫星3D RMS 月均值最小值为0.127 m、最大值为0.219 m.从表3 可以看出,方案2 定轨结果中MEO 卫星3D RMS 月均值最小值为0.045 m、最大值为0.093 m,IGSO 卫星的3D RMS 月均值最小值为0.118 m、最大值为0.213 m.可以看出MEO 和IGSO 卫星定轨结果中方案2 的定轨精度相比于方案1 有一定提升.
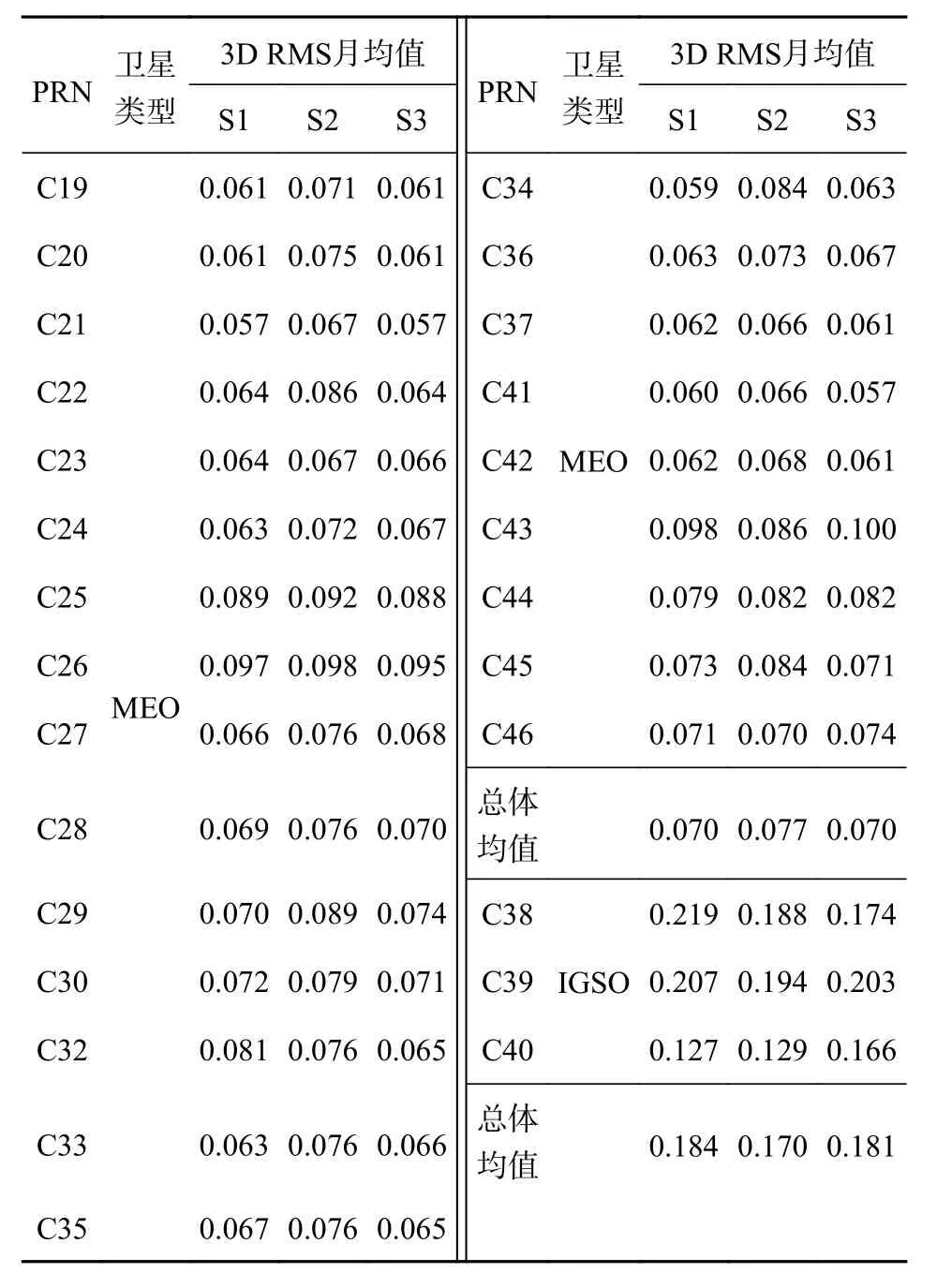
表2 方案1 不同频率选择方案的3D RMS 月均值 m
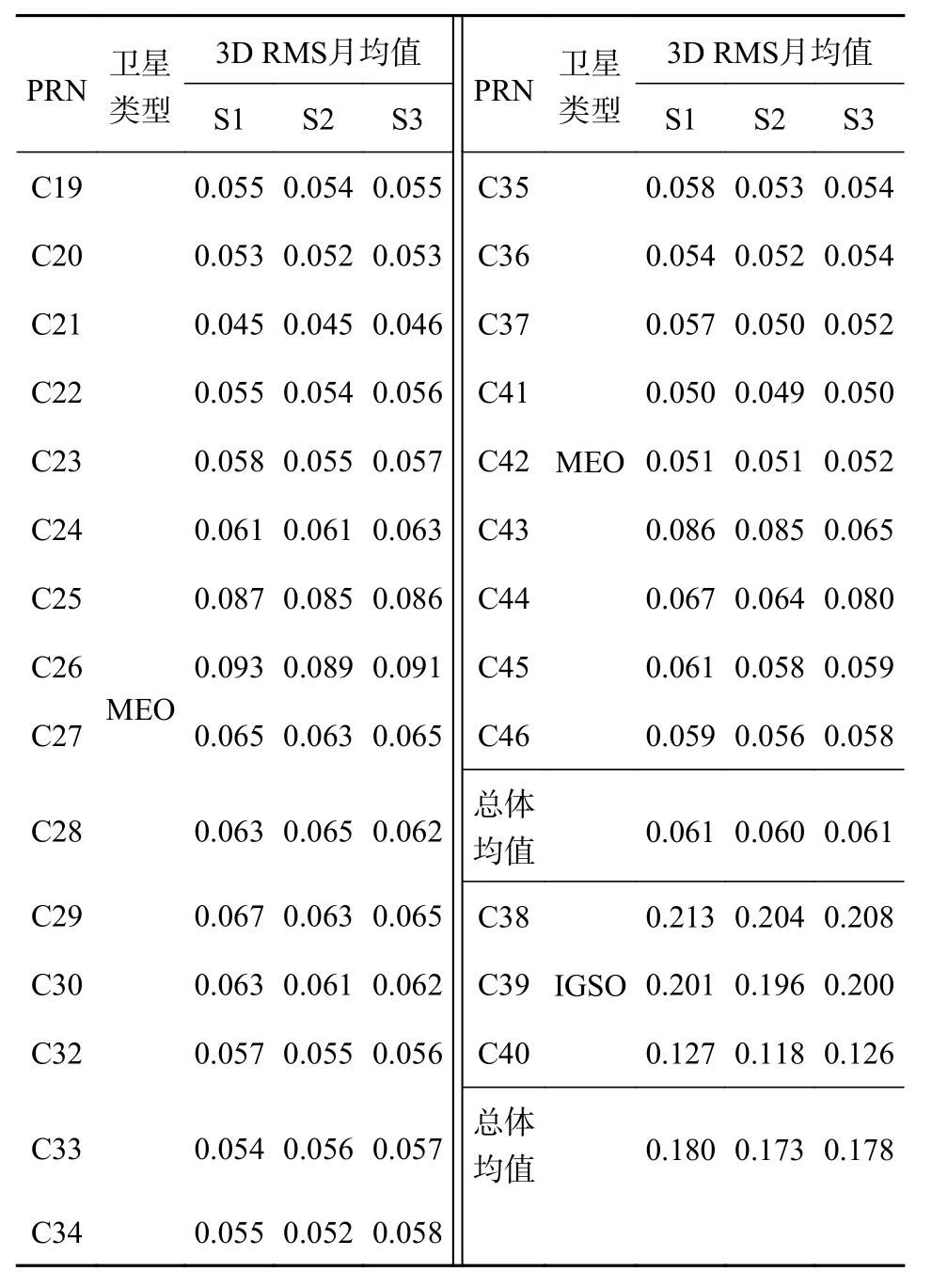
表3 方案2 不同频率选择方案的3D RMS 月均值 m
通过表2 和表3 对比MEO 和IGSO 所有卫星的3D RMS 月均值可以看出:方案1 中S2 大部分卫星3D RMS 月均值相较于S1 和S3 精度均偏高,其中MEO 卫星总体均值为0.077 m;而其他两种频率选择方案的月均值均为0.070 m,相差0.007 m.非差非组合方法通过纳入更多观测数据使精度提升约9.1%.与A、C、R 方向RMS 值对比结果一致,选用非差非组合方法利用更多频点观测数据进行精密定轨,能够提高定轨精度.
三种频率选择下,MEO 3D RMS 方案1 均值分别为0.070 m、0.077 m、0.070 m,方案2均值分别为0.061 m、0.060 m、0.061 m,IGSO 3D RMS 方案1 均值分别为0.184 m、0.170 m、0.181 m,方案2 均值分别为0.180 m、0.173 m、0.178 m.通过对比可以发现,本文提出的K-means 算法测站选取策略,所得定轨精度与人工经验选取方法相比,MEO 卫星在S1、S2 和S3 频率选择下,精度分别提升0.009 m、0.017 m 和0.009 m,而IGSO 卫星的定轨精度基本一致,各有优劣.分析认为,由于IGSO 卫星轨道的特殊性,覆盖范围为区域覆盖,其他区域的测站不能接收到IGSO 的观测信号,虽然方案2 的测站选取相较于方案1 有明显的优化,但是对于IGSO 卫星的测站布局并没有改善,两种方案对比中接收IGSO卫星信号的测站数量和布局没有明显优势,因此其定轨精度相当.可知,优化全球测站分布的方法对IGSO 卫星精度提升不明显.因其区域性的特点,需要采用中国境内或区域跟踪站优化测站布局改善IGSO 卫星定轨精度[22].
从表3 中的MEO 和IGSO 卫星3D RMS 月均值可以看出,S2 的定轨精度均高于其他两种频率选择方案,3D RMS 月均值提升约1 mm.初步推断,在测站分布较为合理,观测数据充足的情况下,优先选择新体制信号进行精密定轨即能得到较好的定轨结果.
3.3 非差非组合精密定轨优势讨论
表4 为不同测站选择方案中,各频率选择方案测站使用数量统计,其中,方案1 和方案2 可用de测站数量均为29 个,支持B1C+B2a 信号的测站分别为20 和27 个.

表4 测站使用数量统计
从表4 可以看出,方案1 中,接收S2 频点的测站相比S1 和S3 使用数量较少,导致测站分布几何构型较差,对比定轨结果,S2 定轨精度较低,而S1 和S3 定轨精度基本一致;方案2 中,S2 使用测站数量相比S1 和S3 减少两个,三种方案定轨精度基本一致.分析认为,方案1 中,在不确定所选测站是否支持所选频率的情况下,非差非组合方法纳入了更多频点观测数据,提高了测站使用数量,获得了更优化的测站几何布局,提高了定轨精度.对比方案1 中S1 和S3 以及方案2 的定轨结果,当测站数量相同,测站分布一致、几何构型合理的情况下,纳入更多频点观测数据对定轨精度提升不明显.通过对比同种频率选择、不同测站选取方案的定轨精度,方案2 定轨精度整体优于方案1,因此,测站几何构型相比测站数量和观测数据数量,对定轨精度的提升贡献更大.
从以上对比分析可以看出,影响定轨精度的主要因素为测站数量和测站几何观测信息,而测站几何观测信息对定轨精度影响最大.非差非组合方法使用更多频点观测数据,通过提高测站使用数量、优化测站几何观测信息,从而提高定轨精度.
非差非组合方法相较于IF 组合方法的定轨精度对比中,文献[23]对Galileo 双频、三频IF 组合和非差非组合的定轨精度进行了评估,两种定轨精度差异在1 mm 内;文献[1]示例性地给出了部分GPS 和Galileo 卫星两种定轨模型的定轨结果,结果显示定轨精度基本相当;文献[8]评定了GPS、Galileo 和BDS-2 的三频观测量对定轨结果的贡献,结果表明第3 频点观测量对精密定轨贡献很小,IF 组合和非差非组合的定轨精度结果基本一致.
在两种定轨模型结果基本一致的情况下,IF 组合通过不同频点观测值线性组合,消除电离层一阶项误差,会丢失观测值中的一些可用信息,并且放大了观测值的噪声[1].与IF 组合相比,虽然非差非组合方法增加了待估参数数量,但是在以下四方面具有明显优势:1)模型扩展性强,更加容易纳入多频点观测数据,充分利用BDS-3 多频资源;2)对电离层参数进行估计,获得电离层信息,可以进行电离层建模与反演研究;3)根据电离层信息,估计DCB,进一步估计观测量的码偏差(OSB)值,提供丰富的多频相关产品;4)避免IF 组合中放大观测噪声的问题.
通过实验分析,引入更多频点观测数据,虽然定轨精度提高存在局限性,但是对于OSB 估计、电离层建模等问题具有优势,在计算高精度轨道产品的同时,能够为用户提供更加丰富的多频点OSB 等产品.因此,在多频数据时代,非差非组合模型优势更加明显.
图7 显示了通过非差非组合方法利用五频观测数据,估计得到的BDS-3 2022 年年积日第060—091 伪距OSB 序列.伪距OSB 估计与DCB 相关,因此其特性与DCB 一致.可以看出,BDS-3 伪距OSB序列十分稳定,所有码类型中,C33 卫星伪距OSB 值较大.同一频率、不同码类型的伪距OSB 数值比较接近,如C1D 和C1P,而不同频率观测值的伪距OSB相差较大.
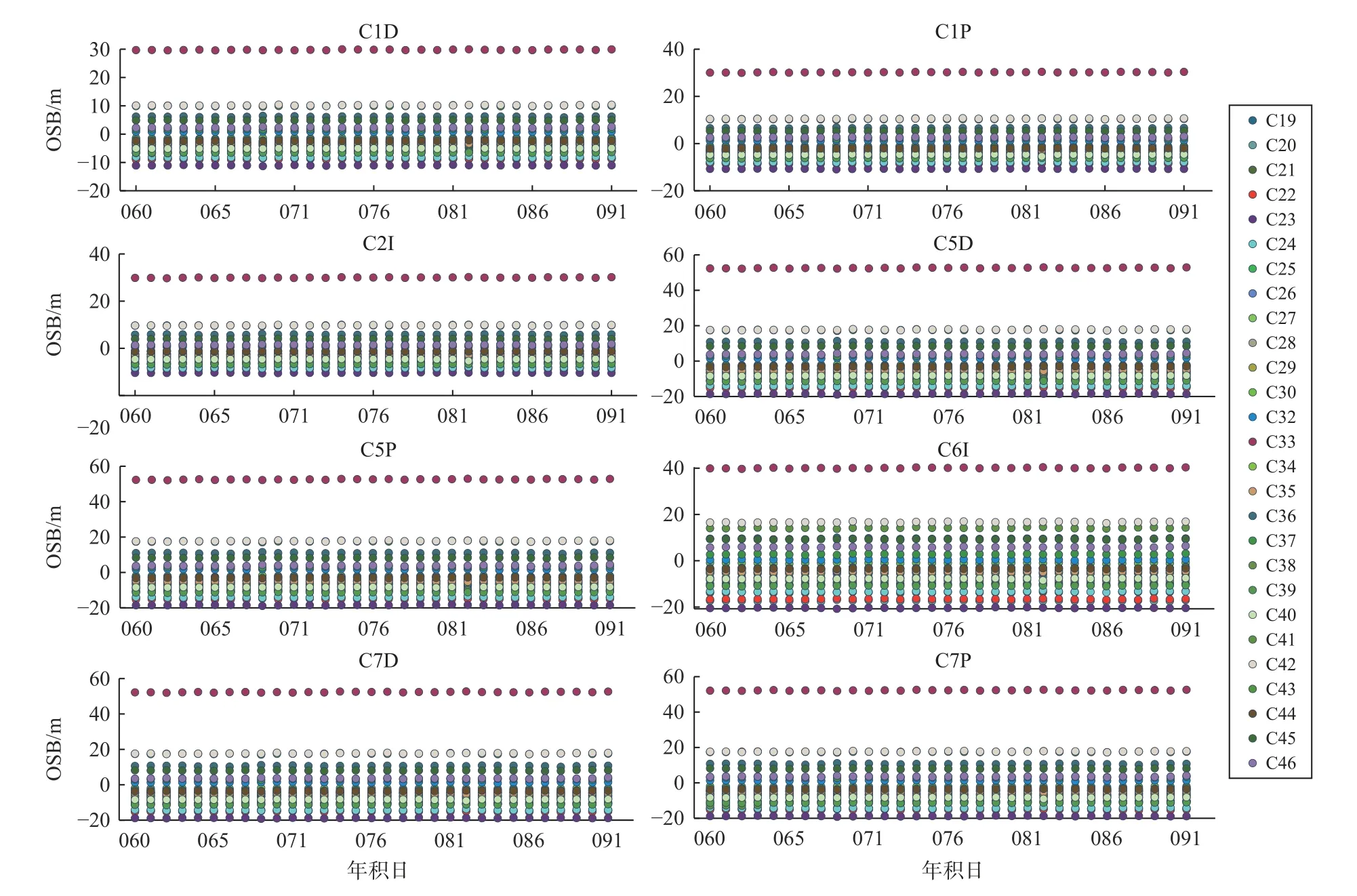
图7 BDS-3 卫星伪距OSB 估计值
4 结论
本文介绍了非差非组合方法的观测模型和参数估计方法,提出了通过K-means 算法进行测站选取方法策略.在此基础上,通过不同测站选取方案和频率选择方案,对BDS-3 MEO 和IGSO 共27 颗卫星进行了精密定轨处理,通过以武汉大学IGS 分析中心精密轨道产品为基准,以A、C、R 三方向RMS 月均值和3D RMS 月均值为指标,对定轨精度进行了分析,得出如下结论:
1)选取测站进行精密定轨时,可能存在测站不接收所选频点观测数据的情况,此时,非差非组合方法可以通过纳入更多频点观测数据提高定轨精度.
2)K-means 算法测站选取策略,能够提供分布更加均匀的测站,可以得到更好的定轨结果.当观测数据达到一定数量、测站分布又相同时,加入更多频点的观测数据对定轨精度提升不明显.
3)非差非组合方法灵活性高、可扩展性强,可以充分利用多频观测数据,在电离层特性研究、全频点OSB 估计等方面具有明显优势.
致谢:感谢iGMAS 分析中心(LSN)提供的硬件支持和技术帮助.感谢IGS 分析中心提供的数据支持.感谢Graz University of Technology 提供的软件支持.

