小波去噪与北斗三频信号周跳探测与修复
蔡巍,陈明剑,周舒涵
(中国人民解放军战略支援部队信息工程大学,郑州 450001)
0 引言
随着我国北斗卫星导航系统(BDS)的发展,对高精度定位的完整性、连续性和准确性的研究变得越来越重要.在BDS 精密定位中,跟踪BDS 信号的载波相位时,如果在特定的观察间隔内失去锁相,则所得的观察结果与之前和之后的观察结果相比,可能会出现不连续性,这种不连续性被称为小周跳,其严重影响导航和定位的准确性和可靠性.周跳检测和修复是实现系统高精度定位的有效途径之一,目前已开发了许多周跳检测和修复的方法.多项式拟合法适用于静态数据的周跳检测,但它易受观测噪声的随机性影响,因此对小周跳的检测并不理想,当周跳在多个时期多次发生时,检测效果也会变差[1].电离层残差组合方法可以检测到小的周跳,但存在检测结果多值的问题,无法准确地检测和修复周跳[2].Melbourne-Wübeena(MW)组合方法具有实时功能,但它无法检测具有相同系数的组合的周跳[3].为了克服MW 组合方法的缺点,提出了TurboEdit 方法.该方法将MW组合法与无几何相位组合法相结合,特别是用于非差和动态数据的周跳检测.然而,由于伪距的观测噪声,无法检测到小的周跳,上述方法主要适用于单频和双频数据.随着载波观测频数的增加,将三频甚至多频数据结合的组合系数进行周跳检测和修复已成为一种趋势.伪距相位组合和无几何距离组合(GF)是检测和修复周跳的典型三频方法.伪距相位组合方法可以快速检测周跳,但因含有伪距观测噪声的影响,难以检测到不敏感的小周跳.GF 组合方法可以探测小周跳,但是其组合系数矩阵的条件数很大,可能导致病态方程的发生.
针对上述方法的不足,本文首先对三频伪距相位组合采用小波去噪方法降低伪距观测噪声的影响[4],然后将三频伪距相位组合与三频GF 组合相结合,选择最优组合系数解决伪距相位组合的周跳检测不敏感和克服病态方程的问题;最后,通过最小二乘算法和正交三角(QR)分解算法相结合,固定周跳的最优整数并修复周跳.
1 伪距相位GF 组合模型及探测周跳原理
BDS 载波相位和伪距观测方程如下:式中:Pn和φn分别为BDS 第n频点的伪距和载波相位观测值,伪距观测值单位为m,载波相位观测值单位为周;ρ为卫星到接收机之间的几何距离,单位为m;c为真空中光的速度,单位为m/s;dtr和 dts分别为接收机和卫星的钟差,单位为s;为电离层的延迟系数,fn为第n个频点的频率;I1为频率f1的对应电离层延迟,单位为m;Trop为对流层延迟,单位为m;λn为BDS 第n频点信号的波长,单位为m;Nn为第n频点所对应的整周模糊度,单位为周;分别为载波相位和伪距观测值的观测噪声.BDS 具有播发三频信号功能,因此,选择B1I、B2I 和B3I 构成三频信号观测值组合进行实验,其信号频率如表1 所示.

表1 BDS 的三频信号参数
由式(1)~(2)可推导出三频伪距和载波相位的表达式:
式中:l、m、n为载波相位观测值组合的系数;下标a、b、c为三个频率伪距观测值组合的系数;Pabc为伪距组合测量值,单位为m;λlmn为载波相位组合观测值的波长,单位为m;εφlmn和εPabc分别为组合后的相位和伪距观测值的观测噪声;f1,f2,f3为信号的三种频率;Nlmn为组合后的整周模糊度,单位为周;φlmn为三频载波相位组合测量值,单位为周.
采样率越高,如1 Hz,电离层越平稳,相邻历元的电离层延迟变化越小.在这种情况下,可以忽略相邻历元的电离层延迟影响.用式(3)减去式(4),可以得到相邻历元的差分方程为
式中:Δ代表相邻历元间的差分;ΔNlmn表示无几何伪距组合的周跳估值,单位为周;伪距组合系数必须满足a+b+c=1和a2+b2+c2=min.GF 组合可表达为
式中,组合系数l、m、n必须满足l+m+n=0和(lλ1)2+(mλ2)2+(nλ3)2=min.对式(11)做历元间求差,可以得到GF 组合的周跳估值(单位为周):
假设BDS 三个频率的载波相位观测和伪距观测相互独立,根据文献[5-6]我们可以设置载波相位的噪声标准差δφ1=δφ2=δφ3=δφ=0.01周,伪距观测值的噪声标准差δP1=δP2=δP3=δP=0.3m,根据误差传播定律无几何伪距组合和GF 组合标准差分别为:
当组合观测值的周跳估值绝对值大于其均方根误差(RMSE)的4 倍时,置信度为99.9%,周跳可以认定为发生,其RMSE 的4 倍可以视为检测阀门值[7].当发生周跳时,.
为了更好地检测和修复不敏感周跳,选择了三个线性独立的组合,包括两个三频伪距相位组合和一个三频GF 组合.根据文献[8],相对于BDS 的B1I、B2I或B3I,无几何伪距相位组合的载波相位系数选择为(0,1,-1)和(1,4,-5),本文参考文献[9]中的无几何相位系数原则,选择(-1,1,0)作为GF 组合.
2 小波去噪原理
小波变换在信号局部特征的多尺度分析中具有优势.Daubechies 小波系统的db12 小波变换不仅可以消除噪声,而且具有较好的正则性和紧支集[10-12],可以保持信号的阶跃或突变点的位置不变.因此,db12 小波变换可用于对GNSS 伪距观测误差进行去噪,以提高周跳检测的性能.
假设P(t)为伪距信号的离散采样数据,使用db12 小波变换在不同的分辨率下分解,设C0,k=P(t),则分解公式为
式中:C为比例系数;对于伪距信号k为观测的历元数;下标j为分解的尺度;D为细节系数;n为滤波器长度;h和g分别为高频和低频滤波器.考虑到伪距信号的特点,本文选取j=1,即小波分解尺度为一层.
在含有噪声的原始信号中,无噪声的有用信号比较平稳,一般表现在原始信号的低频部分,而噪声信号表现在原始信号的高频部分.当对带噪声的原始信号进行小波变换时,小波系数相对于有用信号的最大范数将随着尺度增大,相对于噪声信号的最大范数会随着尺度的增大而变小.因此,有用信号和噪声信号小波系数通过小波变换可以清楚地区分.基于此原则,可以合理设置高频系数的阈值.阈值的选择和处理策略是小波去噪的关键步骤,Visushrink、SureShrink、Minimax 和BayesShrink阈值选择和处理策略是常用的方法[13].本文采用Visushrink 阈值确定方法,其表达式为
式中:MMAD为高频系数绝对值的中间数;N为信号长度.阈值消噪的过程中通常采用硬阈值消噪和软阈值消噪方法.软阈值函数具有良好的连续性和平滑性,但是所有的系数都被压缩了,导致信号的一些有效信息丢失.然而,硬阈值函数不会压缩信号的阶跃点或突变点,因此硬阈值处理策略被广泛用于去噪.硬阈值函数可以表示为
式中,Dj,k为小波系数,经过小波变换和去噪后的伪距观测值表达式为
3 实验分析
本次实验采用的是澳大利亚MTIS00AUS0 站点于2022 年1 月30 日采集的数据,采样间隔为1 s,其中BDS 选择C01 星的B1I、B2I 和B3I 信号作为实验对象,且信号均不含周跳和粗差.
3.1 无几何伪距相位小波去噪后性能
根据第2 节描述,考虑先使用小波阈值消噪对无几何伪距相位观测值进行处理,降低原始伪距观测值的噪声水平.图1(a)、(b)给出了消噪前的无几何伪距相位组合值,其中圆点表示使用未消噪的无几何伪距相位组合值得到的超宽巷模糊度N;图1(c)、(d)给出了消噪后的组合计算得到的超宽巷模糊度N,使用圆点标记各个历元的值.

图1 不同组合消噪前后得到的超宽巷模糊度N
由图1 可知:经过消噪处理后,混杂在有用信号中的噪声得到了大幅削弱,其中(0,-1,1)消噪后组合的超宽巷模糊度最大值为14.5188、最小值为14.444 8.而未消噪的超宽巷模糊度最大值为14.524、最小值为14.445 4;(1,4,-5)消噪后组合的超宽巷模糊度最大值为-68.654 2、最小值为-68.918 5,而未消噪的超宽巷模糊度最大值为-68.656 4;最小值为-68.923 7.消噪后波动幅度低于消噪前波动幅度,(0,-1,1)组合消噪前模糊度波动最大为0.078 6,消噪后模糊度波动最大为0.074;(1,4,-5)组合消噪前模糊度波动最大为0.267 3,消噪后模糊度波动最大为0.264 3.
3.2 无几何伪距相位周跳探测性能
在无周跳的情况下,由图2(a)、(b)可知,两个无几何伪距相位组合中的(0,-1,1)组合周跳探测量的波动均保持在[-0.03,0.03],(1,4,-5)组合周跳探测量的波动均保持在[-0.15,0.15].由图2(c)可知,GF 组合(-1,1,0)周跳探测量的波动均保持在[-0.003,0.003].
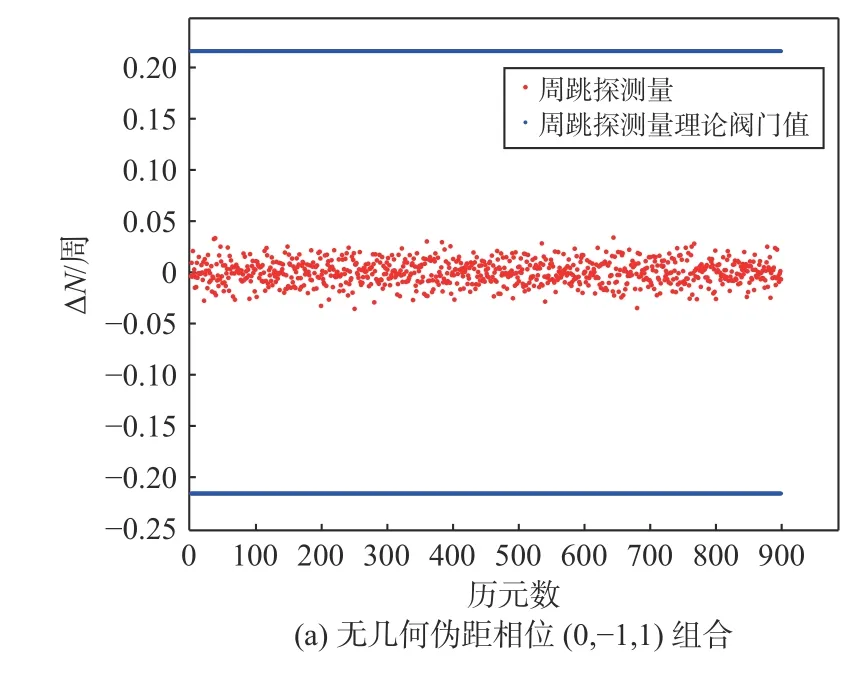
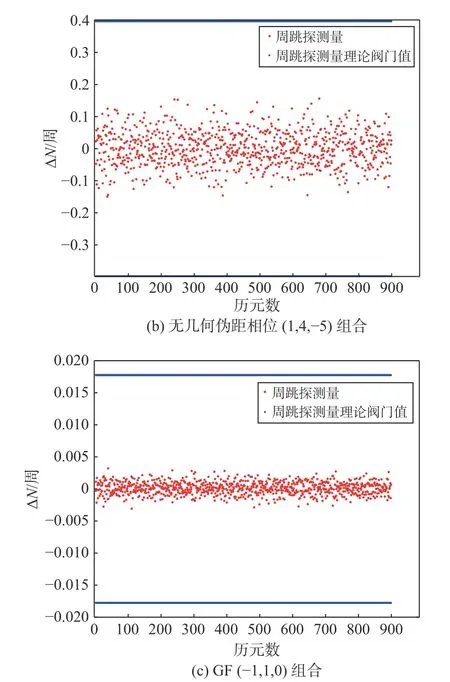
图2 不同组合在无周跳下的探测量
由此可知,相较于伪距相位组合,GF 组合的周跳探测能力更高,这是因为GF 组合比无几何伪距相位组合受到的噪声影响更小.
原始数据不含周跳,为了测试组合的周跳探测能力,本文分别在第50、99、149、199、299、399、499 七个历元中分别加入(1,0,0)、(0,1,0)、(0,0,1)、(1,1,1)、(5,4,4)、(2,2,2)、(14,14,15)周跳值,这些人为加入的周跳值有小周跳、大周跳、不敏感周跳和特殊周跳,用来验证本文所选线性组合的周跳探测及修复能力,图3 显示了三种组合观测模型的探测周跳能力,超出蓝色阀值线的红点为各历元产生的周跳.

图3 不同组合在有周跳情况下的探测量
由图3(a)可知,伪距相位组合中的(0,-1,1)组合可以探测出(0,1,0)、(0,0,1)和(14,14,15)这三种周跳值;由图3(b)可知,伪距相位组合中的(1,4,-5)组合可以探测出(1,0,0)、(0,1,0)、(0,0,1)、(5,4,4)和(14,14,15)这五种周跳值;由图3(c)可以看出GF 组合(-1,1,0)可以探测出(1,0,0)、(0,1,0)、(1,1,1)、(5,4,4)、(2,2,2)和(14,14,15)这六种周跳值.综合起来,将无几何伪距相位组合与GF 组合结合起来具有探测小周跳、大周跳、不敏感周跳和特殊周跳的能力,极大地减少了探测盲区.
3.3 周跳探测修复
当载波相位观测值中的周跳被成功探测出后,需要利用最小二乘算法对周跳进行修复,通过两个不同无几何伪距相位组合的系数和一个GF 组合的系数,形成最小二乘中系数矩阵A,X为三个频点上待求的周跳浮点解,而L为三个组合在各历元上的周跳探测量,由式(10)、(12)中的ΔNlmn和ΔNc构成.其表达形式如下:
理论上根据式(19),可以从周跳的浮点解X直接四舍五入得到周跳的整数解,由于系数矩阵中部分元素值较小,周跳探测量L发生微小的变化会造成方程求解产生较大误差变化,这就形成了病态方程组.为了得到更稳定的解,本文对系数矩阵A采取QR 分解,并且在浮点解法确定周跳修复值初值的基础上,利用空间搜索和L1 范数最小原理进一步搜索确定,其表达式为
具体周跳探测量和周跳修复结果如表2 所示.
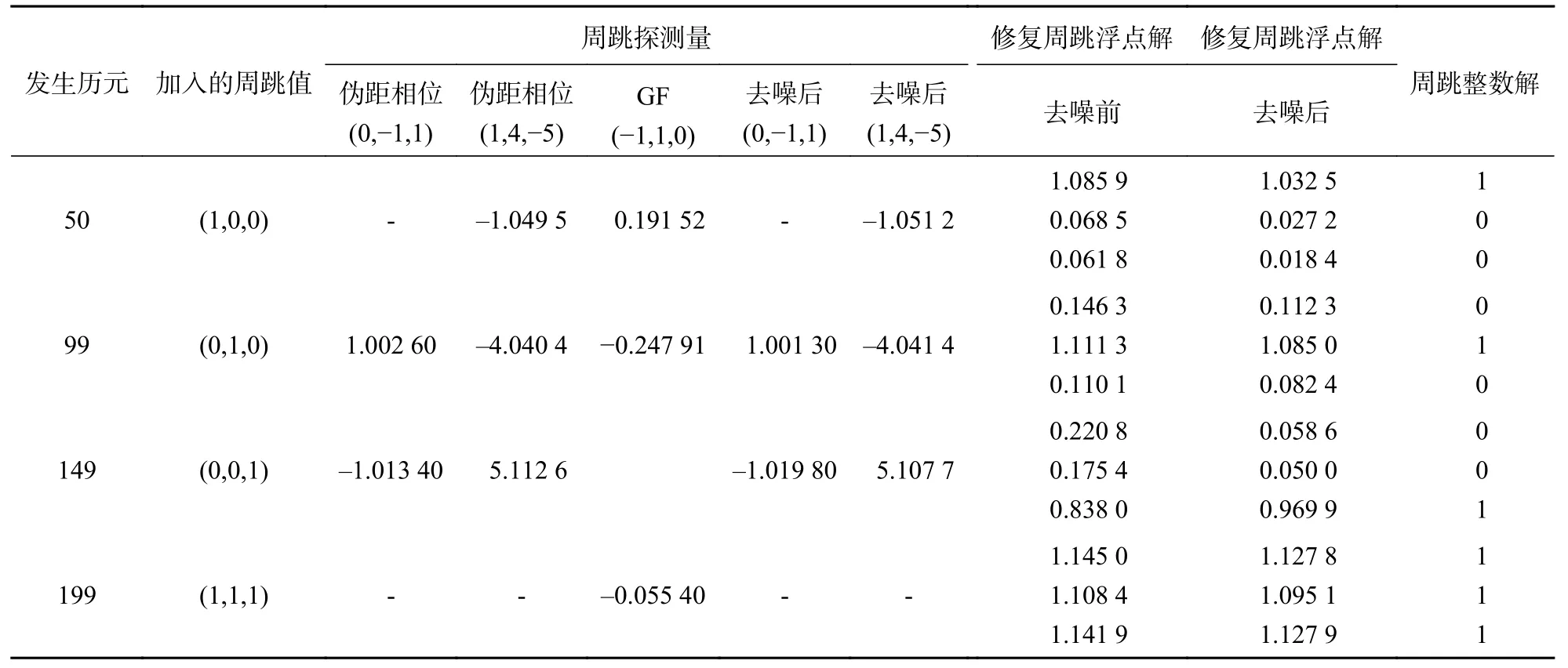
表2 各组合的周跳探测量与GFPMP-GF 组合在去噪前后周跳修复结果
由表2 可知,三种组合联合进行周跳探测可以覆盖所有类型的周跳,周跳浮点解和真实的整数解之间的差值可以用来反映观测值的噪声情况,噪声越大,浮点解与真实的整数值之间的差值就越大.去噪后,浮点解与真实值之间的差值最大为0.127 9、最小为0.018 4、平均为0.077 0;未去噪时,浮点解与真实值之间的差值最大为0.336 7、最小为0.054 6、平均为0.147 2.由表2 可知,不管去噪还是未去噪,本文提出的算法均能正确地修复周跳,但通过浮点解和真实值之间的差值比较,采用小波变换去噪后,大大地提高了周跳的探测与修复性能.
4 结论
针对BDS 的三频信号探测与修复周跳问题,本文提出一种基于小波变换去噪的方法,将无几何伪距相位与GF 组合模型,并利用真实的北斗数据进行实验验证后果表明,小波变换去噪的方法可以降低伪距噪声对无几何伪距相位组合模型周跳探测和修复的影响,去噪后的无几何伪距与GF 相结合提高了组合模型周跳探测与修复的性能,可以探测并修复各类型周跳.

