基于GNSS 实时数据流的载波相位差分测速方法及精度评估
胡冰燕,吕黄晖,郑佳伟,方荣新
(1.武汉大学测绘学院,武汉 430079;2.武汉大学卫星导航定位技术研究中心,武汉 430079)
0 引言
地震、火山、滑坡和泥石流等地质灾害给人类生命与财产安全带来了严重的危害,如何快速、准确地对地质灾害进行监测及预警是防灾减灾的重要手段之一.全球卫星导航系统(GNSS)具有全天候、全时段和高精度的优点,成为监测、预警滑坡[1]和地震[2]等地质灾害的重要技术.
地质灾害监测中的GNSS 高精度数据处理主要采用实时动态(RTK)和精密单点定位(PPP)方法[3].RTK 技术通过消除接收机钟差、削弱电离层和对流层延迟等误差影响,可达到厘米甚至毫米级的精度[3].在实际应用过程中,RTK 的定位精度会随着基线长度的增加而降低,并且在大范围的地质灾害监测(如地震监测)中存在稳定基准站选取困难的问题[1].PPP 利用精密轨道钟差产品可实现单站厘米甚至毫米级定位[4],但是存在收敛时间长、数据中断需要重新收敛等问题[1].
近年来,有学者提出了一种历元间载波相位差分测速的数据处理方法,仅利用广播星历即可达到mm/s 量级的测速精度.借助相邻历元间观测值差分,消除了载波相位的整周模糊度参数,显著削弱了电离层延迟和对流层延迟.有学者[5-7]对该方法进行了精度评估,王甫红等[5]采用静态数据模拟动态测速实验得到其精度可达到mm/s 级,在动态测速实验中,得到其精度可达到cm/s 量级.闫勇伟等[7]用北斗实测数据验证了方法的正确性,并得到在静态条件下北斗载波相位历元间差分精度可达mm/s级,在动态条件下测速结果精度可达cm/s级.同时,已经有学者将该方法应用于地震监测[8-10].但是以上研究大多是事后的仿实时模式,而对于实时监测应用,必须基于实时数据流进行测速.
基于此,本文提出基于GNSS 实时数据流的历元间载波相位差分测速方法,通过实时解码国际海运事业无线电技术委员会(RTCM)数据流,获取高频GNSS 广播星历(轨道和时钟)数据流传输,通过高频数据历元间差分,实现静态精度mm/s 级、动态精度cm/s 级的GNSS 测速.
1 方法
1.1 RTCM 解码
为满足高精度的GNSS 系统差分定位需求,RTCM提出了RTCM 协议.目前通用的RTCM 3.2 为最新版本,其增加的多信号电文组(MSM)可以支持多频多系统的GNSS,首次兼容了中国北斗卫星导航系统(BDS).RTCM 3.2 版本采用开放式系统互联参考模型(OSI),包含应用层、表示层、传输层、数据链路层和物理层5 个层面.表示层和传输层是RTCM编码和解码的关键,表示层规定了整个数据结构,包含数据要素、消息类型等;传输层定义了信息框架结构、传输协议和校验方式,为提高编码和解码的效率采用二进制位形式进行数据传输[11].
RTCM 3.2 一帧为一条标准的电文,包含5 个部分,如表1 所示,MSM 对应于电文结构中的“可变长度消息”.表2 中由于应用场景不同将MSM 分为MSM1~MSM7 7 类消息类型,其观测值内容依次增多,精度也依次升高[12].所有MSM 都由电文头、卫星数据和信号数据3 部分组成,如表3 所示[11,13].

表1 RTCM3.2 版本电文框架结构
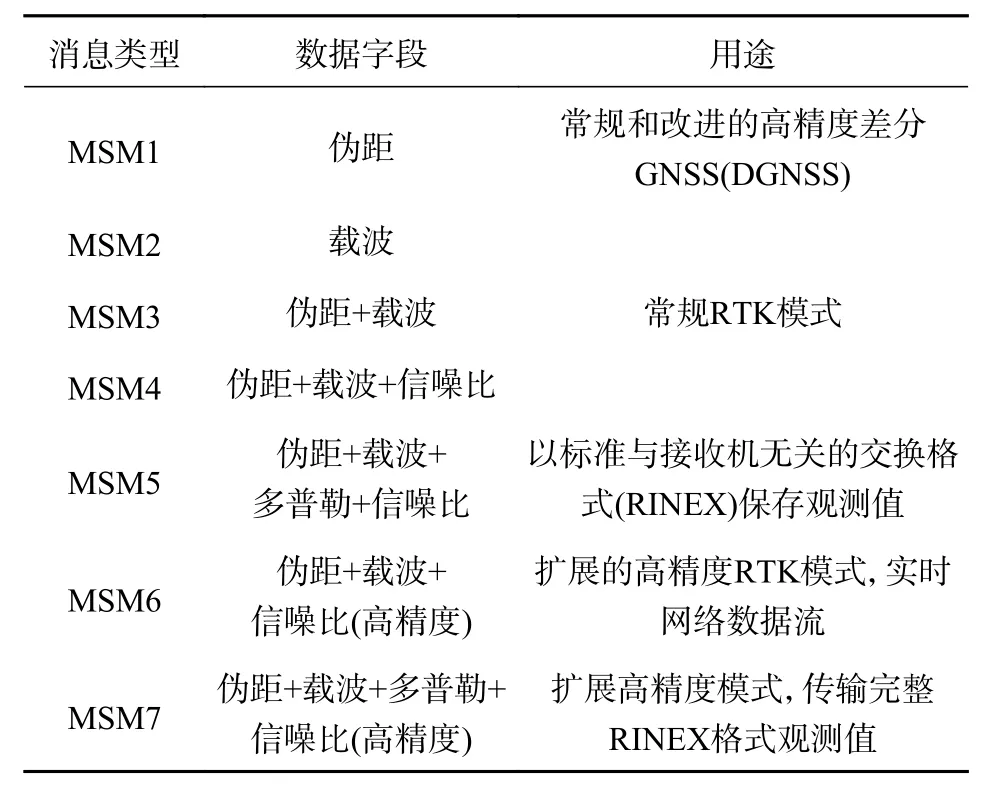
表2 RTCM3.2 版本MSM 消息用途及长度计算

表3 MSM 电文结构
有别于之前的RTCM 3.X 格式,RTCM 3.2 采用内部循环的方式来储存数据:循环编码各颗卫星的数据及其对应的信号数据.同时为了避免混淆,RTCM 3.2 规定每个系统均有对应的MSM 电文.
在逐帧进行RTCM 3.2 二进制数据解码时,首先判断开头8 位是否为引导字,若不是,则处理下一帧数据;若是,继续判断下6 位是否为0,如果判断为0,则根据下10 位得到信息长度.接着判断余下字节是否满足一条完整电文的长度,若满足,则读取一定长度字节计算循环校验码(CRC),并与给出的校验码进行比较,不同则放弃,处理下一帧数据;相同则通过校验,开始进行MSM 数据解码,按照MSM 电文结构,解码出相应数据.
1.2 载波相位历元差分测速模型
GNSS 在k历元内的非差载波相位观测值表达式为
式中:λ为载波的波长;φ为载波相位观测值;为卫星与测站之间的距离,s为卫星,r为测站,k为当前观测历元;c为真空中的光速;δtr,k和分别为测站接收机钟差和卫星接收机钟差;T和I分别为对流层延迟和电离层延迟;ε为多路径误差,包括载波相位观测噪声,以及模型改正后的大气延迟等无法模型化的综合误差.
将式(1)在接收机初始概略坐标X0,k=(X0,k,Y0,k,Z0,k)T处线性化为
假定两个相邻历元k、k-1间不存在周跳,对载波相位历元观测值求差可得
式中,Δ表示历元间差分算子.历元间差分削弱了电离层延迟误差和对流层误差,而且消除了载波相位的整周模糊度参数N.而对于高频(1 Hz 或更高)的GNSS 观测数据,在相邻历元间大气延迟和天线相位中心偏差等误差变化很小,可以忽略不计.于是式(3)可简化为式(4):
式(4)为GNSS 历元间载波相位差分测速法的观测方程,历元间接收机位置变化量ΔδXk,k-1和接收机钟差变化量Δδtr,k,k-1是待定参数.
假定测站接收机观测到n颗GNSS 卫星,则误差方程可表示如下:
式中,上标1,2,···,n为卫星序号.当卫星数量n≥4时,可以使用最小二乘法估计待定参数,进一步可求得历元间平均速度:
式中:V和X分别表示历元间平均速度和位移;Δt表示历元间时间间隔.
1.3 实时GNSS 测速流程
本研究采用的实时GNSS 测速程序主要分为三个部分:初始化,RTCM 解码,计算历元间差分测速.该程序首先实时接收RTCM 的数据流,同时设置基准站坐标、更新导航数据,同步实时输入流;接着开始逐帧处理缓冲区数据,进行RTCM 语句解码,储存广播星历和观测数据;然后开始历元间差分测速的计算,通过历元间载波相位求差,求接收机位置及钟差变化量,接着由此求历元间平均速度;最后判断数据流是否计算完成,未计算完成则进行下一组数据流的计算,重复以上步骤,计算完成则结束程序.实时GNSS测速流程如图1 所示.
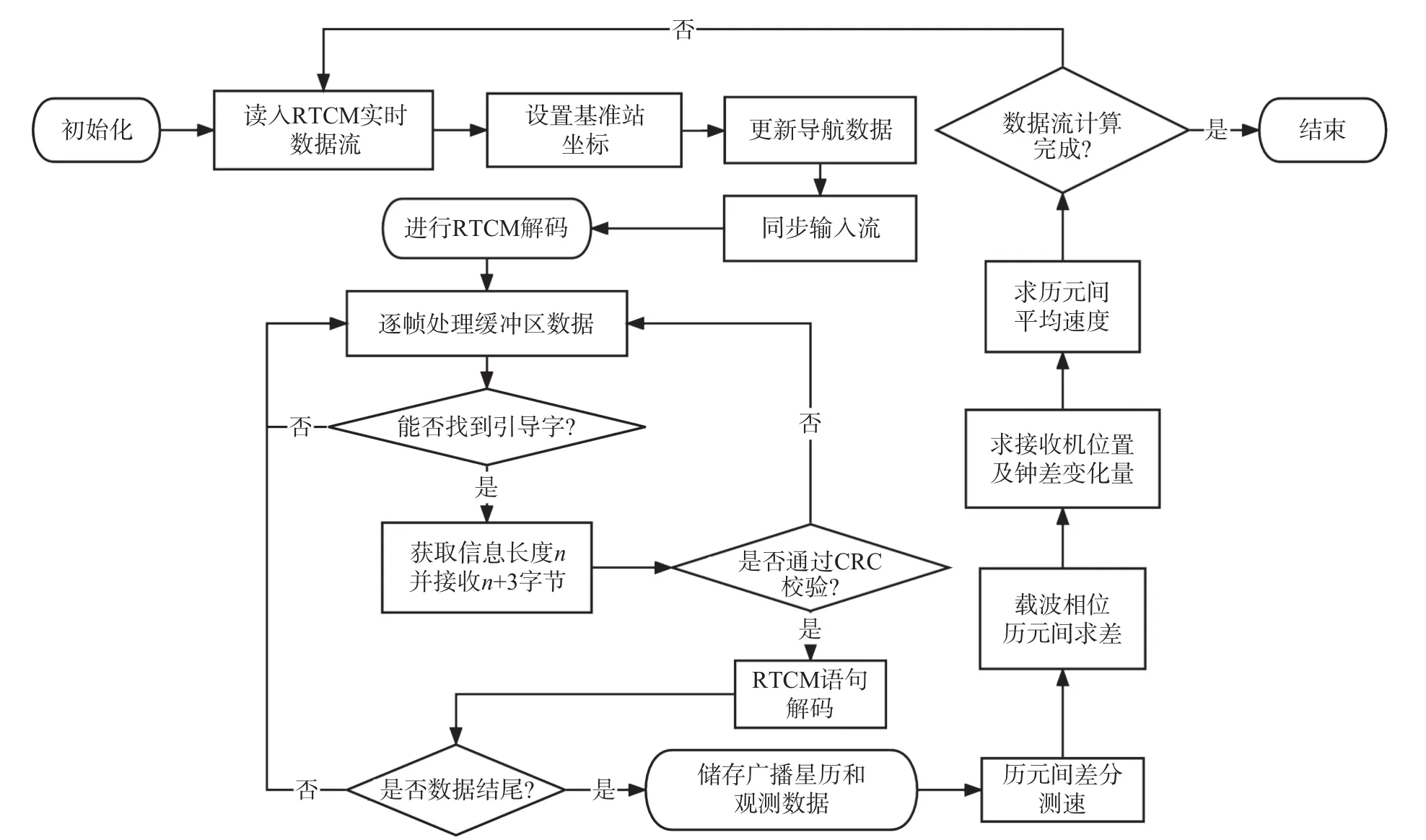
图1 GNSS 实时测速程序流程图
2 实验结果与分析
2.1 静态实验与精度评估
为了评估实验采用的实时GNSS 测速程序的静态测速精度,本文利用国际GNSS 服务(IGS)发布的实时数据流数据进行计算.选取2023-01-12T 16:00:02—18:00:02 LT ALGO、NRC1、FRDN、MAC1、CEDU 5 个静态测站实时接收到的GNSS 观测数据,5 个测站分布如图2 所示,测站位置信息如表4 所示.
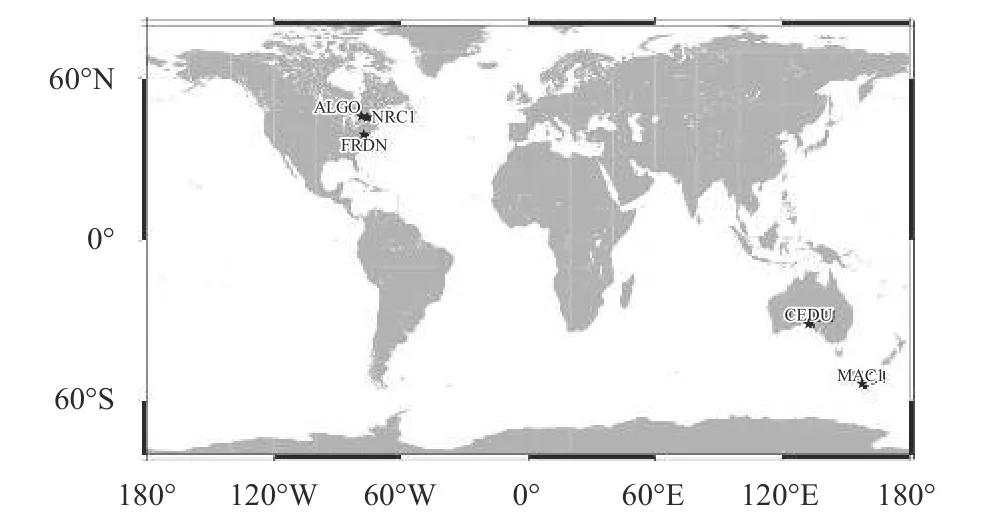
图2 测站分布图
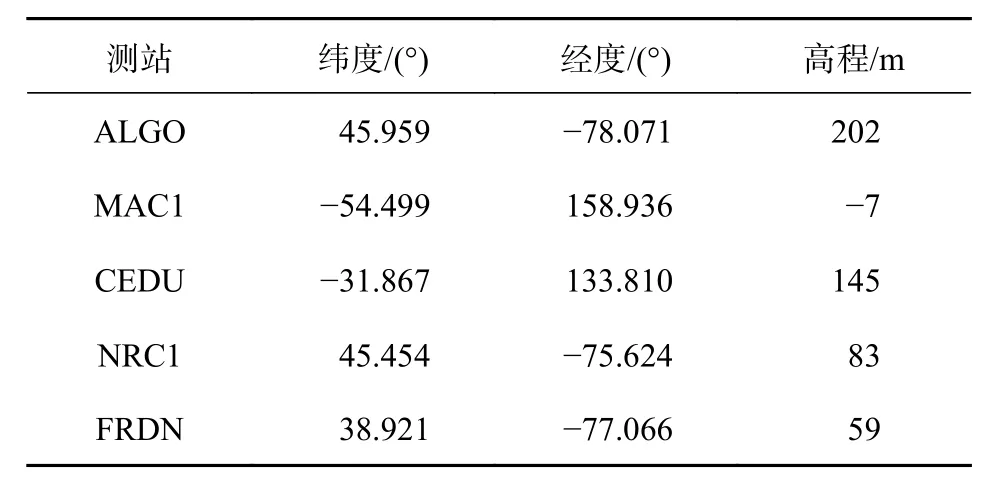
表4 测站位置信息
表5 利用图1 程序对各测站的观测数据进行测速解算,分别统计各测站东(E)、北(N)、天顶(U)三个方向速度的均方根(RMS),结果如表5 所示.
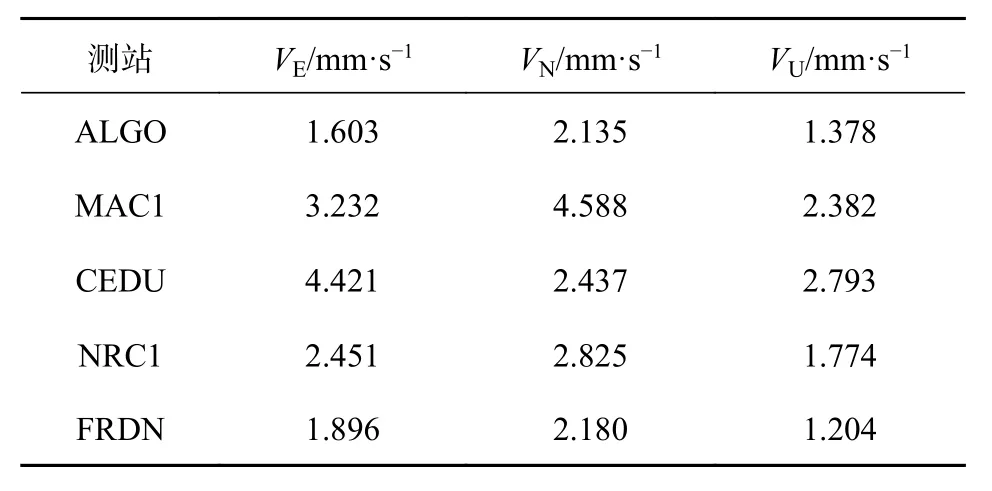
表5 所有测站测速结果的RMS
由表5 可知,图1 测速程序对5 个测站E、N、U 三个方向的测速结果的RMS 都在5 mm/s 以内.
为更加清晰且全面地展示该GNSS 实时测速程序的静态站测速的效果,图3 给出了测站ALGO 在2 h内的测速结果.可以看出,虽然整体的测速结果略有波动,但是E、N、U 三个方向的测速结果几乎都稳定在10 mm/s 以内,相较于静态站E、N、U 三个方向速度真值(均为0 m/s),该程序对静态站测速结果的精度可以达到mm/s 级,相较于伪距差分测速cm/s级的精度有所提高,达到了PPP 测速的精度.

图3 ALGO 测站2 h 内的测速结果
2.2 动态实验与精度评估
为了对该GNSS 实时测速程序的动态精度进行评估,使用振动台来模拟正弦波振动.所采用振动台由加拿大Quanser 公司生产,型号为Shake Table II.该振动台为单轴振动台,台面大小为46 cm×46 cm,最大行程±7.6 cm,最大振动频率为10 Hz,2.5 g 加速度下的最大载荷为7.5 kg.振动台上安装有嵌入式编码器,可以从3µm 的精度记录振动台位移,数据采样率高达2 000 Hz.
振动台实验于2021-03-27 下午在武汉大学教学实验大楼楼顶进行.振动实验平台被牢固地安装在地面上,振动平台上固定的GNSS 天线(Trimble Zephyr geodetic model 2)随着振动平台的振动而运动,采用的Trimble Alloy 接收机以20 Hz 的采样率记录数据.振动实验平台的设置如图4 所示.

图4 振动实验平台
同时,还进行了PPP 的位移解算,以便将PPP 位移结果与实时GNSS 程序测速结果积分得到的位移以及振动台的位移真值进行对比,进一步分析实时GNSS 测速程序的测速精度.
动态实验采用振动台模拟振动频率为0.5 Hz、振幅为3 cm 的正弦波,GNSS 数据采样率为5 Hz.程序测速结果和振动台速度真值的结果如图5 所示,可以直观看出该程序的测速结果与真值无论是在波形还是在幅度上的符合度都是非常高的.但是由于观测数据具有偶然误差,导致程序的测速结果在波峰和波谷时与真值略有不符.为了更严谨地进行精度评估,将该程序测速结果和振动台速度真值作差,求得RMS为10.4 mm/s,说明该GNSS 实时测速程序动态测速结果的精度可达cm/s级.

图5 GNSS 实时测速结果与振动台真值比较
为进一步评估该GNSS 实时测速程序动态测速的精度,将程序的测速结果进行积分得到位移,与0.5 Hz/3 cm 的振动台位移真值和PPP 位移结果对比分析结果,如图6 所示.可以观察到,三组位移值十分接近.为定量评估位移结果的精度,将程序测速积分的位移结果、PPP 位移结果分别与振动台位移真值作差,计算得到RMS 分别为5.1 mm 和6.6 mm,说明该GNSS 实时测速程序结果积分得到的位移相较于PPP 位移结果和振动台真值更为接近.
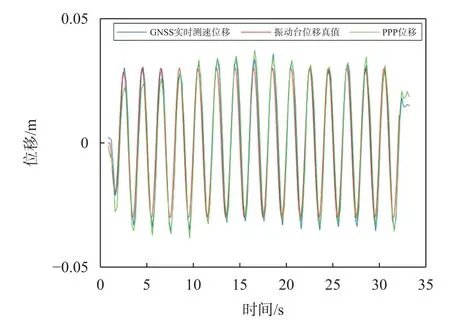
图6 GNSS 实时测速结果、振动台真值、PPP 位移结果比较
3 结束语
本文通过对传统的GNSS 载波相位差分测速程序进行改进,增加实时接收数据流模块进行RTCM 解码,以满足实时数据进行测速的需求.利用静态站的数据和振动台模拟正弦波振动输出数据,分别进行静态实验和动态实验以完成改进后的GNSS 实时测速程序的精度评估.实验结果表明,采用静态站实时流数据解算时,N、E、U 三个方向的误差都在5 mm/s 以内;振动台模拟正弦波的动态实验中,与振动台输出真值的差值RMS 为10.4 mm/s.说明该程序在静态实时测速条件下的测速精度可达mm/s 级,在实时动态测速的条件下仍能达到cm/s 级的精度.

