星地时间比对大气误差修正及其影响因素分析

王荣，白燕，赵家奇，郭燕铭，陈晓锋

(1.中国科学院国家授时中心,西安 710600；2.中国科学院大学,北京 100049；3.哈尔滨工业大学(深圳)空间科学与应用技术研究院,广东 深圳 518000)

0 引言

随着原子钟技术的发展，近年来，利用空间环境实现高精度时间频率基准已成为各大国研究的热点.例如欧洲空间局开展的ACES 计划；我国的载人航天空间站也部署建设了空间站时频柜项目，拟在空间站建立不确定度在10-18～10-19量级的空间时间频率基准[1,2].

高精度时间频率基准的应用需要精度与之相匹配的时频传递技术作为支撑，星地时间比对是实现精密时间传递的重要技术手段[3].目前常用的星地时间比对法有激光时间比对法、单向时间比对法及双向时间比对法.星地激光时间比对法可实现百皮秒量级的时间比对精度[4]，但是由于激光传播过程中，受云雾、降雨等因素影响较大，其可靠性不强[5]，且不能全天候工作.星地单向时间比对法[6-7]受电离层、对流层及轨道等的影响较大，因此其时间比对精度较低.而星地双向时间比对法由于其具有授时精度高、实时性好、受环境影响小等特点，近年来已成为全球范围内星地时间比对的重要手段.

利用双向测量的星地高精度时间比对算法能够消除大部分系统误差，然而由于星地上下行信号频点和路径的不同，导致对流层和电离层色散延迟无法通过作差完全消除，将在一定程度上影响最终的时间比对精度.因此如何消除星地时间比对过程中的大气色散时延是目前实现星地高精度时间比对中必须要解决的问题.

大气误差的修正可以分为对流层误差修正和电离层误差修正两个部分.当前常用的对流层误差修正方法为函数模型法[8]，常用的对流层误差修正模型有Hopfield 模型、Saastamoinen 模型和UNB 模型，但函数模型法只考虑了对流层非色散部分的误差，结合实测气象参数的模型其修正精度也只能达到亚纳秒级[9]，而皮秒级时间比对对于对流层色散误差会提出更多的要求.对于电离层误差，单频接收机需要通过导航电文中播发的电离层改正参数对电离层延迟进行改正，Klobuchar 模型、NeQuick 模型、低阶球谐模型等是卫星导航系统常用的单频接收机电离层误差修正模型，双频接收机可通过双频观测值对电离层误差进行修正.

针对搭载高性能原子钟组的低轨卫星和地面站之间实现高精度时间比对的需求，本文对星地时间比对链路中的电离层和对流层色散延迟修正方法展开研究，并对大气色散延迟修正的主要影响因素进行了仿真和探讨，可为星地高精度时间比对提供一定的技术积累.

1 星地时间比对原理

卫星与地面站之间通过持续互发互收测距信号实现卫星与地面站之间时间比对的方法称为星地双向时间比对.其基本原理是：地面站将上行测距信号进行相应的调制，然后通过天线将测距信号发射至卫星，卫星接收到地面站信号后，将测距信号解调，测量出地面站至卫星的上行测距值，并将此测量数据通过通信链路回传至地面站.同样，卫星也将下行测距信号发送至地面站，地面站也可获得卫星至地面站的下行测距值，地面数据处理中心收集上、下行测距数据，通过一定的算法修正链路中的各项误差，即可解算出星地钟差.双向测量方程为

式中：PSG和PGS分别为下行和上行测距数据；LSG和LGS为地面站与卫星间的几何距离；c为光速；xS和xG分别为卫星和地面站钟差；δion_SG和δion_GS分别为下行和上行链路中的电离层误差；δtro_SG和δtro_GS分别为下行和上行链路中的对流层误差；εSG和εGS为链路中的其他误差项.

在星地时间比对中，可将地面站原子钟时间作为基准时间，因此可认为地面站钟差xG=0，则卫星钟差即星地相对钟差.将式(1)中的两个式子作差，即可解算出星地相对钟差为

式中，Δd为由于上下行传播距离不一致引起的空间距离误差，可以通过高精度轨道信息进行修正[10]，本文不作详细介绍.本文重点对电离层和对流层误差的修正模型及其误差影响因素进行研究和分析.

2 双向时间比对中的大气误差及其修正方法

卫星与地面站之间在互发互收信号时，空间环境对信号的影响主要体现为大气对信号的影响，主要包括电离层延迟和对流层延迟.假定卫星向地面站发射下行信号的频点为f1，地面站向卫星发射上行信号的频点为f2，利用f1和f2的测量信号通过双向时差算法解算出星地相对钟差.同时，卫星向地面站通过频点f3发射另一路下行信号，利用f1和f3双下行信号辅助实现链路的电离层误差修正.

2.1 电离层误差修正

当无线电微波信号穿过电离层时，会受到电离层中电子的干扰，其传播的方向及速度均会发生改变.在本文的研究中，将利用f1、f3频点的两下行测距值作差求解出星地链路上的倾斜总电子含量(STEC)值，进而可求得链路上的电离层误差值.电离层误差模拟流程如图1 所示.

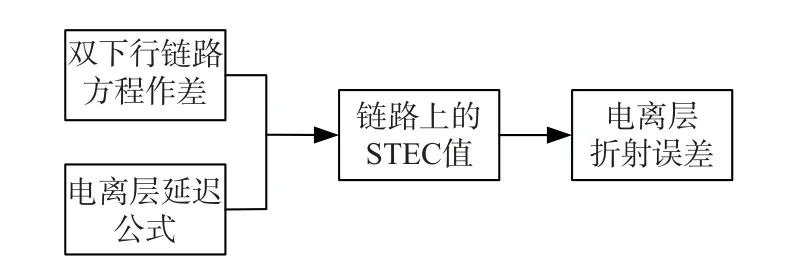
图1 电离层误差模拟流程图

频率为f的信号在电离层中的折射延迟为

式中：STEC 为信号传播路径上电离层电子密度的积分，即斜径电离层总电子含量；B0为电磁场强度；θ为地磁场的方向与电磁波信号传播方向之间的夹角；e为电子的电荷量；m为电子质量；ε0为真空介电常数；µ0为真空中的磁导率.由式(3)可知，当求出星地链路上的STEC 时，即可求出相应链路上的电离层延迟.

在本文所讨论的星地时间比对链路系统中，通过双下行链路(频率分别为f1、f3)方程作差可求解出对应链路上的STEC.假设双下行链路同时接收到测距信号，则双下行链路的观测方程为

式中：PSG1和PSG3分别为频率f1和f3的下行测距值；LSG1和LSG3为卫星和地面站的几何距离；xS和xG分别为卫星和地面站钟差；δion,1和δion,3分别为频率f1和f3的电离层误差；δtro,1和δtro,3分别为频率为f1和f3的对流层误差；εSG1和εSG3分别为频率为f1和f3的下行链路中的其他误差项.

将式(5)中的两式作差，可解算出两下行链路的电离层误差值之差：

式中：Δρ1,3为双频测距值之差；Δδtro将根据2.2 小节的对流层误差修正模型计算；Δε可根据相应的方法进行修正，这里将不再赘述.根据式(3)，下行频点f1和f3的电离层延迟分别为

由式(7)中的两个方程作差，可得

将式(6)中求得的 Δδion代入式(8)中可求得STEC 值.由于双下行链路路径几乎是一致的，且在地心地固坐标系下，上行链路与下行链路路径差别为空间站位置区别，位置差别仅为几米，可认为电离层几乎无变化，不足以影响时频比对的结果，因此可认为各链路对应的STEC 相同.

将式(8)中求得的STEC 带入式(3)，即可分别求得上行频点f1的电离层误差值和下行频点f2的电离层误差值：

将式(9)中的两式作差，即可求出上下行链路的电离层延迟之差：

2.2 对流层误差修正

当前对流层误差修正的常用方法为函数模型法，例如Hopfield 模型、Saastamoinen 模型、UNB 模型等.这些模型修正方法主要是针对对流层非色散误差进行修正.但随着原子钟技术的发展，在时间比对精度要求更高的系统中，则需要考虑对流层色散延迟[11].

在本文的研究中，将利用大气再分析数据计算对流层折射率，采用三维射线追踪技术得到各个频率在不同仰角、方位角情况下的对流层折射延迟，进而可得到双频对流层延迟差.对流层折射误差模拟流程图如图2 所示.

图2 对流层折射误差模拟流程图

计算对流层用到的大气再分析数据为网格气象数据，其中包含了温湿压数据，该数据的水平分辨率为0.25°×0.25°(经纬度)，其高度按照气压分层，从100～1 000 hPa，步长50 hPa，共19 层.

大气折射率可通过大气温湿压数据计算得到，对流层的折射率可表示为

式中：N0为非色散项；N′(f) 和N′′(f)为频率相关的复合折射率部分，在计算折射延迟时不需要考虑折射率虚部.在本文所讨论的双向时间比对系统中，可通过双向伪距差分消除非色散延迟.本节接下来将主要针对对流层色散延迟进行讨论.色散延迟的折射率N′(f)为

式中：Si为网格气象数据中第i线的强度，为氧气或水汽谱线的形状因子实部；将采用ITU-R P.676-12[2019]来计算Si和的值；是由气压造成的氮吸收产生的干燥空气连续吸收谱的实部；f为频率，单位GHz；pd为干压，单位hPa；；T为温度，单位K；g=5.6×10-4(p+e)·θ0.8，，ρ为水汽密度.

本文所讨论的三维射线追踪基于费马原理，即在两个气象格网点之间，计算最短路径作为微波信号的传播路径.在地心地固坐标系中，若卫星位置坐标为(x0,y0,z0)，地面站坐标为(xm,ym,zm)，微波信号在穿过对流层的过程中，共经过m个大气格网点到达地面站接收机，则可迭代计算出对流层传播时延：

式中，ni为式(13)中计算的折射率.则上下行链路的对流层延迟差为

将利用三维射线追踪算法计算得到的对流层折射延迟作为真值，供构建对流层折射修正模型用.对流层折射修正模型假设天顶方向的双频对流层色散延迟差为表面干压pd、水汽压pw，以及温度T的线性函数，同时利用映射函数将天顶方向投影至任意仰角，由于当仰角大于10°时，映射函数的精度几乎相同，因此采用简单的一阶近似，形为1/sinel，则上下行链路的对流层折射修正模型为

式中：el为仰角；pd、pw以及温度T通过地面设备测量得到；a为模型系数.

3 仿真试验及性能验证

先利用基于低轨卫星与地面站的星地高精度时间比对系统进行仿真得到下行f1和f3频点、上行f2频点的伪距测量值(f1≈30 GHz ,f2≈25 GHz ,f3≈20 GHz)，然后通过本文第2 节给出的大气误差修正方法对星地时间比对链路中的大气误差进行修正.由于信号传输过程中的大气误差会受到卫星姿态和轨道位置等相关因素的影响，因此我们考虑通过调整不同的误差参数设置仿真分析几种主要误差因素(姿态误差、相位中心标定误差、轨道位置误差)对大气误差修正的影响.

本文仿真所用到的大气数据为欧洲中期天气预报中心发布的2020 年1 月1 日的ERA5 数据.ERA5数据是由欧洲中期预报中心对实测气象数据的进一步整合得到的第五代大气再分析数据.借助中国科学院国家授时中心分析中心搭建的星地时间比对仿真应用平台生成一组低轨卫星的真实轨道(不带误差)，利用该轨道数据计算相应的大气误差，并将该组大气误差数据作为真值.然后将不同的姿态误差、相位中心标定误差和精密定轨误差组合叠加到轨道文件中，基于轨道计算相应信号路径下的大气误差.利用两组大气误差的差值及其均方根(RMS)表征大气误差修正方法的修正精度.

3.1 大气误差分析

3.1.1 卫星姿态误差对大气误差修正的影响

不同的姿态误差将影响卫星的位置，进而会对大气误差产生影响.当相位中心标定误差设置为1 mm、精密定轨误差设置为10 cm(噪声误差设置为0.2 cm)时，分别仿真当姿态误差为50 as、60 as、70 as、80 as、90 as、100 as 时的大气延迟修正情况，结果如图3所示.

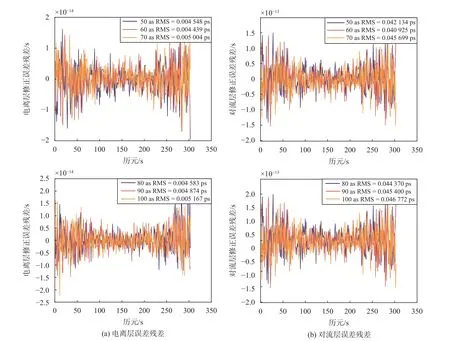
图3 不同姿态误差的大气误差残差

由图3 可看出，当相位中心标定误差设置为1 mm、精密定轨误差设置为10 cm(噪声误差设置为0.2 cm)时，将姿态误差由50 as 增大至100 as，采用本文提出的电离层、对流层误差修正方法，电离层误差残差的RMS 值小于0.006 ps，对流层残差的RMS值小于0.05 ps.

3.1.2 相位中心标定误差对大气误差修正的影响

不同的相位中心标定误差会影响空间站的位置坐标，进而会对大气误差产生影响，当卫星姿态误差设置为72 as、精密定轨误差设置为10 cm(噪声误差设置为0.2 cm)时，分别仿真当相位中心标定误差在0.5mm、1.0mm、1.5mm、2.0mm、3.0mm 以及5.0mm时的大气延迟修正情况，结果如图4 所示.

图4 不同相位中心标定误差的大气误差残差

由图4 可知，当卫星姿态误差设置为72 as、精密定轨误差设置为10 cm(噪声误差设置为0.2 cm)、将相位中心标定误差由0.5 mm 增大至5.0 mm 时，采用本文所述的电离层及对流层误差修正方法对大气误差进行修正，电离层误差残差的RMS 值小于0.006 ps，对流层误差残差的RMS 值小于0.06 ps.

3.1.3 精密定轨误差对大气误差修正的影响

在上文所述的大气误差修正方法中，轨道位置是一个重要的参量.精密定轨误差的精度也将影响大气误差的修正.精密定轨误差主要可分为两部分：一是系统误差部分，二是噪声误差部分.在本节的讨论中，均将精密定轨误差中的噪声误差百分比设为5%.当卫星姿态误差设置为72 as、相位中心标定误差设置为1 mm 时，分别仿真当精密定轨误差在2 cm、5 cm、10 cm、15 cm、20 cm 以及30 cm 时的大气延迟修正情况，结果如图5 所示.

图5 不同精密定轨误差的大气误差残差

由图5 可知，当卫星姿态误差设置为72 as、相位中心标定误差设置为1 mm，将精密定轨误差中噪声误差比例固定在5%，精密定轨误差从2 cm 增长至30 cm 时，采用本文所述的电离层及对流层误差修正方法对大气误差进行修正，电离层误差残差的RMS值小于0.005 ps，对流层误差的残差值小于0.05 ps.

3.1.4 综合各误差项对大气误差影响分析

综合考虑上述几种主要误差因素对大气误差的影响，仿真当姿态误差100as、相位中心标定误差5mm、精密定轨误差30 cm(噪声误差设置为0.2 cm)时的双向电离层误差、双向对流层误差，结果如图6 所示.

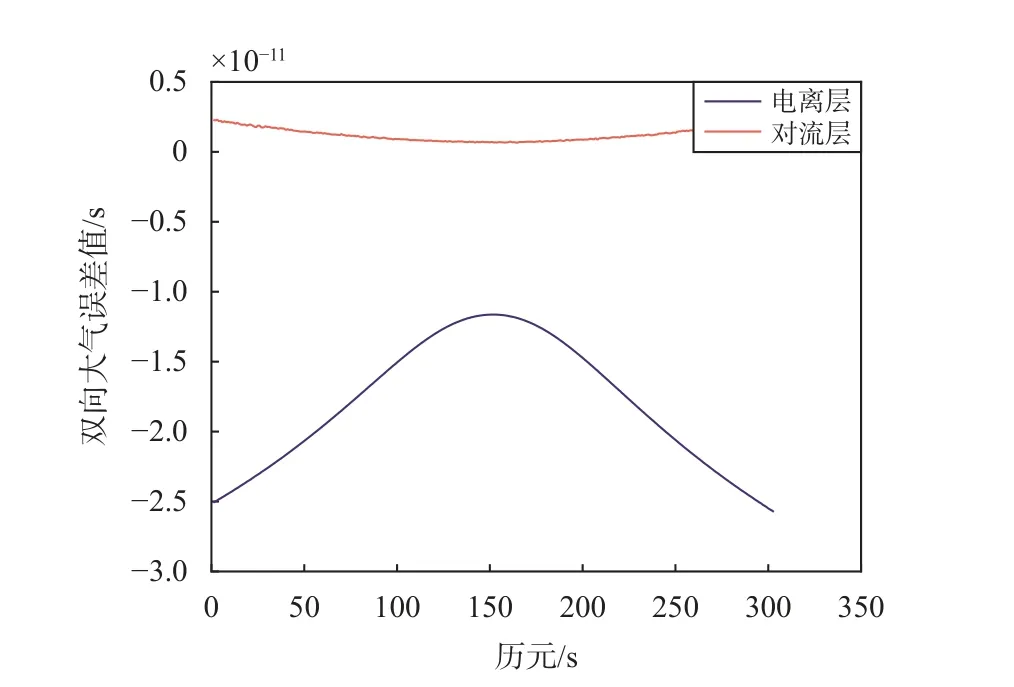
图6 双向大气误差

由图6 可知，当姿态误差为100 as、相位中心标定误差为5 mm、精密定轨误差30 cm(噪声误差设置为0.2 cm)时，经过双向时间比对差分后的双向电离层误差峰峰值大约为25.739 8 ps，双向对流层误差峰峰值约为2.379 9 ps.可见，在双向时间比对系统中，经双向伪距差分后，由于上下行信号路径不一致(时频设备所处轨道不一致)引起的大气误差能够抵消掉大部分，但残余的大气误差值对于皮秒级的时间比对系统仍然是不可忽视.为此，需要对双向残余大气误差作进一步修正.基于本文提出的大气误差修正方法，仿真姿态误差100 as、相位中心标定误差5 mm、精密定轨误差30 cm(噪声误差0.2 cm)时的大气误差修正，结果如图7所示.

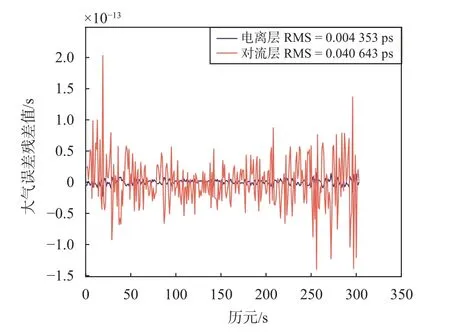
图7 大气修正误差

由图7 可知，大气修正误差值大致在10-13ps 量级，这说明经前文所述的方法修正后，残留的大气误差值已经很小了.本文星地时间比对系统的指标主要是针对其精度影响，因此经过修正后大气残余误差对于皮秒级的时间比对精度影响不大，是满足系统要求的.

3.2 星地时间比对性能分析

由3.1 节讨论可知，卫星姿态、轨道位置及天线相位中心标定等重要参数的精度对大气误差的修正结果会产生一定的影响，进而对基于双向测量体制的星地时间比对性能也产生相应的影响.分别改变不同参数值仿真计算不同场景下的钟差拟合残差，并用该拟合残差的RMS 值表征星地时间对比精度.

3.2.1 卫星姿态误差对星地时间比对精度的影响

不同的卫星姿态误差将影响轨道位置和速度，而钟差解算时，卫星位置和速度将影响星地时间比对链路中的部分误差项，如电离层、对流层误差等的修正，因此固定相位中心标定误差1 mm、精密定轨误差10 cm(随机分量0.2 cm)，则针对不同姿态误差下的双向时间比对结果如表1 所示.

表1 不同姿态误差下的星地时间比对精度

由表1 可知，随着姿态(欧拉角)误差的增大，50～100 as 姿态误差下的时间比对精度在0.21～0.22 ps 浮动，这对于当前皮秒级的时间比对精度是合理的.说明姿态误差在50～100 as 变化时，对最后的时间比对精度的影响并不大.

3.2.2 相位中心标定误差对星地时间比对精度的影响

不同相位中心标定误差会对轨道的实际位置造成影响，从而影响星地时间比对精度.固定卫星姿态误差72 as、精密定轨误差10 cm(随机分量0.2 cm)，则针对不同相位中心标定误差下的星地时间比对结果如表2 所示.

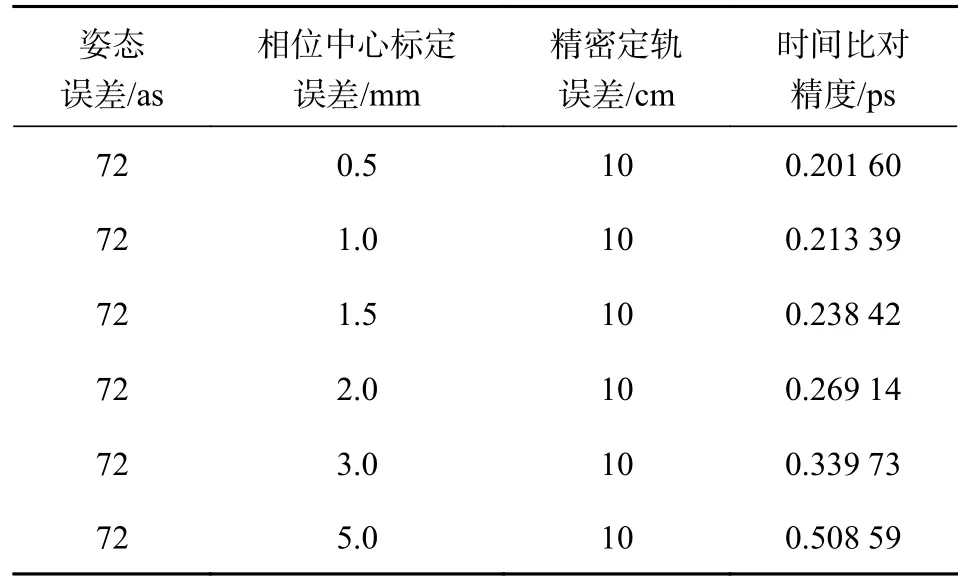
表2 不同相位中心标定误差下的星地时间比对精度

由表2 可知，相位中心标定误差在0.5～5 mm 的变化过程中，随着相位中心标定误差的增大，星地双向时间比对精度在逐渐降低，其影响在亚皮秒量级，对于皮秒级的时间比对精度应充分考虑其影响.

3.2.3 精密定轨误差对星地时间比对精度的影响

精密定轨误差会对星地双向时间比对精度产生一定的影响，该影响将直接反映到时间比对解算过程的空间距离、相对论效应、大气延迟等误差中.固定卫星姿态误差72 as、相位中心标定误差1 mm、将精密定轨误差中的噪声误差设为0.2 cm，分别仿真当精密定轨误差为2 cm、5 cm、10 cm、15 cm、20 cm、30 cm时的星地双向时间比对结果，同时仿真当卫星姿态误差为72 as、相位中心标定误差1 mm、精密定轨误差中的噪声误差为2 cm 时的星地时间比对结果，如表3所示.

表3 不同轨道位置误差下的星地时间比对精度

由表3 可知，当固定噪声误差为0.2 cm 不变，轨道位置误差从2～30 cm 变化的过程中，随着轨道位置误差的增大，星地双向时间比对精度在0.21～0.22 ps变化，对于当前皮秒级的时间比对精度是满足要求的.

为进一步分析精密定轨误差对星地时间比对精度的影响，当保持轨道位置误差为30 cm 不变，将其中的随机噪声误差由0.2 cm 增大至2 cm 时，时间比对精度从0.21 ps 变化至1.95 ps，变差了1.7 ps.因此，对于皮秒级的时间比对精度，应充分考虑随机噪声误差的影响.

综合考虑三种误差因素对星地时间比对精度的影响，仿真姿态误差为100 as、相位中心标定误差为5 mm、精密定轨误差为30 cm(噪声误差设置为0.2 cm)时的星地时间比对精度，结果如图8 所示.

图8 综合误差时的双向时间比对精度

由图8 可知，在卫星姿态误差100 as、相位中心标定误差5 mm、轨道位置误差30 cm(噪声误差设置为0.2 cm)的场景下，可以实现皮秒量级的星地时间比对精度.

在本文所讨论的星地高精度时间比对链路中，除大气误差外，还存在空间距离误差、周期性相对论误差、引力时延误差等，这些都会对星地时间比对精度产生一定的影响.

4 结论

本文研究了星地双向时间比对链路中的大气误差修正方法，利用仿真数据验证了星地双向时间比对链路中电离层和对流层误差的修正方法，分析了不同误差源对电离层和对流层误差修正的影响，通过本文的仿真和分析，可以得出：

1)当卫星姿态误差小于100 as、相位中心标定误差小于5 mm、精密定轨位置误差小于30 cm(噪声误差比例为5%)时，利用本文的大气误差修正算法修正后，电离层误差残差小于0.006 ps，对流层误差残差小于0.06 ps.

2)当精密定轨误差包含的随机噪声部分控制在2 cm 以内，则在卫星姿态误差100 as、相位中心标定误差5 mm、精密定轨误差30 cm 的场景下，均可以实现皮秒量级的星地时间比对精度.

3)基于本文仿真的各种场景，通过对卫星姿态、相位中心标定、精密定轨等误差在一定范围的调整，其对电离层误差修正的影响基本可控制在0.006 ps内，对对流层误差修正的影响可控制在0.06 ps 内，但对星地时间比对的精度仍可能会产生一定的影响.这主要是由于在星地比对链路中还存在空间距离不一致、相对论效应等误差.为了保证高精度的时间比对精度，其他各类误差的修正方法及综合应用将是后续进一步研究的重点.