基于PSO-Elman 神经网络BDS 导航卫星钟差预报

王井利，佟晓宇，张梅

(1.沈阳建筑大学交通与测绘工程学院,沈阳 110168；2.宣化科技职业学院,河北 张家口 075100)

0 引言

导航定位系统进行定位的关键是“时间”因素的测量.星载原子钟是星上时间基准，其与地面控制站的钟面差值即卫星钟差，钟差精度是影响其服务能力的重要因素之一[1].在全球多导航系统并存的情况下，我国自主研发了北斗卫星导航系统(BDS)，其卫星钟差预报的精度和稳定性备受关注.由国际GNSS服务(IGS)提供的精密钟差产品精度高,但是其产品的发布需要延迟12 至18天，无法用于实时定位[2].因此，如何提高短期钟差预报精度以满足实时定位的要求成为该类研究的重点[3].

目前，关于钟差预报建模的问题，国内外学者进行了相关研究，并取得了大量成果.钟差预报模型的种类有很多，常用的有二次多项式(QP)模型[4]、灰色(GM)模型[5]、附加周期项多项式(SA)模型[6]、小波神经网络(WNN)模型[7]、自回归滑动平均(ARMA)模型[8]等.由于星载原子钟的类型不同、受外在因素影响较大，不同的模型在钟差预报时预测结果具有差异，线性模型很难为不同类型的卫星提供高精度的预测结果.针对此类问题，文献[9]分析了北斗三号卫星导航系统(BDS-3)不同种类卫星钟的精度和稳定度，采用四种模型对不同原子钟下的精度进行比较，为BDS-3 钟差预报建模提供了有利的参考.文献[10]针对卫星钟差精细化建模问题，提出了将具有记忆反馈功能的Elman 神经网络用于钟差预报中，并验证了该想法的可行性；但是该模型在网络训练的过程中容易出现局部最优解的问题影响预测结果.文献[11]针对北斗钟差预报建模问题，提出一种依据单一模型均方误差经典线性加权进行多个模型组合预报的方法，解决了单一模型在不同情况下受干扰因素影响从而导致预测结果出现明显差异的问题；但是该方法模型权重设置为固定值，随着时间累计单一模型的误差累计对预报结果影响较大.文献[12]提出了一种能够实时拟合和将泛函网络和多项式结合预报钟差的方法，并通过实验验证了该方法精度的可靠性；但是其模型的参数选取依赖于人工经验，影响了预测精度.文献[13]针对传统预报模型的缺点，提出了一种基于北斗二号卫星导航系统(BDS-2)、BDS-3 联合估计的超快速卫星钟差预报优化策略；对分析中心北斗钟差产品精细化有重大意义；但是依据新策略建模提升的预测精度有限.

常用的传统预报模型受模型阶数、预测时长、钟差数据等因素影响较大，而神经网络结构不稳定、泛化能力差，容易出现过拟合导致局部最优.针对此类问题本文提出一种基于粒子群优化(PSO)算法优化Elman 神经网络的钟差预报模型来实现高精度的导航卫星钟差预报.

1 钟差数据预处理与三种传统预报模型

1.1 钟差数据的预处理

在武汉大学卫星导航定位技术研究中心(WHU)下载的精密钟差产品为卫星的相位数据，该类型数据呈整体递增或者递减的线性规律.原始卫星钟差相位数据可直接用于导航、定位和授时(PNT)服务，但相位数据的相对数量级较大，不利于钟跳、粗差等异常值的识别及剔除，因此需要对相位数据进行预处理工作[14].首先相位数据可以通过相邻历元做一次差转换为频率数据，转换后的频率数据整体呈非线性规律，容易探测出异常值.然后用相应的方法剔除不同异常值后再恢复成相位数据.完成预处理之后的相位数据用于钟差预报可有效提高钟差预报的精度.

本文采取的预处理流程为中位数偏差(MAD)抗差估计法探测异常值[15]，再采用分段线性插值的方法进行内插还原异常点.其中MAD 表达形式为

式中：yi为卫星频率数据；m为频率数据序列的中间数.

求得MAD 之后，将频率数据的中间数m与N倍的MAD 相加，然后与卫星的频率数据yi的绝对值相比较，从而探测出异常值的位置(本文N值取经验值3).

1.2 常用的三种传统预报模型

1.2.1 QP 模型

QP 模型卫星钟差预报表达式为

式中：x为预测钟差；i=(1，2，3，···，n)；a0、a1、a2分别为参考时刻卫星的相位、频偏和频漂；t0为卫星钟差的参考时刻；ε为残差.

1.2.2 SA 模型

SA 模型又称作附加周期项的QP 模型，是指在QP 模型的基础上考虑周期项的钟差预报模型，其数学表达式为

式中：a0、a1、a2与ε所代表的含义与式(2)中相同；n为主要周期函数的个数；Ak、fk、φk分别为对应周期项中的振幅、频率和相位.

与QP 相同，多个钟差序列经过最小二乘法求得参数的最或然值，并将其反带入式(3)即可进行钟差预报.SA 模型考虑了周期性变化对预报模型的影响，提高了其短期预报精度，模型结构相对复杂.但是模型主体仍是QP，也相应继承其模型随预报时长的增加其预报结果的准确度整体呈下滑趋势的缺点.

1.2.3 GM 模型

GM 模型的钟差预报表达式为

式中：k=(1，2，···，n)；a和u分别为发展系数和灰色作用量，是一个常数参数.多个钟差序列经过最小二乘法求得参数的最或然值，并将其反带入式(4)即可进行钟差预报.GM 模型因指数参数影响，参与的拟合历元数量严重影响预测精度，预测结果差异过大，易陷入局部最优的困局中.

2 PSO-Elman 模型基本原理

2.1 Elman 神经网络

神经网络在处理分析非线性时间序列的拟合和预测的问题上具有显性优势[16].Elman 神经网络的网络结构是将BP 神经网络的隐藏层转接到输出层的过程中加置一个承接层，接收并记录此刻迭代过程中隐藏层的输出结果.在某一次迭代过程中，参考系数选用上一次隐藏层的反馈信息，并将上一次的隐藏层输出值与此次输入层值按权属进入此次隐藏层中，当输出值与期望值间差值大于设定目标时通过上述过程反向调整网络进而逼近期望输出值，使网络训练具有局部的反馈性和动态短期记忆特征[17].这样的网络架构使得Elman 神经网络具备良好的时序特征和短期记忆能力，在钟差预报这种时间序列分析问题上有优秀的适配性.

Elman 神经网络通过输入层神经元传入信号，同时采用线性加权的方式经过隐藏层与承接层的计算得出结果后传输到输出层的神经元.其表达式为：

式中：z为隐藏层的输出值；k为输入层函数序列的标数；f为隐藏层传输函数；x为输入值；w1为输入层与隐含层间的权值；w2为隐含层与承接层的权值；w3为隐含层至输出层的权值；zc为承接层输出值；yk为输出层输出值；g为隐含层至输出层的传输函数.

激活函数使用sigmoid 函数，其表达式为

2.2 PSO 算法

PSO 算法通过模拟鱼群和鸟类觅食行为，是一种群体协作随机搜索优化、寻找单目标问题的最优解的智能算法[18-19].PSO 算法中，各个粒子都是搜索空间中没有体积与质量概念的独立解，并且有自己的位置和速度.根据搜索空间中粒子的位置和速度，随机初始化种群粒子，使用适应函数将每个粒子连续聚合到其自身的历史最佳位置.全局粒子群进化公式如下：

式中：d为参数尺寸，d=1,2,···，n；c为加速系数；和分别为第i个粒子的位置和速度；pbetsi为第i粒子适应值；gbest为全局适应值；w为权值；r为[0，1]区间内随机数.

对于局部PSO 算法，每个粒子根据其和相邻粒子的历史最佳位置pbest 调整其速度.局部粒子群的速度更新公式为

PSO 算法具备种群初始化随机的特点，解空间中的粒子都具有自己的属性(位置、速度)和适应值.粒子之间具备记忆、追随的特性，在解空间内随当前最优解搜索更新，并将适应值信息单向提供给其他粒子，使得所有的粒子能够快速地收敛于最优解.

2.3 PSO 算法优化Elman 神经网络的钟差建模

Elman 神经网络是通过反复训练模型来调节网络运算中各矩阵的权值和阈值，网络连接权重将误差平方和作为指标，反向传播反馈修正，使得输出结果愈发趋近于真实值.但是初始参数设置时涉及权值和阈值的选取会严重影响网络运算的收敛和精度，严重时会使网络的输出结果陷入局部最优，失去训练的意义[20].针对于Elman 神经网络的初始参数设置导致算法输出结果异常的情况，本文提出采用PSO 算法得到的初始参数赋予给神经网络，从而减小上述情况对算法结果的影响，大大提高了钟差预报的精准度.

通常网络中输出层的神经元个数与输出结果的类型相同.在滑动窗口模式下的单次钟差预报的计算最后输出的结果为某一时刻的钟差值，设置输出层个数为1.在样本总量不变的前提下，上一次计算出的钟差值也会参与到下一次的预报中，从而达到连续的多历元卫星钟差预报.

神经网络中的隐藏层神经元的个数对后续结果精度的影响至关重要.隐藏层神经元个数较多，网络的整体结构会更加稳定，但网络训练的收敛速度将大大增加，时间复杂度过高.隐藏层神经元个数较少，则网络结构简单，计算速度较快，但模型的预报精度降低[21].在保证模型预报精度的前提下，选择更加合适神经网络的架构将有利于后续工作的进行.为获取最佳的网络结构，本文选择2021 年9 月21 日WHU分析中心的精密钟差产品进行模拟实验，选自于C46号卫星分别在不同的神经元个数时进行12 h 的钟差预报.图1 为1～12 个神经元个数各自的均方根误差(RMSE)值变化情况.

图1 隐藏层不同个数神经元时的钟差预报RMSE

由图1 可知，隐藏层神经元数为3 时钟差预报精度最高，结构最为稳定.故本文采用的隐藏层神经元个数为3.

利用PSO 算法和Elman 神经网络结合进行钟差预报建模，得到PSO-Elman 模型具体步骤为：

1)将精密钟差产品预处理，对其中的异常值进行修正.将参与建模的钟差数据进行一次差分后设置为样品集，并将其进行归一化处理.

2)根据已规划好的的网络拓扑结构，定义算法中的迭代次数、加速系数、种群规模、速度与位移的最大和最小值、适应函数.本文中选取的适应函数为训练样本的预测值与真实值的均方根误差(RMSE)，表达式为

式中：m为样本个数；为真实值；yi为预测值.

3)初始化.在搜索空间内的个体粒子，其本身属性(速度、位置)都是随机产生的.粒子所在的当前位置即是自身的个体极值(即个体极值点的适应度值).当前具有所有个体极值最优解的粒子序号设置为全局极值，并将全局极值点设置为该粒子的当前位置.

4)评估个体粒子适应值.计算各粒子的适应度值，若某个粒子当前适应值比之前记录的该粒子最优值更好，则更新pbest.若某个粒子当前适应值比之前记录的全局最优解更佳，则更新gbest.

5)粒子群的更新.针对每一个粒子重复步骤3的速度与位置的更新.

6)检验是否符合输出标准.如果当前迭代次数达到设定的最大值或结果在标准范围误差内时，停止迭代，输出最优解.否则重复步骤4 和步骤5 过程直至满足条件位置.

7)将步骤6 算法中计算得出的结果赋予给神经网络权值和阈值的初始参数并开始训练，对钟差数据进行反归一化运算，验证样本中的预报值与真实值间的拟合差.

8)通过上述步骤训练完成的网络进行预报得出钟差序列结果，并逐步相加将其还原即可求得钟差预测结果.

3 预报实验分析

为了验证本文提出的PSO-Elman 模型的可行性，采用WHU 分析中心提供的30 s采样间隔的精密钟差数据进行模拟实验分析.针对不同预报时长，分别使用4 种模型进行1 h、3 h、6 h、12 h 的钟差预报实验.本次实验采用2021 年9 月21 日的钟差数据为例分析.在预报实验中使用RMSE 和极差(Range)作为评判标准，计算公式为：

式中：ti为预报值；为WHU 精密钟差数据；n为数据个数.

3.1 实验1

为了对比PSO-Elman 模型与Elman 钟差预报模型的预报性能，以C46 号卫星为例.两种模型采用已确定好的相同网络结构，以此次该卫星前12 h 作为样本数据进行建模预报后12 h 的卫星钟差，分别进行10 次独立预报实验.两种模型预测结果的RMSE值如图2 所示.

图2 10 次独立实验中两种模型预测的RMSE

由图2 可知，Elman 神经网络模型与PSO-Elman模型在针对一组数据进行多次实验后，所得结果无明显波动，证明了神经网络在钟差预报实验中的稳定性.10 次实验两组模型RMSE 的平均值分别为0.94ns和0.22 ns，表明经过PSO 算法优化Elman 神经网络后，克服了Elman 神经网络模型的局限性，预测精度提高了76.6%.

3.2 实验2

为了进一步验证PSO-Elman 模型不同预测时长时的预报性能，与三种传统钟差预报模型进行对比分析.图3 为C46 号卫星预报误差曲线.由图3 可知：PSO-Elman 模型预报效果在0 值左右；QP 模型与SA 模型预报效果相仿，并且这三个模型在0～200 历元内预报性能相当，但在其之后预报误差随着预报时长的增加整体呈递增趋势；GM 模型从0 时就具备一定量的偏差值，并且之后呈现显著递增.从整体趋势上不难看出PSO-Elman 模型预测精度更高，随预报时长增加所受影响相较于其他模型变化幅度更小.

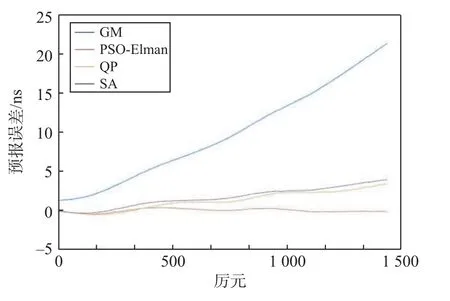
图3 C46 号卫星12 h 预报误差曲线

由表1 可知：在1h 预报时长的实验中PSO-Elman模型相对于QP、SA、GM 模型的预报精度分别提高90.0%、22.5%、99.7%，稳定度比QP、GM 模型提高了84.1%、95.8%，低于SA 模型58.1%，但处于一个量级；在3 h 预报时长的实验中其预报精度分别提高74.3%、47.20%、99.2%，稳定度分别提高81.9%、2.7%、97.8%；在6 h 预报时长的实验中其预报精度分别提高17.5%、56.0%、98.3%，稳定度比QP、GM 模型分别提高28.3%、95.6%，低于SA 模型9.4%，但处于同一量级；在12 h 预报时长的实验中其预报精度分别提高87.1%、89.3%、97.8%，稳定度分别提高77.5%、79.2%、95.6%.其中，在1 h 实验中SA 模型预测的初始值存在负方向偏差，极值偏小.钟差数据具有周期性变化，在6 h 预报时曲线变化与PSO-Elman 模型相仿，但随着预测时长增加整体发散，极值变大.在C46 号卫星的钟差预报中4 个不同预报时长的实验结果来看，PSO-Elman 模型RMSE 值对比于其他模型预报结果更加精准；Range 值表示整体误差范围内的最大绝对值，其数值越低则表明真值与预测值间的误差浮动区间越小且更为稳定.

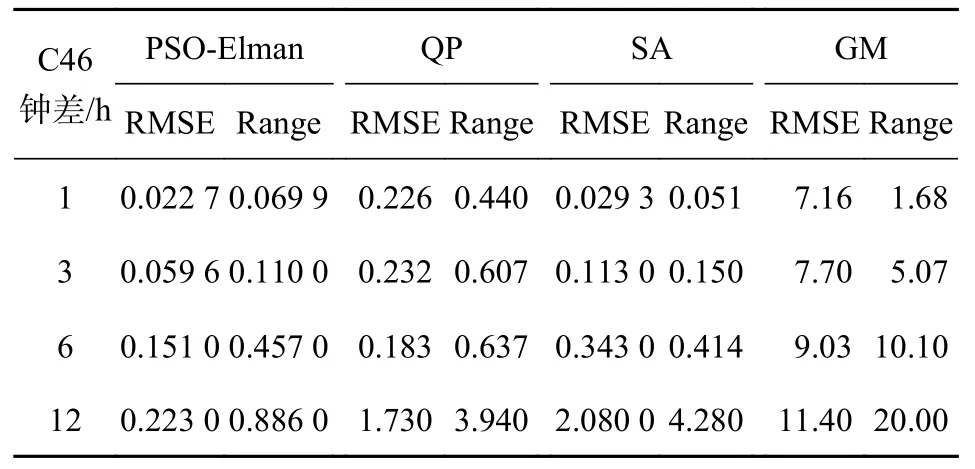
表1 C46 号卫星钟差预报结果统计 ns

3.3 实验3

对PSO-Elman 模型在不同原子钟类型情况下的预报性能进行分析对比.图4 为C19 号卫星12 h 预报误差曲线.在C19 卫星预报时，四种模型预报误差具备相似但不相同的变化趋势：PSO-Elman 模型与GM 模型在整体1 440 历元期间变化曲线大致吻合，但随着预测时长的递增GM 模型的精度变化略低于PSO-Elman；SA 模型变化趋势对比之前两者稍有逊色，在50 历元后呈负向递增；QP 模型在0～50 历元时尚与其余模型相当，但之后随着预测时长的增加整体呈现显著的负向递增.

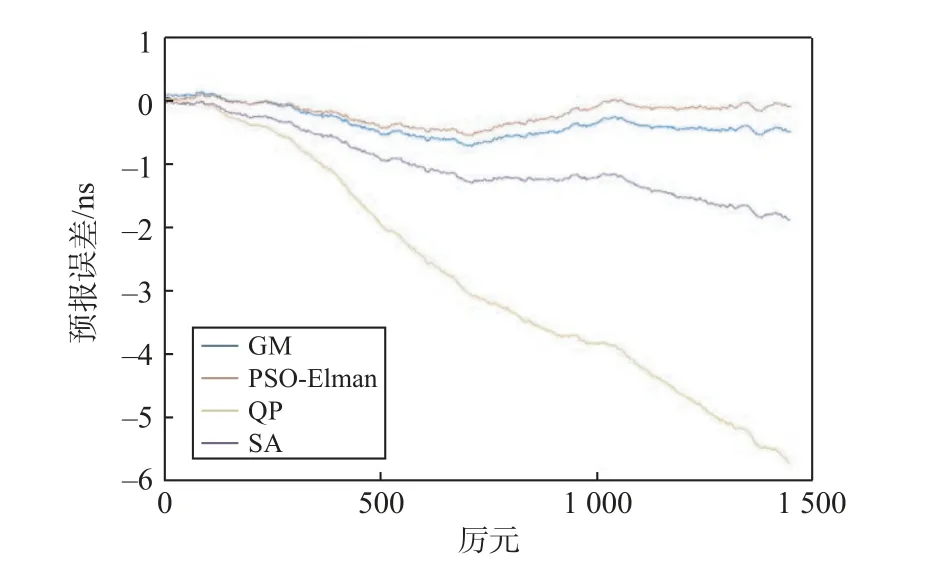
图4 C19 号卫星12 h 预报误差曲线

图5 为C38 号卫星误差曲线.在C38 卫星预报时，四种模型呈现不同的变化趋势：GM 模型在初始预报时存在偏差值，不过整个预报过程中浮动区间极小；SA 模型在整个预报过程中随着预报时长的增加呈递增趋势；QP 模型时与PSO-Elman 模型在初始时刻预测误差极其趋近于0 值，但随着预测时长的增加与SA 模型类似且呈负向递增；PSO-Elman 模型基本在0 值范围内浮动，变化极小，表明该模型在此次预报实验中预测值与真值误差精度更高.

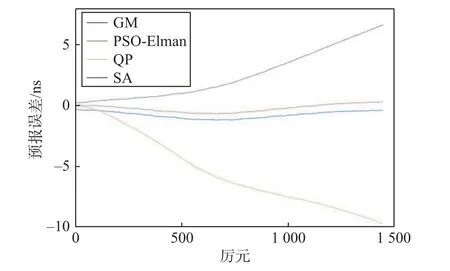
图5 C38 号卫星12 h 预报误差曲线

C19 号卫星为BDS-2 卫星，搭载的星载原子种类型为铷钟；C38 号卫星为BDS-3 卫星，搭载的星载原子种类型为氢钟；C46 号卫星为BDS-3 卫星，搭载的星载原子种类型为新型铷钟.

结合C19 与C46 号卫星情况分析，不同代的铷钟产品各个模型的预报性能情况不同：GM 模型BDS-2 铷钟的预测结果显然比在BDS-3 卫星新型铷钟效果更好；QP 模型在BDS-3 卫星效果更胜于BDS-2；SA 模型在新型BDS-3 铷钟上预测效果与QP 模型相仿，但在BDS-2 铷钟预测性能上比QP 模型效果更好，逊色于其他两者模型.

结合C38 与C46 号卫星情况分析，在BDS-3 卫星中，不同星载原子钟各个预报模型效果亦有差异：GM 模型在星载原子钟为氢钟时虽然初始值略有偏差，但是整体预测结果及稳定性上相较于铷钟预测性能更佳；QP 模型和SA 模型在不同原子钟上性能效果相仿，在星载原子钟为氢钟时随着预测时长增加呈现正负向递增，在铷钟情况下虽然也呈递增趋势，但波动幅度较比前者更为稳定且差异值更小，效果更佳.

POS-Elman 模型在BDS-3 的不同原子钟上所表现的情况相同，浮动区间基本在0 值内且随着预测时长增加所受影响极小；在BDS-2 铷钟情况时，区间浮动范围比其他情况下更为明显，但误差值亦在0 值左右波动.

由表2 可知，在C19 号卫星的短期钟差预报中PSO-Elman 模型对比QP、SA、GM 模型，在12 h 预报过程中其预报精度分别提高91.5%、75.9%、93.8%，稳定度分别提高88.5%、64.9%、22.7%.C38 号卫星的短期钟差预报中12 h 预报过程中其预报精度分别提高93.6%、87.5%、53.1%，稳定度分别提高90.0%、84.8%，但相较于GM 模型稳定度稍逊色10%.综合3 颗卫星对比于三种常用模型的优化精度平均提高90.7%、84.2%、81.6%，稳定度平均提高85.3%、76.3%、36.1%.从上述结果来看，PSO-Elman 模型在不同星载原子类型的情况下精确度更高、稳定性更强、预测误差波动间更小，所表现的预报性能更优.

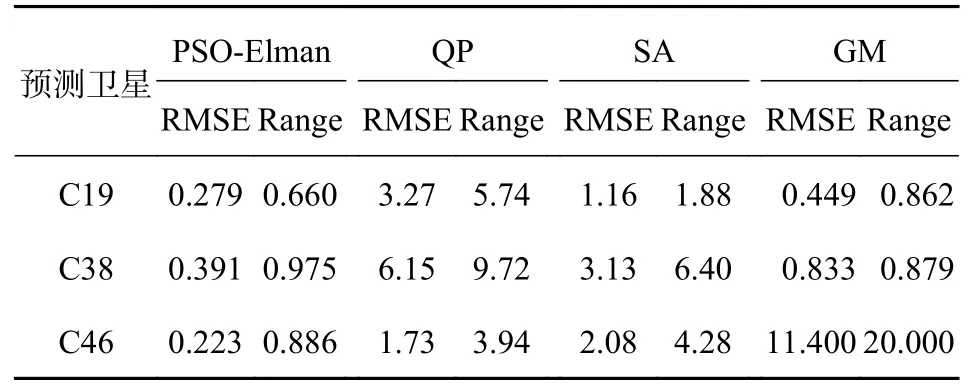
表2 3 颗卫星四种模型钟差预报结果统计 ns

4 结论

本文提出的采用PSO 算法优化Elman 神经网络的PSO-Elman 模型具有较强的自适应性，通过预报实验得出：

1)PSO 算法对Elman 神经网络的优化效果明显且精度提高了76.6%，且经过多次实验其结果差异不大，避免了偶然性.

2)经过4 次不同预测时长的模拟实验，在1～6 h除了灰色模型外都能达到亚纳秒级，在1～12 h 其余模型能达到纳秒级，而PSO-Elman 模型依旧能达到亚纳秒级.随着预测时长的增加传统模型拟合误差越来越大，PSO-Elman 模型受到预测时长增加影响极小，且预测精度具有显著优势.

3)根据星载原子钟种类不同的卫星预报实验，QP 模型与SA 模型更适用于BDS-2 的铷钟卫星；GM模型适用于BDS-3 的新型铷钟和氢钟；POS-Elman模型在这三种情况下皆适用且预测结果精度更高.

综上所述，相较于常用的三种传统算法模型，PSO-Elman 模型在不同情况下的钟差预报均能保证稳定度的同时，精确度更有显著提高，适用性更广泛，表明了此方法在短期钟差预报的可行性.