玩转图形还原 发展空间观念 感悟创新意识

苏柳燕

［摘 要］特级教师顾志能在“图形的运动”练习课中，以一张笑脸拼图帮助学生复习图形的运动方式，让学生在平移、旋转中玩转图形，经历三次思维头脑风暴。通过观摩并研讨该练习课的教学片段，创新教学方式，以发展学生的空间观念和创新意识。

［关键词］平移；旋转；空间观念

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）08-0062-03

人教版教材关于“图形的运动”的具体编排分为三个层次：“图形的运动（一）”（二年级下册），初步感知生活中的对称、平移和旋转现象，初步认识轴对称图形；“图形的运动（二）”（四年级下册），进一步探索图形构成轴对称的特征，能在方格纸上将一个轴对称图形补充完整，会在方格纸上画出平移后的图形；“图形的运动（三）”（五年级下册），进一步认识图形的旋转，能在方格纸上画出旋转90°后的图形，能从对称、平移和旋转的角度欣赏生活中的图案，并以单个或多个角度在方格纸上设计图案，增强空间观念。

《义务教育数学课程标准（2022年版）》（以下简称“课标”）指出：“空间观念主要是指对空间物体或图形的形状、大小及位置关系的认识。”图形的旋转属于“图形的位置与运动”中的内容。笔者观摩特级教师顾志能给六年级学生带来的“图形的运动”练习课，发现其通过追问，使学生同时复习平移、旋转的两种图形运动方式，由此获得了很大的启发。

一、课堂实录与赏析

1.引出新课，复习运动方式

师：关于图形的运动方式，同学们学过哪些？

生1：平移、旋转和翻转。

（1）复习平移

師（出示图1）：1号和2号要还原到原来的位置，该通过图形的哪一种运动方式还原？先说1号。

生2：用平移，1号向右平移2格即可。

师：看来说平移的时候有要求——方向和距离，向右是方向，2格是距离。

（2）复习旋转

师：2号怎么还原？

生3：2号先顺时针旋转 90°，再向下平移1格。

生4：我们还要说绕着哪个点旋转，应该是2号先绕着其所在正方形的中心顺时针旋转90°，再向下平移1格。

生5：2号也可以先向下平移1格，再绕其所在正方形的中心顺时针旋转 90°。

（教师让学生演示旋转）

师：同学们，描述旋转有哪几个要素？

生6：旋转中心、旋转方向和旋转角度。

（3）复习翻转

师：除了平移和旋转，图形的运动方式还有翻转，如1号要还原到原来的位置，可以怎么翻转？

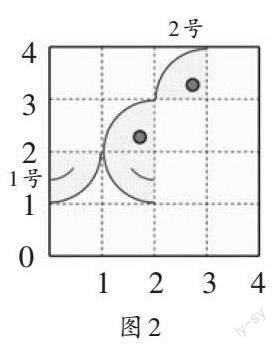
生7：将方格用数对表示（如图2），1号先以点（1，2）为中心向右翻转，再以点（2，2）为中心向右翻转。

师：1号翻转的时候是按点运动的吗？

生8（边说边演示）：不是，应该是沿第1列这条线向右翻转，再沿第2列这条线向右翻转。

师：以这条线进行翻转，这条线叫什么？

生（齐）：这条线叫对称轴。

【赏析】课标中提供了图画还原的教学案例，顾志能老师巧妙地利用课标中的学习素材，改变笑脸拼图中的1号和2号图片，引导学生从图形运动的角度把这2张图片还原，不仅复习了平移、旋转和翻转等图形的运动方式，还沟通了三种图形运动方式之间的联系和区别。同时，顾志能老师还引导学生用不同的图形运动方式还原1号图片，帮助学生体会图形还原方式的多样性，增强了问题的趣味性，打开了学生的思考空间。

2.挑战极限，思维头脑风暴

（1）找到图形的还原方法

师（出示图3，笑脸拼图背面图案和正面一样）：3号怎样才能实现还原？先仔细观察，再动手操作，找到还原方法。

生1：先以第3列这条线为对称轴向左翻转，然后向左平移1格，再向下平移1格。

生2：先向左平移1格，再以第2列这条线为对称轴向左翻转，然后向下平移1格。

师：大家的方法非常多，老师也有一种方法，先向左平移1格，再绕点（2，3）逆时针旋转 90°，最后向下平移1格。

【赏析】在这个教学环节中，顾志能老师对上一个环节的图形还原进行了难度和方法的升级，引导学生综合运用图形的三种运动方式描述3号图片的还原轨迹，达到四种训练目的：第一种是学生独立思考图形的还原方法，第二种是听懂其他学生边说边演示图形还原的过程，第三种是学生通过语言能想象其他图形还原的过程，第四种是学生通过观看演示用语言描述图形还原的过程。这种让学生经历想象、猜测和推理的训练，有助于学生理解图形的三种运动方式，培养其空间想象力和推理能力。

（2）用2步还原图形

师：我们将平移1格、旋转1次或翻转1次计1步，刚才老师的这种方法一共有几步？

生3：3步。

师（出示图3）：刚才大部分同学都用了3步，若用2步，怎么还原3号图片？

生4：先绕点（3，3）顺时针旋转180°，再绕点（2，3）逆时针旋转270°。

师：成功了吗？下面有同学给你提了小建议，逆时针旋转270°，也可以是顺时针旋转90°。谁来分析一下这位同学用2步能够实现还原的奥秘？

生5：我发现重点是第一步，他的第一步相当于一次走了2步，再走1步就能还原了，所以他只用2步就能还原。

师：还有其他方法吗？

生6：先绕点（3，4）顺时针旋转90°，再绕点（2，3）逆时针旋转180°。

师：这位同学是用旋转来实现2步还原，还有其他方法吗？

生7（边演示边说）：先绕点（3，3）逆时针旋转90°，再以点（1，4）和点（4，1）的连线为对称轴翻转1次。

师：你的奥秘在于一条很特别的对称轴。相信你还有不同的方法，请你再说出一种方法，不要直接演示，让其他同学想一想。

生7：先以点（2，4）和点（4，2）的连线为对称轴翻转1次，再绕点（2，3）顺时针旋转90°。

师：咱们来演示一下，成功了吗？还有不一样的对称轴、不一样的方法吗？

生8：还有很多条对称轴。一种方法是以第2列和第3列这两条线中间的一条竖线为对称轴翻转，再向下平移1格。另一种方法是以点（1，4）和点（4，1）的连线为对称轴翻转，再绕点（2，2）顺时针旋转 90 °。

……

【赏析】在这个环节中，顾志能老师遵循学生的认知规律，设计任务从简单到复杂，让学生有信心去挑战下一关。在学生有了一定的经验后，再借助学具，“逼”着学生用2步还原图片，同时用掌声和语言不断地鼓励学生勇于挑战自我。学生在一次次的尝试中发现变换旋转角度、找旋转中心和特别的对称轴等方法都可以使3号图片距离原来的位置越来越近。同时，学生在他人的发言中不断获得启发，萌发新的想法，促使数学思维更加深入。

（3）只用1步还原图形

师：同学们，刚才我们用2步来还原，能用1步来还原3号图片吗？用刚才这些方法动手试一试，你的窍门是什么？是对称轴，还是旋转中心？

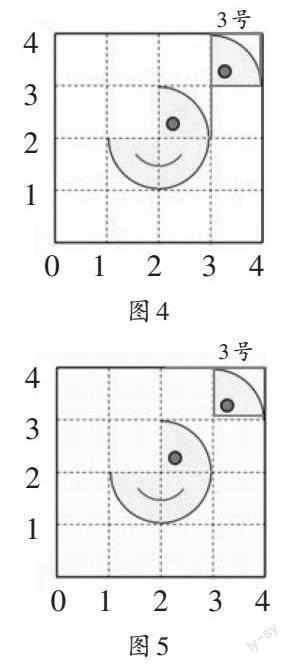
生9：先将点（3，2）、点（3，4）的连线和3号图片看作一个整体（像一面小旗，如图4），再以点（3，2）为旋转中心，将“小旗”逆时针旋转 90°。

师：这样的旋转方式不仅有创意，还给我们带来了启发。你想到其他方法了吗？

生10：将点（2，4）、点（4，4）的连线作为“小旗”的旗杆（如图5），以点（2，4）为旋转中心，顺时针旋转90°。

师：顺时针旋转？不行哦！但是你的奇思妙想值得点赞。

【赏析】在这个环节中，顾志能老师继续带领学生脑洞大开——只用1步还原图形。学生凭借上一个环节获得的变换旋转角度、找旋转点和对称轴等方法和经验，在想象和试错中探究出只用1步还原图形的方法，真正发展了空间观念。同时，顾志能老师还肯定了主动思考的学生，虽然学生的结论错了，但是奇思妙想和创新意识值得鼓励。这种做法保护了学生的学习积极性。

3.全课小结，畅谈学习收获

师：同学们，通过今天这节课，你有什么收获？

生1：我们知道了图形的运动方式有平移、旋转和翻转，平移要说清楚方向和距离，旋转要说清楚旋转中心、旋转方向和旋转角度，翻转要说清楚对称轴。

生2：这节课我们玩了笑脸拼图，知道了同一个问题可以从不同的角度来思考。

生3：我们在数学学习中要有创新思维。

二、对空间观念和创新意识教学的启示

顾志能老师的“图形的运动” 练习课精彩地诠释了要如何培养学生的空间观念和创新意识，值得广大教师学习和借鉴。

1.培养空间观念，要多做、多想、多说

教师要想在数學课堂中渗透空间观念，就要努力做到让学生多做、多想、多说。顾志能老师在这节课中围绕笑脸拼图设计了五次动手和动脑活动：还原1号图片、还原2号图片、用各种方法还原3号图片、2步还原3号图片、只用1步还原3号图片。同时，顾志能老师还采用多种方式发展学生的空间想象力，如让学生先想再拼、将别人拼的与自己拼的做比较、听语音摆、用语言描述图片的移动轨迹等。学生只有充分经历动手和动脑的活动过程，才会从不同角度想象图形运动前后的位置关系，才能在头脑中对图形进行变换与比较。

2.培养创新意识，要鼓励敢做、敢想

创新意识作为小学数学核心素养之一，具体表现是：（1）对数学及数学学习有好奇心；（2）乐于在数学探究中提出猜想与问题；（3）愿意尝试不同的方法与策略；（4）能够独立思考，具有质疑问难的批判精神；（5）感悟和欣赏数学的神奇与美。顾志能老师在培养学生的创新意识中，遵循了两个关键原则：第一是鼓励原则，学生的数学能力水平各不相同，但他都不断地鼓励学生去尝试和发现；第二是“爬梯子”原则，他设计了阶梯式的学习任务，帮助不同数学能力的学生得到不同的发展。

总之，数学课不是素材越多，教学效果就越好，简单的素材也能上好数学课，关键在于教师如何利用简单的素材帮助学生开展有效的学习活动。同时，数学课不仅要落实显性的数学知识和数学技能，还要渗透隐性的数学活动经验和数学思想方法，如此才能让学生会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。

［ 参 考 文 献 ］

[1] 杨兴谱，顾志能.知识整体建构  素养有效提升：六年级“图形的运动（练习）”教学实践与思考[J].教学月刊小学版（数学），2022（11）：23-27.

[2] 孔忠伟.修身养言，融合教学：提高数学语言表达水平：听特级教师顾志能《图形的运动练习》有感[J].小学教学设计，2022（11）：63-65.

[3] 郭建平，顾志能.观察、操作、想象：让空间观念发展清晰可见：“‘图形的运动练习课”教学实践与评析[J].教学月刊小学版（数学），2020（3）：18-21.

（责编 覃小慧）