游戏“设计”背后的奥秘

文／喻洋

同学们设计过游戏规则吗？事实上，游戏规则的制定蕴含了丰富的数学知识，尤其与概率有很大的关联。概率思维其实是一种数学思维，它能帮助你从不确定中找到确定性，是一种十分有效的决策工具。下面，我们结合2022年的几道中考试题，带领同学们一探究竟。

一、利用概率设计抽奖规则

例1 （2022·江苏扬州）某超市为回馈广大消费者，在开业周年之际举行摸球抽奖活动。摸球规则如下：在一只不透明的口袋中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后先从中任意摸出1 个球（不放回），再从余下的2个球中任意摸出1个球。活动设置了一等奖和二等奖两个奖次。现规定摸出颜色不同的两球和摸出颜色相同的两球分别对应不同奖次，请写出它们分别对应的奖次，并说明理由。

【分析】从商家的立场进行考虑，一等奖的奖品更加昂贵，为了体现其稀缺性，一等奖的获奖率应该低于二等奖。该游戏规则需要摸球两次，可以用树状图法不重复、不遗漏地列出所有可能的结果，最终选择概率更低的摸球方案为一等奖。

解：画树状图如下。

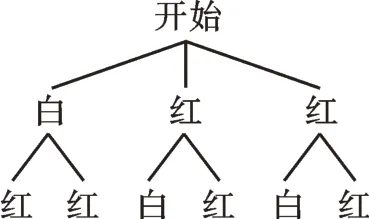
二、利用概率设计游戏镖盘

例2 （2022·江苏徐州）将一枚飞镖任意投掷到如图1 所示的正六边形镖盘上，若飞镖落在镖盘上各点的机会相等，则飞镖落在阴影区域的概率为（）。

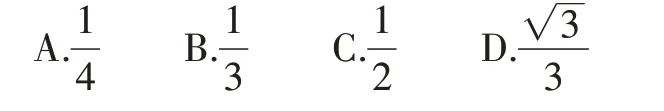
图1

【分析】飞镖是一款具有挑战性的游戏，设计者将镖盘划分为阴影和非阴影两部分。我们根据几何概率可以预估将一枚飞镖任意投掷于阴影部分的概率，即阴影区域的面积与总面积的比值。

解：如图2，我们可以将整个图形分割成图2 中的小三角形。设每个小三角形的面积为a，则阴影的面积为6a，正六边形的面积为18a，所以将一枚飞镖任意投掷到镖盘上，飞镖落在阴影区域的概率为。故选B。

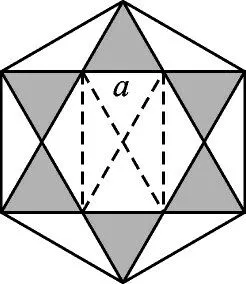
图2

三、利用概率设计摸球方案

例3 （2022·山东青岛）学校想请一位同学作为代表分享获奖心得。小冰和小雪都想分享，于是两人决定一起做游戏，谁获胜谁分享。游戏规则如下：

甲口袋装有编号为1、2 的两个球，乙口袋装有编号为1、2、3、4、5 的五个球，两口袋中的球除编号外都相同。小冰先从甲口袋中随机摸出一个球，小雪再从乙口袋中随机摸出一个球，若两球编号之和为奇数，则小冰获胜；若两球编号之和为偶数，则小雪获胜。

请用列表或画树状图的方法，说明这个游戏对双方是否公平。

【分析】设计双人游戏，关键是确保规则的公平性。评估游戏是否公平可以通过列表或画树状图的方法求出规则中双方赢得游戏的概率，然后再比较这些概率的大小。若概率相等，则游戏公平；若概率不相等，则该游戏不公平。

解：我们可以先用列表法将所有可能发生的结果列出来，所有可能的结果如下：

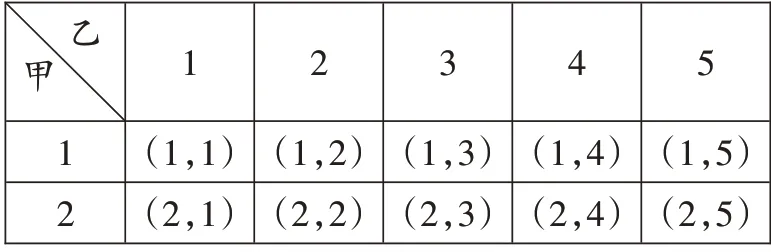
甲乙_____________________________________1_____________________________________2 1 2 3 4 5（1，5）（2，5）（1，1）（2，1）（1，2）（2，2）（1，3）（2，3）（1，4）_______（2，4）_______