排除统计问题中的定势效应之“雷”

文／帅建卓

信号一响，位于起跑线上的运动员便飞奔而去，这就是定势效应。定势效应有的时候有正面作用，如运动员听到发令枪响，就迅速起跑，哪怕是比对手早0.01 秒，也可能赢得比赛的胜利。但定势效应更多地会产生负面的影响。比如：同学们在研究统计问题时，常常有“一见如故”的感觉，请注意，此时你很可能遇到定势效应的“雷区”，形成错误的判断与决策。如何克服这种情况呢？请看下面的3个小妙招。

一、巧用直观，排多算之“雷”

例1 如图1是甲、乙五次测试成绩的折线统计图，则平均成绩更好的是____，成绩更加稳定的是。

图1

【点评】当需要比较两组数据的统计量时，我们习惯性想到的是计算。事实上，数据的离散程度不一定通过计算方差反映，有时可以从散点图中直观看出。我们从图中不难看出：甲5 次的成绩整体波动更小，因此更加稳定。另外，我们通过散点图对比也能发现，甲、乙5 次成绩中有三组分别相等，另外两组均为乙更高，因此乙的平均成绩更好。充分利用图表“直观”解决统计问题，是排多算之“雷”的好方法。

二、明晰概念，排误解之“雷”

例2 为了解学生的睡眠状况，学校调查了某班50 名学生每天的睡眠时间，绘成睡眠时间频数分布直方图，如图2 所示，则所调查学生睡眠时间的众数为________h，中位数为________h。

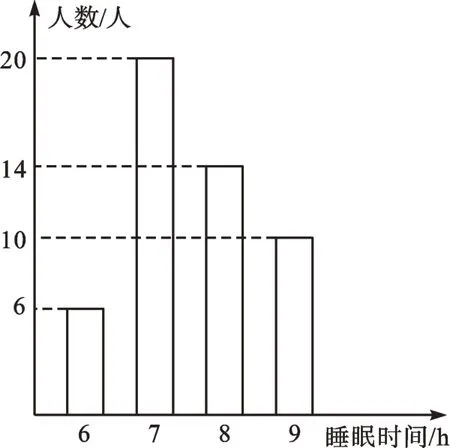
图2

【解析】因为睡眠时间7 小时的人数最多，所以众数为7h；把睡眠时间从小到大排列，第25、26 位学生均为7h，所以中位数为7h。

【点评】此题看似简单，却经常出现如下错误：众数为20 人，中位数为7.5h。究其原因，是有同学将数据与频数混淆。图2 中，横轴表示大致睡眠时间的四种类型，题中50 个数据均由6h、7h、8h、9h 组成。而纵轴表示人数（频数），反映四种睡眠数据出现的频数，因此这些数字并非50 个数据中的任何一个。由此看来，明晰数据与频数等概念的内涵，是排误解之“雷”的重要手段。

三、理性分析，排误判之“雷”

例3 农业、工业和服务业统称为“三产”，2021 年某市“三产”总值增长率在全省排名第一。观察下列两幅统计图，回答问题。

（1）2017—2021 年农业产值增长率的中位数是________%；若2019 年“三产”总值为5200 亿元，则2020 年服务业产值比2019 年约增加________亿元（结果保留整数）；

（2）小亮观察折线统计图后认为：这五年中，每年服务业产值都比工业产值高，你同意他的说法吗？请结合扇形统计图说明你的理由。

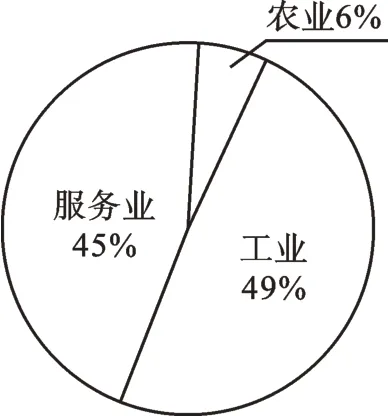
2019年某市“三产”产值分布图

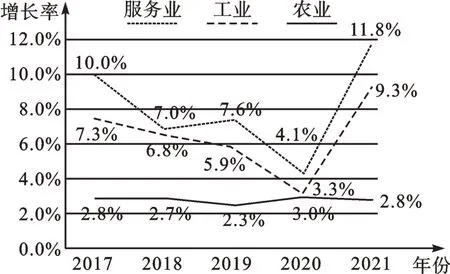
2017-2021年某市“三产”产值增长率折线统计图

【解析】（1）将2017—2021 年农业产值增长率按照从小到大排列，中位数为2.8%；2019 年服务业产值为5200×45%=2340（亿元），2020 年服务业产值比2019 年约增加2340×4.1%=95.94≈96（亿元）。

（2）不同意。虽然每年服务业产值的增长率都比工业产值的增长率高，但不知道每年的具体产值的基数和占当年的百分比，所以小亮的判断错误。

【点评】此题第（2）问很容易掉进定势效应的“雷区”。因为直观发现：越靠上的点取值越大，所以容易误认为小亮的判断正确。而问题中比较的是产值，还包含着服务业与工业的具体基数和占当年产值的百分比。解决本题的关键在于理解折线统计图反映的是增长率。唯有认真审题，理清数量之间的关系，才能主动规避定势效应带来的误区，排误判之“雷”。