动态的眼光·美学的体验

陈元云 邢成云

【摘要】数学中的很多知识、方法能实现科学与艺术的融合统一，数学追求美也创造美.本文以人教版《三角形的高、中线、角平分线》教学为例提出“用动态之眼光，享美学之体验”的课堂创新策略，引导教师将静态教材变为动态学材，帮助学生研究动点问题，形成一般观念，积累数学学习经验，提高核心素养，实现数学学科育人的根本任务.

【关键词】动静结合；触类旁通；核心素养

《义务教育数学课程标准（2022版）》（以下简称《2022版课标》）在课程性质部分指出“数学承载着思想和文化，是人类文明的重要组成部分”[1].伽利略稱数学为“书写宇宙的语言”，亚里士多德则认为“数学能促进人们对美的特性——数值、比例、秩序等的认识”.这些都道出了数学作为基础自然学科的美学价值.

三角形作为最简单的封闭几何图形，它具有“统领全局”的研究价值，因为它是后续学习其他封闭几何图形的直接基础，“文[2]”对其已经进行了诠释.本节课顺承文[2]，是教育部全国“双名”领航工程邢成云名师工作室提出的大单元主题教学“1＋n”（“1”指章起始课，即上面提到的文1）中n的第一节课，是立足起始对三角形的“三线”进行的“深度探研”课.三角形的边、角与三角形的“三线”共同构成了三角形的基本要素与相关要素，通过对三角形基本要素与相关要素的一般化、特殊化研究，便形成了几何图形的一般观念.本文拟从动态观念出发，由“一般——特殊”探讨并研究三角形的“三线”，其中数量关系与位置关系的一致性、对应性，数形结合、动静结合、特珠一般、具象与抽象等对立统一，无不体现出数学的内在魅力与辩证之美.

1背景分析

《2022年版课标》课程目标部分指出：“通过数学的眼光，能够抽象出数学的研究对象及其属性，形成概念、关系与结构[1]5”，这是当前数学教育背景下对学生核心素养提出的要求之一.这就呼吁一线教师要改变原来传统落后的教学理念与教学方式.而现实中以“育知”为主的教学理念，以“碎片化”为主的教学形式还没有得到很好的扭转.诸如对数学的一般观念、数学之美、动态观念等认识仍不足，很多教师忽视或漠视了这一点，面对可利用的教材资源，不能很好地挖掘，致使课程本身的价值难以实现；课堂教学仍停留在点对点的传授知识或就题讲题、以题练题的低浅层面，这些都应然是教师教学设计和践行课堂教学时需要规避和调适的.

2教材分析

文1（起始课）中，由线段的中点、角的平分线、三角形的面积这三个核心问题，初步形成了对三角形“三线”的认知.这种初步认知只是建立在原有知识基础上的一些肤浅认识，因此本节课是在顺承起始课（文1）的基础上，对三角形的“三线”从数学内部逻辑角度进行的分析与探究.同时，在理解“三线”的基础上，适时补充三角形的“内心、重心、垂心”的概念，帮助学生形成三角形较完整的认知体系，为后续学习引好方向，埋下种子，打牢基础，做好铺垫.

3教学设计

3.1创境引悱，孕育问题

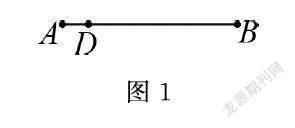
问题1：如图1，点D在线段AB上由点A→点B运动，此过程中，AD与BD的关系如何变化？

预设1：不管点D怎样运动，永远有AD＋BD＝AB.

预设2：点D在运动过程中，AD在变大，BD随之减小，若设AD－BD＝x，x的值由负数→0→正数.

追问：你感觉在这个变化过程中值得研究的是点D运动到什么位置时？

预设：点D为线段AB的中点时最特殊，此时x＝0，也就是AD－BD＝0.

追问：除以上最特殊的情况外，还有其它特殊情况吗？

预设：点D可以运动成为线段AB的三等分点或四等分点或……n等分点时，虽然x的值不特殊，但点D的位置都很特殊，会产生AD∶BD＝1∶2或1∶3或……1∶（n－1）等固定比.

追问：受前面问题启发，如图2，射线OD在∠AOB的内部旋转时，你能提出什么问题？

师生谈话，类比得出射线OD的特殊位置与相应的结论.

设计意图问题1旨在唤醒学生对线段中点、三等分点、n等分点的认识，用动点运动的形式激活思维，帮助学生认识n等分点的数学本质，从数学思维的角度学数学、用数学.最后的追问是对问题1的类比迁移，学生在思考过程中不仅加深了对知识的理解，更重要的是学会迁移与运用，渗透了策略性知识的学习.同时，通过几何量的大小比较发现0对应着几何图形的特殊状态，达成数量关系与位置关系的和谐统一，数形结合中透出数学的统一美.

3.2设疑猜想，形成模型

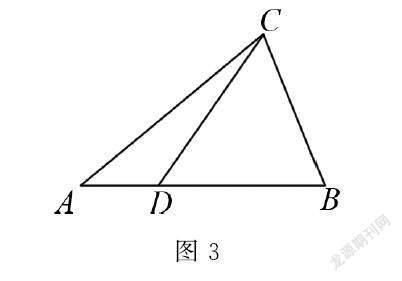
问题2：如图3所示，在△ABC中，点D是边AB上的一个动点，连接CD，△ABC中产生了哪些新的图形？点D在由点A→点B运动的过程中，这些新图形之间又会产生什么新关系？

预设1：产生了新的线段、新的角、新的三角形.比如：AD、BD，∠ADC、∠BDC，∠ACD、∠BCD，△ADC，△DBC.

预设2：点D在由点A→点B的运动过程中，AD与BD，∠ADC与∠BDC，∠ACD与∠BCD的差可能为负、可能为0、也可能为正，也就是它们之间的关系不确定.

追问：你认为这些关系中，哪种关系最特殊？

预设：当AD＝BD，∠ADC＝∠BDC，∠ACD＝∠BCD时是最特殊的.

师生谈话：当点D在AB上运动时，上面每两个量的差是变化的，这个变化过程是连续的，并且差的值分别由正值变为负值或者由负值变为正值.这其中包含了值为0的特殊情况.

设计意图问题2由问题1类比而来，学生发现其中的关系是自然的，借助点D的运动，让学生寻找三角形中产生的新图形，利用新图形之间的量差寻找运动过程中的特殊情况，从“数”的角度认识三角形的“三线”，同时为从“形”的角度认识三角形的“三线”做铺垫.这种体验是帮助学生经历动态的审美过程，加深对静态教材的理解，在这种具体的数学逻辑思考与数学探究活动的过程中，让学生对数学美有感受、有感悟，最终将数学美进行拓展并再创造.

3.3合作探究，得出模型

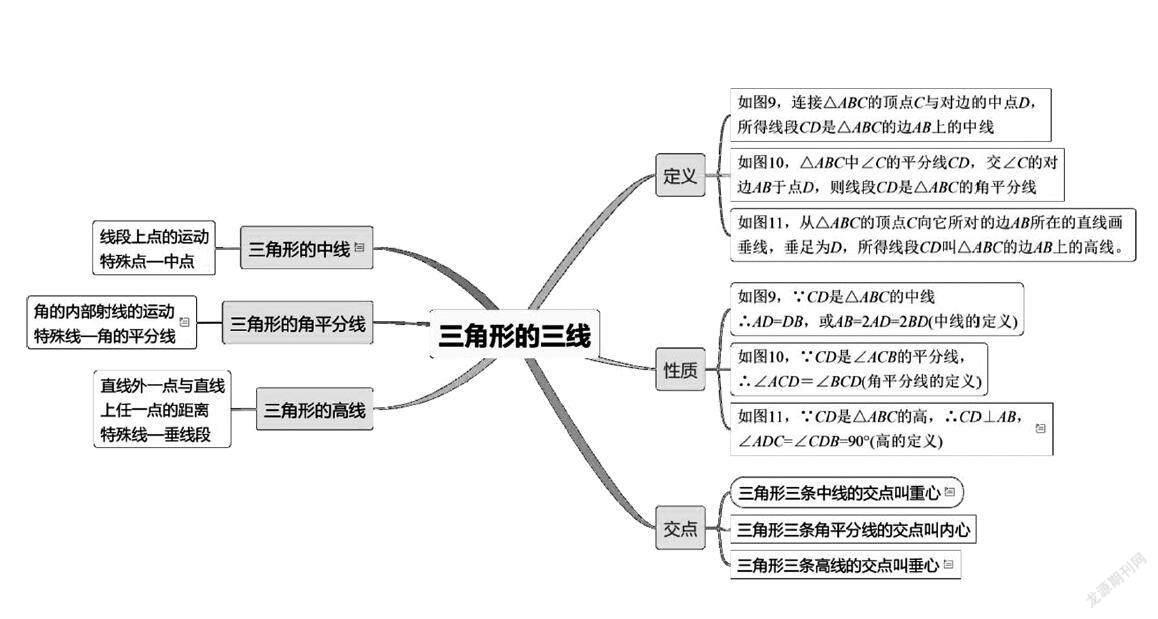
问题3：图4中，当AD＝BD，∠ADC＝∠BDC，∠ACD＝∠BCD时点D是最特殊的，每种情况下，特殊的线段CD分别称之为什么？

预设：当AD＝BD时，此时线段CD叫△ABC的边AB上的中线；当∠ADC＝∠BDC时，此时线段CD叫△ABC的边AB上的高线；当∠ACD＝∠BCD时，此时的线段CD叫△ABC的角平分线.

追问：当△ABC的形状发生改变时，上面点D的特殊情况都存在吗？

先请同学们独立思考，再小组合作，借画图进行验证，教师结合学生情况用几何画板动画演示.

预设：当△ABC的形状发生改变时，∠ADC与∠BDC的差为0这种情况可能不存在.其他的两种特殊情况都存在.

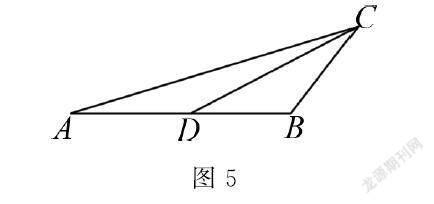
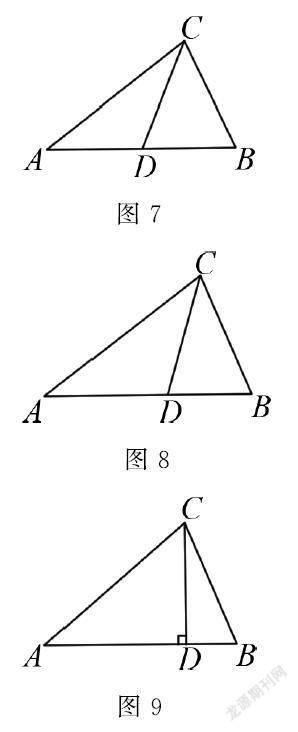
追问；如图5所示，当∠B＞90°（△ABC为钝角三角形）时，

此时∠ADC与∠BDC的差确定吗？

预设：∠ADC与∠BDC的差一定为正数，不可能为负数和0.

追问：此时，△ABC的边AB上的高线不存在了吗？

预设：应该存在，三角形的每条边都有高，不可能不存在.

追问：此时边AB上的高线如何做出？

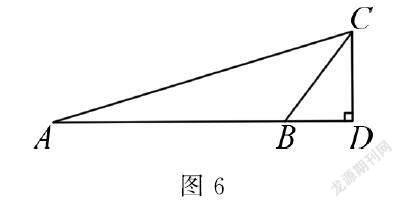
预设：当点D满足∠ADC与∠BDC的差为0时，此时的点D在线段AB的延长线上.如图6所示，过点C向AB的延长线做垂线（CD⊥AB）.

追问：△ABC的边AB上的高线在三角形的外部，钝角三角形的高都在三角形的外部吗？

教师根据学生回答配以几何画板动画演示.

设计意图准确画出钝角三角形的高线是本节课的难点，也是很多教师易忽略的，问题3借助开放变式，帮助学生在理解数学本质的同时，无形中也解决了难点.几何画板的动画演示，加深了学生对三角形高线的认知，自此，他们的感知也由感性上升到理性.

3.4再次探究，拓展模型

问题4：三角形的“三线”是动点运动中的特殊情况，大家想过这三条线又会出现什么特殊情况吗？

预设：三条线中的两条可能重合，比如角的平分线与中线可能重合，…….

追问：这三条线可能重合吗？也就是满足上面特殊情况的点D会不会成为同一个点？

学生此时会产生困惑，教师可借助几何画板的动画演示，让学生观察，不断改变三角形的形状，当三角形→等边三角形时，三角形的三线重合，也就是满足所有特殊情况的点D成为同一个点.

问题5：请大家分组画出不同形状（锐角三角形、直角三角形、钝角三角形）的三角形所有的“三线”（1-2组画不同形状三角形的中线，3-4组画不同形状三角形的角平分线，5-6组画不同形状三角形的高线），看看有没有新发现？

预设：不管三角形的形状如何，同一三角形的三条线一定相交于同一个点.

追问：“三线”虽然不同，但它们各自的三条线分别交于同一个点，这样形成了三个点，那这三个点的意义相同吗？我们可以借助什么区分这三个点？

预设：因为这三点是不同三线的交点，因此可以给它们不同的命名.

师生谈话：大家想法很好，三条中线的交点称之为重心，三条高线的交点称之为垂心，三条角平分线的交点称之为内心.

追问：这“三心”既然是特殊情况下产生的，大家猜想一下，这“三心”是否具备特有性质？你还能提出什么新的问题？

预设：对“三心”的性质学生可能会有阻力，但学生可能会提到，三线在特殊情况下会重合，那三角形的“三心”会不会重合？

设计意图此环节是对三角形“三线”的拓展与延伸，把“三线’推向对应的“三心”，提升对“三线”的认识，尤其是“三线”是否重合、“三心”的得出、“三心”的性质，这些均是顺承一步一步探索而获得的，是几何直观发挥作用的结果，不深入探究而点到为止，目的只是为后续学习埋下“种子”，帮助学生初步建构三角形这一基本图形的认知体系，便于加深他們对三角形的整体认识而已.

3.5反思评价，总结模型

问题5：请大家结合“三线”的学习过程，谈一下收获？

引导学生从“如何得出三线，如何对三线进行研究，如何拓展”三个方面进行总结.帮助学生完成本节课的知识结构图.

3.6解决问题，运用模型

结合教材习题11.1的第4题、第8题、第9题，对接本节课所学，试试能提出哪些问题？

设计意图聚焦三角形“三线”知识点，借助开放变式，在巩固新知的同时，加深学生对“四基”的理解.特别说明：若这一环节课堂完成不力或不能完成，可作为课后作业处理.

4教学立意的进一步阐释

4.1“动静”结合，触类旁通

因本节课是人教版八年级上册的内容，与学习线段、角的内容时间跨越了一个多学期，故在此通过两个问题唤醒学生对这一研究方法的认识.掌该该方法，对从运动变化的角度理解三角形的“三线”有很大的指导意义.同时，学生学会了这种思考问题的方法，形成了这样的一般观念，对后续学习四边形、圆等图形都会产生迁移力，此即为“触类旁通”的意义所在.

4.2以静制动，“鱼渔”共赢

从知识层面，本节课主要学习了三角形的“三线”；从方法层面，本节课主要引导学生从“运动变化”角度理解三线的概念，学会“动点运动”问题的解决方法，可以说，这种思考问题的方法在数学教学中比概念的获得更重要.为此，本节课提出“动静结合，触类旁通”的课堂教学策略，旨在帮助学生形成此类问题的一般观念：以静制动，动静互助，帮助学生积累数学的学习经验与思维方法.

4.3以美启真，文理相融.

本节课自始至终可以称之为一次感知、体验数学美的学习旅程.其一，统一之美（和谐美）.统一性反映的是审美对象在形式或内容上的某种共同性、关联性或一致性，数学对象的统一性通常表现为数学概念、规律、方法的统一.其二，整体之美.首先是本节课的整体定位，即用整体观念、整体教学法组织整节课的教学，从完善的角度进一步研究三角形的性质，除了三角形的边、角等本体元素外，还有紧密相关的其它元素——三线，尤其是线段中点与中线的关联、角的平分线与三角形角平分线的关联、垂直与三角形高线的关联等，这些都彰显出前后知识的结构性、联系性、发展性；其次，本节课不是着眼于研究“三线”各自的一条，而是穷尽所有去探索，从而出现了三角形著名的“三心”.其三，辨证之美.纵观整个设计，动与静、一般与特殊、数与形、具象与抽象、道法与术器等展露出的辩证之美，让数学教学有了哲学的味道.整个设计“润物无声”地体现了数学特有的“真、善、美”，知识、能力、素养融为一体，让数学教学有了高度.

【基金项目：山东省教育教学研究重点课题“基于初中数学课程整合的单元教学案例研究”（项目编号：2020JXZ026）的阶段性研究成果.】

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022版）［S］.北京：北京师范大学出版社，2022：1.

[2]邢成云.顺承已有知识，厘定研究路径[J].教育研究与评论（中学教育教学），2022（7）：53-58.