基于BP神经网络的手部尺寸预测模型构建

李炘 吴金颖 苏慧敏 潘怡婷 邹奉元

摘要： 针对手部尺寸测量项目多、繁杂的问题，文章提出构建基于数据驱动的数学模型来预测手部尺寸的方法。通过三维扫描仪采集232名在校女大学生手部三维点云数据，构建辅助点、线、面标准化测量方法，获取人33项特征部位尺寸，运用主成分分析得到影响手部形态的5个因子，采用相关指数最大值法获取手长、手宽、中指长、食指近位指关节围、无名指到腕中心距离5个典型指标，分别构建了BP神经网络、多元线性回归手部尺寸预测模型。结果表明：BP神经网络预测模型的MAE较低，相关性系数R2接近于1.000，25项手部尺寸的Sig.值大于0.050，预测效果良好，稳定性较高。研究结果可为通过少量易测量的手部尺寸预测其他手部尺寸提供参考。

关键词： 手部尺寸测量;相关指数最大值法;多元线性回归;BP神经网络;预测模型

中图分类号： TS941.17

文献标志码： A

文章编号： 1001-7003（2023）05-0059-07

引用页码： 051108

DOI： 10.3969/j.issn.1001-7003.2023.05.008

基金项目：

文化和旅游部重点实验室开放基金项目（2020WLB09）;国家级大学生创新创业训练计划项目（202210338032）

作者简介：

李炘（1995），女，硕士研究生，研究方向为服装数字化技术。通信作者：邹奉元，教授，zfy166@zstu.edu.cn。

在手部测量过程中，手的肌肉组织会发生不自主运动和软组织的变形，收集正确的手部特征部位尺寸的方法也可能具有挑战性［1］。由于手部需测量尺寸较多且精细，不易测量，因此有必要探索更便捷的手部尺寸测量方法。

关于手部测量研究，Garcia等［2］使用人体网格板测量法获取120名女性的33项手部特征部位尺寸，研究结果为手部工具设计提供了参考依据。Cakit等［3］使用电子数显卡尺等工具收集了土耳其92名男性和73名女性的20项手部特征部位尺寸，为土耳其本土牙医手部工具设计提供参考。但上述研究均为接触式测量法，测量前需对测试人员进行标准化测量培训，且准备工作及测量过程较为费时。由此，非接触式测量法被提出。Vergara等［4］先将被测试者手部放在校准网格纸上进行图像收集，成功实现手部尺寸测量。Fan等［5］提出一种基于图像的标记分水岭算法对手部特征部位进行测量，该方法降低了手部测量时间。但图片测量法在获取掌厚、手指围度等三维手部尺寸方面受限于手部拍照的角度与姿势。范丹镱等［6］提出线性回归数学模型法，首先通过Pearson相关性分析剔除了与手长、手宽相关性较低的手部特征部位，利用线性回归构建了手长、手宽与各指长、掌长等特征部位的回归模型。但获取手部尺寸还存在测量项目多且繁杂等问题，本文旨在通过相对容易测量的少量指标，构建基于数据驱动的预测模型，得到更多的手部尺寸。

本文提出基于数据驱动的数学模型进行手部尺寸预测。采用主成分分析及相关系数最大值法确定手部典型指标;分别构建了BP（Back Propagation）神经网络、多元线性回归预测模型对手部尺寸进行预测;以MAE（平均绝对误差）、R2（相关系数）、配对样本T检验Sig.值作为评价指标，分析两种模型的预测精度，为简化测量过程、获取手部尺寸提供参考。

1 实 验

1.1 测量对象

为保证样本代表性与独立性，根据GB/T 16160—2017《服装用人体测量的尺寸定义与方法》，实验随机抽样选取240名18～25周岁女大学生作为研究对象（身高在155～182 cm，体重在42～84 kg）。为排除异常数据，基于“平均差±3σ”（σ为标准差）对样本进行异常值检测［7］，排除333%的样本，最终确定有效样本量232人。

1.2 测量项目

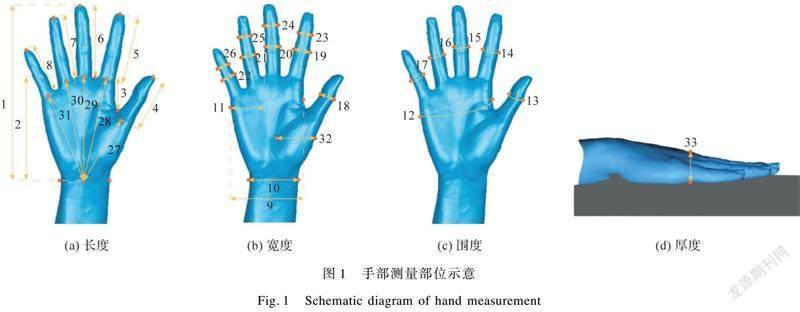
参考GB/T 16252—1996《成年人手部号型》和GB/T 5703—2010《用于技术设计的人体测量基础项目》，确定了包括手长、掌长、虎口食指叉距等33项手部测量项目，如图1所示。1—手长、2—掌长、3—虎口食指叉距、4—拇指长、5—食指长、6—中指长、7—无名指、8—小指长、9—手宽、10—手腕宽、11—尺侧半掌宽、18—拇指关节宽、19—食指近位指节宽、20—中指近位指节宽、21—无名指指近位指节宽、22—小指近位指节宽、23—食指远位指节宽、24—中指远位指节宽、25—无名指远位指节宽、26—小指远位指节宽、27—拇指根到腕中心距离、28—食指根到腕中心距离、29—中指根到腕中心距离、30—无名指根到腕中心距离、31—小指根到腕中心距离、32—大鱼际宽;12—掌围、13—拇指關节围、14—食指近位指关节围、15—中指近位指关节围、16—无名指近位指关节围、17—小指近位指关节围;33—掌厚。

1.3 三维扫描测量法

依据GB/T 23698—2009《三维扫描人体测量方法的一般要求》，实验环境相对湿度为（60±10）%，温度为（27±3） ℃。使用多功能手持3D扫描仪（EinScan，中国先临，测量精度004 mm）采集手部三维点云数据，要求被测试者手部自然张开（确保各手指间有空隙即可）且伸直［5］。扫描过程中，由于被测试者手部容易产生轻微晃动，导致三维点云存在噪点，因此对噪点进行平滑处理。此外，扫描时手部细微部位存在扫描不完整、数据缺失现象，需对孔洞部位进行填充处理，以便得到光滑完整的手部点云数据。本文将手持式三维扫描的测量方法分为以下3个步骤：

1） 辅助点、线和面建立。特征点是确定手部特征部位尺寸的关键，但在判断手部特征点时，存在人为主观判断导致测量值重现性较差。为保证重复测量的稳定性，故在确定特征点前标准化辅助点、线、面。表1为中指与手掌的辅助点—线—面的定义方法，图2为标定示意。

2） 手部特征点。根据上述步骤确定所需要的辅助点、线、面后，结合GB/T 16252—1996和GB/T 5703—2010，确定手部特征点。以中指、手掌为例，特征点定义如表1所示，特征点标定如图2所示。同理，可以确定其他手部宽度、围度特征点。

3） 手部尺寸测量。为减少三维扫描时被测试者可能存在轻微晃动影响，通过手持式三维扫描仪对手部进行3次扫描，基于处理后的手部三维点云数据，通过上述步骤方法，标准化测量方法，对33项手部特征参数进行3次测量取平均值。

2 结果与分析

2.1 典型指标选择

针对手部测量数据比较多，本文通过提取易测量且能表征手部信息的典型指标去预测掌厚等其他难以测量的手部尺寸。

2.1.1 因子分析

为减少重复和关系紧密的变量，通过主成分分析对变量进行降维［8］。先对样本进行正态分布假设检验，经检验33个变量数据呈近似正态分布。再對右手变量进行Bartlett和KMO检验，Bartlett球形检验统计量的观测值为528，概率p值接近0，显著性水平α为0.050小于概率p值，认为相关系数矩阵与单位阵有显著差异。KMO值为0.932接近于1000，根据Kaiser的KMO度量标准判定原有的33个变量适合进行因子分析。通过主成分分析由各成分的方差贡献率和累计贡献率可知，前5个主成分的特征根均大于1.000，累计方差贡献率为80.815%，说明这5个主成分能够描述人体手部形态特征，结果如图3所示。

旋转后的因子载荷矩阵，可具体定义主成分因子的类型。主成分因子1在指宽、指围等变量上有较大载荷，可定义为指宽因子;主成分因子2在掌长、指根到腕中心距离等表征手掌长度尺寸变量上载荷系数较大，可定义为掌长因子;主成分因子3在拇指长等5个指长变量上载荷系数较大，可定义为指长因子;主成分因子4在手长、掌厚等变量上载荷较大，可定义为手部横矢径比因子;主成分因子5在手宽、尺侧半掌宽变量上载荷较大，可定义为掌宽因子。综上，影响手部形态的因子主要有指宽因子、掌长因子、指长因子、手部横矢径比因子、掌宽因子。

2.1.2 相关指数最大值法

为挑选能反映手部形态特征且方便测量的指标，本文采用相关指数最大值法在各变量中选取典型指标，计算如下式所示：

式中：Rj为变量j的相关指数;rij为相关系数，j=1，2，3，…，m;i=1，2，3，…，m;m为所在因子的指标数量，选取其中相关指数最高的指标作为各类因子的代表性指标，其中相关系数可由Pearson相关分析系数矩阵得到。

根据计算结果（表2），选择手长、手宽、中指长、食指近位指关节围、无名指到腕中心距离5个变量作为典型指标。

2.2 模型构建

2.2.1 BP神经网络

针对手部特征部位尺寸较为离散且非线性的特点，本文采用BP神经网络对手部特征部位尺寸进行预测。BP神经网络采用复合函数链式法则，计算过程包括输入数据的正向传播和输出误差的反向传播，具有较强的非线性映射能力，可以逼近任意非线性连续函数［9］。

根据Kolmogrov定理设置BP神经网络手部尺寸预测模型的网络结构为5-11-1，将样本按8︰2比例分为训练集与测试集，BP神经网络参数设计如表3所示。其中输入层为手长等5个典型指标，对应输出层用Ok表示，通过手部典型指标预测手部尺寸的过程包括：结果输出计算及误差产生和权值调整阶段。

1） 结果输出计算：

式中：Ok表示第k节点的输出，k=1，2，…，r;Wjk表示隐含层第j节点输入与第k输出点之间的权值;Yj为隐含层第j节点输出;θk为第k节点的阈值。

2） 误差产生：

式中：i=1，2，…，m;dk为第k节点期望输出。

3） 权值调整：

式中：Wjk（t+1）表是经第t+1次迭代后，隐含层第j节点输入与第k输出节点之间的权值;μ∈（0，1）为神经网络学习速率。

2.2.2 线性回归模型构建

线性回归模型是利用线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析，其模型如下式所示［10］：

Y=B0+B1X1+B2X2+B3X3+B4X4+B5X5（5）

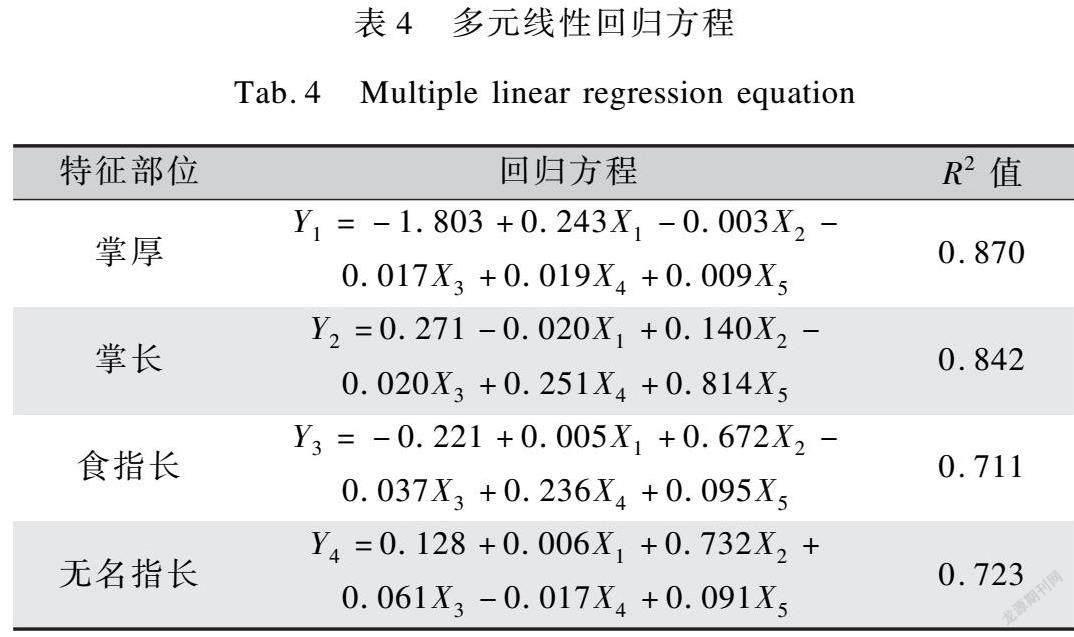
式中：B0表示常数，X1、X2、X3、X4、X5分别为手长、手宽、中指长、食指近位关节围和无名指指根到腕中心距离，B1、B2、B3、B4、B5分别为X1、X2、X3、X4、X5的系数，Y为掌厚等不易测量的手部特征部位尺寸。

本文以掌厚等28项不易测量手部特征部位为因变量，手长、手宽等5项典型指标为自变量建立多元线性回归模型。其中，掌厚、掌长、食指长、中指长4个特征部位的R2值大于0.700，分别为0.870、0.842、0.711、0.723（表4）。

2.3 预测模型对比分析

通过相关指数最大值法得到5个手部典型指标，运用BP神经网络、多元线性回归分别构建手部尺寸预测模型。并以MAE、R2和配对样本T检验Sig.值作为评判指标，将预测模型与文献［6］进行对比分析。

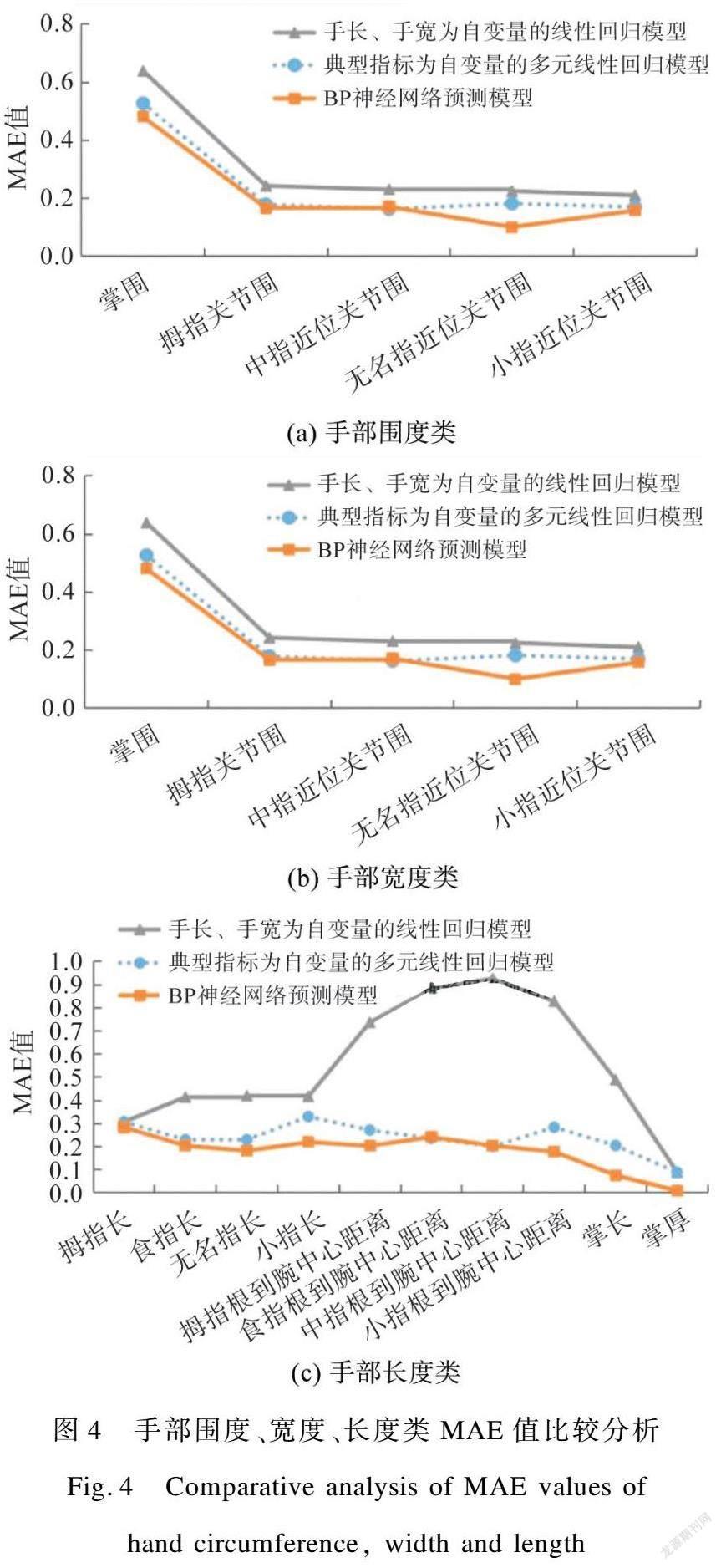
回归损失函数MAE表示预测值和观测值之间绝对误差的平均值，其值越小，预测精度越高，因此，本文使用MAE作为评判预测模型精度的指标。围度类手部特征部位尺寸预测结果如图4（a）所示，可知掌围在围度类指标中MAE最高，其中BP神经网络预测模型预测效果最好，MAE小于0.500。宽度类手部特征部位尺寸预测结果如图4（b）所示，可知手腕宽、虎口食指差距、尺侧半掌宽和大鱼际宽这4项手部特征MAE较高，主要是这4项特征部位与手部其他特征部位相关性较低有关。长度类手部特征部位尺寸预测结果如图4（c）所示，可知BP神经网络预测掌厚误差值最低，仅为0.010，以手长手宽为自变量的线性回归模型在拇指根到腕中心距离等5项手掌因子上预测效果最差，MAE最高，这是因为仅以手长手宽为预测指标，缺少手掌部分的综合信息，与手掌因子相关性较低有关。

综上可知，BP神经网络的整体预测效果较好、MAE较低、稳定性较高，相比于已有文献［6］以手长、手宽为自变量的线性回归预测模型和以5个典型指标为自变量的线性回归模型，平均绝对误差MAE分别降低了3%、2%。这与BP神经网络具有很强的非线性映射能力和柔性的网络结构有关。

R2为评判数据拟合程度指标。为进一步分析BP神经网络模型与多元线性回归模型的预测效果，本文以R2作为评判指标，R2越接近1.000，说明模型拟合程度更高。3个模型拟合结果如图5所示，可知BP神经网络模型的手部尺寸预测值与实际值之间存在较强相关性，R2平均值为0.710。以手长等5个典型指标为自变量的多元线性回归模型R2平均值为0.550，而手宽、手宽为自变量的线性回归模型R2平均值仅为0.210。说明相比于其他两个预测模型，BP模型拟合程度更高，预测效果更好。

为验证BP神经网络尺寸预测模型的准确性，本文将各手部尺寸的预测值与实际测量结果进行配对样本T检验，结果如图6所示。分析圖6可知，各配对样本之间的均值标准误差均小于0.100 mm，表明BP神经网络尺寸预测模型的预测值与实际测量值较为接近;且经配对样本T检验，除大鱼际宽、手腕宽等3项手部尺寸Sig.（双尾）小于0.050（这与大鱼际宽等其他手部特征部位相关性较低有关），其余手部特征部位Sig.（双尾）均大于0.050，即配对样本之间无显著性差异。以上分析可知，本文构建的基于数据9驱动的BP回归预测模型精确度更高，模型拟合优度较好，可通过少量、易测量的典型指标预测25项手部特征部位尺寸，有效减少手部尺寸测量项目。

3 结 论

为更有效地对手部尺寸进行测量和预测，本文构建了两个数学模型，通过三个评价指标对比分析并验证最优的预测模型，得出的主要结论如下：

1） 通过主成分分析对33项手部尺寸进行降维，获取了影响手部形态5个因子，主要有轮廓因子、手掌因子、指长因子、手部横矢径比因子和宽度因子。

2） 采用相关指数最大值法，获取了手长、手宽、中指长、食指近位指关节围、无名指到腕中心距离5个尺寸变量作为典型指标，用于其余28项手部尺寸测量。

3） 分别构建了BP神经网络预测模型和多元线性回归模型，以平均绝对误差MAE、相关系数R2和配对样本T检验Sig.值作为评判指标，对预测模型的有效性进行比较分析。结果表明，BP神经网络预测模型预测效果更好，平均绝对误差MAE值和平均相关性系数R2相比于线性回归模型分别降低了3%、提高了15.9%，且预测值与实际值无显著性差异。

参考文献：

［1］YANG Y S， ZHOU H P， SONG Y， et al. Identify dominant dimensions of 3D hand shapes using statistical shape model and deep neural network［J］. Applied Ergonomics， 2021， 96： 103462.

［2］GARCA-CCERESRG， FELKNOR S， CRDOBAJE， et al. Hand anthropometry of the Colombian floriculture workers of the Bogota plateau［J］. International Journal of Industrial Ergonomics， 2012， 42（2）： 183-198.

［3］CAKIT E， DURGUN B， CETIK O， et al. A survey of hand anthropometry and biomechanical measurements of dentistry students in Turkey［J］. Human Factors and Ergonomics in Manufacturing & Service Industries， 2014， 24（6）： 739-753.

［4］VERGARA M， AGOST M J， GRACIA IBANEZ V. Dorsal and palmar aspect dimensions of hand anthropometry for designing hand tools and protections［J］. Human Factors & Ergonomics in Manufacturing & Service Industries， 2017， 28（8）： 17-28.

［5］FAN D Y， MA X M， WANG L J. Hand measurement and analysis based on image and mark watershed algorithm［J］. International Journal of Clothing Science and Technology， 2021， 33（5）： 822-842.

［6］范丹镱， 马希明， 王利君. 基于聚类分析的浙江青年男性手形分类与号型优化［J］. 丝绸， 2021， 58（2）： 53-58.

FAN Danyi， MA Ximing， WANG Lijun. Hand shape classification and size optimization for young men in Zhejiang based on cluster analysis［J］. Journal of Silk， 2021， 58（2）： 53-58.

［7］JIN J F， YANG Y C， ZOU F Y. Developing an intelligent model for the construction a hip shape recognition system based on 3d body measurement［J］. Fibres & Textiles in Eastern Europe， 2016， 24（5）： 110-118.

［8］TADESSE M G， CHEN Y， WANG L C， et al. Tactile comfort prediction of functional fabrics from instrumental data using intelligence systems［J］. Fibers and Polymers， 2019， 20（1）： 199-209.

［9］李萍， 曾令可， 稅安泽， 等. 基于MATLAB的BP神经网络预测系统的设计［J］. 计算机应用与软件， 2008， 25（4）： 149-150.

LI Ping， ZENG Lingke， SHUI Anze， et al. Design of forecast system back propagation neural network based on MATLAB［J］. Computer Applications and Software， 2008， 25（4）： 149-150.

［10］ZHANG B W， SONG J X， ZHAO S N， et al. Prediction of yarn strength based on an expert weighted neural network optimized by particle swarmoptimization［J］. Textile Research Journal， 2021， 91（23/24）： 2911-2924.

Abstract： In the anthropometric process， muscle tissues stretch and contract to varying degrees， which results in poor reproducibility of measurement results and errors in measurement. While hands are an important part of human body， in the process of hand measurement， involuntary muscle movements and soft tissue deformation occur in the hand， and the size of the hand needs to be measured in a large and fine way， which is not easy to measure. Methods for collecting correct measurements of the characteristic parts of the hand can also be challenging. At present， hand size measurement is divided into contact manual measurement and non-contact measurement. Contact manual measurement preparation process and measurement process are time-consuming， and the measurement result is easily affected by the subjective factors of the measurement personnel. Non-contact measurement includes two-dimensional （2D） image measurement and three-dimensional （3D） scanning， and image measurement is limited by the angle and position of the photograph. Nevertheless， the measurement cost of 3D scanner is high and its popularity is not high. Therefore， it is necessary to explore more convenient methods of hand size measurement.

In view of the problem of multiple and complicated hand size measurement items， we proposed a data-driven mathematical model to predict the hand size. The dimensions of 33 characteristic parts of 232 female college students hands were collected by 3D scanner， and principal component analysis （PCA） was used to extract five characteristic factors affecting hand morphology， i. e. finger width factor， palm length factor， finger length factor， transverse sagittal diameter ratio factor for the hand and palm width factor. Five typical indexes including hand length， hand width， middle finger length， proximal knuckle circumference of index finger， and distance from ring finger to wrist center were obtained by the correlation index maximum method. BP neural network and multiple linear regression were used to construct hand size prediction models. The aim of this study was to use a small number of indicators relatively easy to measure to build data-driven prediction models， so as to get more hand size information. The results show that the mean absolute error （MAE） of the BP neural network prediction model is lower， the degree of fit is better compared to the multiple linear regression hand size prediction model， and the MAE is reduced by 2% respectively， the degree of fitting R2 increases by 0.156， the Sig. values for 25 hand sizes are greater than 0.050， the prediction effect is satisfactory and the stability is high. The results can provide reference for predicting other hand sizes from a small number of easily measured hand sizes.

This paper provides an objective method for the measurement of hand characteristic dimensions， but there are still some limitations， and comparative research and classification research can be carried out by expanding the region and age of the experimental subjects. In addition， optimizing the BP neural network prediction model by the algorithm can further improve the accuracy of hand size prediction models， and provide reference for predicting other hand sizes from a small number of easily measured hand sizes.

Key words： measurement of hand dimensions; correlation index maximum method; multiple linear regression; BP neural network; prediction model