基于组合模型的卷烟市场需求预测研究
朱峰 高林


[提要] 本文立足于卷烟营销实际,综合运用多元线性回归、ARIMA、GM等预测模型,对卷烟市场需求量进行预测分析。
关键词:市场需求预测;多元线性回归;ARIMA;GM
中图分类号:F713.54 文献标识码:A
收录日期:2016年11月29日
一、前言
随着烟草行业市场化取向改革的逐渐纵深,科学合理预测卷烟市场需求越来越受到重视,如何更好地发挥需求预测的导向作用,提高市场把握能力,已成为市场化改革的重要课题。
李铖瀚(2014)针对目前烟草企业全国销售数据来源多、数据规模庞大等特点,在分析Hadoop平台的可行性之后,对各省市各规格卷烟的销售数据进行处理,建立符合卷烟市场特征的时间序列销量预测模型。宁旭(2014)以西双版纳州烟草公司为例,在对原始数据如销售数据、库存测算数据等进行分析的基础上,构建预测模型,并对将卷烟需求预测的数据快速应用到卷烟投放工作进行实证研究。梁红梅(2015)采用“多元回归模型”和“二次指数平滑法”对云烟销售情况进行预测,并通过两种不同预测方法结果的比较,综合选定预测模型。熊莹(2015)通过对市场需求预测工作和货源供应和投放的探索,为准确把握消费者真实需求,稳定卷烟市场提供参考依据。鲁萍(2016)以当前的供给侧改革为背景,对现在烟草真实的需求市场,以及如何通过采取一系列的措施建立起完善烟草市场需求体系,最后为烟草市场实现供给侧改革提供保障。
上述研究通过各种方式对卷烟市场展开预测,但仍难以形成市场的精准判断,预测结果的实际指导价值也大打折扣。本文以组合预测思想为基础,经过实际经营数据的分析,找出最优的市场需求预测方法,以期实现市场需求的精准把握。
二、预测方法
(一)多元线性回归分析。在现实问题研究中,因变量的变化往往受几个重要因素的影响,此时就需要用这些影响因素作为自变量来解释因变量的变化,这就是多元回归亦称多重回归。当多个自变量与因变量之间是线性关系时,所进行的回归分析就是多元性回归。
(二)ARIMA。ARIMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。其中,ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归,p为自回归项;MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数。ARIMA模型根据原序列是否平稳以及回归中所含部分的不同,包括移动平均过程(MA)、自回归过程(AR)、自回归移动平均过程(ARMA)以及ARIMA过程。
(三)GM。灰色模型(GM模型),是指通过少量的、不完全的信息,建立灰色微分预测模型,对事物发展规律作出模糊性的长期描述的一种预测方法。GM模型的基本思想是用原始数据组成原始序列(0),经累加生成法生成序列(1),它可以弱化原始数据的随机性,使其呈现出较为明显的特征规律。然后对生成变换后的序列(1)建立微分方程型的模型,即GM模型。GM模型最常见的形式为GM(1,1),表示1阶的、1个变量的微分方程模型。
三、模型的构建
本文以青岛市年度数据为例,对预测模型进行构建。
(一)多元线性回归模型。卷烟销售不但受其自身历史销售数据的影响,还容易受到经济、社会、人口等相关因素的影响。为考察卷烟销售受历史影响的期数及受经济、社会、人口等因素的影响指标,我们首先进行相关性检验。
1、相关性检验。利用SPSS软件进行相关性检验,结果可知:(1)销量主要受到其前两期数据影响,又由于前两期数据之间的相关性较高,因此可以仅选前一期作为影响滞后数据序列;(2)卷烟销售与经济、社会、人口等方面指标均表现出负相关效应,其中GDP、城镇居民人均可支配收入、城镇居民人均消费支出、社会从业人员、社会消费品零售总额等指标与卷烟销售的负相关性表现相对明显,相关系数绝对值在0.5以上,其他指标相对较小。因此,选择的指标为:GDP、城镇居民人均可支配收入、城镇居民人均消费支出、社会从业人员、社会消费品零售总额。从指标之间的独立性分析,所选取的各指标之间相关性尽管较大,超过0.9,没达到1,因此可以认为他们之间不具有线性关系,具有独立性。
2、多元线性回归预测模型的构建。针对相关性检验结果可知,影响因变量卷烟销量的主要因素为:滞后一期的卷烟销量、GDP、城镇居民人均可支配收入、城镇居民人均消费支出、社会从业人员、社会消费品零售总额。据此,利用SPSS软件进行回归分析,可得如下结果:
卷烟销量(万箱)=41.03+0.04×Y1+6161.437×GDP-64178.185×社会从业人数-8782.487×社会消费品零售总额
(二)ARIMA模型。针对卷烟销售数据,通过SPSS软件进行ARIMA预测分析,结果如下:
1、数据序列平稳性分析。首先,我们构建数据序列图,可以看出,销量序列不具有明显的周期性和季节性,但表现出较为明显的平稳增长趋势,这表明该序列无利群点和缺失值。进一步从直方图来看,样本的平均值为86,467,560.875条(约34.59万箱),标准差为3,708,012.95302,样本容量为8。
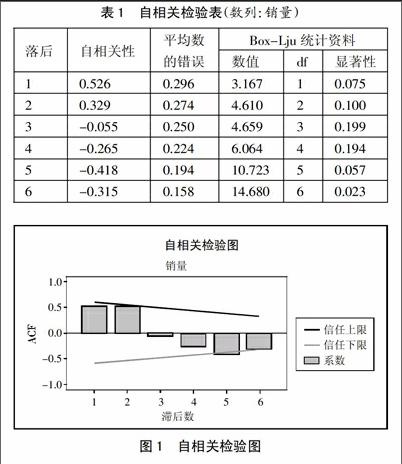
2、数据序列自相关性检验。对数据序列进行自相关性分析,结果如表1、图1所示。(表1、图1)由图1可知,该时间序列的自相关系数按一定的衰减趋势收敛到零,该序列是平稳时间序列。由图2可知,在SPSS给出了不同滞后期的样本自相关系数值、样本自相关系数的标准误差以及Box-Ljung统计资料,都可以说明该序列不是白噪声,是具有自相关性的时间序列,可以建立模型。(表2、图2)
3、ARIMA建模。针对上述数据序列,运用SPSS进行ARIMA建模,结果如表3、表4所示。(表3、表4)由表3、表4可知,模型的拟合优度BIC的值为32.183,并且模型的参数估计中常数项为85,315,898.67条(约34.13万箱),对数据的分析比较恰当。
(三)GM模型
1、数据预处理。对上述销量数据,以2007年为基期,进行标准化处理,结果如表5所示。(表5)
2、级比检验。对销量标准化数据,通过级比检验公式可以计算出?滓(k):
3、建模。根据销量标准化数据,利用matlab编程分析,可以估算出估计参数:
从而在以2007年为基期情况下(即2007年为第1年,k=1),第k+1年销量的GM预测模型为:
销量(k+1)=32×{(1-exp(-0.0146))×(1+1.0226/0.0146)×exp(0.0146×k)}
四、预测结果比较
根据以上构建的三种预测模型,分别对2015年的销量进行预测,结果如表6所示。(表6)
针对表6展示的三种模型预测结果,专家组可以根据三种结果进行比较分析,推测2015年的卷烟销量值。假如专家组采用均值法,则2015年的卷烟销量预测值为:37.65万箱。结合2015年实际卷烟营销数据进行比对,预测数据较为合理。
卷烟需求预测是在新形势下,烟草公司需要按照一定的工作程序和预测方法,对一段时期内的卷烟需求所做出的推测和判断。它是卷烟企业了解市场真实需求并按照市场真实需求组织货源的一个关键环节。预测是否准确决定了货源的组织能否满足市场消费需求,也在一定程度上决定了企业的经营利润,反映了烟草商业企业的经营能力。
需求预测的方法很多,要非常熟练掌握这些预测方法,同时针对不同情况准确选取预测方法更为重要。卷烟市场需求量的变化不单单是随着时间的变化而变化,还会受到其他很多因素的影响,为此在进行卷烟市场需求量预测时,尽量选用贴近现实的需求预测模型,可以为准确的预测出卷烟市场的需求量提供有力帮助。
主要参考文献:
[1]李铖瀚.基于海量数据的销售预测研究与实现[J].浙江理工大学,2014.
[2]宁旭.地市级局卷烟需求预测模型的构建与应用研究[J].昆明理工大学,2014.
[3]梁红梅.组合预测方法在云产卷烟需求预测中的应用研究[J].昆明理工大学,2015.
[4]熊莹.如何寻求卷烟市场需求与货源组织和供应的基本平衡点[J].中国烟草学会2015年度优秀论文汇编,2015.

