核心素养视域下的初中数学推理能力培养

陈礼军

(福建技术师范学院附属中学,福建 福州 350301)

在科教兴邦的教育大环境下,检验一个人才的标准不只是高分,更重要的是能力和素养.数学核心素养的提出更是引发了人们的热议,时至今日仍旧是一个十分值得关注的话题.2022年版的《义务教育数学课程标准》中,进一步明确要求教师要注重培养学生形成推理能力,还在“数与代数”部分凸显了推理能力的培养.提倡教师结合学生的推理能力发展现状,建立有效的教学策略,培养学生的逻辑思维及数学推理能力,形成数学推理素养,这既是落实核心素养育人目标的需要,也是促进学生终身发展的需求.

1 推理能力概述

在《辞海》中对“推理”一词进行了解释,其指出推理是推理思考方式之一,由已知推断结论,或由结果反向地推导出已知的理由,是人们在解释因果关系、说明现象过程中经历了演绎、归纳、类比等思考活动[1].从解释中可以看到推理能力是依靠学者敏锐的分析思考,而后快速判断并明白问题的核心,达到在比较短的时间内做出合理选择的思维能力表现.推理能力的表现有以下几种形式:第一,演绎推理.数学的演绎推理是数学界公认的一种绝对准确的判断过程,它从一般到特殊的推理方式,如,A是B,C是A,所以B是C.在演绎推理的过程中学生一般会经历分析、综合、抽象、概括等过程,这是科学论证的一个基本组成形式,同时也是数学严谨性特征的体现.第二,类比推理[2].崔清田认为类比推理就是依据两个或两个以上的对象,其某些属性上存在相同点,推理出它们在其他属性上也相同.可见,类比推理的过程就是从两个或两类及其以上的对象研究中,发现它们存在着相同点或相似性,进而根据已知特征提出另一个或另一类对象也具备这个特征的推理过程.第三,归纳能力.波利亚曾指出,归纳是通过观察和组合特殊的例子来发现普遍现象的过程,是从特殊到一般的升华,需要从经验和概念出发,按照某种法则进行了前提与结论之间的关系推理.

2 核心素养视域下的初中数学推理能力培养策略

2.1 大胆推理小心验证,培养演绎推理能力

数学新课标要求教师要让学生具备分析与解决问题的能力,教师就要着重培养学生提出问题与发现问题的能力,鼓励学生尝试解决和分析问题与已有知识的联系.就是说发现与提出问题比成功解决一个问题更为重要.教师在数学教学过程中,应引领学生经历提出问题、发现问题、分析问题以及解决问题的全过程,促使学生经历知识发现的过程,参与到完整论证的探索活动之中,学会猜想,敢于创造,在猜想与验证中获得演绎推理能力的锻炼[3].

以《平行四边形的性质》一课教学为例,在教学初始环节教师先让学生回顾了平行四边形的定义,紧接着提出问题:根据平行四边形的定义,我们可以知道平行四边形有着两组对边平行的特点,那么除此之外其还会有其他的性质吗?问题的提出,可以推动学生大胆猜想,一些学生开始猜想:两组对角分别相等.这就是一种大胆的猜想,是建立在“两组对边平行”性质基础上对了另一种性质的合理推断,为了验证这一猜想是否正确,教师可以与学生们共同用工具(如量角器)实践测量,在多次测量中验证猜想,最终得出结论:平行四边形的对角相等.在得出结论后,教师应继续要求学生通过画图的方式,进一步证明结论的正确性,如画出图1,ABCD,已知这个四边形是平行四边形,那么根据“对边平行”的定义,即可得出AB∥CD,AD∥BC,由AB∥CD,可以证出∠A+∠D=180°,相同原理的可以证出∠C+∠D=180°,根据“同角的补角相等”,得出∠A=∠C,同理得到∠B=∠D,证得平行四边形的对角相等.在这个过程中,学生们大胆地提出了猜想,在经过小心的论证之后,探索出了平行四边形的又一个性质,接着思考还有别的方法推导对角相等吗?可以带领学生在验证与证明中,获得演绎推理能力的发展.

图1 平行四边形ABCD

2.2 联系已知找到共性,培养类比推理能力

类比推理是数学推理能力的重要组成,通过对现阶段的初中生推理能力发展情况分析,发现许多学生对知识的横向对比都偏弱,推理能力的类比可见一般,也就是说学生在数学学习中难以从一类事物的研究中所获得的经验总结,去推导出其他相似的事物也应该存在的相近特性.究根到底学生在研究推理中经常忘记已知条件和已掌握的数学经验的条件之间的相似之处.在建构主义理论中指出,人不断将刚接触的新知识整合到自己旧知识体系中,才会逐步完整的知识体系,弄清楚新旧知的共性,如此学生的新知学习就会建立在类比旧知识基础上,学生的类比推理就可以自然而然地建立起来了[4].

如在《角的比较与运算》的这部分内容教学中,需要学生掌握的知识点主要有角的大小比较、角的和差以及角的平分线,这三个关于角的新知识点学习与线段的大小比较、线段的和差以及线段的中点是一一对应的.实际上,从图形上看,线段与角之间存在着一定的几何相似之处,例如线段和角都可以度量,线段和角都可以叠合,还都是轴对称图形,因此通过线段与角的性质和共同点研究,推断出二者的研究方法或一致不无道理,那么此时引领学生从研究线段的方法入手,进行角的比较与运算新知的研究也就顺理成章了.在这个过程中,教师可以通过提问的方式,引发学生的类比推理,如:(1)在线段的学习中,我们都研究了线段的哪几个方面内容?(2)线段与角都是初中最基本的轴对称图形,你能否从线段的研究中得到启示,思考我们应该从哪几个方面去考虑角的有关问题的研究?(3)能不能从线段大小的比较方法类比角的大小的比较?(4)线段的中点与角的平分线研究有什么相似之处?

利用已知的线段研究方法推理出角的新知,可以保障学生在数学新知推理中做到思维有序、条理清晰,引领学生从中找到线段与角在研究方法上的共性,进而类比得出的三等分线的定义.

2.3 细化概念融会贯通,培养归纳推理能力

数学概念的理解是初中生学好数学的根本,所以一线教学的教师应始终都要非常重视数学概念的剖析,弄清数学概念对于学生其他部分的数学知识学习以及知识运用能力发展是至关重要的.正确地处理好概念教学的讲解,离不开设计能够引发学生推理的数学情境,巧妙地引入概念,不仅能够降低学生对抽象数学概念本身的理解难度,还有助于学生探索与分析数学概念知识的延伸,从中总结的知识,将形成重要的归纳推理能力和数学抽象能力.

以《有理数的乘方》的概念教学为例,教师可以创设情境引出本节课学习的主题,将“3×3”“3×3×3”分别写成“32”“33”,提出问题:那么,3×3×3×3×3要怎样表示更为简洁呢?学生们从给出的案例中写出:35,教师追问:这里面的3和5分别代表什么?接着我们还可以提出a·a·a·a·a要如何表示呢?如果是m个a相乘,又该如何表示呢?在整个教学过程中,教师从学生熟悉的图形面积与体积计算问题出发,引领学生在列出式子、观察式子寻找规律中,让学生初步地掌握相同因数连续相乘的简单表示方法.认识到“3”是因数,“5”表示的是相同因数的个数,进而推理出将“3”“5”分别换成“a”“m”,即得出am.为了对底数,指数更加清楚地认识,比如对于-14与(-1)4又有什么区别,看似很简单,可是学生在练习中极容易出现计算错误的问题.因此在教学中,老师应进一步细化概念,思考算式-(1×1×1×1)与(-1)×(-1)×(-1)×(-1)用乘方如何表示,它们计算结果一样吗?这样思考对底数,指数将会有清晰的思维,再给出计算-23与(-2)3,-12021与(-1)2021,-12022与(-1)2022,-12n与(-1)2n,-12n+1与(-1)2n+1些题目给学生思考,所得到结果又怎样?促使学生在数学概念的学习中,经过从特殊到一般的归纳过程,学生的归纳推理能力无形之中得到了锻炼.

2.4 开展变式练习活动,提升推理应用能力

数学推理应用能力的培养,其关键在于学以致用,促使学生运用严谨、灵活的思维解决问题,促使学生从某一个问题分析推理以及解决中,掌握同一类问题的解决方法,当学生再次遇到此类数学问题的时候,就可以迎刃而解了.数学问题的设计有着“换汤不换药”的特点,一些看似复杂的情境,看似困难的问题,实际上都是从简单的情境、简单的问题中升级变化而来的,只要学生掌握了其中的核心知识点,就能够从复杂的问题中推理出本质,进而灵活地运用所学的数学公式定理,轻松地解答问题,促使学生在变式训练中获得数学应用能力的提升,升华推理能力培养的教学价值[5].

如图2,平行四边形ABCD所示,在平行四边形ABCD中,AD=AB,∠BAD=60°,边CB、DC上分别有点E、F,且∠EAF=60°,(1)求证:∠BAE=∠CEF;(2)若边CB、DC的延长线上分别有点E、F,其他条件不变,如图3,四边形ADFE,让学生猜想∠BAE与∠CEF的数量关系如何?证明你的猜想. 在这道题目中第一个问题让学生求证∠BAE和∠CEF两个角是相等的,第二个问题是在其他条件不变的情况下,点E、F在ABCD的边的外延长线上,进而说明∠BAE与∠CEF的关系,学生在第一问的解答时可以获得提示,很容易猜到∠BAE与∠CEF相等,促使学生在推理与验证中强化了问题解答能力,能够由此及彼地解答问题,寻找解决问题的方法,这样学生的数学推理能力以及应用能力都得到了一定程度上的进步.

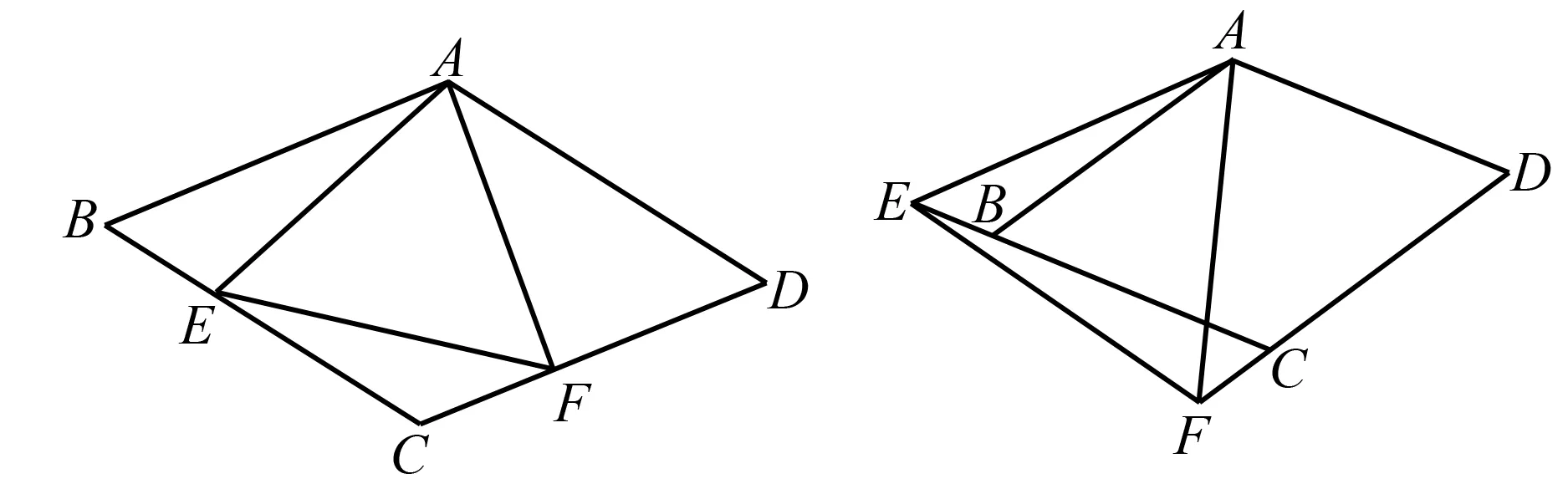
图2 平行四边形ABCD 图3 平行四边形ADFE

总之,推理能力是初中生数学核心素养形成中的主要组成部分,教师应在数学教学中注重推理能力的培养,为学生提供更多参与推理验证的机会,能够结合初中生的思维发展规律以及数学学习情况,总结出一套行之有效的教学方案,为学生的数学推理能力培养提供助力,以促进数学核心素养的生成.