利用折纸活动提高初中生几何思维水平的教学策略

余兴梅

(新沂市实验学校,江苏 新沂 221400)

折纸活动一直备受数学教师和中考命题者的青睐.笔者结合自己的教学实践,谈谈利用折纸活动提高初中生几何思维水平的一些感受.

1 折纸活动在初中几何教学中的优势

数学学习的过程是一个合作探究交流、不断生成的过程.在师生互动、生生互动这样一个有趣的互动合作的过程中学习,学生在做中学,在操作中学,在交流中学,不但可以培养学生的动手操作能力,还能培养学生的合作学习能力以及语言表述能力.特别是在折纸活动中,让每位学生都积极地参与,真正通过自我参与、动手操作来感受获取新知的成就感,进一步提升在探究新知过程中对几何思维能力的培养,形成教学模型以夯实教学而提升学生的数学素养[1].

初中数学学习中的折纸不仅仅是一种单纯的手工制作,更重要的是借助折纸培养学生几何思维的一个创新活动.在学生独立动手操作与小组合作互动学习活动中有效地培养学生的创造性思维,开拓学生创新的综合思维能力.在折纸后会出现许多精彩的问题,在解决这些问题的过程中让学生经历如何将实际问题转化成数学问题,经历从猜想、再到求解验证的数学学习过程,培养学生对数学知识的综合应用的能力,提高学生的几何思维水平.

2 折纸活动在初中几何教学中的有效策略

2.1 借助折纸活动得到几何概念,帮助学生理解概念

如图1,在《等腰三角形》的教学过程中,我们采用如下的折纸过程:让学生拿出一张长方形纸片,按照如图的要求进行折纸,然后用剪刀裁去下面的一部分,再把裁剪后的直角三角形展开．所得到的三角形是什么形状的三角形呢?

图1 纸片折剪图

通过纸片的折剪的过程,学生很容易得到△ABC是等腰三角形——此时学生对于等腰三角形的概念——有两边相等的三角形叫做等腰三角形,理解得就非常透彻,从而对等腰三角形的判定也有了初步方法.

2.2 借助折纸活动探究几何定理,帮助学生理清思路

如图2,在探究《等腰三角形的性质》的教学过程中,我们采用如下的“折纸”过程:

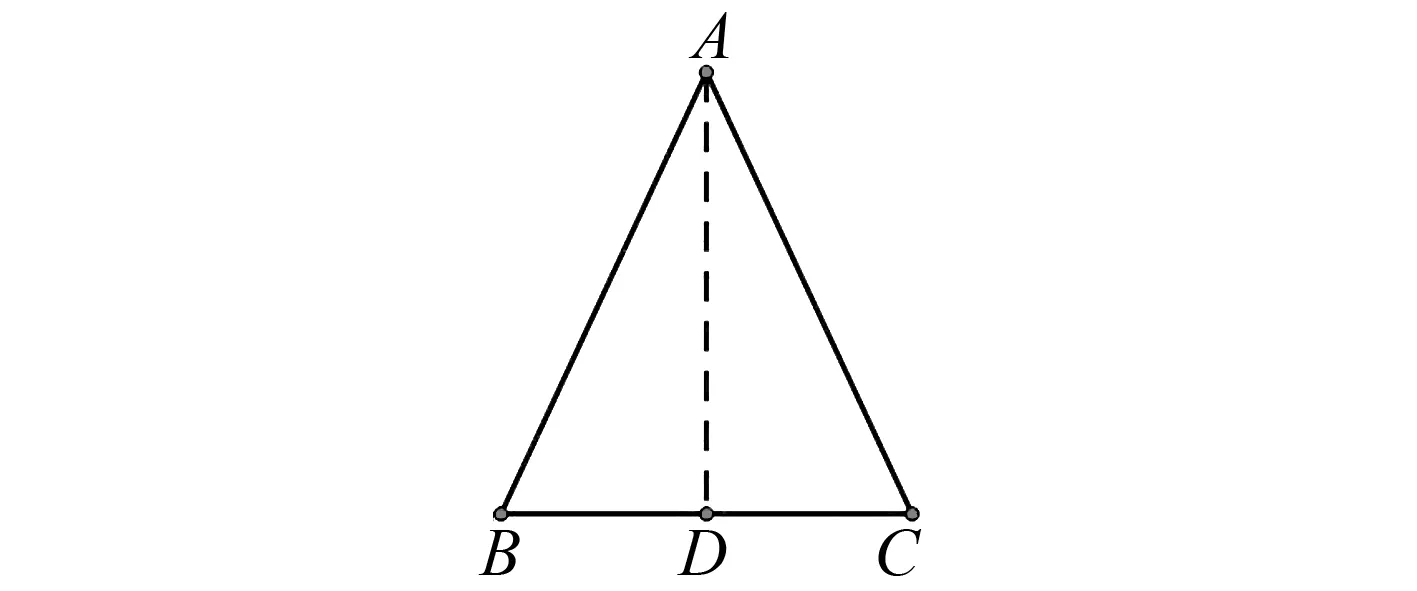
图2 等腰△ABC对折图

将等腰△ABC对折,请大家思考:

题1 等腰△ABC是轴对称图形吗?如果是,其对称轴是什么?

通过刚才的折纸,你能用文字语言将你们的发现概括出来吗(小组交流派代表发言)?

最后教师引导学生进行归纳总结:(1)等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴;(2)等腰三角形的两个底角相等(简写成“等边对等角”);(3)等腰三角形的顶角平分线、底边上的中线、底边上的高线相互重合(简写成“三线合一”).

刚才通过折纸我们只是停留在几何直观和操作层面,数学学习更要重视结论的准确性的证明,借助于刚才的折纸提供的思路,你能证明等腰三角形的两个底角相等吗?

题2 已知:如图3,△ABC中,AB=AC.求证:∠B=∠C

图3 △ABC

解法一作顶角的平分线AD(利用SAS证明△ABD≌△ACD)除了可以得到∠B=∠C,从而说明“等边对等角”,同时也可以得到BD=CD,∠ADB=∠ADC=90°,即AD⊥BC,从而说明“三线合一”.

解法二作底边的中线AD(利用SSS证明△ABD≌△ACD),除了可以得到∠B=∠C从而说明“等边对等角”,同时也可以得到∠BAD=∠CAD,∠ADB=∠ADC=90°即AD⊥BC,从而说明“三线合一”.

解法三作底边的高线AD(利用HL证明△ABD≌△ACD),除了可以得到∠B=∠C,从而说明“等边对等角”,同时也可以得到∠BAD=∠CAD、BD=CD,从而说明“三线合一”.

如果没有上面的折纸过程,学生很难想到本题中辅助线的添加,但是通过上面折纸给学生提供了本题的解题思路——学生很容易想到添加辅助线,将要证明的两个角等转化在两个三角形中,借助于三角形全等来解决问题,在证明结论(2)的同时也将结论(3)证明出来,这就培养了学生通过动手操作和转化的能力,采用一题多证的方法解决问题,更好地提高了学生的几何思维水平.

2.3 借助折纸活动进行探究,启迪学生发散思维.

问题:请同学们拿出一张三角形的纸片,你能通过折纸得到一个等腰三角形吗?谈谈你的折法.

学生1:如图4,折叠纸片使得点B与点C重合,得折痕MN交边AB与点D,连接CD,则△BCD就是等腰三角形.理由是折痕MN是边BC的垂直平分线,所BD=CD,所以△BCD是等腰三角形.

图4 三角形纸片折叠图① 图5 三角形纸片折叠图② 图6 图5变式图1

学生2:如图5,折叠纸片使得边AC与BC重合,得折痕CD交边AB与点D,再过点D画DE∥BC交边AC与点E,则△DCE就是等腰三角形.理由是因为折叠纸片使得边AC与BC重合,得折痕CD,则∠BCD=∠ACD,又因为DE∥BC,所以∠BCD=∠EDC,从而得∠ACD=∠EDC,所以DE=CE,所以△DCE是等腰三角形.

变式(1):请同学们拿出一张平行四边形的纸片,你能通过折纸得到一个等腰三角形吗?谈谈你的折法.

学生3:如图6,折叠纸片使得边AD与CD重合,得折痕DE交边BC与点E,则△DCE就是等腰三角形.理由是因为折叠纸片使得边AD与CD重合,得折痕CD,则∠ADE=∠CDE,又因为AD∥BC,所以∠ADE=∠DEC,从而得∠CDE=∠DEC,所以DC=CE,所以△DCE是等腰三角形.

变式(2):请同学们拿出一张长方形的纸片,你能通过折纸得到一个等腰三角形吗?

谈谈你的折法.

学生4:如图7,沿对角线BD折叠纸片,点A落在点E处,

图7 图5变式图2 图8 图5变式图3 图9 学生6折叠图

则重叠部分△DBF就是等腰三角形.

理由是:因为折叠纸片△ADB与△EDB重合,则∠ADB=∠EDB,又因为AD∥BC,所以∠ADB=∠DBC,从而得∠EDB=∠DBC,所以DF=BF,所以△DBF是等腰三角形.

变式(3):请同学们拿出一张长方形的纸片,你能通过折纸得到一个等边三角形吗?谈谈你的折法.

学生5:如图8对折纸片得折痕EF,再折叠纸片使得点A落在折痕EF上点N处,则△ABN就是等边三角形.理由是因为对折纸片得折痕EF,则EF是边AB的垂直平分线,所以AN=BN,又因为折叠纸片使得点A落在折痕EF上点N处,所以AB=BN,从而得AN=BN=AB,所以△ABN是等边三角形.

变式(4):请同学们拿出一张长方形的纸片,你能通过折纸得到一个菱形吗?谈谈你的折法.

学生6:如图9折叠纸片使得点B与点D重合得折痕MN,分别交边AD与BC于点M、N,连接BM和DN,则四边形BMDN就是菱形.理由是因为折叠纸片使得点B与点D重合得折痕MN,则MN是BD的垂直平分线,所以MN⊥BD,OB=OD,又因为AD∥BC,所以∠ADB=∠DBC,且∠DOM=∠BON,所以△DOM≌△BON,可得OM=ON,所以四边形BMDN就是菱形.

通过本题的折纸活动,多次变换纸片的形状同时也变换所得到的几何图形的形状,在变换的过程中,感受基本图形的构成,逐渐提炼出数学的本质,积累数学活动过程中的经验,提升了学生的几何探究能力和发散创新思维能力.

3 折纸活动教学中几点建议

3.1 利用几何画板辅助教学

利用几何画板教学时,可以将几何图形的折叠过程清晰地演示出来,让学生更直观地观察到变化过程,深入地理解变化过程中哪些量在变化,哪些量不变化,充分理解折叠前后的变化过程,从单纯的抽象直观的概念思维逐渐转化成更具体更加形象丰富的几何思维.

3.2 加强小组合作交流探究

在平时的课堂教学中,有很多老师不太注重学生动手操作能力的培养,习惯于“满堂灌”,更不会组织学生进行小组合作交流探究,让学生充分感受数学结论的发现过程以及思维的培养.所以在平时的教学中,我们要选取和折纸相关的教学内容,提倡学生在实践中先学会动手折纸操作,交流实践经验,总结实践方法,以点带面,让折纸真正成为初中几何实践教学的一项重要活动.