最大卓越周期估算震级方法的优化研究

赵庆旭,王延伟,刘 娟,莫红艳,曹振中

(桂林理工大学 广西岩土力学与工程重点实验室,桂林 541004)

0 引言

随着社会经济的发展,城市化进程的加快,地震造成的损失逐渐增加。依照目前的科学技术,短期内预测地震是不可行的,但是可以利用地震预警系统(Earthquake Early Warning system,EEWs)来减轻人员伤亡和减少次生地震灾害的发生[1]。目前,EEWs已被认为是一种有效减轻地震灾害的方法[2],已有多个地震多发国家或地区已经或正在建设地震预警系统,如日本、墨西哥、美国、罗马尼亚、土耳其、意大利、中国和伊朗等[3-11]。EEWs主要依据震级的大小来评估地震对目标区域的影响程度和范围,因此,如何从一个正在发生的地震事件中估算出震级大小,是研发地震预警系统中需要解决的关键难题之一。

1 数据选择及处理

图1 强震动记录随震级、震源距和震源深度的分布(每个点代表一条地震动记录)Fig. 1 Distribution of magnitude,hypocentral distance and depth of strong motion records (each point represents a ground motion record)

2 震级估算方法

2.1 最大卓越周期

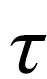
(1)

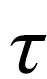
2.2 平均卓越周期c

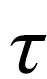
(2)

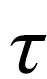
2.3 估算震级的经验公式

(3)

式中：M是震级,a和b是待定的回归系数。在利用不同时长初至P波估算震级时,需要采用相应时长初至P波的回归系数。

3.1 滤波频率范围的优化

(a)未进行滤波,记为“F0”。

(b)3 Hz低通滤波[12,18,25,42],记为“F1”。

(c)0.075～3 Hz带通滤波[31],记为“F2”。

(d)0.075～10 Hz带通滤波[14],记为“F3”。

(e)0.075 Hz高通滤波[30],记为“F4”。

(f)10 Hz低通滤波[12],记为“F5”。

(g)0.001 Hz高通滤波[43],记为“F6”。

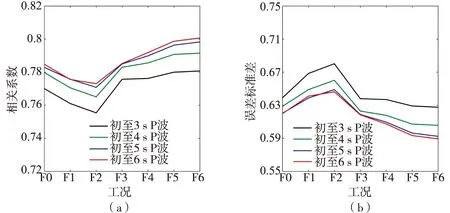
图2 不同滤波范围得到的与震级的相关性(a)和估算震级的误差标准差(b)Fig. 2 Correlation between with different filter ranges and magnitude (a) and standard deviation of estimated magnitude error of with different filter ranges (b)

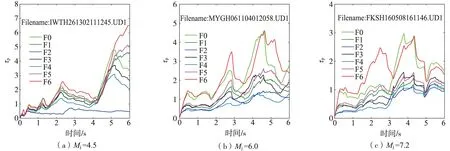
图3 不同震级地震的初至6 s P波经不同滤波范围计算出的pFig. 3 p calculated by initial 6 s P wave of different magnitude events with different filter bands

3.2 滤波阶数的优化

图4 不同滤波阶数得到的与震级的相关性(a)和估算震级的误差标准差(b)Fig. 4 Correlation between with different filter poles and magnitude (a) and standard deviation of estimated magnitude error of with different filter poles (b)

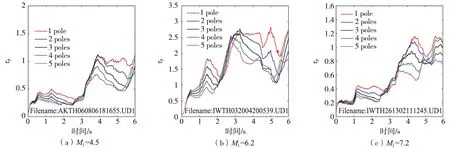
图5 不同震级地震的初至6 s P波经不同滤波阶数滤波器计算出的pFig.5 p calculated by initial 6 s P wave of different magnitude events with different filter poles

3.3 平滑系数的优化

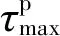
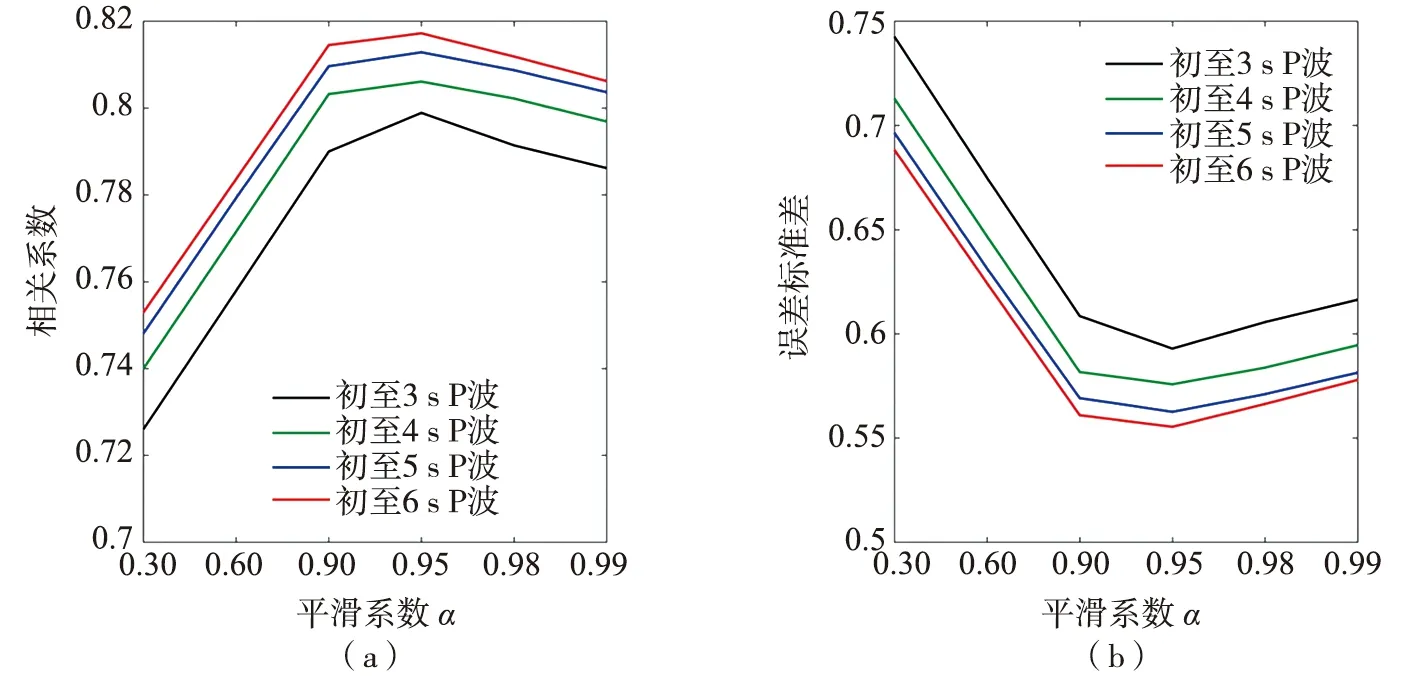
图6 不同平滑系数的与震级的相关性(a)和估算震级的误差标准差(b)Fig. 6 Correlation between with different smoothing coefficients and magnitude (a) and standard deviation of estimated magnitude error of with different smoothing coefficients (b)

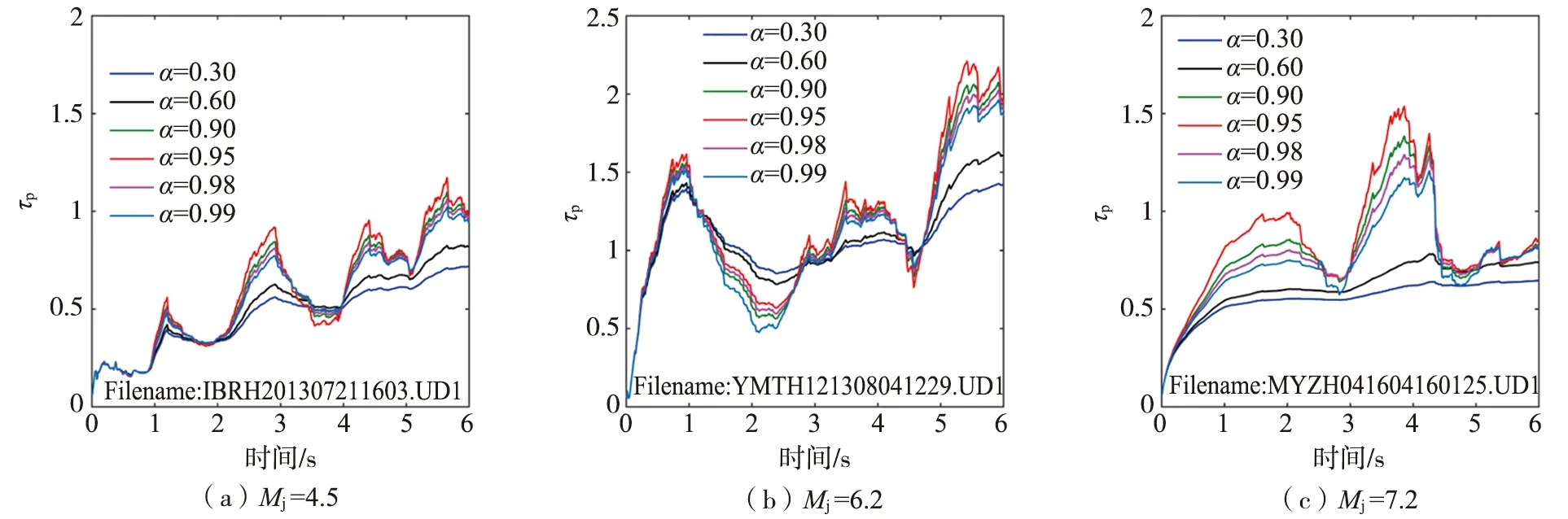
图7 不同震级地震的初至6 s P波经不同α取值计算出的pFig.7 p calculated by initial 6 s P wave of different magnitude events with different α values

4 基于日本强震动记录的震级估算效果测试

4.1 初至3 s P波时最优化的震级估算效果

注：图中每一个点代表一条地震记录1)。实线代表拟合直线2)。虚线表示±标准差3)。R为相关系数4)。a和b为经验公式(3)的回归系数5)。图8 日本初至3 s P波到时和c与震级的经验关系Fig. 8 Empirical relationships of c vs magnitude with initial 3 s P waves of Japan

注：图中的每一个点代表一条地震记录真实与估算震级的误差1)。虚线代表±标准差2)。σ和μ分别为震级误差的标准差值和均值3)。

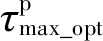
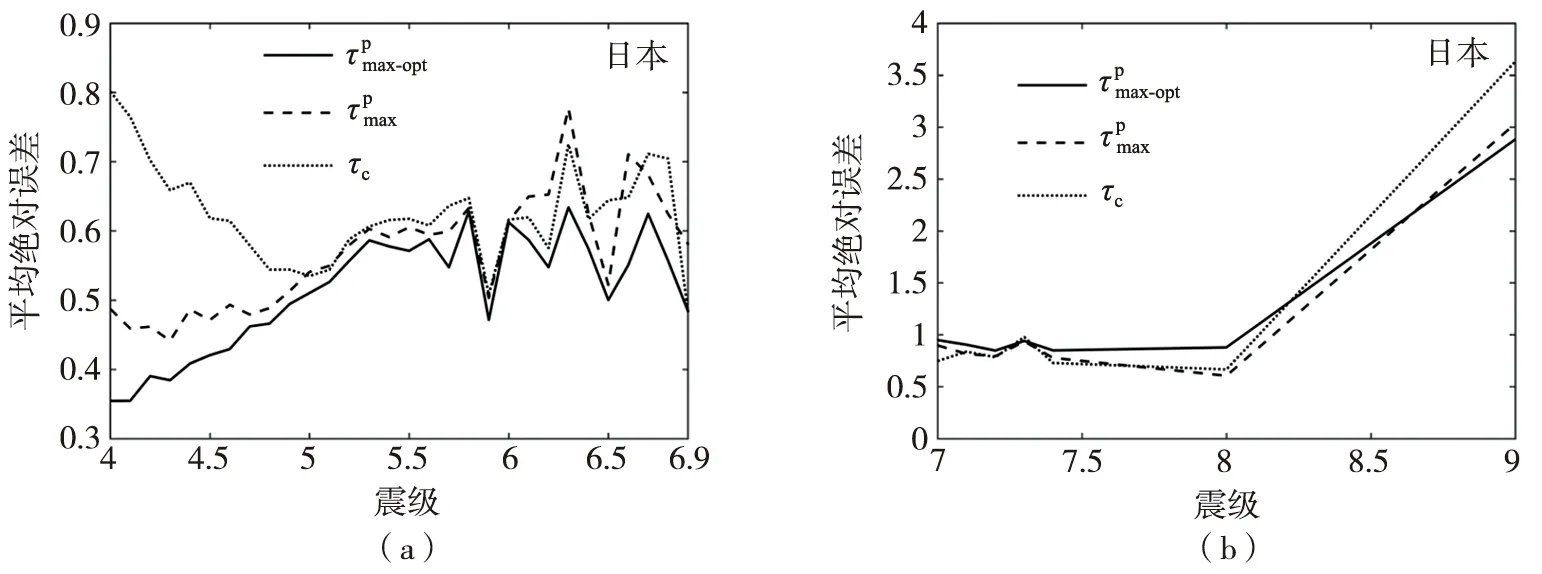
图10 日本初至3 s P波到时和c估算震级的平均绝对误差Fig. 10 Average absolute errors of magnitude estimated by and c with initial to 3 P waves of Japan

4.2 震级的持续估算

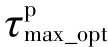
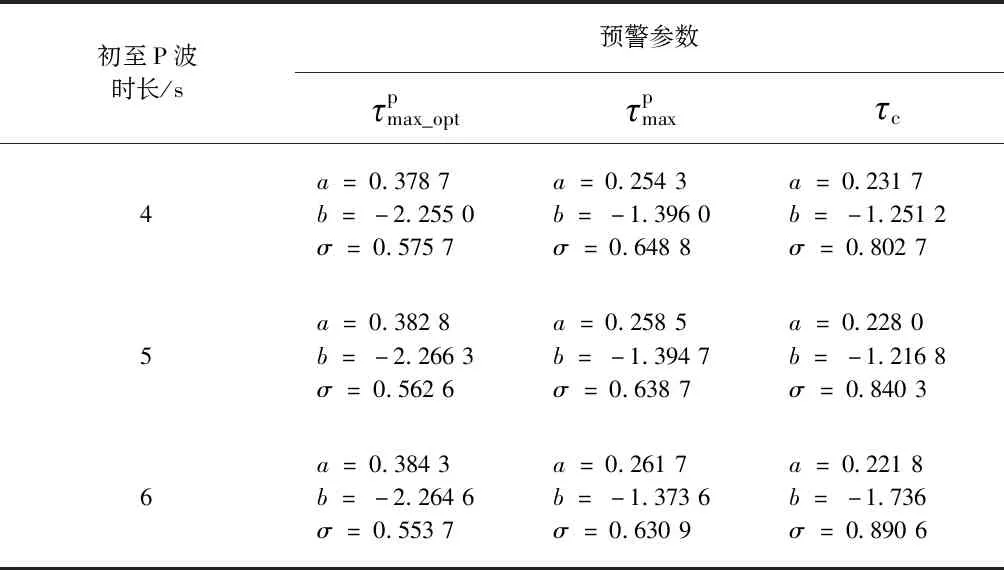
表1 日本初至4～6 s P波时经验公式的回归系数Table 1 Regression coefficients of empirical formulas with initial 4～6 s P waves of Japan

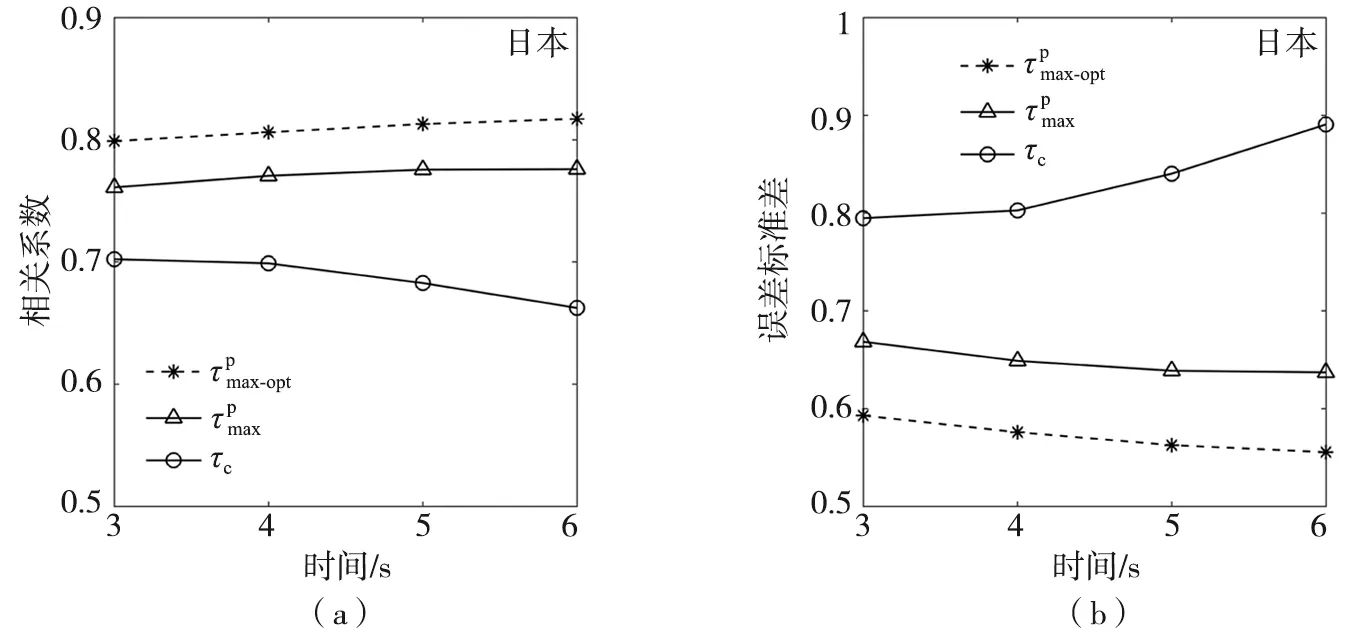
图11 日本初至3～6 s P波到时和c与震级的相关系数(a)和估算震级的误差标准差(b)Fig. 11 Correlation coefficients of and c vs magnitude (a) and standard deviation of estimated magnitude error (b) with initial 3～6 s P waves of Japan.

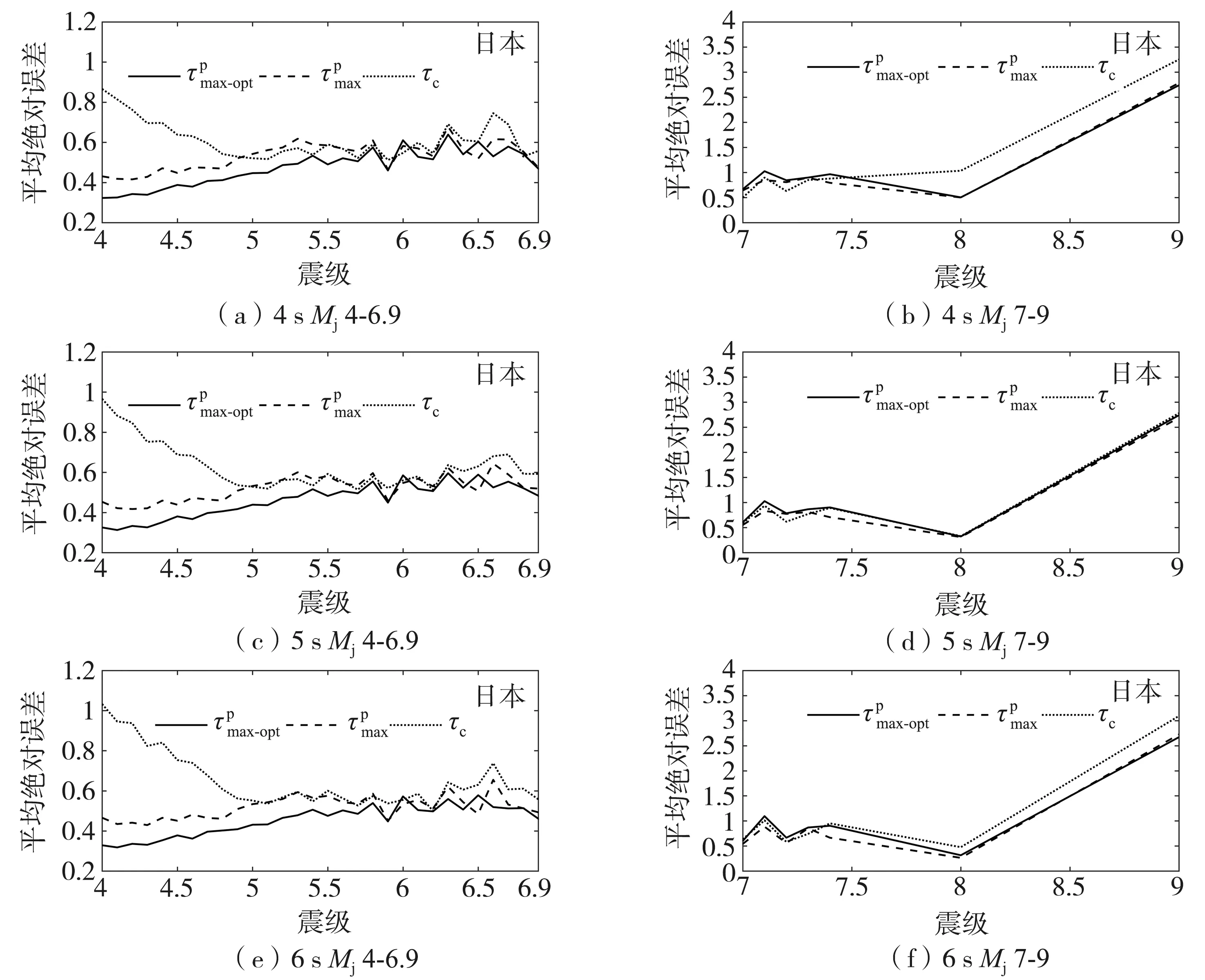
图12 日本初至4～6 s P波到时和c估算震级的平均绝对误差Fig. 12 Average absolute errors of magnitude estimated by and c with initial 4～6 s P waves of Japan

5 基于智利强震动记录的适用性测试

表2 智利初至3～6 s P波时经验公式的回归系数Table 2 Regression coefficients of empirical formulas with initial 3～6 s P waves of Chile

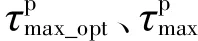
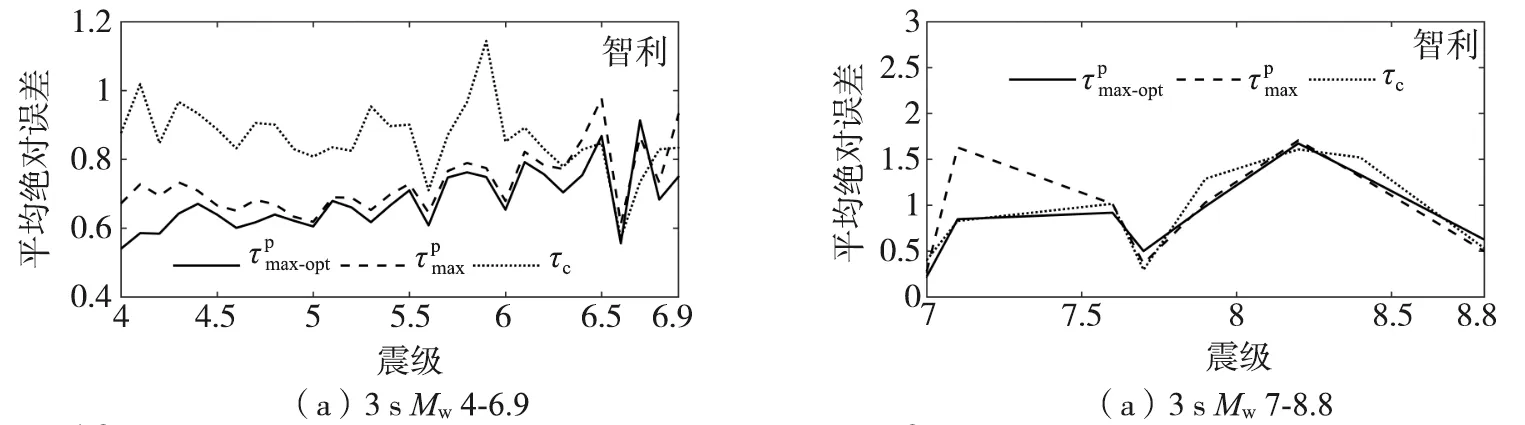
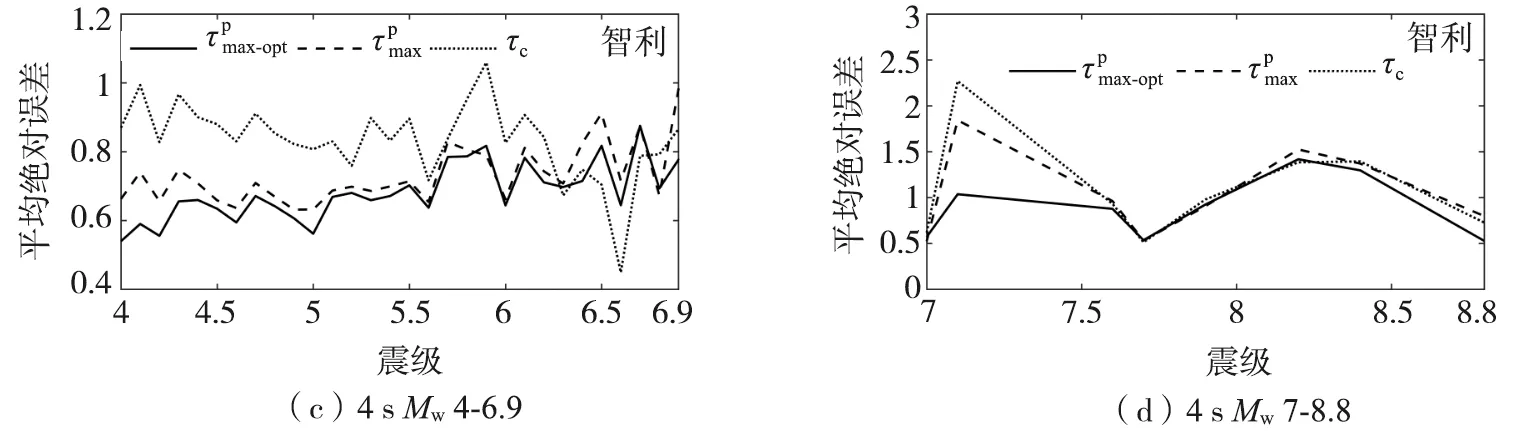
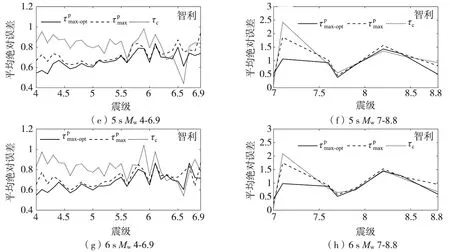
图14 智利初至3～6 s P波到时和c估算震级的平均绝对误差Fig. 14 Average absolute errors of magnitude estimated by and cwith initial 3～6 s P waves of Chile

6 结论

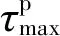
致谢：匿名审稿专家为本文提出了诸多宝贵的意见,在此衷心感谢!感谢日本防灾科学技术研究所(NIED,https：∥www.doi.org/10.17598/NIED.0004)和智利SIBER-RISK提供了强震数据下载服务。