山东临沂地区砂土剪切波速与标准贯入击数关系统计分析

岳庆霞,于一浦,杨 彬,王华林

(1.山东建筑大学 土木工程学院,济南 250101;2.山东省地震局,济南 250014)

0 引言

剪切波速(VS)是震动横波在土内的传播速度[1],是反映土体在地震作用下动力反应的一个重要物理量,是计算地基刚度和阻尼比的重要参数。在判定砂土地基液化、计算建筑场地地震卓越周期、对场地进行地震动小区划和地震反应谱分析时均需要钻孔进行剪切波速测试[2-4],在工程中有着广泛的应用。标贯击数(N)反映土层的密实程度,是土层密实程度划分的重要参数[5-6]。剪切波速与标贯击数同为反映土层密实程度的参数,二者之间存在一定的相关关系。《工程地质手册》中给出了砂土剪切波速和标贯击数的关系[7],然而在实际的工程场地中,受到各种不确定因素(环境噪音、土性和地下水埋深)的影响[8-9],整体来看很难用一个统一的标准去量化不同地区其内在的关系。因此有针对性地对某一地区进行两者之间的统计分析是有必要的。

李兆焱等[10]对唐山和巴楚地区液化土动力性能的研究比较中,采用了幂函数模型对砂土的剪切波速以及标贯击数进行了回归分析,指出二者虽有较强的相关关系但两地区的砂土体现出各自的区域特性;刘福兴等[11]从黄河三角洲的钻孔实测数据中得出相对于线性关系,指数统计回归模型更符合剪切波速与标贯击数的散点分布规律;刘颖[12]利用剪切波速与标贯击数的相关性确定了以剪切波速为判别依据的液化判别式;李存志等[13]从实测钻孔数据中考虑埋深与密实度得到昆明地区剪切波速与标贯击数的关系;袁晓铭等[14]在对哈尔滨地区砂土层的研究中指出,标贯击数或者埋深相同的情况下土层的剪切波速仍有较大差异,与地域的分布有着较为密切的关系;邱志刚等[15]将黑龙江地区的砂土进行分类,分别给出各自剪切波速与标贯击数的回归关系并取得了较好的拟合效果;郑灿堂等[16]给出了山东部分地区淤泥以及砂土等的波速与标贯击数的回归方程。但砂土包含多种砂,且随着土层深度的增加,砂土的粒径逐渐增大,从而影响剪切波速与标贯之间的关系;陈卫兵[17]利用黄河冲积平原地区多个火电厂的实测数据建立了土层标贯击数和剪切波速值的经验公式。从上述研究的各个模型来看：模型受地区影响比较显著。此外受砂土层粒径影响样本点集中区段分布不同,单一对标贯区段进行全域的回归分析误差较大。

临沂作为地震高烈度区,新构造运动活跃,但截至目前针对于临沂地区砂土的专项研究较少。近年来山东省启动“临沂市国际生态城地震断层探测与地震危险性评价”项目,获取了大量的探测数据,为研究临沂地区的场地特性提供了资料。本文首先对临沂地区不同砂土的剪切波速及标贯击数进行了回归分析,发现受沉积环境的影响,砂土层粒径与埋深呈正相关,砂土粒径越大其密实段样本点越多。为消除不同密实程度段之间的相互影响,对各类砂土进一步按照密实度进行划分,建立临沂以及周边相似地质条件的砂土N-Vs关系,并与实测数据进行了对比。

1 工程地质条件

1.1 临沂地区地理位置

临沂市位于山东省东南部,靠近黄海,东连日照,西接枣庄、济宁和泰安,北邻潍坊和淄博,南邻江苏,地跨北纬34°22′～36°13′,东经117°24′～119°11′。东西最大宽度161 km,南北最大跨度228 km,是山东省面积最大的地级市,如图1所示[18]。

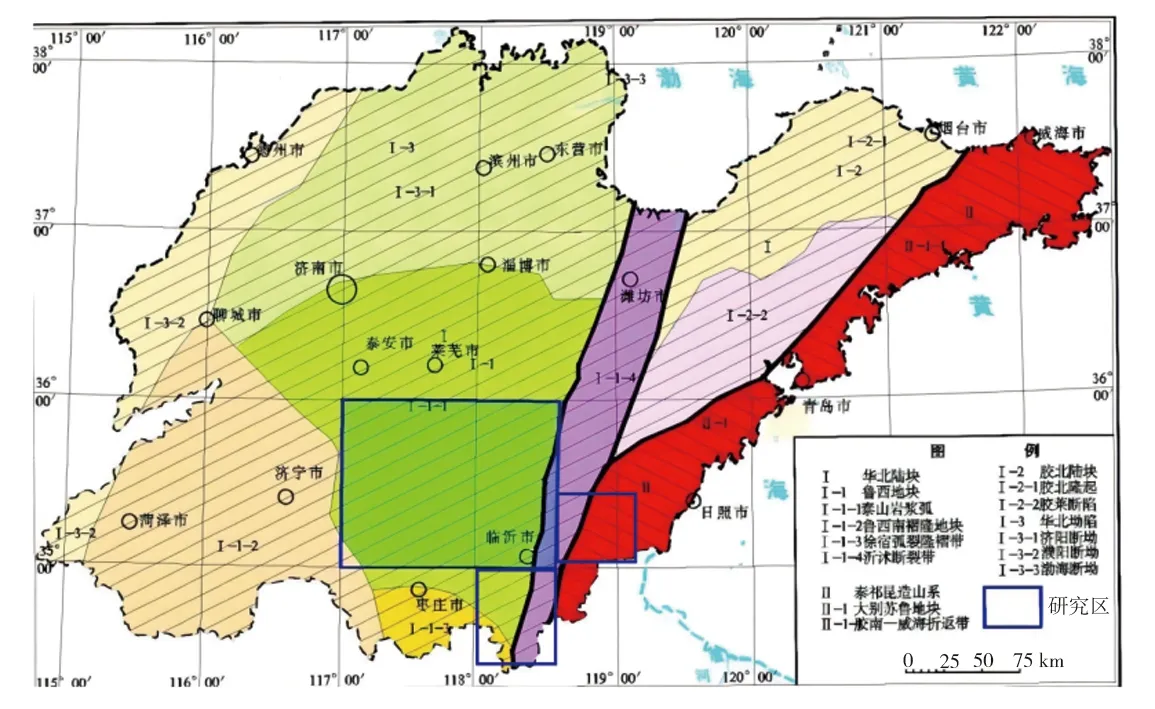
图1 临沂大地构造位置图Fig. 1 Linyi tectonic location map

1.2 地形地貌及区域地质构造

该区受北北东向沂沭断裂带西地堑沂水-汤头断裂和鄌郚-葛沟断裂地质构造控制,河流主要呈北北东向分布[19-20]。结晶基底为太古界泰山群地层,泰山群为一套中深变质的结晶片岩和混合岩。自早寒武世晚期到中奥陶世沉积了一套海相或海陆交互相碳酸盐岩和砂页岩为主的沉积物。中奥陶世末,加里东运动上升为陆地,长期遭受剥蚀,缺失了下奥陶统、泥盆系、志留系和下石炭统地层,仅在鄌郚-葛沟断裂西侧狭长地带发育中石炭统本溪组砂砾岩和粘土岩含铁矿地层沉积[21-23]。这些基岩地层构成了该区第四系沉积物的主要来源(图2)。该区位于沂河和祊河流经区,为河流冲洪积区,此研究土体深度在2～15 m,主要为第四系冲洪积砂土层。

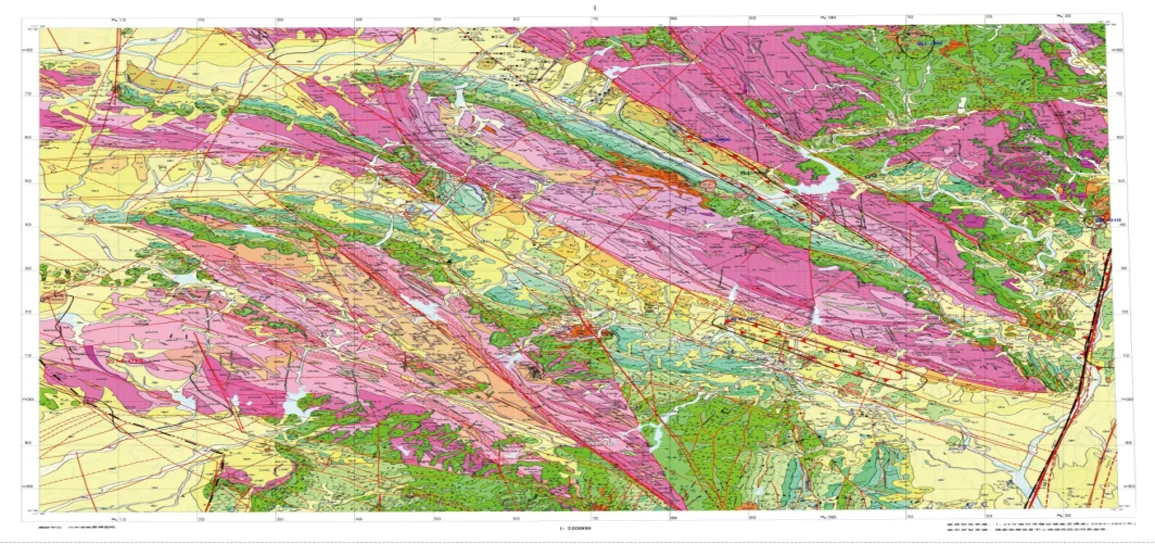
图2 1∶250000临沂市建造构造图(公开版)Fig. 2 1∶250000 Linyi city construction structure (public version)

2 原始资料的采集与选取

本文用于研究的资料来源于山东省地震工程研究院2014年对临沂各个县区的安评报告及县区的地震小区划报告。剪切波速测试工作采用单孔法,采用的仪器具有分时采样、叠加、滤波和信号增强等功能,保证了测试结果的真实可靠。在资料的选取过程中剔除掉了一些影响分析结构的资料[4,9,24](例如工程场地相近导致钻孔位置相距较近或由测量误差导致的“坏点”)。最终筛选出了大约50个工程场地(207个钻孔)的安评资料以及地震小区划报告。所选工程场地基本涵盖临沂各个县区,样本资料主要包括砾砂等各种砂土。表1列举了统计样本的详细信息,包括钻孔数、标贯击数和剪切波速范围等。

表1 原始资料的采集与选取Table 1 Collection and selection of original data

续表

3 临沂地区砂土剪切波速与标贯击数的数据拟合分析

3.1 总体数据拟合分析

众多学者[14,17,25]研究表明：标贯击数N与剪切波速VS之间的关系可以幂函数的形式来表示。即

VS=aNb

(1)

式中：a和b分别是回归的参数。采用上述方程对剪切波速和标贯击数进行回归分析,得到了砾砂、粗砂、中砂和细砂四种砂土剪切波速VS和标准贯入击数N的回归分析关系。回归曲线及预测均值±标准差曲线如图3-6所示,其拟合公式及相关参数见表2。

表2 砾砂、细砂、中砂和粗砂的回归参数Table 2 Regression parameters of gravel sand,fine sand,medium sand and coarse sand

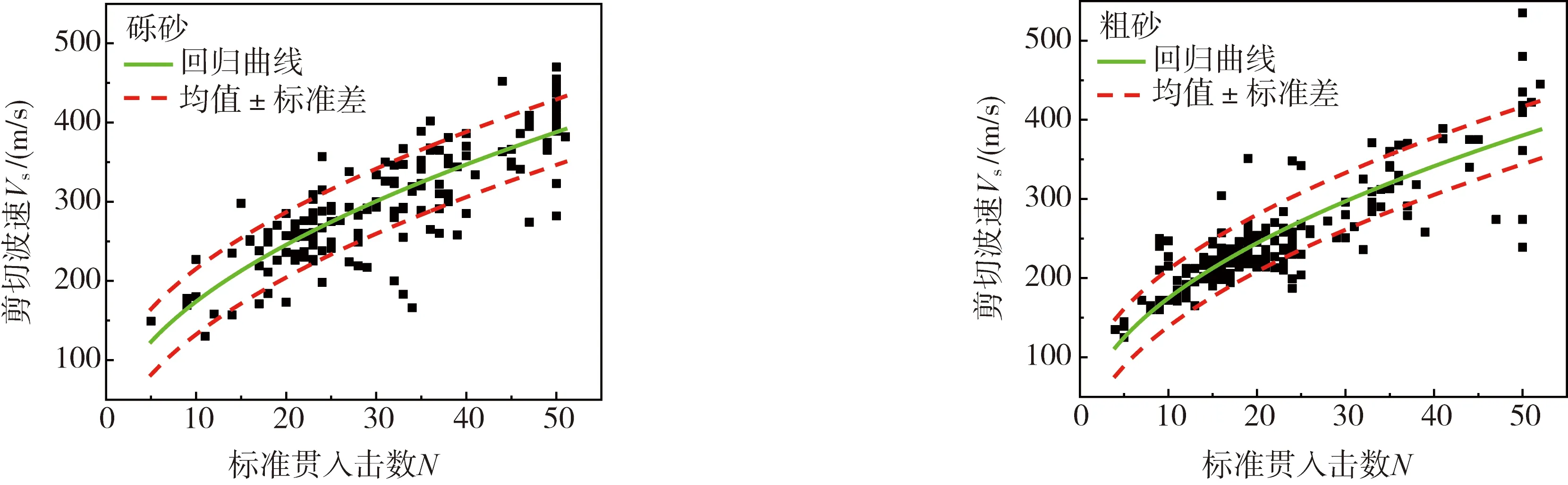
图3 砾砂剪切波速与标贯击数的统计分析 图4 粗砂剪切波速与标贯击数的统计分析Fig. 3 Statistical analysis of shear wave velocity and standard penetration test blow count of grave sand Fig. 4 Statistical analysis of shear wave velocity and standard penetration test blow count of coarse sand

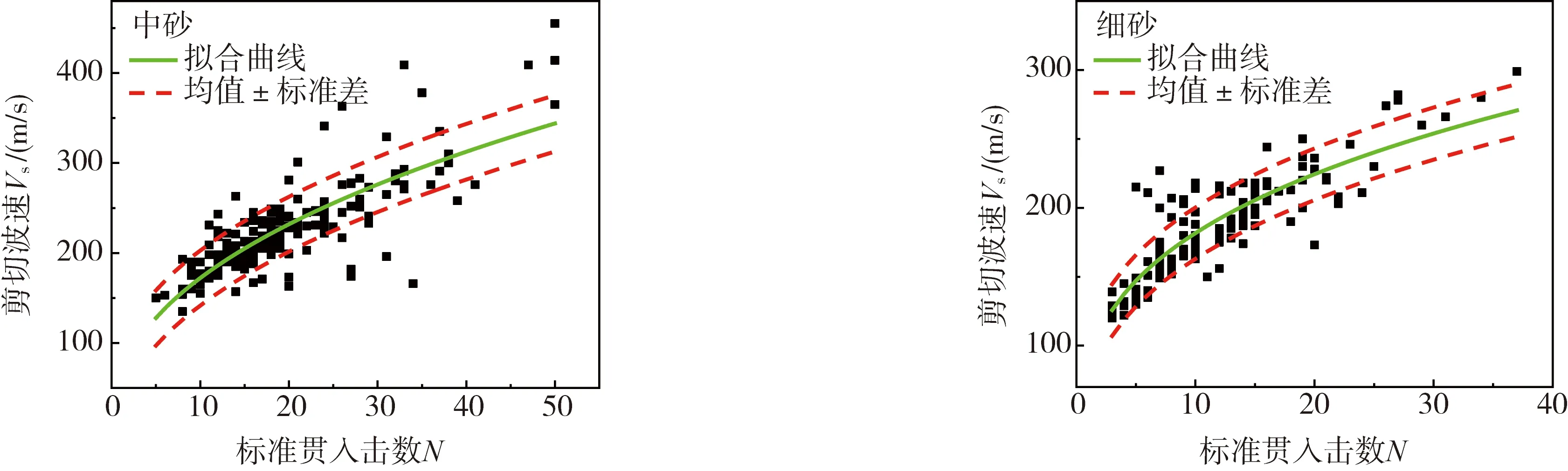
图5 中砂剪切波速与标贯击数的统计分析 图6 细砂剪切波速与标贯击数的统计分析Fig. 5 Statistical analysis of shear wave velocity and standard penetration test blow count of medium sand Fig. 6 Statistical analysis of shear wave velocity and standard penetration test blow count of fine sand

从图3-6来看：砾砂的整体离散性最大,这与砾砂粒径有较大关系,其次受沉积环境和测量误差影响,对于埋深较小的砾砂层土层性质的不稳定也是导致其离散性大的主要原因。从拟合曲线上看砾砂在标贯击数大于20区段拟合较好;粗砂和中砂则在标贯击数20左右区段拟合较好;细砂在标贯击数小于10区段拟合较好。而对于其他标贯击数区段的拟合效果较差,以细砂为例在标贯击数大于25区段,拟合的回归曲线明显偏离样本点。从上述现象可以看出：由于不同种类砂土粒径含量影响标贯击数,砂土粒径大的区段的标贯击数也有所增大。一般来说,砂土的粒径越大,埋深越大。但山东临沂地区受地壳运动影响,部分粒径较大的砂土层也处于埋深较浅的位置。从所获得的样本点来看：每一种砂土在每一个密实度区间的样本点数量是不一样的,且砂土粒径越大其标贯击数大的样本点越多,故在进行回归分析时,回归方程容易受某一密实区段的影响,故需要先对砂土进行密实度分区再进行回归分析。

3.2 基于密实度的分段拟合

因安评报告中砂土层密度数据不完整,故对砂土以标贯击数为依据进行密实度区分,然后再进行分区段拟合(图7-10),其结果列于表3-表6。根据标贯击数将各类砂土分为松散、稍密、中密和密实四个区段[1](松散N≤10、稍密1030),分别进行剪切波速VS和标准贯入击数N的回归分析。

图9 中砂分段剪切波速与标贯击数的统计分析 图10 细砂分段剪切波速与标贯击数的统计分析Fig. 9 Statistical analysis of sectional shear wave velocity and standard penetration test blow count of medium sand Fig. 10 Statistical analysis of sectional shear wave velocity and standard penetration test blow count of fine sand

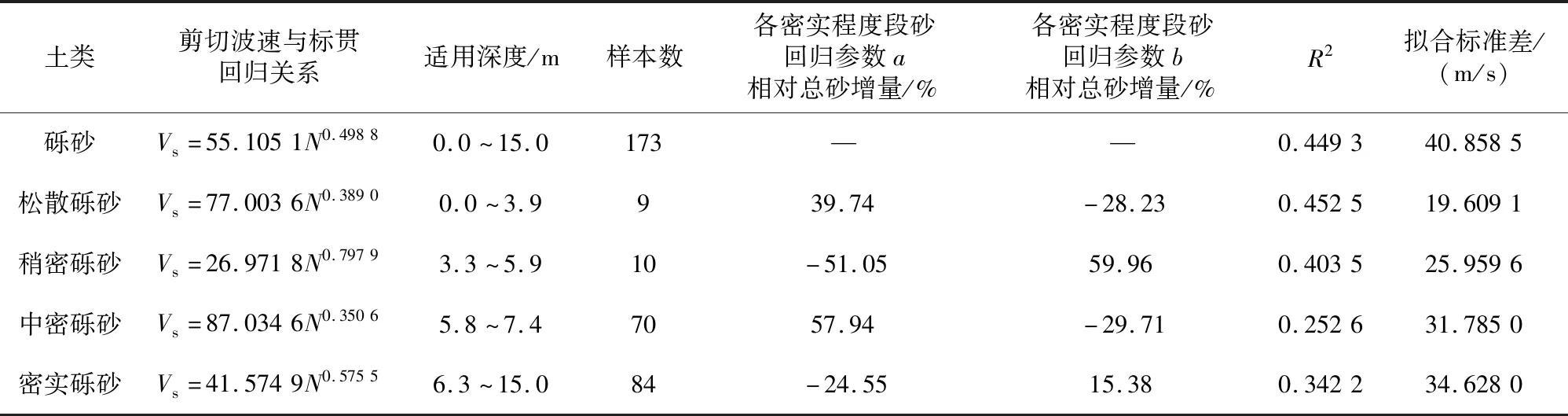
表3 砾砂区分密实度回归参数比较Table 3 Comparison of density regression parameters for gravel sand differentiation

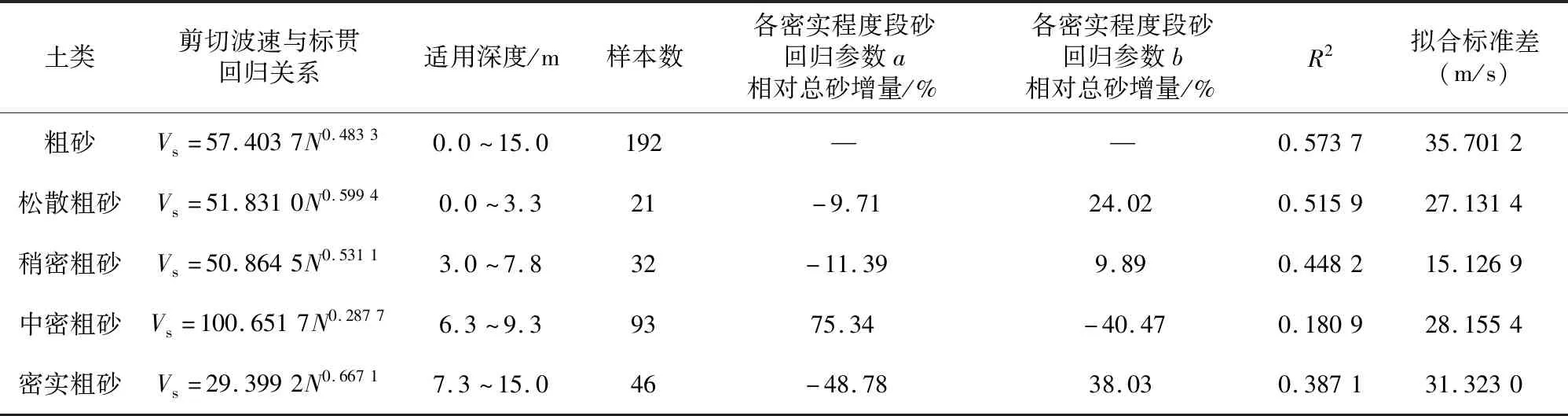
表4 粗砂区分密实度回归参数比较Table 4 Comparison of density regression parameters for coarse sand differentiation

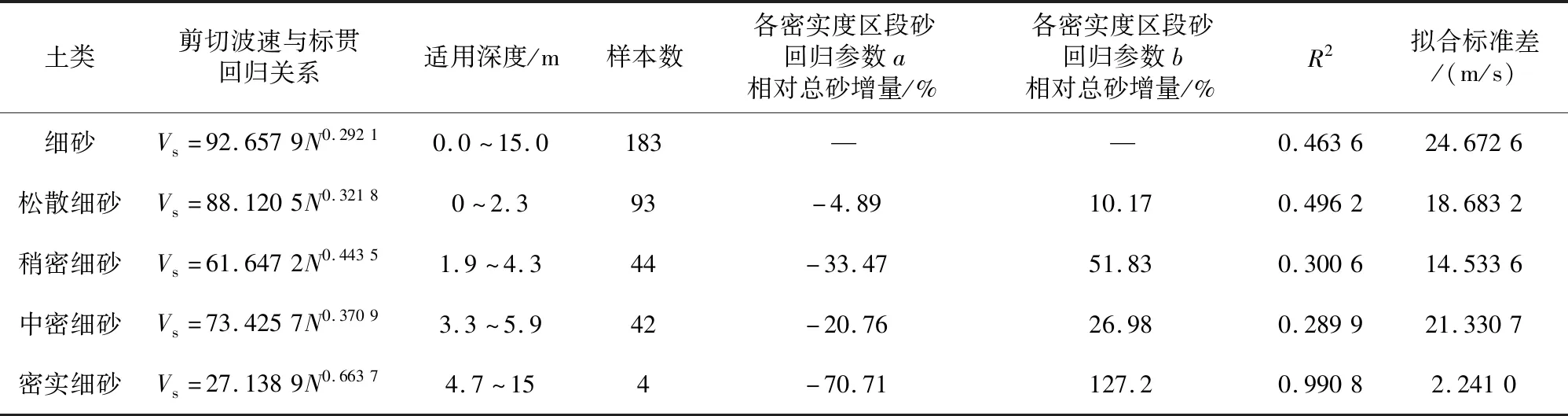
表6 细砂区分密实度回归参数比较Table 6 Comparison of density regression parameters for fine sand differentiation

从表3-表6中可以看出：针对不同密实度砂土的回归参数相比于整体的拟合有较大差异,尤其在数据量少的区段差异较大。各密实度砂回归参数a相对总砂增量最大为87.87%,最小为-78.08%;各密实度砂回归参数b相对总砂增量最大为127.2%,最小为-55.27%。分段拟合的标准差均小于全域拟合,说明相较于全域拟合,分段拟合精度更高。此外,分段拟合的R2大部分小于全域拟合,原因是存在样本最大(小)值对样本容量小的分段拟合的影响显著,导致出现分段拟合的R2大部分小于全域拟合的情况。从图7中看出砾砂中全域拟合和分段拟合差别主要出现在松散和稍密区域,由于有相对较多的样本点趋向于标贯击数大的区段,导致对松散、稍密区域拟合效果较差,且砾砂粒径较大,对于埋深较浅标贯击数小的砾砂层在沉积过程中容易受上下土层的影响。实际砂土层剪切波速受杂质的影响,故在对砂土层剪切波速进行预估时,可以综合前人有关剪切波速和土层埋深的研究[4],对预估结果进行考量;图8-9中看出粗砂、中砂全域拟合和分段拟合差别较大的出现在松散以及密实区段,稍密和中密区段样本点多是误差出现的主要原因;从图10中看出细砂的全域拟合和分段拟合中差别最大的出现在中密、密实区域,这是因为细砂的样本点中稍密以下的占据较多比重,高标贯击数段受到其他土层的影响的模拟中存在较大误差。除此之外,密实细砂的样本太少也是导致统计参数变化幅度大的原因。因此建议在对密实细砂剪切波速的预测过程中应综合考虑埋深等因素并补充一定数量的样本。

总之,两种统计分析方法区别在于对除标贯击数集中的其他区段的模拟,研究区地处第四系冲洪积砂土层,新构造运动活跃,标贯击数集中区段与砂土层粒径正相关,出现局部数据较为集中的现象。

3.3 基于实际数据的模型验证

为佐证分段模拟的适用性,本文选取了场地地震安全性评价中部分钻孔,给出了两种回归统计方法得到的剪切波速与实际测得的波速对比。三个钻孔中分段模拟所得的剪切波速误差小于全域模拟所得,其中⑦⑧⑩样本效果明显,误差分别减少11.7%、13.0%和12.5%,结果列于表7。

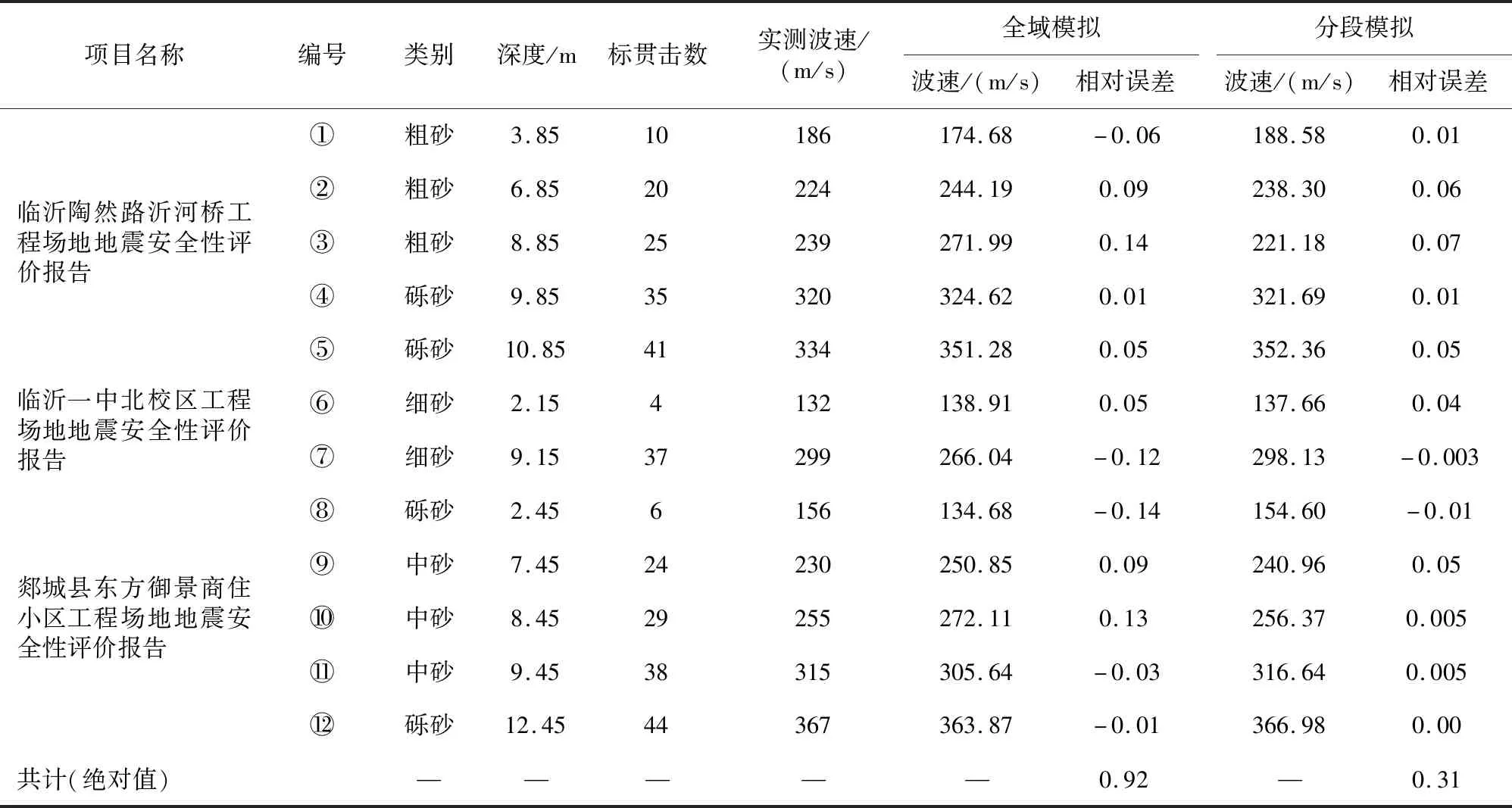
表7 全域模拟与分段模拟在实际工程中的对比Table 7 Comparison of global simulation and segmented simulation in actual engineering

3.4 与国内其他地区对比分析

国内其他地区的N-Vs关系多以砂土为整体进行研究分析[5,11,13-14],未按照密实度对砂土进行分类。为便于对比分析,临沂地区砂类土的N-Vs关系取四种砂土在各标贯区段的平均值。图11为不同地区砂类土剪切波速与标贯击数回归方程的对比曲线。

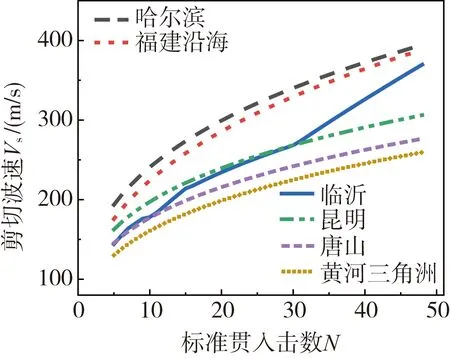
图11 国内各地区砂土N-VS关系曲线对比Fig. 11 Comparison of N-VS relationship curves of sandy soil in various regions of China

从图中看出国内各地区砂类土剪切波速与标贯击数均呈正相关变化,但在具体数值关系上存在显著差异。表现为同一标贯击数下临沂地区砂土层剪切波速明显小于哈尔滨地区,大于黄河三角洲地区;在同一剪切波速下哈尔滨地区砂土层标贯击数最低,临沂地区居中,黄河三角洲地区最大。这也进一步说明不同地区进行数据统计拟合分析的必要性。

在标贯击数大于30区段临沂地区的N-Vs曲线斜率明显大于其他地区。这与统计方法有较大关系,原因是其他地区在确定N-Vs关系时采用全域模拟且不区分砂土类型,样本点的标贯击数集中在5～30区段,故该区段临沂的分区段模拟与其他地区N-Vs曲线切线斜率变化基本相同;高标贯击数区段样本点偏少甚至缺失N-Vs曲线受样本点集中区段影响[13],全域模拟所得剪切波速变化率偏小。这也进一步说明临沂地区分段模拟的必要性。

4 结论

本文通过两种方法对临沂地区207个钻孔,760组砂土样本进行了剪切波速和标贯击数的的统计回归分析,并与我国各地区的N-Vs关系进行了对比,得出以下结论。

1)临沂地区砂类土剪切波速与标贯击数的统计分析符合幂函数关系。该研究区主要为第四系冲洪积砂土层,受沉积环境影响在机械沉积分异作用下标贯击数集中区段与砂土层粒径正相关,致使回归方程易受某一标贯集中区段的影响,存在对整体的模拟不够精确的弊端。

2)以标准贯入击数为依据将各类砂土进行密实程度划分,再针对每一区段进行回归分析的分区段模拟能更好表征砂土的N-VS关系。

3)将两种方法带入到实际工程中的12组砂土样本进行验证,发现相比于全域模拟,以密实度为划分标准的分区段模拟误差最大减小13%,平均减小5.08%。

4)较于全域的统计分析,以标准贯入击数为划分标准的分区段模拟能有效减小N-VS关系误差。本文研究数据建立在实测基础上,对于临沂及周边地区地震勘察试验工作具有工程应用价值。

5)临沂地区的N-Vs关系与其他地区相比存在差异性,在实际地质工程勘测中若需估算剪切波速,应选用本地区回归方程。