基于卷积神经网络的地震波形智能识别研究

郑 周,林彬华,金 星,韦永祥,丁炳火,陈 辉

(1.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080;2.地震灾害防治应急管理部重点实验室,黑龙江 哈尔滨 150080;3.福建省地震局,福州 350003)

0 引言

目前地震波形的分类和判别仍然是地震学领域的一个热点问题,随着布设的台站越来越多、越来越广,台站仪器精度不断提高,观测到地震波形的数量和种类也越来越多[1-2]。地震台站收集到的波形为地震、背景噪声、爆破、机械振动、干扰或异常波形,若不将这些波形进行分类,很可能会给地震预警带来误触发,也会给日常地震监测带来误导性结果,故地震波形分类对地震学研究和地震预警应用具有重要的意义。目前这一分类工作大多通过人工来完成的,不仅费时,还考验分析人员的专业水平,难免会出现一些错误[1]。为了解决这一问题,地震学家们发展了许多种类的自动识别算法,如下几种是比较典型的几类：基于振幅的长短时平均算法(STA/LTA)和基于Akaike信息准则的方法(AIC)等方法[2]。这些方法各有长处和短处,如长短时平均算法(STA/LTA)对于信噪比高的信号识别率比较高,对于信噪比低的信号则不是很敏感,因此往往会漏掉。AIC方法与STA/LTA相比较则能更准确估计地震信号的到来,但同样也依赖信噪比的质量。以上几种传统检测方法虽然能够快速检测触发信号,但是无法甄别地震、干扰或异常波形。

随着计算机技术的高速发展,机器学习被广泛的运用在图像识别、信号处理、手写识别、评估、预测、组合优化和知识工程等领域[3-4]。近年来地震学家们在地震学的研究中也引入了深度学习的方法,例如赵明等[5]应用卷积神经网络对汶川地震余震波形和首都圈进行自动分类与识别,其训练和检测准确率均达到95%以上。ZHANG等[6]应用卷积神经网络实现了微震波形分类,结合小波变换将频谱分解为时频谱,区分地震信号和干扰噪声;MEN-ANDRIN等[7]使用了几种神经网络模型对实时的地震信号和噪声进行了判别,能迅速的识别地震和干扰信号,准确率高达90%以上;LI等[8]结合了生成对抗神经网络和随机森林对南加州和日本约70万地震和噪声波形进行了训练,该模型可以识别99.2%的地震P波和98.4%的噪声信号;CHEN等[9]结合K平均算法和卷积神经网络对地震波形进行分类,通过对不同噪声水平的合成微震资料和野外微震资料的应用分析,发现K-CNN模型能精确地将地震波形进行分类;ZHANG等[10]用经验模式分解EEMD和卷积神经网络对地震信号进行分类,分类的结果高达93.85%;宋晋东等[11-12]运用人工智能的方法对地震动峰值和震级进行了预测,其离线模拟测试结果优于传统方法;LINVILLE等[13]、ZHANG等[14]、LI等[15,17]和BRAS等[16]运用深度学习的方法对地震事件进行了判别,准确率均在90%以上。以上这些人的研究进一步证明了深度学习在地震学上存在一定的发展潜力。但他们对异常波形的判别还没有得到很好的解决,为此本文设计了一种基于卷积神经网络对异常波形自动识别的方法,以三通道波形作为卷积神经网络的输入,地震、噪声、爆破和异常作为输出,训练出3 s样本波形的预测模型。相比于传统神经网络单一的提取特征,该方法更加全面、更加可靠和稳定,能更加准确的对地震、噪声、爆破、异常波形进行分类与判别,证明了该模型能够在地震监测预警中快速和精确地对波形进行分类。

1 数据与方法

福建省测震台网由88个测震台站、16个台湾省台站及12个周边邻省台站共116台组成[18-19]。本文收集并处理了2012—2017年福建测震台网记录到的683个地震事件(ML>1,震中距<100 km)和478个爆破事件作为研究数据如图1所示。这些事件波形均由福建省地震局专业的地震分析人员做过地震编目分析,所记录到地震事件和爆破事件均包含E、N和Z三分量波形,台站观测数据的采样率均为100 Hz,全部都为扣除台站仪器响应后所记录的实际地动速度(单位 um/s)[19]。

图1 本研究中所使用的数据集信息Fig. 1 Information of the data set used in this study

1.1 训练样本预处理

研究样本是根据地震事件的P波到时信息所截取的：截取P波到时和P波到时后3 s共3 s作为模型所训练的地震波形样本;截取P波到时前5 s和P波前2 s共3 s作为模型所训练的噪声波形样本[19],同样对爆破和异常波形的截取长度也是3 s,将标定、方波、突跳和仪器故障波形都视为异常。图2(a)～图2(d)分别是3 s地震、噪声、爆破及异常的波形样本图。

图2 本研究中使用的3s波形数据的例子Fig. 2 Examples of 3s waveform data used in this study

1.2 训练集和测试集

首先建立一个波形分类器作为监督学习的过程,监督式学习是需要一个包含先前知识的学习数据集来训练卷积神经网络分类器,学习所用的数据集是由输入特征和输出特征标签组成,输入的特征就是原始波形,输出的则是地震、噪声、爆破和异常[19]。将收集并处理好的2012—2016年福建省、台湾省及周边邻省测震台网所记录的数据作为训练集样本,为了保证训练样本的均匀性,截取的地震、噪声、爆破和异常波形的样本数量相同,获得了5 500条地震波形、5 500条噪声波形、5 500条爆破波形和5 500条异常波形,共22 000条波形样本作为训练集,收集并处理了2017年福建省、台湾省及周边邻省测震台网所记录的数据作为测试集数据,同样保证测试的公平性,截取并获得了1 375条地震波形、1 375条噪声波形、1 375条爆破波形、1 375条异常波形和共5 500条波形样本作为测试集。

1.3 样本标签生成

由于神经网络具有较强的分类能力,因此把地震、噪声、爆破和异常当作四分类问题处理[20]。地震作为第一类,输出的标签结果为0;噪声作为第二类,输出的标签结果为1;爆破作为第三类,输出的标签结果为2;异常作为第四类,输出的标签结果为3(见表1)。

2 卷积神经网络模型的搭建

针对地震波形分类识别问题上,采用单台三通道的3 s波形作为输入,地震、噪声、爆破和异常波形作为输出。卷积神经网络通过卷积核(滤波器)进行卷积操作,从而提取地震波形特征,若想提取更多的特征,则可以设置多层卷积层,但也要防止神经网络模型出现过拟合的情况,需要合理设置,结合以上流程,最后通过类似投票的形式输出对应的波形类型的概率如图3所示[19-23]。

表1 地震波形分类及标签Table1 Classificationandlabelingofseismicwaveforms标签波形分类0地震1噪声2爆破3异常图3 卷积神经网络的输入与输出流程图Fig.3 Inputandoutputflowchartofconvolutionalneuralnetwork

2.1 卷积神经网络的原理

卷积神经网络是一种前馈多层神经网络,用于处理多维数组,通过卷积、池化和全连接层组成的多个隐藏单元序列,将输入特征转换为输出类别概率。每一层卷积层中都包含一组线性或者非线性滤波器,用于提取前一层的局部特征,通过使用一个校正的线性单元将所有的负响应映射为零,SW-CNN选择的是RELU激活函数(如公式1),可以加快模型的训练速度：

(1)

式中：bj和wij分别代表卷积神经网络中第j个神经元的偏置和权重,该神经元通过将上一层的输入Xi传递到这一层的输出特征Xj。通常把相似的局部特征合并成一个特征,对生成的特征进行空间下采样(又称池化操作),池化操作可以在模型训练的过程中减少自由参数的数量,改善网络模型的性能,防止出现过拟合的情况。由一系列卷积层、非线性激活层和池化层产生的输出特征映射以串联的形式被传递到全连接层,每一个神经元都与上一层的所有激活连接,连接的方式都是线性的。最后一个全连接层的输出将会被输送到一个归一化指数函数(Softmax分类器),该函数的作用是计算N个不同可能类别的概率分布(如公式2)[19,21-23]：

(2)

式中：xj为最后一层输出x的第j个元素值,Pj为第j个元素所输出的概率值,通常所输出的概率值会在0～1之间,值越大说明可能性越高。本文所研究的目标是寻找一组可学习的自由参数,通过使用L2正则化多项逻辑损失函数(如公式3),最大限度的减少与真实值间的误差：

(3)

式中：正则化参数λ是控制数据失配和模型约束之间的权衡,并控制模型各层的参数(偏差和权重)。通过使用梯度下降法来寻找目标的最优解,该方法通过损失函数的负梯度和来自前一次迭代的模型更新的线性组合来计算每次迭代时来进行网络参数的更新(如公式4)：

ΔWt=μΔWt-1-α∇J(Wt)

(4)

式中：学习率α是负梯度的权重,动量μ控制模型中的每一次迭代参数的更新,对于比较大的训练集,可以在每次迭代中抽取训练集的小随机选择(小批量)来估计代价函数的随机近似将更有效。

2.2 网络模型的调参试验

构建一个完整的卷积神经网络模型需要设置适当的卷积层、池化层和全连接层的层数,以及选取适当的卷积核的大小、卷积步长、激活函数、训练批次等参数。SW-CNN模型是在Tensorflow2.0和Pycharm上搭建的,本文所用的硬件配置以及软件的使用见表2。

表2 模型的硬件和软件环境Table 2 Hardware and software environment of the model

参数的选择参考了前人选取的原则[3-4,19-28],对于输入的三通道地震波形进行了检测分析,采用的卷积核大小是3×3,卷积层的通道数是64,每一批次选取256个样本,最大迭代轮数选择的是10 000,每1层都引用了RELU激活函数。表3展示了SW-CNN模型的调参试验,用来对比模型结构的优良性。从表3中的T01、T02和T03这三个对比试验看出：T03的效果最好,T01的效果最差,可得6层卷积结构较优;从表3中的T03、T04和T05这三个对比试验看出：T04的效果最好,可得2层全连接层结构较优。综上所述,选取6层卷积和2层全连接层的网络模型结构的试验效果最优。另外,本文是在CPU配置的工作站上进行训练的,调参耗时会比GPU配置上的工作站慢很多,对于耗时问题,今后会进行改善。

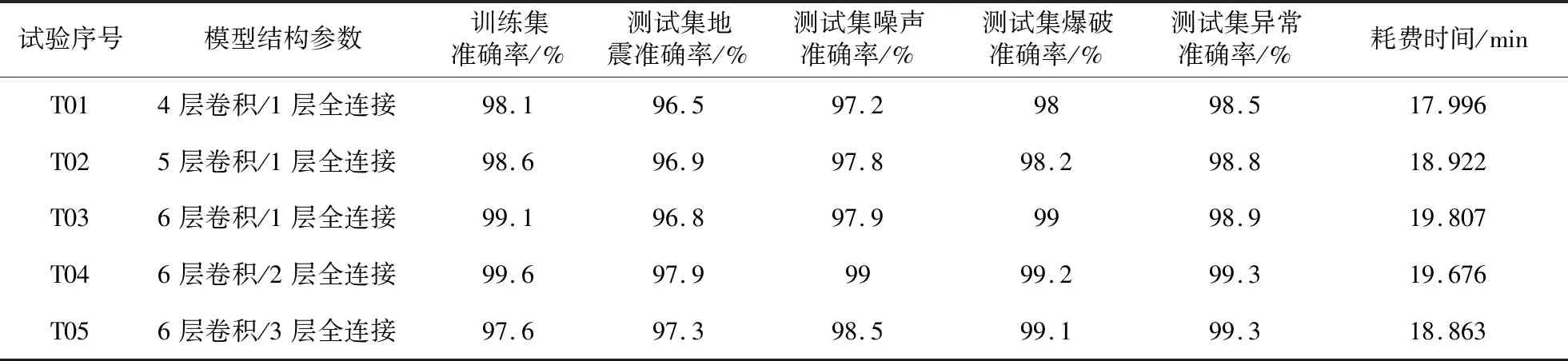
表3 模型的调参试验Table 3 Parameter adjustment experiment of the model

2.3 卷积神经网络的模型架构

与传统的神经网络不同,卷积神经网络是由不同类型的隐藏层组成的,如图4所示。以长为3 s的地震三通道波形作为输入数据,并对输入数据进行3×3卷积操作,在卷积操作若出现空白的部分,则用0来做填充处理,然后便进行2×2的池化操作。第1～6层都进行了卷积和池化操作,输入的特征图从原来是64@300变为了64@10,最后通过Flattenning将其变为一维向量,展开共得到了640个特征点,通过全连接层和Softmax函数将其用概率分布的形式输出成地震、噪声、爆破和异常。SW-CNN模型采用了ADAM优化算法、运用了L2正则化操作、学习率为0.001、网络的训练迭代次数为10 000和训练的目标损失误差为0.06。

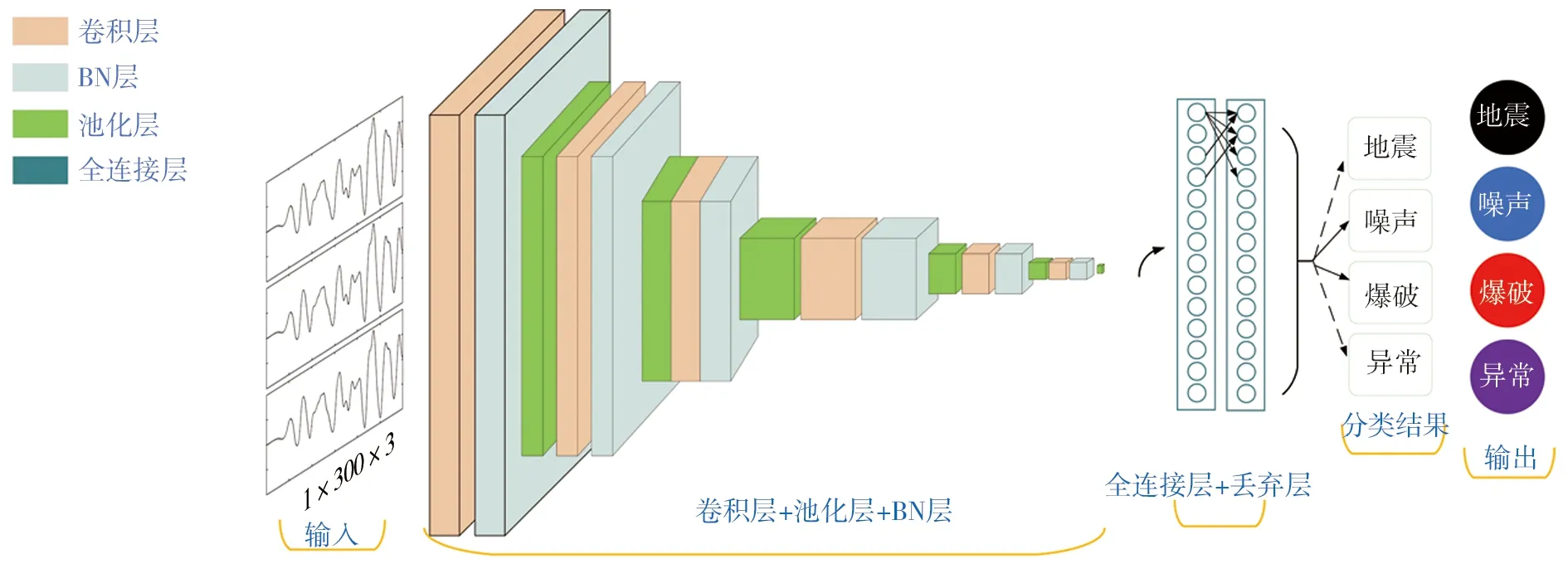
图4 卷积神经网络模型架构Fig. 4 Convolutional neural network model architecture

3 结果分析

3.1 评价指标

用Precision(准确率)、Recall(召回率)和F1-score(F1分数)对地震波形分类的卷积神经网络模型进行评价[24-27]。其中准确率被定义为模型正确预测出为正的样本的数量,召回率被定义为有多少正例的样本被预测出来的数量,F1分数则是对准确率和召回率的一种调和平均。计算准确率、召回率和F1分数的公式(5)—公式(7)：

Precision=TP/(TP+FP)

(5)

Recall=TP/(TP+FN)

(6)

F1=2×Precision×Recall/(Precision+Recall)

(7)

式中：TP代表的意思是真阳性,FP代表的意思是假阳性,FN代表的意思是假阴性。在完美的卷积神经网络中：TP的值为1,FP的值为0[7]。

3.2 SW-CNN模型分类结果分析

利用训练集中收集并处理的22 000条三通道波形样本,训练出SW-CNN模型,并用测试集中收集并处理的5 500条三通道波形样本对SW-CNN进行测试,用来验证SW-CNN模型的优良性,由于样本量充足,因此测试集并没有采用数据增强策略(如滤波和去噪等操作)。本文以正确分类到不同波形类别的百分比来评估卷积神经网络模型的鲁棒性,从表4可得：测试集对地震的识别准确率为97.9%,对噪声的识别准确率为99%,对爆破的识别准确率为99.2%,对异常的识别准确率为99.3%,得出SW-CNN模型能有效地对地震、噪声、爆破和异常波形进行分类。

如图5混淆矩阵所示(每一行之和表示该类别的真实样本数量,每一列之和表示被预测为该样本)[6,15],地震波形出现了29次分类错误,噪声波形出现了14次分类错误,爆破波形出现了11次分类错误,异常波形出现了10次分类错误。可以看出SW-CNN模型对异常波形的识别率优于另外三种波形,且对另外三种波形的识别率均超过97%,有利于进一步更深层次的研究。

表4 评估方法的精度结果 Table4 Accuracyresultsofevaluationmethods %波形类别PrecisionRecallF1地震97.99997.6噪声9997.898.4爆破99.29999.1异常99.399.499.3图5 地震波形分类的混淆矩阵Fig.5 Confusionmatrixofseismicwaveformclassification

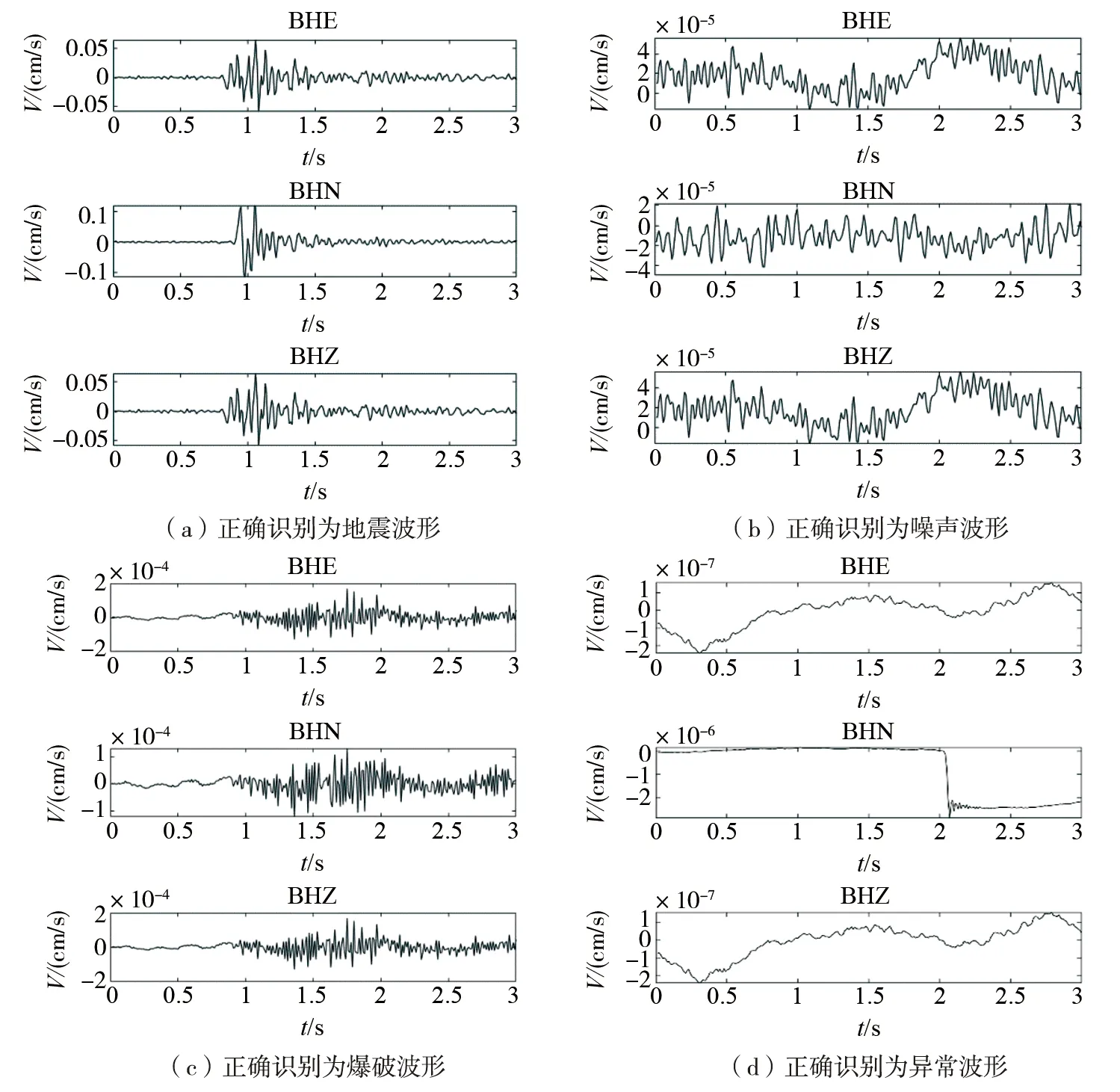
测试集正确分类的波形样本如图6(a)-图6(d)所示,测试集错误分类的波形样本如图6(e)-图6(f)所示,测试集检测出人工误标识为波形样本如图6(g)-图6(h)所示。图6(e)模型将噪声波形误判别成了地震波形,图6(f)模型将爆破波形误判别成地震波形,可能是震级较小的地震或震中距较远的台站地震记录相比于爆破更容易被噪声淹没,导致地震被误判别成爆破。从图6(g)可以看出这是一张地震波形图片,但在准备数据集时把它错误标成了噪声,但是模型正确把它也判定成了地震波形;从图6(h)可以看出这是一张噪声波形图片,在准备数据集时把其错误标成了地震,但是模型正确把它判定成了噪声波形。把图6(g)-图6(h)错误标识的信息改正过来后放入模型训练,模型能成功识别。综上所述,说明所构建的模型在波形分类的能力上稳定性较好。

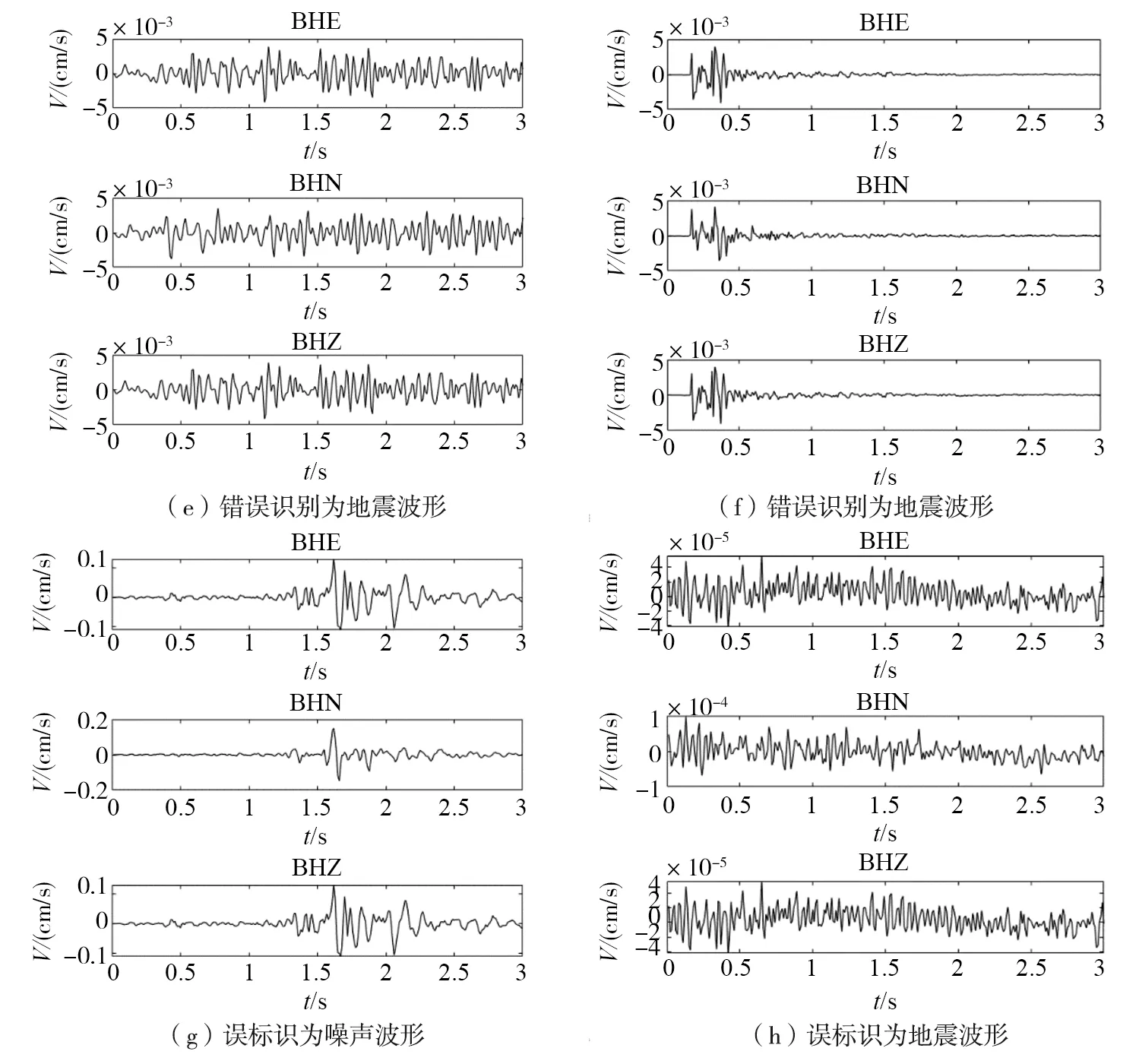
图6 四种波形分类的例子Fig. 6 Examples of the four waveform classification

3.3 其他AI模型分类结果分析

利用文中SW-CNN模型所使用的样本数据,分别采用深度学习中的Alex Net模型和VGG16模型对地震波形进行分类,并与上述SW-CNN模型分类结果进行比较。

3.3.1 Alex Net

Alex Net模型是由KRIZHEVSKY等[3]提出的,其中模型包含了6亿3 000万个连接,6 000万个参数和65万个神经元,主体结果由5个卷积层、3个池化层和3个全连接层组成。为了避免网络训练时出现过拟合的情况,KRIZHEVSKY等加入了LRN层、以及在全连接层后加入Dropout层,使模型更加的鲁棒,从而让模型能更好的进行学习。表5为Alex Net对四种波形的分类结果,可以看出：Alex Net模型在训练集和测试集的识别率均在95%以上。

表5 Alex Net模型对四种波形的识别准确率Table 5 Recognition accuracy of Alex Net model for four waveforms

3.3.2 VGG Net

VGG Net是由SIMONYAN等[4]一起研发的深度卷积神经网络模型,通过多个3×3的卷积核和2×2的最大池化层成功的构建了16～19层的网络结构。由于VGG Net的深度较深,卷积层数量多,因此计算量比较大并且耗费时间较长。相比于Alex Net模型,VGG Net取消了LRN层,用更深的网络和小卷积核来减少过拟合的情况。表6为VGG Net对四种波形的分类结果,可以看出VGG Net模型在训练集和测试集的识别率均在96%以上。

表6 VGG Net模型对四种波形的识别准确率Table 6 Recognition accuracy of VGG Net model for four waveforms

3.4 震例预测结果分析

为了更好的验证模型的优良性,本文对中国境内的2018年7月12日福建明溪和2018年11月26日台湾海峡发生的两次地震分别进行波形在线模拟测试,如图7所示(红色标记为模型所拾取的P波),模型能拾取到震中距在100 km内的地震,并且还能拾取到震中距在100～280 km之内的地震,说明了模型具有一定的泛化能力。与传统的人工拾取相比,卷积神经网络模型在训练样本充足的情况下能拾取到更加复杂和距离更远的地震波形,相信在未来能发挥更大的优势。

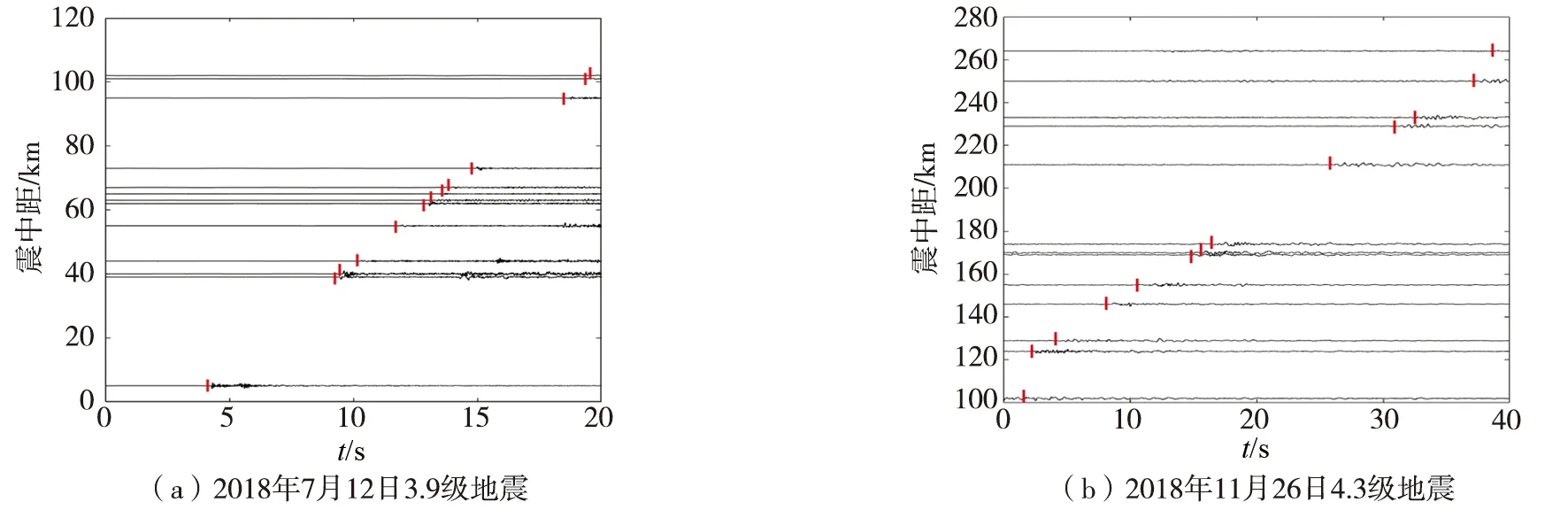
图7 模型对二次震例的测试结果Fig. 7 Test results of the model for secondary earthquake cases

4 讨论与结论

本文提出了一种新的用于地震波形分类的卷积神经网络模型,结果表明：SW-CNN模型对地震、噪声、爆破和异常波形的识别率均在97%以上。本文收集并处理了2012—2017年福建省、台湾省及周边邻省测震台网所记录的数据作为研究样本,共有27 500条三通道波形样本,其中训练集占80%;测试集占20%。将波形分类当成四分类问题,将长3 s的三通道波形应用于卷积神经网络模型中,对卷积神经网络模型的搭建上采取了对比试验,最终选择的是6层卷积层和2层全连接层的网络结构模型。并在3.3小节中展示了其他AI模型对四种波形的识别率.,可以看出其他AI模型的识别率均在95%以上。通过本研究对地震、噪声、爆破和异常波形分类可获得如下小结：

1) SW-CNN模型在独立的测试集中对地震、噪声、爆破和异常波形的识别准确率分别为97.9%、99%、99.2%和99.3%,与文中其他AI模型相比,SW-CNN模型在时效性和准确性上更优。

2) 明显看出：SW-CNN、Alex Net和VGG Net模型对爆破和异常的识别率上优于地震,可能是震级较小的地震或震中距较远的台站地震记录相比于爆破更容易被噪声淹没,导致这些地震记录被误判别成爆破。

3) 对中国境内2018年7月12日福建明溪和2018年11月26日台湾海峡发生的两次地震分别进行波形在线模拟测试,结果表明：模型能很好的拾取到震中距在100 km内的地震,并且还能拾取到震中距在100～280 km之内的地震,说明了模型具有一定的泛化能力。

综上所述,可以利用深度学习中的卷积神经网络强大的分类性能对地震波形进行分类识别,这能够降低地震预警的误识别率,在满足地震波形分类的精度的要求,进一步提高其准确性和稳健性,然后将其应用于实际地震预警与日常地震监测中。

致谢：感谢福建省地震局提取宝贵的地震观测数据,感谢审稿专家所提出的修改意见,感谢编辑部工作人员的支持!