中国地震台网面波震级与矩震级的统计关系

沙海军 吕悦军（中国地震局地壳应力研究所，北京 100085）

中国地震台网面波震级与矩震级的统计关系

沙海军 吕悦军
（中国地震局地壳应力研究所，北京 100085）

为进行地震定量分析，国内外地震学家开展了面波震级与矩震级(地震矩)的关系研究。考虑到我国地震台网测定的面波震级与国外存在一定差异，国外关于面波震级与矩震级关系的研究成果，在我国应用时尚需要论证其适用性。国内相关的研究由于5级以下和6.5级以上地震样本较少，其统计关系的应用范围受到限制；另外，由于未能给出经验关系的标准差等参数，导致无法评估计算结果的不确定性。

为建立适用于中国及邻区的面波震级与矩震级的统计关系，拟利用1990—2014年中国地震台网地震目录中的面波震级和全球矩心矩张量(GCMT)项目提供的相应矩震级数据，使用加权最小二乘法，统计得到了面波震级与矩震级的经验关系式及其标准差。

从1990—2014年中国地震台网目录和GCMT矩震级目录中，挑选出同时具有MS7震级和矩震级数据的地震，共得到806次面波震级大于等于4.5级的浅源地震数据，其中，4.5～4.9级300次，5.0～5.9级390次，6.0～6.9级104次，7.0～7.9级10次，8.0～8.5级2次。由于小震级样本量远大于高震级样本量，直接使用最小二乘法进行统计回归分析，会使统计关系式主要受控于小震级样本，导致在高震级处的较大偏差。为解决这个问题，拟采用加权最小二乘法，使各震级档的样本对统计偏差的贡献率基本一致。

为体现在整个震级范围内矩震级与面波震级的关系，本研究使用了二次函数关系式作为新的统计关系表达式：

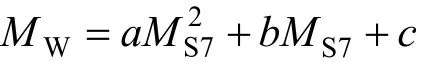
式中，MW为矩震级；MS7为面波震级；a、b和c为待定参数。

采用该关系式，使用加权最小二乘法对数据进行统计回归，得到新的统计关系式、均方差及相关系数

如下：

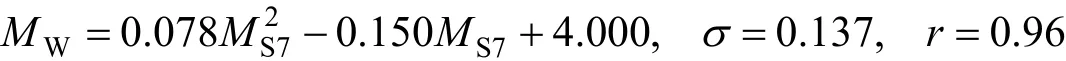
式中，σ为标准差；r为相关系数。

对比了本文与陈培善等(1989)、Ranjit Das等(2011)、陈宏峰等(2014)的统计关系(图1)。陈培善等(1989)和Ranjit Das等(2011)的统计结果较为一致，但相对统计样本偏高。而陈宏峰等(2014)统计直线靠近统计样本的下界，其计算结果偏低。本文的统计曲线基本位于统计样本分布区的中线上，表明其与中国地震台网的实际地震资料更为相符。

在地震定量分析中，矩震级已经逐渐取代面波震级等震级标度。对于中国及邻区的4级以上地震，全球矩心矩张量(GCMT)项目发布的矩震级数据并不完整，对于没有矩震级数据的地震，推荐使用本文的统计关系式，进行面波震级到矩震级的转换。

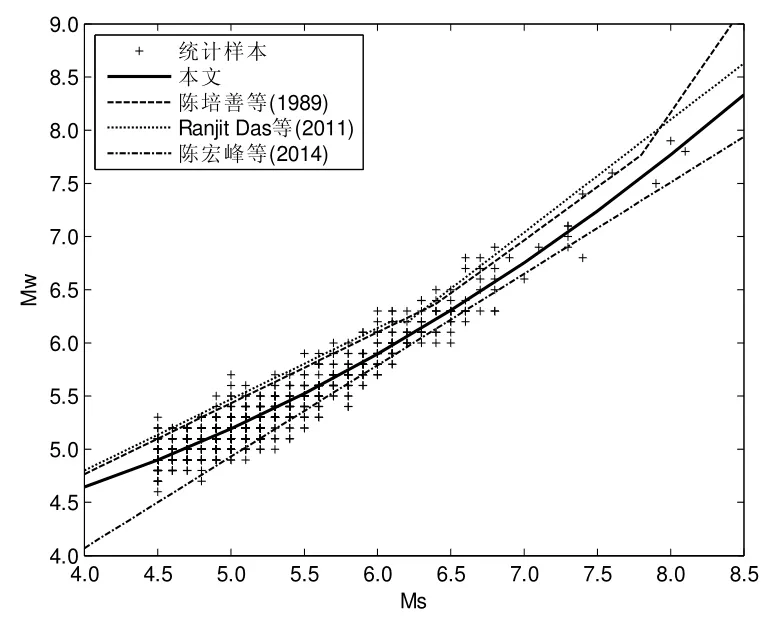
图1　本文与陈培善等(1989)、Ranjit Das等(2011)、陈宏峰等(2014)的统计关系对比