随机侧风下桥塔区域中高速列车气动特性分析

杜礼明,章芝霖,张文岚,李梓豪

(大连交通大学 机车车辆工程学院,辽宁 大连 116028)

高速列车通过桥塔时,由于桥塔遮风,列车周围气压、气流速度发生改变,车体表面的气动载荷发生明显变化,从而导致列车脱轨和倾覆。近年来,国内外学者对不同运行条件下的列车气动特性展开了研究。针对列车附近流场结构,王磊等[1]发现运行条件相同时,列车不同部位流场结构不同,头部、尾部附近流场结构变化严重,但中间列车周围流场分布规律基本稳定;王希理等[2]发现列车背风侧的流场是由列车顶部和底部卷起形成的多个旋涡组成的;谢红太[3]发现随着风速的变化,列车周围流场分布结构复杂不规律,但当侧风情况较为严重时正压区主要分布在迎风侧,并与背风侧产生巨大压差;Xia等[4]分析了大长细比列车附近流场中旋涡的变化,发现每个大尺度流向涡在大小上呈现出交替增加/减少以及横向和垂直方向上的振荡行为。同时,学者们分别采用仿真模拟和风洞试验等方法探讨了不同运行条件下列车气动载荷变化。王玉晶等[5]发现不同车厢气动载荷的时域变化规律不同;李田等[6]采用同一风场模型进行了数值研究,结果发现不同风速下气动载荷系数波动幅值相差较大;王政等[7]通过改变风模型来比较均匀风模型和指数风模型对列车风载荷大小的影响,结果表明不同风场模型下列车气动载荷变化明显不同,列车侧向力和气动力矩差异更明显,指数型风模型下比均匀风模型下大18%;刘智超等[8]发现在相同车速下,列车气动载荷相等,但随着加速度的改变,侧向力、阻力、倾覆力矩的变化率不断增大,导致短时间内高速列车气动载荷的变化增大;曾广志等[9]发现在龙卷风下列车背风侧的压力系数较迎风侧更为显著。

自然界的风受山川、地形和建筑物等的影响,风速往往是瞬变的,但目前对高速列车流场结构的研究大多是以风速恒定为前提的,未考虑在桥塔遮蔽的风场中,风速波动对高速列车气动性能的影响,因此,研究结果难以准确反映实际情况。本文采用 “Chinese Hat”随机侧风模型,从压力和涡量两个角度对比分析恒定侧风和随机侧风工况以及不同平均风速的随机侧风工况下列车周围流场变化,总结随机侧风下列车在桥塔环境中的气动特性,为桥塔区域的安全行车提供参考。

1 列车-桥系统的气动仿真模型

1.1 列车-桥塔耦合的计算域

为确保计算结果受边界影响较小,计算域设置为:列车上方流场、侧方流场为车宽的5倍以上,后方流场为车宽的20倍以上;截取部分桥梁,取计算域长400 m,高29.2 m,宽200 m[10]。本文以某跨江大桥为研究对象,保留桥梁塔柱断面轮廓,桥塔宽21 m,不考虑受电弓、转向架、裙板等结构,建立头-中-尾3节编组形式的列车-桥气动仿真模型。由于掠过列车气流速度比音速低0.3 Ma,可视为不可压缩[10]。基于动态网格方法,采用滑移网格技术模拟车体运动,采用局部动态层变法更新动态网格,因此所有工况采用瞬态计算。

1.2 网格剖分与边界条件设置

采用嵌套网格技术划分计算域的网格,车体附近为四面体网格,其余部分为六面体网格,总数约454 万。桥塔区域的网格划分见图1。

图1 桥塔区域的网格划分

计算域边界条件设置见图2:流体域中自然风入口为速度入口;前、后表面和自然风出口为压力出口;上、下表面为对称面;车体和桥梁表面为无滑移壁面。湍流模型选用k-w模型[11],用Simplec算法耦合速度压力,计算时间步长为2×10-3s,采用二阶迎风格式进行求解。

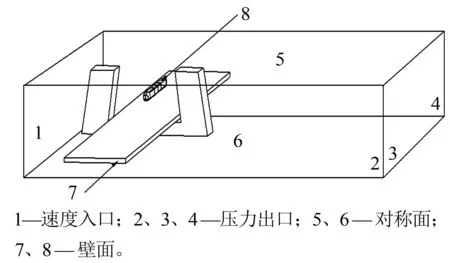
图2 计算域边界条件

1.3 风场模型

将恒定侧风视为风速为15 m/s且方向垂直于列车侧墙的均匀气流,采用修正的“Chinese Hat”阵风模型描述随机侧风。“Chinese Hat”动态风场是在欧盟铁路互联互通技术规范(TSI)中提出的[12],其风速数值变化按周期循环,一个周期分为7个阶段,围绕平均风速上、下起伏。图3为平均风速为15 m/s时 “Chinese Hat”风速模型的风速变化曲线。第一阶段风速由0增长至平均风速,增长了0.312 5 s;第二阶段风速保持在15 m/s不变;第三阶段从0.625 s开始,风速变化呈曲线增长,在0.937 5 s时达到峰值,为22.26 m/s;第四阶段风速减小,在1.25 s时下降至平均风速;第五阶段以平均风速持续作用0.625 s,完成内风速变化;第六阶段从1.875 s开始,风速下降,在2.187 5 s时降到谷值,为3.8 m/s;之后进入第七阶段,最终风速在2.5 s时回到平均风速,完成一个风速变化周期,之后进入下一个循环周期。由于每个周期内风速变化趋势相同,本文选取一个风速周期内气动载荷、空气压力、空气涡量进行分析。当平均风速增大时,风速曲线上每一时刻对应风速增大,反之减小,但风速阶段变化趋势不变。

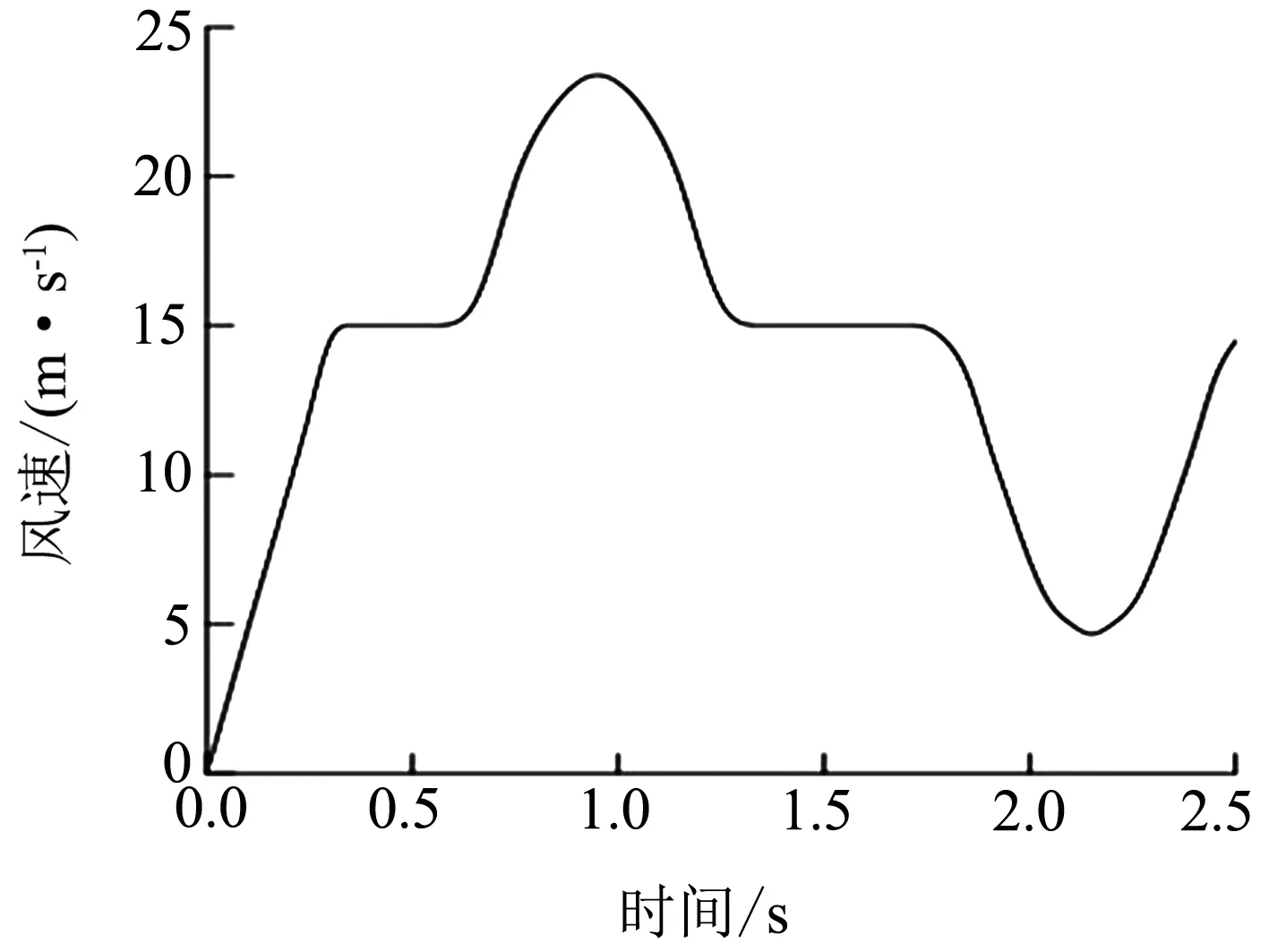
图3 “Chinese Hat”阵风的风速随时间变化曲线

本文设计了5种工况(表1),对比分析相同车速下,风模型对列车气动特性的影响。

表1 模拟工况

1.4 验证模型可靠性

为验证气动模型的准确性和仿真计算方法的可行性,保证后续结果的准确可靠,本文建立的几何模型和计算工况与文献[5]相同。在此条件下,对比分析列车所受的横向力,仿真结果与参考值对比见图4,从图4中可以看出,两者的吻合较好,由此表明,本文的数值模型和数值方法可行。

图4 仿真结果与参考值对比

2 不同风场模型下车体表面压力特征

自然风与列车风的耦合作用引起列车表面的气压、气动升力、横向力等发生变化,对列车运行安全产生影响。为分析风模型对列车气动性的影响,取头车经过桥塔中央时刻,即第1.5 s(此刻随机侧风经过前4个阶段变化,风速进入平稳状态),比较此时头车周围空气气动压力,气动压力变化见图5。两种风模型下,头车横截面周围低压区在头车中心附近,压力增长呈现以头车为中心,向四周增大的趋势,且都为正压,气动压力变化现象明显。随着随机侧风平均风速的增大,头车周围低压区向迎风侧移动。比较图5(d)、图5(e)可知,列车横截面发生这种变化后与恒定侧风下极为相似。图5(e)中,恒定侧风下压差是随机侧风下的1.12倍。由空气气动压力分布推断,风模型因素对列车周围空气压力变化趋势影响有限。

(a)工况1

3 不同风模型下涡量场特征

每个流体元都有独立的运动状态,因此流体运动时会发生变形,本文用既能直观反映旋转的角速度和又能反映平动的线速度的涡来描述列车周围空气的运动状态。取两种风模型下和不同平均风速的随机侧风下涡的运动和涡量变化进行对比。

比较涡量变化之前,取第1.5 s时,根据头车周围空气流线变化对涡的分布进行比较,图6为两种风模型下列车周围流线分布图。比较图6(b)和图6(e),平均风速都为15 m/s时,恒定侧风下头车附近空气从上、下两侧绕过头车;随机侧风下,空气在头车上方分两个方向流动,迎风侧上方出现空气流动形成的涡的趋势。可见,较恒定侧风,随机侧风由于每时每刻风速数值不同,空气流动形式比恒定侧风更为复杂,这与文献[2]所得结论相吻合。针对随机侧风模型,进一步讨论平均风速变化对列车周围空气流动的影响。由图6(a)～图6(d)可知,当平均风速为10 m/s时,头车附近暂时没有出现涡,但头车上方空气分两个方向流动;平均风速为15 m/s时,头车上方、迎风侧空气流动各分两个方向流动,头车迎风侧上方出现一个涡;平均风速为20 m/s时,头车上方空气流动方向的分界线由头车正上方逐渐移动到迎风侧,列车下方附近流线更密集;平均风速为25 m/s时,头车上方、迎风侧、背风侧出现共计6个涡,且这6个涡关于列车纵轴线呈对称分布。随机侧风平均风速增加,旋涡数量增加的速度也越来越快。从涡的数量和涡出现的位置推断,平均风速越快,头车周围空气运动越复杂,该结果与头车周围空气气动压力变化规律相吻合。

(a)工况1

由于在没有漩涡的地方,涡量也未必是小量,因此取第1.5 s时,对头车周围的涡量进行分析,两种风模型下列车周围涡量分布见图7。当平均风速相同时,在距离车体较近的位置,随机侧风下,头车周围最大涡量为3.803 59 s-1,恒定侧风下为0.941 511 s-1,随机侧风下周围涡量是恒定侧风下的4倍左右。进一步比较不同平均风速的随机侧风下的涡量大小,距离列车越近,涡量越大,当平均风速为10 m/s时,最大涡量为2.906 08 s-1;平均风速为15 m/s时,最大涡量为3.803 59 s-1;平均风速为20 m/s时,最大涡量为5.566 48 s-1;平均风速为25 m/s时,最大涡量为8.911 68s-1。综上所述,随着平均风速的增大,最大涡量呈现指数型增长。

(a)工况1

4 不同风模型下的气动载荷

高速列车的非均匀气动载荷会加剧列车蛇行,导致列车安全性参数变差。列车的脱轨与侧翻发生时间很短,可以认为是瞬间完成的,因此本文选取头车气动载荷最大值进行分析。

为探究随机侧风对列车气动载荷变化的影响,分析随机侧风平均风速增加对列车气动载荷变化程度的影响,取列车运行过程中头车气动载荷绝对值最大值,形成图8所示曲线。由图8(a)可见,升力、 横向力变化范围和数量级一致,比侧滚力矩高一个数量级;由图8(b)可见,点头力矩、摇头力矩数量级一致,但点头力矩的变化范围高于摇头力矩,且同一平均风速下,点头力矩是摇头力矩的1～3倍。总体上,在同一车速下,气动载荷最大值整体呈现随平均风速升高而增加的趋势。其中,升力最大值、横向力最大值、侧滚力矩最大值、摇头力矩最大值增速随平均风速增大而增加,近似指数型增长。而点头力矩最大值增速较为平缓。气动载荷最大值随平均风速升高而增大,但不同类型气动载荷升高速率不同,点头力矩增速最为平缓,应考虑不同气动载荷的综合作用,不应仅考虑单一气动载荷变化。

(a)气动力

在随机侧风下,为从时域角度探究气动载荷与平均风速增加之间的关系,分析列车经过桥塔全过程时的气动载荷变化,见图9。从图9可知,同一时刻,列车气动载荷随平均风速变化幅度较小,变化趋势较为杂乱,变化幅度与平均风速增加幅度之间没有明显关联。但在整个行驶过程中,分别比较图中每个载荷变化的曲线却可以发现,随着平均风速的增加,气动载荷峰值、谷值幅度加大,且峰值、谷值数量增多,尤其是在0.8～1.0 s和1.8～2.0 s(列车进出桥塔区域的时间)。图9(b)、图9(c)中,两个时间区间内,横向力、侧滚力矩在原方向上骤然增大约10%,可见虽然列车运行过程中经过桥塔遮蔽区域,但对于整个行驶过程而言,由于桥塔区域太短,即便平均风速增大,桥塔遮风作用对气动载荷随时间变化剧烈程度加剧作用基本没有体现,该结果与参考文献吻合。

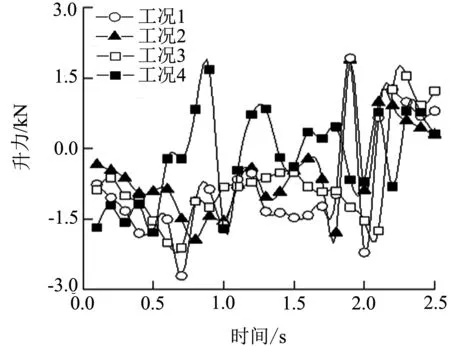
(a)升力

可见,列车运行过程中,在随机侧风工况下,随着平均风速的增大,气动载荷变化剧烈程度加大。不同类型气动载荷增加幅度不同,宽度小于车厢长度的桥塔对缓解列车气动载荷增加和随时间起伏剧烈程度现象作用不明显,在既有线路下,列车安全运行应充分考虑实际风速波动现象。

5 结论

(1)风模型因素对列车周围气动压力变化影响有限。随机侧风模型中,随着平均风速增大,头车周围正、负压分界线向迎风侧移动。

(2)风模型变化对涡的影响明显。平均风速相同时,随机侧风下最大涡量是恒定侧风下的4倍左右,且最大涡量呈现指数型增长。随机侧风下,平均风速越高,列车附近空气流动形成的旋涡越多,旋涡数量的增速也越来越快。

(3)平均风速相同时,随机侧风对列车气动载荷影响更大。随机侧风下,随着平均风速的增大,气动载荷变化剧烈程度加大,且不同类型气动载荷增加幅度不同。