基于改进灰色Markov模型的建筑物沉降量预测

王洪德,李骞

(1.大连交通大学 交通运输工程学院,辽宁 大连 116028;2.辽宁省隧道工程与灾害防控专业技术创新中心,辽宁 大连 116028)

地铁车站深基坑施工过程会对周围地层产生扰动,从而对周围建筑物造成沉降或倾斜,影响建筑物的安全和正常使用。因此,必须采取有效措施对施工引起的地面沉降进行监测和预警[1-4]。采用准确、有效的科学手段对深基坑周边建筑物的沉降量进行预测,不仅能够减轻甚至规避风险,同时对复杂系统预测方法的研究具有重要的推动作用[5-8]。

目前,国内外学者对深基坑开挖引起周边建筑物沉降的预测方法进行了很多尝试。Miliziano等[9]采用一个简单的理想弹塑性本构模型,利用数值分析的方法获得沉降预测值;Khosrojerdi等[10]利用参数研究的结果进行回归分析,建立RSF最大沉降量的预测方程;马征等[11]结合多智能体粒子寻求最小二乘法支持向量机,对昆明市某基坑开挖过程中周围建筑物的沉降进行预测;沈简等[12]采用双曲线法、指数曲线法和灰色理论等方法对基坑周边坡顶的建筑物沉降进行了预测;章红兵等[13]结合土体变形空间分布规律,通过经验系数将土层性质、周边施工情况纳入考量,提出了考虑基坑开挖空间效应的邻近建筑物沉降预测方法。以上这些预测方法,在不同程度上对深基坑施工引起周边建筑物沉降的防范提供了技术支撑。然而,通过深基坑开挖的工程实践并结合国内外相关文献的分析发现,对于小样本的监测数据量,已有的预测方法在实际应用过程中,经常出现预测精度和偏差过大的情况,如灰色预测模型在中长期预测应用中出现的偏差越来越大。

鉴于此,本文结合某地铁车站深基坑工程实际,以灰色模型为基础,先对其进行改进,然后通过Markov误差修正,建立改进的灰色Markov模型,实现对深基坑施工引起周边建筑物累积沉降的预测研究,以期确保工程施工安全可靠。

1 建筑物沉降量预测模型的建立

1.1 改进灰色模型的建立

灰色模型是对原始数据序列进行累加,对于诸如建筑物沉降这种小样本数据集的分析,存在较大的精度误差。为提高中长期预测的准确性,在灰色模型的基础上,通过对原始数据指数化处理,给出具体数据处理方法:

x(0)(k)=Aeu(k-1),k=1, 2, …,n

(1)

式中:x(0)(k)为指数化处理后的初始累积沉降数据序列;u为指数化处理后的发展系数;A为指数化处理后的灰色作用量;k为指数化处理后的初始累积沉降监测数据序号。

一次累加后:

(2)

式中:x(1)(k)为初始累积沉降数据序列一次累加生成的序列。

以此为基础,建立微分方程,用最小二乘法进行估计,得出u,A的估计值:

(3)

式中:a为灰色模型的发展系数;b为灰色模型的灰色作用量。

基于此,建立初始数据序列模型:

(4)

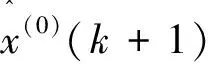
1.2 相对误差状态划分

改进灰色Markov模型的重要一步在于转移概率矩阵的计算,只有得到转移概率矩阵,才能知道预测值的修正方向,从而进行Markov误差修正,使预测值更加贴近真实值。为了得到转移概率矩阵,首先需要进行预测值与真实值之间相对误差的状态划分。

通过改进的灰色预测模型求取各观测点的预测值,将实测数据与预测数据的相对误差作为Markov修正的初始数据序列,以此进行状态划分。具体方法是以该数列中心点为基准线,分别向上和向下做累积m条横线,从而将初始数列划分成m+1个状态区间[14]。

1.3 转移概率矩阵

通过转移概率矩阵可以看到相对误差的每一种状态转移到其他状态的概率,从而确定预测值修正的方向。

第一步状态转移概率矩阵中,若发现第i行的转移概率相等,则可用更多步的状态转移概率矩阵。由状态区间Ej经过k(k=1,2,…,n)步转移到状态区间Ei的初始数据个数为Mij(k),处于Ei的初始沉降数据的个数为Mi,则经过k步转移的状态转移概率为:

(5)

式中:pij(k) 为由状态区间Ej经过k步转移到区间Ei的概率;Mij(k) 为由状态区间Ej经过k步转移到区间Ei的数据个数;Mi为处于状态区间Ei的初始沉降量数据个数。

经过k步的状态转移概率矩阵为:

(6)

1.4 误差修正

观察状态区间的转移方向,进行Markov误差修正得出最终的累积沉降量预测值。Markov误差修正为:

(7)

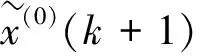
1.5 模型的检验指标

针对预测值与真实值之间的联系与评价,相对误差可以表示预测结果偏离真实值的实际大小,而且更能反映预测的可信程度。由于预测数据不止是一组,所以选择相对误差作为指标之一:

(8)

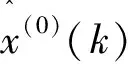
灰色模型的检验方法可以采用后验差检验,后验差检验包含后验差比值C和小误差概率P′[15],这是对残差分布的统计规律检验。首先要求出建筑物累积沉降量数据序列与预测值的残差和相对误差,相对误差的计算见式(8),残差的具体计算为:

(9)

式中:E(0)(k)为第k个数据的残差;n为初始数据的组数。

得出残差之后,求出初始数据的均值和残差均值为:

(10)

(11)

结合式(10)、式(11),可求其方差和残差方差:

(12)

(13)

将后验差比值、小误差概率、相对误差作为模型检验指标:

(14)

式中:C为模型的后验差比值。

(15)

式中:P′为模型的小误差概率。

对应的检验指标的精度等级评定见表1。

表1 精度检验表

结合表1,后验差比值C越小,表示预测出来的建筑物累积沉降量越精确。小误差概率P′越大,表示模型预测出来的建筑物累积沉降量分布越均匀。

2 模型应用

记录某地铁车站周边建筑物在基坑开挖过程中累积沉降量的数据。地铁车站位于市内繁华地段,地下为多套地层力学性质差异较大的复杂场地,并存在微承压水,地层结构对地下工程有较大影响。选取建筑物上靠近基坑一侧的角点JCJ06,给出5月25日～7月2日的30组(日期不连续是因为当日没有监测,并不影响试验研究)建筑物累积沉降量监测数据,见表2。

表2 建筑物累积沉降量监测数据

由表2可以得出,建筑物累积沉降量的平均值为-40.16 mm,沉降最多时发生在6月22日,向下沉降了2.24 mm。

2.1 改进灰色模型的拟合

基于表2所列的建筑物累积沉降量实测数值,运用改进的灰色模型进行数值模拟,拟合效果见表3。

表3 模型拟合效果

由表3可以得出,改进的灰色模型模拟数值的平均值为-38.04 mm,与真实数值相差2.12 mm,沉降最多时发生在5月26日,比起上一期向下沉降了0.81 mm。

2.2 状态区间划分

原则上,状态区间划分越详细越好。结合工程实际,经多次试验,同时考虑到状态区间范围更加均匀和相对误差的分散范围,确定将相对误差划分为4个状态区间,见表4。

表4 误差状态区间表

2.3 转移概率矩阵

为了得到转移概率矩阵,需对不同状态区间的个数和转移趋势进行统计和观察。结合表3和表4可以看出,相对误差处于状态E1的个数为3个,处于状态E2的个数为7个,处于状态E3的个数为12个,处于状态E4的个数为3个。通过观察状态区间的转移趋势可知,处于状态E1的相对误差下一次转移到状态E1,E2,E3,E4的个数分别为2,1,0,0。处于E2状态的相对误差下一次转移到状态E1,E2,E3,E4的个数分别为1,4,1,1。处于E3状态的相对误差下一次转移到状态E1,E2,E3,E4的个数分别为0,1,10,1,。处于E4状态的相对误差下一次转移到状态E1,E2,E3,E4的个数分别为0,0,1,2。

根据式(5)和式(6),得出一步转移概率矩阵:

2.4 Markov修正

6月27日沉降量的相对误差处于E4状态,根据求出的转移概率矩阵,可以看出,6月28日的沉降量将转移到E4状态。根据误差修正公式,可以求出6月28日的累积沉降量的预测值为-48.56 mm,比实测的6月27日的沉降量增加了0.31 mm。将6月28日的预测值作为原始数据代入改进的灰色模型进行预测,可以得出6月29日的预测值,重复上面步骤,根据相对误差进行状态划分并做出转移概率矩阵,并再一次进行Markov误差修正。以此类推,预测出后5天的沉降量,模型预测结果见图1。

图1 模型预测结果

由图1可知,改进的灰色Markov模型的预测值平均值为-49.97 mm,改进的灰色模型的预测值平均值为-48.89 mm,而原始值的平均值为-51.04 mm,表明改进的灰色Markov模型的预测值明显更贴近实测值。

3 模型精度评价

按照前文所述模型检验方法,采用相对误差作为检验指标。在改进的灰色Markov模型中,由于每一次预测都需要重新进行状态划分和误差修正,所以每一次只能预测一个值。将5次预测出来的结果与用改进的灰色模型得出的结果进行相对误差的比较,并求取5次相对误差的平均值,模型精度对比见表5。

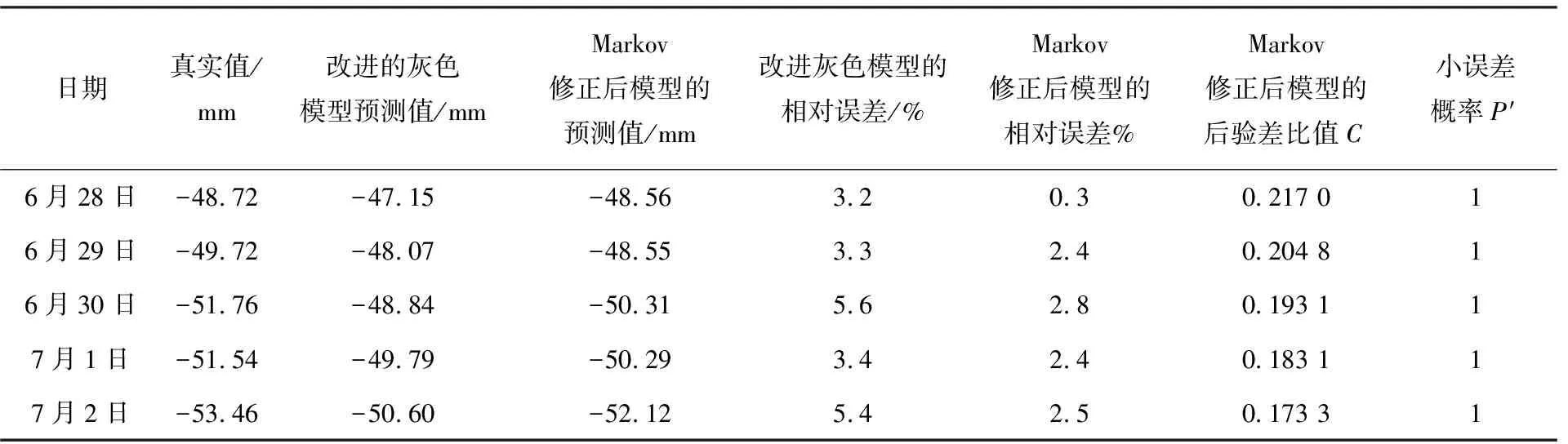
表5 模型精度对比

从表5的计算结果可以看出,每一次预测出来的精度都得以提高,改进的灰色Markov模型的平均相对误差为2.1%,而改进的灰色模型的平均相对误差为4.2%,表明修正之后的模型在相对误差上精度提高了2.1%。修正之后模型的后验差比值逐渐减小,说明修正后的模型在后期预测的数值与实际值离散程度相对较小,从而进一步验证了修正后的Markov模型在中长期预测当中比改进灰色模型更加精确可靠。

4 结论

针对改进的灰色Markov模型,对地铁车站深基坑施工引起周边建筑物累积沉降量进行预测,得出结论如下:

(1)通过对灰色模型的改进(指数化处理传统模型中的发展系数为u、灰色作用量为A),优化预测序列的总体误差,建立了改进后的灰色模型。

(2)转移概率矩阵的建立是改进灰色Markov模型的重要一步,通过转移概率矩阵可以看到相对误差的每一种状态转移到其他状态的概率,确定预测值修正的方向,最后运用Markov误差修正得到最终预测值。

(3)改进的灰色Markov预测模型可用于小数值样本数据集仿真分析,其预测相对误差对比原改进灰色模型由原来4.2%下降到2.1%,从而使得深基坑施工引起周边建筑物累积沉降的预测更加贴近实际。