基于车辆弓网双耦合的受电弓随机振动疲劳分析

杨雨晨,王悦东,于春洋

(1.中车大连机车车辆有限公司,辽宁 大连 116028;2.大连交通大学 机车车辆工程学院,辽宁 大连 116028;3.中车长春轨道客车股份有限公司,吉林 长春 130062)

受电弓是高速列车唯一的受流部件,随着列车速度的攀升,受电弓的工作环境日趋恶劣。为保证受电弓有良好的工作状态,对受电弓进行疲劳强度研究是非常必要的。

目前,国内外学者对受电弓系统进行了大量研究,Montserrat等[1]、Jorge等[2]、Petter等[3]对弓网动态接触进行了大量试验,得到弓网接触各项数据,同时揭示了受电弓系统关键频率范围,为受电弓疲劳强度研究提供了有力支持;关金发等[4]基于实测数据建立了高精确度的受电弓动态仿真模型,为更加高效获取弓网动态数据提供了有效手段。基于上述研究,为了进一步揭示多源振动对受电弓结构性能的影响规律,宦荣华等[5]基于随机平均法研究了计及车体振动的弓网动力学响应;杜子学等[6]基于固定界面模态综合法建立刚柔耦合多体动力学模型,并采用准静态应力叠加法对受电弓进行疲劳分析;贾荣等[7]基于二质量模型获取受电弓等效参数,进而获得结构力学响应,并采用Goodman曲线评估受电弓焊缝疲劳强度;Qi等[8]基于弓网模型利用拉格朗日与Newmark方法建立动力学方程,并对受电弓关键部件进行疲劳谱分析;Jia等[9]根据模拟及疲劳试验数据,提出了一种改善后端绝缘子组设计结构的方法,解决了受电弓部件界面应力集中的问题。上述针对受电弓结构的疲劳研究中,多采用静力加载和线性累加的方式对受电弓进行疲劳评价,但受电弓在运行中处于变载荷工况,传统准静态加载与实际有一定差距;除此之外,基于试验数据开展受电弓疲劳性能评估,虽结果较为准确,但时间与经济成本较大,因此,开展兼顾低成本与评估结果合理性的受电弓随机振动疲劳研究,对实际运用具有十分重要的意义。

本文基于车辆弓网双耦合的方法,建立多频谱加载的疲劳寿命模型,评估受电弓在多点随机振动激励下的疲劳寿命,进而结合实测弓网振动数据与IEC 61373:2010标准中规定的载荷谱[10],进行多PSD谱分析,并基于谱分析结果,利用Dirlik法对受电弓进行随机振动疲劳评估。

1 受电弓随机振动数值表述方法

1.1 随机振动

随机振动作为普遍存在的一种机械运动,在铁路车辆中也多有发生,如弓头受到弓网间不规则激励产生的振动。因随机振动的不规则特性,其振动形式无法利用明确的模型加以描述。但文献[11]的研究表明,随机振动激励具有明显的统计规律,可利用概率统计理论表述其振动特性。目前,随机振动的分析方法主要分为时域法和频域法,与前者相比,频域法因其物理意义明确且计算简便而被广为使用。功率谱密度函数作为随机振动的一种频域分析方法,将随机振动的时域数据转换为频域数据,并表征了随机振动过程中的能量变化。

1.2 功率谱密度(PSD)分析

功率谱密度函数是一种时域信号的频域描述,根据帕塞瓦尔定理,能量守恒是时域与频域相互转换的重要前提,二者之间的关系为[12]:

(1)

式中:Fx(ω)是x(t)的傅里叶变换;ω为圆频率。

将式(1)对时间取极限,得到时域函数的频域形式为:

(2)

功率谱密度函数Sx(f)为:

(3)

式(3)的意义在于能够从能量角度体现信号的能量(平均功率)在频域上的分布规律。在转换后的坐标系中,Sx(f)与横轴f所围成的面积就是这个信号携带的总能量或平均功率,即x(t)幅值分布的方差或均方值。由式(3)可知,当x(t)表示加速度随时间的变化时,Sx(f)就是加速度功率谱密度。

2 受电弓随机振动疲劳分析方法

2.1 Dirlik法

受电弓在随机振动激励下会发生随机振动疲劳破坏。目前已经有多种研究理论,如Lalane、Dirlik、Steinberg、Narrow Band等,它们各有优劣,但普遍认为Dirlik在宽带随机振动疲劳分析中的计算结果更加准确[13],因此本文采用Dirlik法进行疲劳评估。

Dirlik法将两种已知频谱的70种情况经过傅里叶逆变换转换为时域谱,再通过雨流计数法重新进行统计,最后利用一个指数和两个Rayleigh概率密度进行拟合,得到雨流应力变化范围概率密度函数。其雨流应力变化范围概率密度分布模型的表达式为[14]:

(4)

式中:

式中:mi为第i阶惯性矩,用于表征频率谱的平稳性;γ为不规则因子,用于判定宽、窄带随机过程;S为应力范围。

Dirlik累计损伤比表达式为:

(5)

式中:ν为平均功率;T为实验所持续的时长;N(S)为S-N曲线中应力幅值S对应的破坏循环次数。

2.2 带宽系数

基于频域的疲劳分析方法可以分为窄带法和宽带法,在分析中判定随机振动的带宽是重要的一环,不同带宽的随机振动疲劳分析需采用不同的疲劳分析方法,才可以得到精确解。带宽根据带宽系数ε和不规则因子γ确定:

(6)

(7)

对于带宽系数,当ε趋向于0时,为窄带随机过程,当ε趋向于1时,为宽带随机过程。一般认为当ε>0.6时为宽带随机过程;对于不规则因子γ,当γ趋向于0时,为宽带随机过程。从式(6)、式(7)可知,判断随机振动过程是窄带或宽带的决定因素是各阶谱距,谱距的表达式为:

(8)

式中:f为频率;Sx(f)为加速度功率谱密度。

3 受电弓随机振动疲劳分析

3.1 受电弓有限元模型

以某型号受电弓为例,进行基于车辆弓网双耦合的多点随机振动疲劳分析。受电弓是一种铰链式机械构件,由底架、下臂杆、上框架、弓头支架铰接而成,弓头通过弓头弹簧与弓头支架相连。在运行中,弓头碳滑板通过与接触网接触进行电力传输,底架通过绝缘子与车顶固定,受电弓运行示意图见图1。

图1 受电弓运行示意图

为获取受电弓在实际运行工况下的动力学响应,根据某型受电弓物理模型,建立有限元分析模型,见图2。

图2 受电弓有限元模型

为保证仿真分析结果的准确性,根据同一型号受电弓参数[15],校核本文所用模型。在升弓高度为1 600 mm时,各项参数如下:m1为弓头质量,7.51 kg;m2为上框架质量,5.86 kg;m3为下臂杆质量,4.64 kg;k1为弓头弹簧刚度,8 380 N·m。

3.2 实测数据处理

本文提取兴文—乐山成贵场线路、列车时速为250 km/h时的弓网间力-时间实测数据,见图3,加载到受电弓仿真模型弓头处,对弓网振动进行模拟。

图3 实测压力-时间曲线

为满足实测数据与IEC 61373:2010标准相匹配,本文在实测低频采样数据的基础上,对平均压力的数据进行统计,得到该实测数据符合正态分布N(124.83,26.52),生成符合该正态分布规律的随机数,填充到两个采样点数据之间,实现样本数据扩容,进而得到符合频率需求且具有普适性的弓网接触力数据。根据弹性力学理论,对受电弓模型进行整弓弹性模量试验,得到整弓弹性模量,即弓头压力与弓头位移的关系,再根据补充后的力-时间时域谱,结合整弓弹性模量变换为加速度-时间时域谱,取其自相关函数,对自相关函数进行傅里叶变换得到加速度功率谱密度曲线(PSD),见图4。

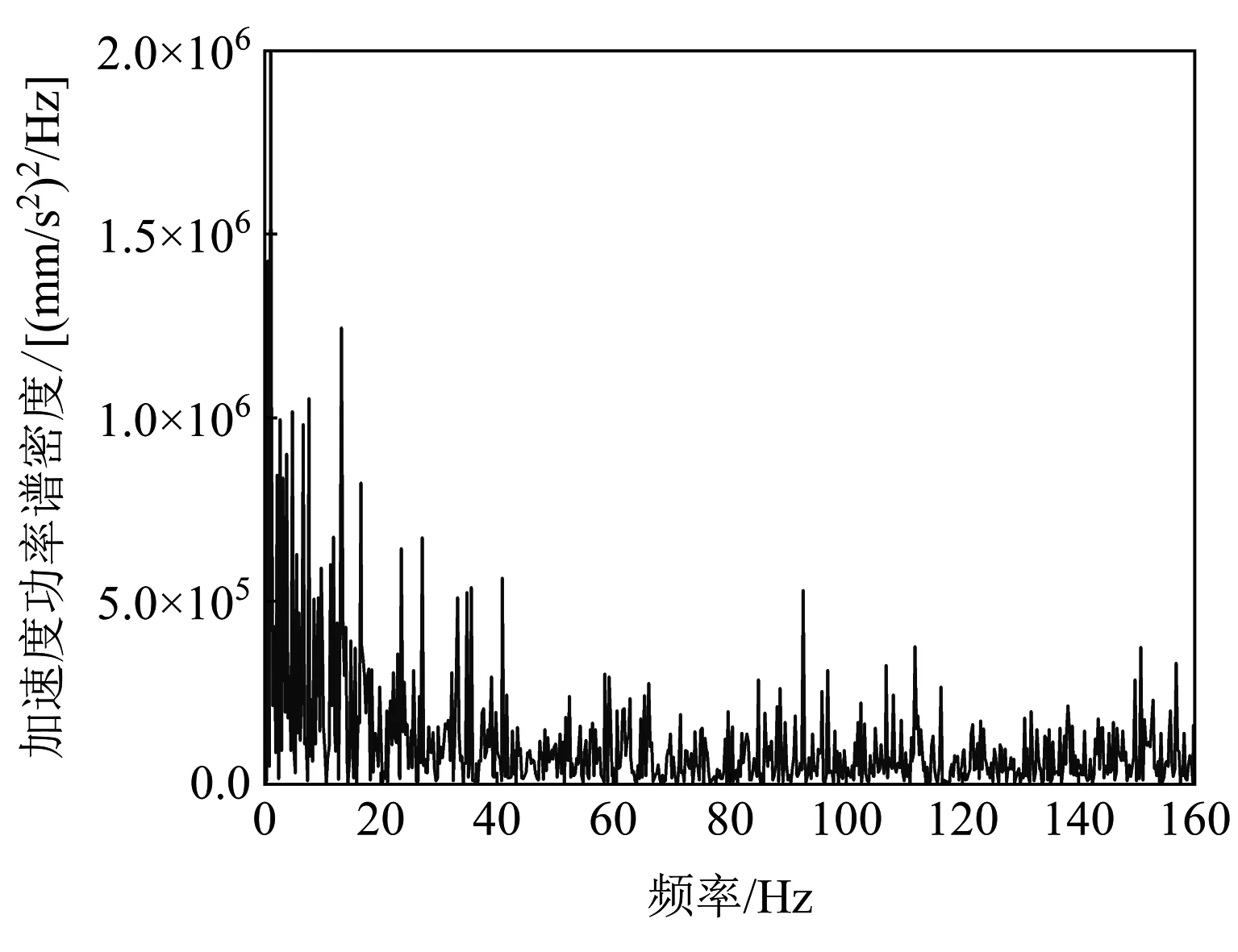
图4 弓头激励PSD谱

3.3 边界条件的施加与计算

受电弓运行时的疲劳性能受到多源振动的影响,其中由车体及弓网间高频冲击振动耦合而成的多点随机振动对受电弓结构影响最为显著[16]。根据文献[17]所述,一条激励谱无法完整描述受电弓动力响应全貌,因此,为了合理获取车体及弓网耦合作用下的受电弓力学响应,根据IEC 61373:2010所提供的车体悬挂设备加速度功率谱参数,对受电弓有限元模型施加边界条件。IEC 61373:2010标准中的加速度功率谱见图5。

图5 加速度功率谱

以受电弓的质量为依据,选定所关注的频率范围为5 ～ 150 Hz,根据受电弓实际运行条件,将标准中车体激励谱加到受电弓与车顶相连的绝缘子处;将基于实测数据生成的加速度功率谱加到弓头碳滑板处,模拟受电弓在实际运行工况下的受力情况。对要施加激励的部分进行约束:弓头碳滑板与接触网接触范围约束Z向线位移,底架安装绝缘子处约束X、Y、Z向线位移,见图6。

图6 施加约束后的有限元模型

为辨析车体激励方向对受电弓疲劳寿命的影响,对其进行只加载车体振动的单点随机振动分析,分别得到受电弓在车体X、Y、Z向激励时的最大Von.Mises应力,见表1。

表1 各方向的最大Von.Mises应力

由表1可知,受电弓结构在车体Z向激励下所得应力最大,即振动对结构影响最强烈,所以本文只分析对比Z向激励下的单点与多点随机振动疲劳。

多点随机振动分析是在车体Z向激励的基础上,在弓头加入Z向功率谱密度谱进行多点随机振动分析,应力云图见图7。

图7 多PSD谱Z向激励下的应力云图

由于受电弓疲劳破坏的常见位置是弓头相关焊缝处[18],所以本文针对受电弓弓头关键焊缝疲劳强度以是否加入车体激励为变量,进行多谱作用与单谱作用分析对比。根据已得位移解计算加速度响应PSD,对比该焊缝中应力最大点的加速度功率谱响应结果,见图8。

图8 多PSD谱Z向激励下的加速度响应谱

由图8可知,针对本文所用受电弓模型的计算,在15 ～ 25 Hz频段,加速度响应强烈,共振明显,且在17.48 Hz时达到峰值;对比单点随机振动的PSD响应谱,多点随机振动在固有频率为17.48、22.53 Hz时振动响应更加强烈。

3.4 疲劳分析

根据3.3节得到的弓头加速度功率谱密度,得到弓头随机激励的各阶谱矩:m0=1.95×1011,m2=7.84×1016,m4=4.43×1022,进而得到该谱的带宽系数,ε=0.54;根据IEC 61373:2010中的载荷谱,可以得到车体随机振动激励的各阶谱矩:m0=1.74×107,m2=1.16×1012,m4=3.77×1017,带宽系数ε=0.89。因此,该随机过程属于宽带随机过程,采用Dirlik法会得到更为精确的结果。

通过随机振动谱分析得到危险点的加速度PSD响应谱,可以求得该响应函数的各阶谱矩,谱矩是计算带宽系数的基础,也是Dirlik疲劳分析方法中计算各项参数的基础,根据IEC 61373:2010试验标准,试验时间为5 h。根据欧洲标准EN 1999-1-3:2003所提供的的铝材焊缝的S-N曲线,见图9。根据危险点所在位置,选取编号为36-3.4的T形焊缝S-N曲线,结合上文所叙述的各项公式进行计算可得累计损伤比。

本文选取一条关键位置焊缝中的10个节点作为评估点,进行分析对比,评估点位置见图9。

图9 评估点位置

根据Dirlik法分别计算未加载车体激励与加载车体激励下相同评估点的累计损伤比,单点随机振动与多点随机振动下的累计损伤比对比曲线见图10。

图10 累计损伤比对比曲线

在加入车体激励后,由于关键焊缝所在位置距离车体激振点较远,且受电弓结构对激励具有一定的削弱作用,而弓头激励距弓头较近,且振动不能被其自身结构吸收,所以弓网激励对弓头的寿命影响较大,但车体振动亦会造成疲劳破坏。因此,在加入车体激励后,弓头关键焊缝各节点的累计损伤比均大于弓头单点激励下的累计损伤比,且该焊缝在多点激励下最大疲劳损伤比为6.41×10-7,在单点激励下最大损伤比为5.90×10-7。由此可知,在此模型下,加载车体激励后对受电弓疲劳损伤的影响占总损伤的比例可达8.6%,因此,虽然弓头焊缝的疲劳损伤主要由弓网间的高频振动引起,但车体振动也不可忽略。

4 结论

(1) 对比该受电弓模型在单、多点随机振动激励下的加速度功率谱密度响应,响应谱频率均在15 ～ 25 Hz频段时最强烈,且在多点随机振动的激励下,结构振动更为复杂,在17.48、22.53 Hz频率点附近响应更加强烈。

(2) 对比关键焊缝应力最大点的随机振动疲劳累计损伤比,车体振动对疲劳累计损伤造成影响可占总损伤的8.6%,表明弓头关键焊缝的疲劳损伤虽主要来自弓网间的高频振动,但车体振动的影响也不可忽略。

(3) 基于车辆弓网双耦合的随机振动疲劳评价方法对比传统的准静态疲劳评价方法,评估结果更为保守,具有一定的实用价值。

(4) 本文虽综合考虑了车体与弓网共同作用对受电弓疲劳强度的影响,但恶劣线路条件对强度影响的分析依据不足,其中车体激励谱选择标准谱,虽有很好的普适性,但对恶劣线路条件数据估计不足,车体振动对受电弓弓头疲劳寿命的影响程度可能由于线路条件的恶化而改变。