航态对大型船舶甲板气流场的影响

温岩殊，董文才

海军工程大学舰船工程系，湖北武汉430033

0 引 言

在大型船舶甲板气流场研究中，目前的重点主要放在船舶水上部分的空气阻力计算以及船体表面的压力场、速度场的模拟，如甲板气流场的数值模拟方法［1］，不同航速、不同海况下甲板压力场分布云图［2］、速度分布矢量图［3］，甲板气流场中尾流场的模拟［4］，甲板气流场对舰载机起降的影响［5］等，这些研究对分析大型船舶气流场的微观结构［6-8］发挥了重要作用，但是缺乏宏观的总量分析及对甲板上舰载机起降作业的研究。因此，本文拟通过对甲板气流场的分析，提出基于涡量及涡量离散度的气流场分析法。

1 计算模型与工况

1.1 数学模型

1.1.1 控制方程

本文以纳维—斯托克斯方程（Navier-Stokes方程）［9-10］作为求解不可压缩牛顿流体运动的控制方程，其形式如下：

式中：ρ 为流体密度；Fbx，Fby，Fbz分别为单位质量流体上的质量力在x，y，z 等3 个方向上的分量；u,v，w 为3 个方向上的速度分量；pij为流体内应力张量的分量；t为时间。

质量守恒方程：

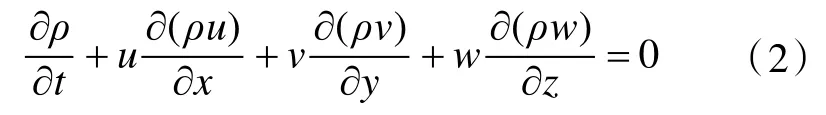
1.1.2 湍流模型

一般湍流模型有3 种：RNG k-ε，SST k-ω和Spalart-Allmaras（SA）模型，计算主要使用RNG k-ε 模型。其方程形式分别如下：

1）RNG k-ε 湍流模型。

湍流脉动动能方程（k 方程）：

湍流能量耗散率方程（ε 方程）：

式中：ui为速度分量；σx为切向应力；µ为流体粘性系数；湍动粘性系数湍动生成项Pk=µtS2，其 中，平均应变张量； σε=1.39，Cε1= 1.42，Cε2=1.68，Cµ=0.084 5，η0=4.38，β=0.012。

2）SST k-ω 湍流模型。

式中：Γκ和Γω分别表示κ 和ω 的有效扩散率；Gκ表示由于平均速度梯度产生的湍流动能；Gω表示特殊湍流动能耗散ω 的产生；Yκ和Yω分别表示由于湍流κ 和ω 的耗散；Sκ和Sω为用户自定义源项。

3）SA 湍流模型。

式中：Gυ为湍流粘性产生项；Yυ为由于壁面阻挡与粘性阻尼引起的湍流粘性的减少；συ和Cb2为常数；υ 为分子运动粘性系数。

1.2 几何模型

以排水量约60 000 t 的大型船舶为模型，使用CATIA 建立模型，船长300 m，飞行甲板中部宽约50 m。网格划分采用ICEM，计算域前后边界距离船舯分别为300 m 和-500 m，如图1 和图2所示。

图1 几何模型Fig.1 Geometry model

图2 计算网格Fig.2 Computational mesh

1.3 边界条件

计算边界条件设置如下：

1）入流边界条件定义为速度入口；

2）出流边界条件定义为速度出口；

3）模型表面定义为无滑移的壁面条件；

4）水面定义为无滑移的壁面条件。

1.4 计算工况

大型船舶实际航行时气流场情况较为复杂，本文简化了计算工况，即大型船舶在无风条件下直航，无其他干扰因素。

因大型船舶甲板为不对称结构，所以分别考虑大型船舶以20 kn 速度直航左倾、右倾及正浮情况，如表1 所示。

表1 计算工况Tab.1 Calculating cases

2 气流场横截面涡通量的定义与计算方法

2.1 横截面涡通量定义与计算

为了更好地描述大型船舶飞行甲板气流场，本文引入了截面涡通量。

式中：Ω 为涡量，n 为单位向量。横截面坐标如图3 所示，以水线处为y 轴，竖直方向为z轴。积分区域为以坐标原点为圆心，3R 为半径的半圆形区域。其中，R 为如图所示矩形对角线长，d1为上层建筑最高点距水线面距离，d2为船舶半宽。

图3 横截面坐标示意图Fig.3 Cross section coordinate system

将积分区域划分为一定数量的面积微元dydz，如图3 所示，在每个面积微元内可认为各点在各方向速度不变。求解式（8）积分，即为求解所有微元面积涡量Ωi的和。

式中：Ai为微元面积；涡量Ω 为速度场的旋度，计算公式为

可化为

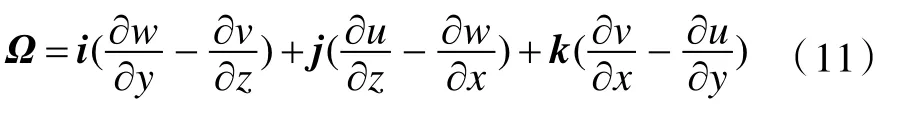
式中：u 为计算点x 方向的速度；v 为计算点y 方向速度；w 为计算点z 方向速度。涡量由速度场产生，本文仅考虑截面涡量，即忽略x 方向速度（船长方向）的影响，只计算截面上各点y，z 方向分速度对截面坐标原点O 的涡量。但是由于壁面效应的影响，在距离甲板及上层建筑表面的一小段距离内x 方向速度会逐渐降低至零。因此式（11）可简化为

由于壁面效应对整体流场涡量影响较小，在粗略计算中也可以忽略其影响，则式（12）可进一步简化为

涡量大小取模进行比较，即

在实际计算中，无法使面积微元趋于零，所以可将积分区域化为有限个面积单元，如图3 所示。靠近船体表面时面积微元可以取密集一些，远离船体表面处则可适当稀疏。本文在每个截面上选取5 000～6 000 个左右的面积微元，以面积微元几何中心处点的速度作为面积微元的总体速度，根据式（12）（或式（13））、式（14）即可得到各个面积微元的涡量Ω1，Ω2，Ω3等，然后代入式（9），即可得截面涡通量I。

本文采用CFD Post 软件取各面积微元中心点并计算各点在3 个方向上的分速度，然后代入公式求解。

为便于计算整理，将涡通量做无因次处理，定义I0为涡通量系数：

式中，取t=1 s。

2.2 截面选取和坐标系建立

建立坐标系，两坐标轴位于船纵剖面内，以船艏前125 m 处为原点，指向船艉方向为正向，如图4 所示。

计算共选取8个截面，作为甲板气流场横截面。如图4坐标系所示，从原点开始，则所选横截面纵坐标分别为0，100，200，300，400，450，525和575 m。

图4 计算坐标系Fig.4 Computational coordinate system

3 不同工况下的气流场横截面涡量计算

3.1 截面涡量分析

图5 所示为各工况截面涡通量变化曲线。图6～图10 为各工况的气流场截面流线图，图中直观呈现了各截面流场的情况。

可以看出，工况1 的曲线变化较为圆滑，从船艏甲板前端开始涡量迅速上升，至船舯部略偏后处气流场涡量值达到顶峰，而后迅速回落。

工况2 的气流场涡量从甲板前端开始迅速上升，约100 m 后达到极值，然后回落，在后1/3 甲板段气流场涡量迅速上升，在靠近船艉处达到最大值，然后迅速回落，尾流涡量变化较平缓。

工况3 的涡量变化趋势与左倾时类似，依然存在两个波峰，分别出现在甲板前1/3 处和船艉附近，但涡量值却小于左倾情况，可见上层建筑倾斜方向不同对流场影响很大。

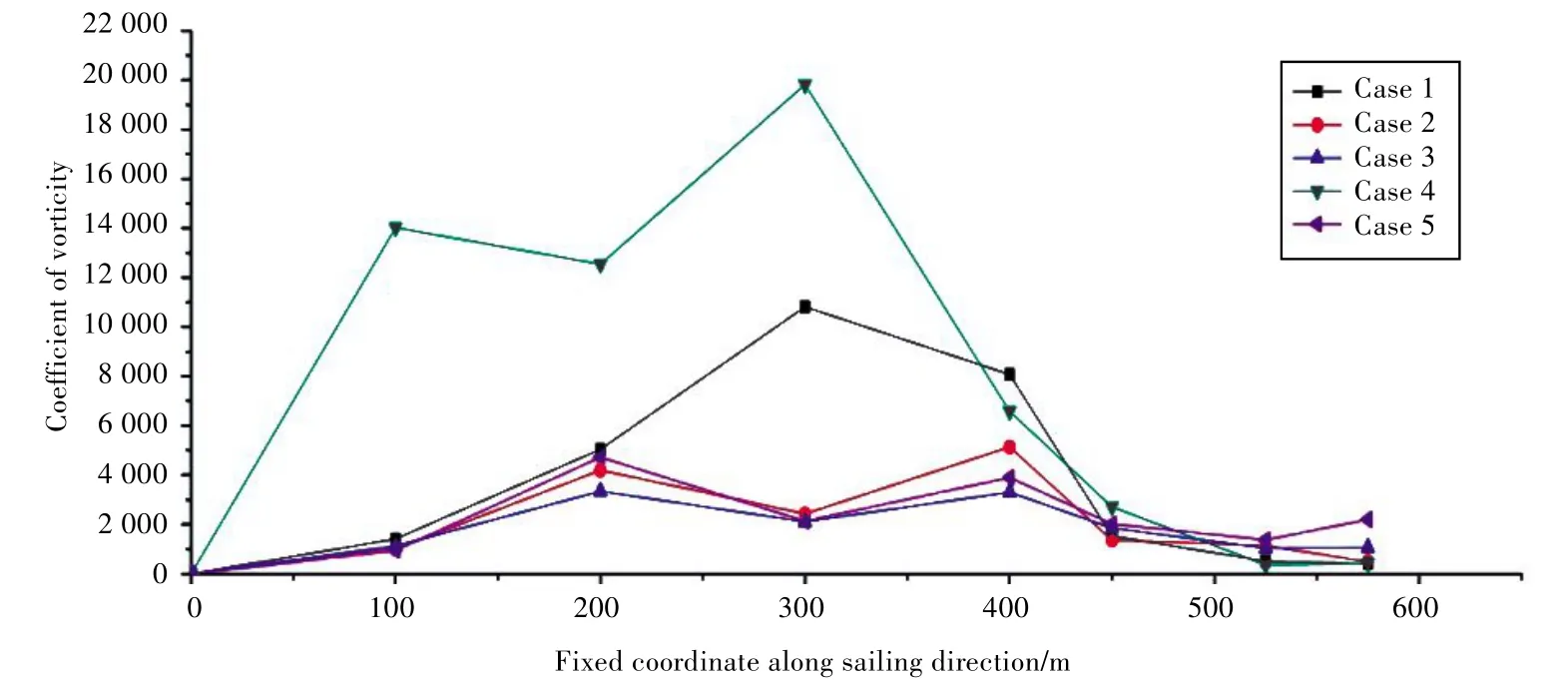
图5 各工况下横截面涡量变化曲线Fig.5 Curves of sectional vorticities for each case

图6 正浮状态横截面流线示意图Fig.6 Sectional streamlines in upright condition

图7 左倾1.5°横截面流线示意图Fig.7 Sectional streamlines in 1.5°left heel condition

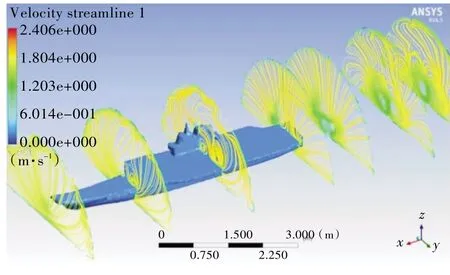
图8 右倾1.5°横截面流线示意图Fig.8 Sectional streamlines in 1.5°right heel condition

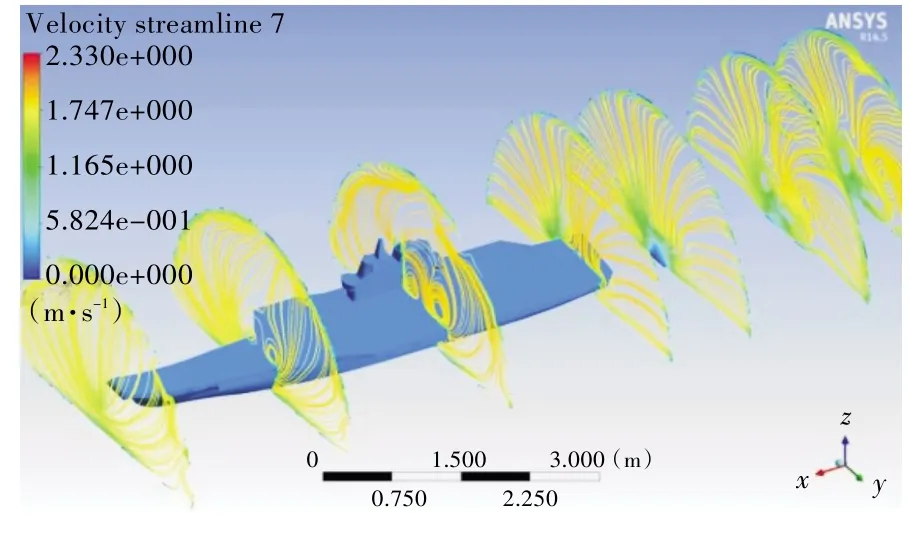
图9 左倾3°横截面流线示意图Fig.9 Sectional streamlines in 3°left heel condition

图10 右倾3°横截面流线示意图Fig.10 Sectional streamlines in 3°right heel condition

工况4 的涡量曲线出现了两次较为平缓的波峰，第一次在船艏处，而后缓慢回落，之后受上层建筑的影响气流场涡量再次上升，约在2/3 甲板处达到最大值，然后涡量开始回落至零点附近，此段曲线比较平滑。

工况5 的曲线有明显的波动，涡量在甲板前端迅速上升，最高点出现在约1/4 甲板处，而后涡量明显回落，在船艉部又有一次上升，之后迅速回落。值得注意的是，该工况对尾流场影响较大，在船艉后150 m 左右涡量再次呈上升趋势。

船舶出现横倾时涡量呈下降趋势，在横倾角达到1.5°左右时达到最小，右倾时气流场平均涡量小于左倾时。当横倾角继续增大时，气流场涡量会迅速增大。此外，随着横倾角的增大，尾流场影响范围扩大，涡量也呈增大趋势。

表2 所示为各工况下所有截面的涡量平均值。由表2 可以看出，3°左倾时甲板气流场平均涡量最大，正浮状态次之。1.5°右倾时气流场平均涡量最小。右倾状态的平均涡量要小于左倾状态。船舶出现横倾时气流场平均涡量先减小，至横倾角1.5°左右时为平均涡量最低点，而后随着横倾角的增大平均涡量开始增大。

表2 各工况下所有截面涡量平均值Tab.2 Average values of all sectional vorticities for each floating condition

3.2 涡量离散度

引入涡量离散度的概念可以更加清晰地描述甲板气流场的涡量情况。由于本文使用面积微元计算并描述涡量，则涡量离散度可由各面积微元产生的涡量（对图3 中截面原点）的离散程度来表示，即标准差σ 。

式中，Ω0为涡量平均值。

将各个截面面积微元涡量值代入式（16）和式（17），可求得各工况下各截面面积微元涡量的标准差，进而得到各截面涡量的离散程度，即涡量离散度，如表3 所示。

在表3 所示的各工况中，甲板气流场的涡量变化均呈一定趋势，但又有各自的特点。

总体趋势：在0 坐标处，气流场尚未接触船体与甲板，涡量与涡量离散度均为0。在船艏处涡量离散度开始有所增加，甲板滑跃段结束后（x=200 m）涡量有回落趋势，之后受上层建筑的影响涡量离散度又呈上升趋势，至船艉脱离甲板后逐渐回落，逐渐趋于平缓。

不同点：正浮状态与存在横倾角时的涡量离散度趋势存在一定的差异。3°左倾时涡量离散度最高，1.5°右倾时涡量离散度最低。正浮状态涡量离散度约在船舯处最高，有横倾时离散度一般会出现2 个高点，与涡通量系数曲线类似，但又不完全吻合，可见涡量大小与离散度存在一定的联系。

正浮状态涡量离散度受上层建筑影响较小，因此在甲板中段涡量离散度变化不大，但是总体离散度较高。

在左倾状态，上层建筑对气流场的影响较大，使得甲板中段涡量离散度变化剧烈，其剧烈程度与倾角大小呈正比，应引起注意。

表3 各工况下截面面积微元涡量标准差Tab.3 Standard deviation of each sectional vorticity for each floating condition

3.3 计算结果验证

为了验证本文计算结果的准确性，与文献［11］的计算结果进行了对照。文献［11］对滑跃式甲板大型船舶气流场进行了模拟计算，分别模拟了横倾角为0°，1°，2°，3°和-1°，-2°，-3°时船舶直行、风速略大于25 kn 时的甲板气流场，其计算模型、计算工况与本文接近，其气流场形态也应与本文结果接近，因此作为对照可以从侧面验证本文结果。图11 和图12 分别为左倾3°时的结果对比（舰艏方向相反），其中，图11 为本文模拟结果，图12 为文献［11］模拟结果。从图中可以看出，二者气流场形态趋势基本类似。

图11 左倾3°气流场速度云图Fig.11 Velocity contours of deck airflow field in 3°left heel condition

图12 左倾3°气流场速度云图（对照）［11］Fig.12 Velocity contours of deck airflow field in 3°left heel condition（in contrast with Fig.11）［11］

4 结 论

通过对大型船舶甲板气流场涡量及涡量离散度的分析，得出如下主要结论：

1）上层建筑会对流场产生较大影响，且左倾状态时上层建筑对气流场的影响最大，所以大型船舶在进行各项甲板作业时需留意舰岛对气流场的作用，在舰载机出动及回收时应尽量避免左倾。

2）1.5°右倾状态下，甲板气流场的平均涡量较小，滑跃甲板段涡量变化相对平缓，涡量离散度也相对较低，说明在该状态下滑跃甲板对气流场的影响较小，但是有横倾时不利于甲板人员作业，所以应尽量保持大型船舶正浮，必要时可允许一定程度的右倾。

3）无论何种工况，大型船舶尾部气流场涡量的大小和离散度都存在较大的波动，舰载机在回收时应对尾部流场的影响有足够的重视。

4）甲板气流场涡量的大小与离散度之间并无明确的对应关系，二者之间的相互影响需进一步探讨。

［1］王伟.大型舰船流场的数值计算［D］.哈尔滨：哈尔滨工程大学，2010.

［2］吕红.舰船周围气流场数值模拟方法及分布规律的研究［D］.哈尔滨：哈尔滨工程大学，2008.

［3］孙晓羽.舰船运动下舰载机阻拦着舰动力学分析与仿真［D］.哈尔滨：哈尔滨工程大学，2012.

［4］安军.航母尾流模拟及舰载机着舰控制的初步研究［D］.武汉：华中科技大学，2012.

［5］黄胜，孟祥印，常欣.航母舰载机降落制动滑跑距离分析及预报［J］.中国舰船研究，2009，4（2）：11-14.HUANG Sheng，MENG Xiangyin，CHANG Xin. Pre⁃diction and analysis on sliding distance of carri⁃er-borne aircraft landing［J］. Chinese Journal of Ship Research，2009，4（2）：11-14.

［6］徐凯.航母舰载机与偏流板的适配性研究［D］. 哈尔滨：哈尔滨工程大学，2010.

［7］宋剑，何建中.航空母舰在随机海况下的运动统计特性［J］.舰船电子工程，2011，31（3）：67-69.SONG Jian，HE Jianzhong. Statistical properties of the movement of aircraft carrier in the random sea condi⁃tions［J］.Ship Electronic Engineering，2011，31（3）：67-69.

［8］段萍萍.舰载飞机着舰性能动力学性能分析［D］. 南京：南京航空航天大学，2011.

［9］International Towing Tank Conference. Maneuvering committee final report and recommendations to the 24th ITTC［C］//Proceedings of 24th International Tow⁃ing Tank Conference.Edinburgh，UK，2005.

［10］International Towing Tank Conference. Maneuvering committee final report and recommendations to the 25th ITTC［C］//Proceedings of 25th International Tow⁃ing Tank Conference.Fukuoka，Japan，2008：14-20.

［11］王祎.载机舰在风、浪中的气流场数值模拟研究［D］.哈尔滨：哈尔滨工程大学，2010.