不规则波中船舶参数横摇的概率分析
张晓,杨和振
1 海洋工程国家重点实验室,上海200240
2 上海交通大学船舶海洋与建筑工程学院,上海200240
0 引 言
在动力系统中,随时间变化的参数会导致参量不稳定问题发生[1]。当船舶在波浪中迎浪运动时,经过船体中剖面的波高会随时间变化,从而导致船舶水线面面积随着时间不断变化,船舶初稳性高也随之变化,这种时变的初稳性高使得船舶处于参量不稳定区域,激励船舶发生大角度横摇,也即所说的船舶参数横摇。
为了获得较大的装载空间,运输汽车货车专用船、滚装船[2]和集装箱船[3]通常具有较大的艏艉外飘,其型线使得船舶在波浪中的时变初稳性高变化更为剧烈,从而使船舶更易发生参数横摇。近年来的一些集装箱船事故均与船舶参数横摇有关。1998年,由高雄开往西雅图的一艘巴拿马型集装箱船发生了30°的大角度横摇,致使集装箱落水并受损[3];而另一艘集装箱船在经历了大角度横摇后,同样遭遇了集装箱的丢失和破坏[4]。在这两起事故中,大角度横摇主要与船舶在恶劣海况下的参数横摇有关[3-4]。
在实际航行过程中,船舶的时变稳性高是随波浪而随机变化的,此时的船舶参数横摇是一个非线性的随机过程。张寿桂[5]对发生大倾角横摇时的稳性力臂予以了研究。虽然随机波浪中的船舶参数横摇已由实验证实[3,6-7],但其机理和特征还有待进一步的探讨。本文将从概率的角度研究不规则波中迎浪船舶的参数横摇,利用横摇角频率分布直方图描述时域横摇角的分布,并通过横摇角的分布情况来评估船舶航行的危险程度。为了探讨运动方程初值对横摇运动的影响,拟计算200 组数值以模拟不同时刻的横摇角标准差。
1 方法介绍
1.1 运动方程
船舶参数横摇的早期研究是基于马修方程[8-9]。随着研究的进展,为了进一步探讨参数横摇的特性,引入了阻尼项和非线性回复力矩。Yang 等[10]利用Hill 方程研究了不规则波中立管的参量不稳定性问题。本文以一艘巴拿马型集装箱船为例,采用具有线性阻尼、非线性阻尼和非线性回复力矩的横摇运动方程,利用概率统计的方法,对不规则波中船舶参数横摇进行了探讨。
不规则波中的船舶参数横摇运动可以采用下述运动方程描述:

式中:ix为船舶横摇惯性矩和附加质量;d1为船舶横摇线性阻尼;d2为船舶横摇非线性阻尼;GMb为静水初稳性高;k3为非线性回复力矩系数;φ 为船舶横摇运动横摇角;η(t)为随机波浪作用下初稳性高的波动项。规则波中初稳性高的波动是按照正弦函数的规律变化,不规则波中初稳性高的波动是一个时间的函数,形式更复杂。对于运动方程的求解,本文采用变步长Runge-Kutta法,在求解运动方程并得到横摇运动横摇角的基础上,对船舶运动的横摇角进行概率分析。
1.2 Grim 有效波理论
本文通过Bretchneider 波谱产生不规则波,Bretchneider 波谱以有义波高和谱峰周期为输入参数。Bretchneider波谱的公式如下:

式中:HS为船舶的有义波高;ωm为谱峰周期;ω为不规则波浪频率。
在所产生的不规则波谱的基础上,本文通过Grim 有效波理论对不规则波进行了简化处理。Grim 有效波理论由Grim 于1961年提出,该方法是使用与船长同长度的单波来表示通过船体的不规则波。从工程的角度看,Grim 有效波理论是一种合理的简化方法,并且已经应用于船舶参数横摇的相关研究[11]。
1.3 概率分析方法
图1 描述了船舶在不规则波中参数横摇运动横摇角的时域变化。不同的横摇角时域图因其非线性和随机性而有着显著的差别,其时域图复杂又没有规律,为了使分析更简明,更好地表示横摇角的分布规律,评估船舶运动的危险程度,采用了横摇角频率分布直方图,如图2 所示。其通过统计各个角度范围出现的频率来评估船舶在运动过程中的危险程度,和横摇角时域运动图相比,频率分布直方图更为简洁地描述了船舶在运动过程中横摇角的变化与分布情况。
为了分析不同运动方程初值的影响,对200组模拟了不同时刻的横摇角标准差进行了计算。标准差是离均差平方和平均后的方根,反映了数据集的离散程度。标准差可由如下公式计算:

图1 不规则波中横摇角随时间变化的曲线Fig.1 Roll angles in irregular wave at different time

图2 不规则波中横摇角频率分布直方图Fig.2 Histogram of frequency distribution for roll angles in irregular wave

式中:N 为样本容量;xi为样本数据;u 为样本均值。
关于标准差在不规则波参数横摇分析中的应用,将在第2.2 节具体阐述。
2 算例分析
本文以一艘巴拿马型集装箱船为例,对其在波浪中运动时的参数横摇进行了分析,该船的主尺度如表1所示。

表1 集装箱船主尺度Tab.1 Main dimensions of the container ship
2.1 规则波中船舶参数横摇
假设规则波中的船舶初稳性高按照正弦形式变化。图3 所示为规则波中横摇角φ 随时间变化的曲线。从中可以看出,当t>300 s 后,运动趋于稳定,而在此之前,横摇角的变化可以认为是从初值到稳定运动的过渡阶段。图4 所示为规则波中横摇幅值的包络线。规则波中的参数横摇可以用数值进行模拟,横摇角是从运动方程给定初值,经过过渡阶段而到达稳定值,稳定值达25 °。在数值模拟过程中,确实存在着由参数激励而导致的大角度横摇。

图3 规则波中横摇角随时间变化的曲线Fig.3 Rroll angles in regular wave at different time

图4 规则波中横摇幅值包络线Fig.4 Envelope of roll angle amplitudes in regular wave
2.2 不规则波中船舶参数横摇
图5~图7 所示分别为不规则波下初始横摇角速度为0,5,10(°)/s 时,横摇角随时间变化的曲线。对比图5 ~图7 可以看出,运动方程的初值不同,得到的时域横摇角曲线也不同。从数值模拟的角度研究船舶参数横摇,发现不同的初值会导致不同的运动特征。对于不规则波中的船舶参数横摇,本文将从概率的角度进行统计分析。

图5 初始横摇角速度为0(°)/s时不规则波中横摇角随时间变化的曲线Fig.5 Roll angles in irregular wave at different time(initial angular velocity of motion equation is 0(°)/s)

图6 初始横摇角速度为5(°)/s 时不规则波中横摇角随时间变化的曲线Fig.6 Roll angles in irregular wave at different time(initial angular velocity of motion equation is 5(°)/s)

图7 初始横摇角速度为10(°)/s时不规则波中横摇角随时间变化的曲线Fig.7 Roll angles in irregular wave at different time(initial angular velocity of motion equation is 10(°)/s)
绘制不规则波下的横摇角频率分布直方图,以探讨在不同初值下横摇角的概率分布有否不同。图8~图10 所示分别为不规则波下初始横摇角速度为0,5,10(°)/s 时,横摇角的频率分布直方图。可以通过概率分布直方图中不同横摇角出现的概率大小来评估船舶航行的危险程度。从图中可以发现,初值不同,不规则波中横摇角的频率分布直方图也有所不同。

图8 初始横摇角速度为0(°)/s 不规则波中横摇角频率分布直方图Fig.8 Histogram of frequency distribution for roll angles in irregular wave(initial angular velocity of motion equation is 0(°)/s)

图9 初始横摇角速度为5(°)/s不规则波中横摇角频率分布直方图Fig.9 Histogram of frequency distribution for roll angles in irregular wave(initial angular velocity of motion equation is 5(°)/s)

图10 初始横摇角速度为10(°)/s 时不规则波中横摇角频率分布直方图Fig.10 Histogram of frequency distribution for roll angles in irregular wave(initial angular velocity of motion equation is 10(°)/s)
船舶在实际航行时与数值模拟不同,数值模拟需要给出运动方程的初始角和初始横摇角速度,而初值的不同会造成横摇运动不同,继而得到的横摇角频率分布直方图也不同。为了忽略运动方程初值的影响,在进行概率分析时,不能采用初始时间段的横摇角数据,合适的初始时间段可以根据初值的不同予以选取。
每个初值选取200 组数值进行模拟,每组模拟5 000 s,计算每一时刻横摇角的标准差。图11~图13 所示分别为初始横摇角速度为0,5,10(°)/s 时不同时刻的横摇角标准差。
由图11~图13 可以看出,初值不同,横摇角标准差随时间变化的趋势也不同,但经过一段时间后,相对于开始时间段,横摇角标准差要更加稳定。当初始横摇角速度为0(°)/s 时,在时间t>3 000 s 之后,横摇角标准差趋于稳定,因此可以采用3 000 s 之后的横摇角数据,以降低运动方程初始值对横摇角概率统计分析的影响。而当初始横摇角速度为5,10(°)/s 时,在时间t>1 000 s 之后,横摇角标准差趋于稳定,因此可以采用1 000 s之后的横摇角数据,以降低运动方程初始值对横摇角概率统计分析的影响。

图11 初始横摇角速度为0(°)/s时不同时刻的横摇角标准差Fig.11 Standard deviation of roll angles at different time(initial angular velocity of motion equation is 0(°)/s)
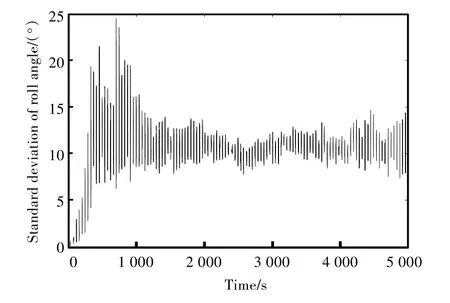
图12 初始横摇角速度为5(°)/s时不同时刻的横摇角标准差Fig.12 Standard deviation of roll angles at different time(initial angular velocity of motion equation is 5(°)/s)
3 结 论
作为船舶失稳的重要模式,探讨参数横摇对于船舶安全航行具有重要意义。本文从概率的角度探讨了不规则波中的船舶参数横摇,从以上计算和分析可以得到如下结论:
1)可以通过频率分布直方图分析不规则波中的参数横摇。和时域横摇角变化图相比,频率分布直方图更为简洁,可以通过分析不同横摇角出现的概率来评估船舶运动的危险程度。
2)运动方程的初值会影响船舶横摇运动的概率分析结果。初值不同,其时域运动不同,频率分布直方图也不同。为了排除运动方程初值对概率分析的影响,应该选取合适时间段内的横摇角数据,而合适的时间段则可以根据初值的不同来选取。
[1]杨和振,李华军. 参数激励下深海立管动力特性研究[J].振动与冲击,2009,28(9):65-69,78.YANG Hezhen,LI Huajun. Vibration analysis of deep-sea risers under parametric excitations[J]. Jour⁃nal of Vibration and Shock,2009,28(9):65-69,78.
[2]HUA J B,WANG W H.Roll motion of a roro-ship in ir⁃regular following waves[J]. Journal of Marine Science and Technology,2001,9(1):38-44.
[3]FRANCE W N,LEVADOU M,TREAKLE T W,et al.An investigation of head-sea parametric rolling and its influence on container lashing systems[J]. Marine Technology,2003,40(1):1-19.
[4]CARMEL S M. Study of parametric rolling event on a panamax container vessel[J]. Transportation Research Record:Journal of the Transportation Research Board,2006(1):56-63.
[5]张寿桂. 船舶在大风浪中横摇稳性变化的理论研究[J].中国舰船研究,2006,1(1):50-53.ZHANG Shougui. Theoretical study method for roll sta⁃bility of ships in waves[J]. Chinese Journal of Ship Research,2006,1(1):50-53.
[6]LU J,UMEDA N,MA K. Predicting parametric rolling in irregular head seas with added resistance taken into account[J]. Journal of Marine Science and Technolo⁃gy,2011,16(4):462-471.
[7]PARK D M,KIM Y,SONG K H. Sensitivity in numeri⁃cal analysis of parametric roll[J]. Ocean Engineering,2013,67:1-12.
[8]FRANCE W N,LEVADOU M,TREAKLE T W,et al. An investigation of head-sea parametric rolling and its influence on container lashing systems[J]. Marine Technology,2003,40(1):1-19.
[9]GRAFF W,HECKSCHER E. Widerstands-und stabil⁃itäts-versuche mit drei fischdampfermodellen[J].Werft-Reederei-Hafen,1941,22:115-120.
[10]YANG H Z,XIAO F,XU P J. Parametric instability prediction in a top-tensioned riser in irregular waves[J].Ocean Engineering,2013,70:39-50.
[11]HASHIMOTO H,UMEDA N. Nonlinear analysis of parametric rolling in longitudinal and quartering seas with realistic modeling of roll-restoring moment[J].Journal of Marine Science and Technology,2004,9(3):117-126.

