基于计算流体动力学的最小阻力船型自动优化
邓贤辉,方昭昭,赵丙乾
1 海军驻上海江南造船(集团)有限责任公司军事代表室,上海201913
2 中国舰船研究设计中心,湖北武汉430064
3 中国船级社武汉规范研究所,湖北武汉430022
0 引 言
国际海事组织(IMO)于2011年7月通过了MARPOL 附则VI 有关船舶能效规则的修正案,确立了船舶能效指数(EEDI)及船舶效能管理计划(SEEMP)等新要求,并将其分阶段强制实施[1]。EEDI 等新要求的实施,必将促进海事界向节能减排、绿色环保方向发展[2-3]。优秀的船体型线设计对降低能耗来说是一项影响最深、效果最长久的基础性技术,也是船舶总体设计中的一个核心环节。
传统的船型设计通常是根据母型船型线、船模系列试验资料,按照一定的规则对型线加以修改而得到,之后加工模型进行试验验证。成本高,设计周期长,尽管如此,做出的设计方案只是满足设计技术指标的可行方案而非最优设计方案。
近年来,随着计算技术的飞速发展和计算数学理论的不断完善,计算流体动力学(CFD)得到了蓬勃发展,评估能力显著增强,逐步迈向实用化,并融入到设计过程中[4-6]。CFD 方法凭借其较高的计算精确度、相对低廉的费用就能获得比模型试验更多的流场信息,成为了船舶水动力学性能分析的重要手段之一。基于CFD 的船型优化设计是随着CFD 技术、CAD 技术以及最优化技术发展而出现的一种新的船型优化方向,突破了传统船型优化技术的局限性,实现了对目标函数的直接寻优,促使工程设计从传统经验设计模式向知识化设计模式转变。如何进一步发挥CFD 在工程设计优化中的作用,是当前CFD 技术应用研究的一个重点,目前在国内外船舶设计领域引起了广泛关注[7-15]。
本文将运用iSIGHT 优化设计平台,提出一种基于CFD 的最小船型阻力自动优化方法。优化过程中,编制船型参数化融合模块,实现船型变换与SHIPFLOW 软件输入数据间的自动连接;采用遗传算法与二次序列规划法相结合的组合方法实现从全局探索再到局部空间寻优的整个优化流程。以某双艉集装箱船为例进行船型优化分析,并将优化前后的船体兴波阻力及总阻力作比较,以验证该方法的可行性与有效性。
1 船型参数化变化方法
船型的自动生成及变化是优化的基础。进行船型优化设计,首先要选择一种灵活有效且简便易行的方法来描述和修改船体的几何形状,尽量以较少的设计变量控制船型的生成,为阻力等分析提供数学模型。目前,常用的船型变换方法有数学函数法、叠加扰动面法、母型融合法等。本文将组合使用母型融合法和变换函数,实现船体曲面的局部修改及全局修改。
1.1 母型融合法
本文采用NURBS 曲线(Non-Uniform Rational B-Splines)对船型进行描述。船体曲面的融合过程实际上就是以现有的多条母型船为基础,通过融合系数(权重因子)的调节,产生一系列光顺的船型。而这一融合的过程则是直接操纵母型船NURBS 控制顶点,再由合成后的控制顶点产生船体曲面。融合过程中,保证融合系数(权重因子)的总和为1,即

式中:n 代表母型船的数量;P 代表新船的控制点坐标;Pi代表母型船的控制点坐标;Ci代表融合系数,融合过程中Ci满足

从式(2)可以看出,因融合系数的总和为1,因此无论如何调节Ci的值,融合后生成的船型均是在以母型船为边界所构成的船型空间内。如果母型船的船型特征各不相同,那么经融合后生成的线型也必然是多样的。典型的船型融合变换例子如图1 所示。

图1 基于母型船的船艏融合变化实例Fig.1 The example for bow transformation based on morphing method
1.2 变换函数法
对于常规船型,记初始母型船的船体曲面方程表示为

式中,x,y,z为NURBS控制顶点的坐标。
参数化船型变化以母型船体曲面为基础,通过构造坐标变换函数,对母型控制顶点的3 个方向坐标进行函数变换来生成新的船型。构造变换后的船型曲面方程如下:

式中:ϕ(x,y),ψ(x,y),λ(x,y) 分别为控制顶点在X 轴、Y 轴、Z 轴方向上的坐标变换函数。当这3 个函数有任何一个不为0 时,就可以产生与母型不同的船型。构造的变换函数ϕ(x,y),ψ(x,y),λ(x,y)如下:

式中:dxf,dxa分别为控制顶点X 轴方向舯前段和舯后段变换的系数;dy,dz 分别为沿船宽方向和型深方向的变化系数;ep 为型深方向变化系数,Lmax,Bmax,D 分别为最大船长、最大船宽和型深。利用该变换函数对母型船NURBS 控制顶点坐标进行修改,通过调整dxf,dxa,dy,dz,ep 的取值,即可实现母型船的参数变换。基于变换函数法的船体横剖线变化实例如图2 所示。

图2 基于变换函数法的船体横剖线变化实例Fig.2 The example for body plans optimation based on transformation function method
母型融合法的优点在于可实现船体曲面的局部修改,缺点是不容易实现船体曲面的全局修改;变换函数法的优点在于可实现船体曲面的全局修改,但曲面局部修改能力很弱。因此,本文将组合使用这两种不同的船型曲面修改方法,充分利用母型融合法及变换函数法的优点,实现船体曲面的局部及全局的修改。
2 基于CFD 的阻力数值计算
目前,基于势流理论的兴波阻力和绕船体波形的CFD 计算在实际优化设计领域中应用较多,同时粘性流计算成为CFD 计算的热点。本文从减小船体兴波阻力与总阻力的角度出发,对船体型线进行优化,采用SHIPFLOW 软件模拟计算船体阻力性能,即基于势流方法计算兴波阻力,基于粘性流方法计算粘性阻力。
运用SHIPFLOW 软件进行阻力预报时,对应不同的阻力成分,理论模型和计算原理各不相同。如图3 所示,该软件将流场划分为3 个区域:势流区、边界层区、粘性流区。其中,势流区域覆盖整个船体及周围流场的自由面,应用Rankine 源的势流方法计算船体兴波阻力;薄边界层区域采用动量积分的边界层方程计算摩擦阻力;尾部粘性区域包括船体的后部以延伸到船体下游半个船长的流体区域,采用k-ε 方程模型求解RANS 方程,计算摩擦阻力和粘压阻力等。相比全流域求解RANS 方程,采用区域划分可大幅提高计算效率,缩短计算时间。通过计算,可得到3 种类型的阻力成分:即兴波阻力、摩擦阻力和粘压阻力。上述3 种阻力构成总阻力,即兴波阻力与粘性阻力之和。图4 为某双艉集装箱船船模总阻力系数SHIPFLOW 的计算结果和水池试验结果在不同航速下的对比,试验在武汉理工大学拖曳水池进行。可以看出,不同航速下的阻力计算均与试验结果吻合良好,最大误差不超过3%。说明本文所采用的阻力数值计算方法精度较高。

图3 SHIPFLOW 中计算流场区域的划分Fig.3 Division of the zones in SHIPFLOW

图4 某集装箱船船模总阻力计算结果与试验数据比较Fig.4 Comparison of computational results with experimental data for a container ship model
3 船型优化实现过程
3.1 数学模型
1)最小兴波阻力。
优化过程中,第一步优化船艏型线。以兴波阻力Rw为目标函数:

式中:V 为航速;S 为船体湿表面积;ρ 为流体密度;Cw为兴波阻力系数,通过CFD软件SHIPFLOW计算求解。
优化目标为设计航速下兴波阻力最小,即

变量:融合系数Ci。
满足约束条件:

且艉部型线不变。
式中:Lcbbasis为母型船的浮心纵向位置;Lcbopti为优化后船的浮心纵向位置;Disbasis为母型船的排水量;Disopti为优化后船的排水量;Sbasis为母型船的湿表面积;Sopti为优化后船的湿表面积。
2)最小总阻力。
第二步,优化船艉型线。在第一步优化船型的基础上,以总阻力Rt为目标函数,即优化目标为设计航速下的总阻力最小。
目标函数:Min Rt。
变量:融合系数Ci。
约束条件:满足式(10)~式(12),且保持第一步优化后的船艏型线不变。
3.2 优化算法
文中采用混合算法,即结合遗传算法(GA)与序列二次规划法(NLPQL)。首先采用遗传算法进行初始设计空间的探索,找到近似最优解,然后利用序列二次规划法进行局部搜索,这种混合算法在改善收敛速度的同时也改进了优化结果。具体做法是在遗传算法的进化过程中,根据目标函数的进化情况自适应地判断何时停止进化,判断准则为目标函数在规定的进化代内保持不变,否则停止进化。进化过程中加入记忆体,存储最优解群体,把最优解群作为NLPQL 的初始解,然后进行NLPQL 的优化过程,算法流程如图5 所示。

图5 混合优化算法的计算流程Fig.5 Flowchart of the hybrid optimization algorithm
3.3 自动优化流程
船型阻力性能的自动优化流程如图6 所示。

图6 阻力性能自动优化流程Fig.6 Flowchart of automation optimization of resistance
优化流程简述如下:
1)根据船型修改融合方法,调整优化变量,实现对母型船球鼻艏型线的自动修改;
2)利用船型曲面全局修改方法,调整优化变量,对1)中修改的球鼻艏型线进行全局变换;
3)自动生成阻力计算软件SHIPFLOW 所需要的新船型数据文件,并进行静水力计算。若满足约束条件,则计算船体兴波阻力;反之,修改优化变量,返回第1)步;
4)以兴波阻力系数最小为优化目标,选择混合优化算法,进行船艏的优化;
5)若达到遗传次数,则输出优化后的船艏;反之,修改优化变量,返回第1)步。
6)以总阻力系数最小为优化目标,进行船艉型线优化,并输出优化后的船型。
基于多学科设计优化集成软件ISIGHT 的集成功能,完成了上述船型修改融合模块、阻力计算模块、优化计算模块的集成。
4 优化实例
4.1 算例描述
本文以某双艉集装箱船船模为例:第一步,对船艏线型进行优化,获得设计航速下(Fr=0.183)最小兴波阻力的船艏型线;第二步,在第一步优化船型基础上,对船艉线型进行优化,实现设计航速下的总阻力最小。依次进行船艏、船艉优化,分别考察艏部优化对兴波阻力的改善情况以及艉部优化对粘压阻力的改善情况。
母型船实船与船模的主要参数如表1 所示,船模的缩尺比为22.83,横剖面型线图如图7 所示。需要进行优化的艏部、艉部范围分别如图8和图9所示。

表1 某集装箱船的主要参数Tab.1 Principle dimensions of the container ship

图7 某集装箱船的型线图Fig.7 The body plans of the original container ship

图8 船模的艏部优化范围Fig.8 Forebody of the original container ship for optimization

图9 船模的艉部优化范围Fig.9 Aftbody of the original container ship for optimization
4.2 优化结果
4.2.1 艏部型线优化结果
表2 给出了集装箱船模艏部优化前后的船体阻力的结果与比较。

表2 艏部线型优化前后的船体阻力比较Tab.2 Comparison of the optimized results with the original ones
从表2 可以看出,艏部优化后船体的兴波阻力系数下降了9.8%,总阻力系数下降了2.3%。由于优化前后船体湿表面积变化很小,因此,近似认为阻力变化和阻力系数变化幅度是同步的。船艏特别是球鼻艏的变化对船体兴波阻力的影响较大,同时,船艏优化后,由于船侧波浪的峰谷变化更加平缓,粘性阻力也降低了。相比于兴波阻力,粘性阻力的变化幅度较小。船艏的优化使兴波阻力有所减小,减小兴波则直接减小了总阻力,改善了总阻力性能,表明船艏阻力性能的自动优化取得了成功。
艏部优化前后的自由面兴波波形图及舷侧纵切波形的比较分别如图10和图11所示,记船体兴波的玻高为η。优化前后船艏型线的比较如图12所示。
从图10 可以看出,优化后船体艏部的兴波波形数量有所减小,且波形变得更简单。从图11 可以看出,优化后船艏兴波的波谷无明显变化,但波峰有所减小,波高幅值变小,说明球鼻艏型线的优化对降低兴波阻力起到了显著的效果。从图12可以看出,球鼻艏向上、向前伸展一定距离的时候,兴波阻力能够得到很好的改善。
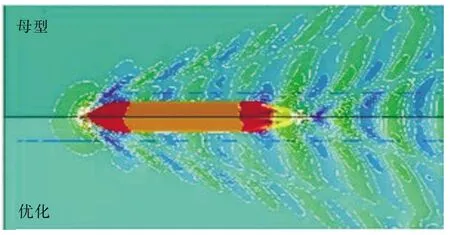
图10 艏部优化前后的船体自由表面兴波波形的比较Fig.10 Comparison of the wave contours on the free surface of the original hull with the optimized one

图11 艏部优化前后舷侧纵切波形的比较(x/L=0.1)Fig.11 Comparison of the wave height of the original hull with the optimized one at x/L=0.1
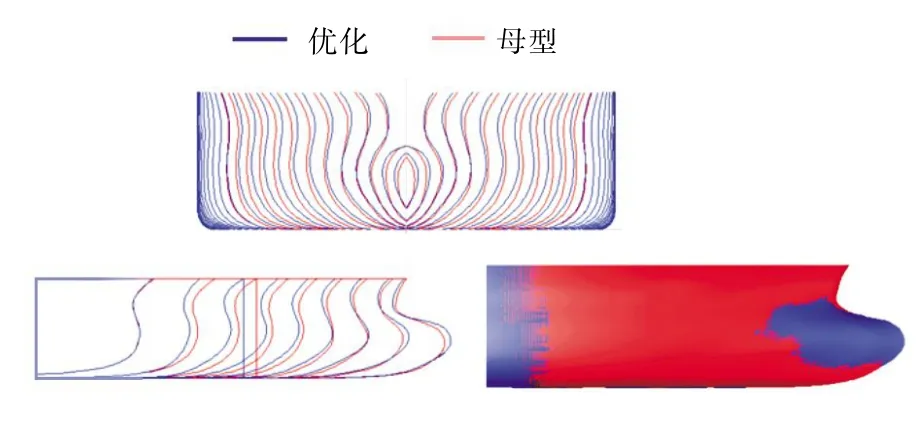
图12 优化前后的船体艏部型线的比较Fig.12 Comparison of the forebody'lines of the optimized hull form with the original one
4.2.2 艉部型线优化结果
在对集装箱船模船艏型线优化的基础上,进一步对其艉部型线进行了优化。文中根据自由面粘性流采用SHIPFLOW 软件计算船艉优化后的船体阻力。表3 给出了船艉型线优化后船体阻力与原始船模阻力结果的比较。

表3 艉部型线优化前后阻力的比较Tab.3 Comparison of the resistances of the optimized hull with the original one
从表3 可以看出,经过艏部和艉部型线两次优化后,船舶总阻力系数降低3.4%,实现了降阻的目标。图13 为优化前后艉部压力分布的比较,图14 为优化前后整船线型的比较。
从图14 艉部型线优化前后的对比可以看出,优化后船体艉部的高压区明显变大,从而导致粘压阻力的降低,进而降低了总阻力。

图13 优化前后艉部压力分布的比较Fig.13 Comparison of the pressure distribution of the optimization hull with the original one

图14 艏艉优化前后的整船型线的比较Fig.14 Comparison of the whole hull lines of the optimized hull with the original one
5 结 语
本文基于iSIGHT 优化设计平台,提出一种基于CFD 理论的最小阻力船型自动优化方法,集成了船型变换及自动生成技术、CFD 技术及优化算法。优化过程中,编制船型参数化融合模块,实现船型变换与SHIPFLOW 软件输入数据间的自动连接;采用遗传算法与二次序列规划法相结合的组合优化方法实现从全局探索再到局部空间寻优的整个流程。以某双艉集装箱船为例,进行船艏型线与船艉型线优化,优化结果显示,船体兴波阻力明显下降,总阻力也得到显著的改善,获得了设计航速下阻力最小的船艏与船艉型线组合,表明该方法可行且有效。本文所提出的方法可以获得阻力性能优良的船体型线供设计者参考,具有较强的工程适用性。在下一步的研究中,将针对优化的结果开展模型试验,以进一步验证系统优化结果的可靠性。
[1]李路,芮晓松.论EEDI(能效设计指数)的强制实施的合理性[J].中国造船,2011,52(增刊1):33-37.LI Lu,RUI Xiaosong. Comments to the compulsory im⁃plementation of EEDI [J]. Shipbuilding of China,2011,52(supp 1):33-37.
[2]谢永和,王贵彪. 拖网渔船水动力节能技术研究[J]. 水动力学研究与进展(A 辑),2014,29(2):232-237.XIE Yonghe,WANG Guibiao. Research on hydrody⁃namic energy-saving technology of the trawler[J]. Chi⁃nese Journal of Hydrodynamics(Ser. A),2014,29(2):232-237.
[3]程红蓉,陈京普,王艳霞,等. 几种船型优化手段在节能船型开发中的应用[J]. 中国造船,2012,53(增刊1):31-39.CHENG Hongrong,CHEN Jingpu,WANG Yanxia,et al. Application of several hull lines optimization meth⁃ods in green ships[J]. Shipbuilding of China,2012,53(supp 1):31-39.
[4]赵峰,李胜忠,杨磊,等.基于CFD 的船型优化设计研究进展综述[J].船舶力学,2010,14(7):812-821.ZHAO Feng,LI Shengzhong,YANG Lei,et al. An overview on the design optimization of ship hull based on CFD techniques[J]. Journal of Ship Mechanics,2010,14(7):812-821.
[5]张宝吉,马坤.基于Rankine 源法的船体线型优化设计[J]. 上海交通大学学报,2010,44(10):1414-1417.ZHANG Baoji,MA Kun. Optimization design of hull lines based on Rankine source method[J]. Journal of Shanghai JiaoTong University,2010,44(10):1414-1417.
[6]谢玲玲,冯佰威,刘祖源. 基于CFD 的高速船船体型线的自动优化[J]. 华中科技大学学报(自然科学版),2011,39(6):129-132.XIE Lingling,FENG Baiwei,LIU Zuyuan. Automatic optimization of high-speed hull forms using CFD[J].Journal of Huazhong University of Science and Tech⁃nology(Natural Science Edition),2011,39(6):129-132.
[7]陈京普,朱德祥,刘晓东.兴波阻力数值预报方法研究及其在集装箱船船型优化中的应用[J].水动力学研究与进展(A 辑),2006,12(1):113-121.CHEN Jingpu,ZHU Dexiang,LIU Xiaodong. A re⁃search on numerical prediction method for wave-mak⁃ing resistance and its application to container ship hull form optimization[J]. Journal of Hydrodynamics(Ser.A),2006,12(1):113-121.
[8]方昭昭,赵丙乾,陈庆任. 基于CFD 的双艉船型阻力数值预报[J].中国舰船研究,2014,9(4):36-62.FANG Zhaozhao,ZHAO Bingqian,CHEN Qingren.CFD theory based resistance prediction for ships with twin-skeg [J]. Chinese Journal of Ship Research,2014,9(4):36-62.
[9]徐力,陈作钢. 船体艏部水动力性能优化[J]. 中国舰船研究,2012,7(2):37-64.XU Li,CHEN Zuogang. Hydrodynamic performance optimization of ship hull's forebody[J]. Chinese Jour⁃nal of Ship Research,2012,7(2):37-64.
[10]TAHARA Y,TOHYAMA S,KATSUI T. CFD-based multi-objective optimization method for ship design[J]. International Journal for Numerical Methods in Fluids,2006,52(5):499-527.
[11]PERI D,CAMPANA E F. Multidisciplinary design optimization of a naval surface combatant[J]. Journal of Ship Research,2003,47(1):1-12.
[12]HARRIES S.Parametric design and hydrodynamic op⁃timization of ship hull forms [M]. Berlin:Mensch-und-Buch-Verlag,1998.
[13]ZHANG B J,MA K,JI Z S. The optimization of the hull form with the minimum wavemaking resistance based on Rankine Source method[J]. Journal of Hy⁃drodynamics(Ser.B),2009,21(2):277-284.
[14]钱建魁,毛筱菲,王孝义,等. 基于CFD 和响应面方法的最小阻力船型自动优化[J]. 船舶力学,2012,16(1/2):36-43.QIAN Jiankui,MAO Xiaofei,WANG xiaoyi,et al.Ship hull automated optimization of minimum resis⁃tance via CFD and RSM technique[J]. Journal of Ship Mechanics,2012,16(1/2):36-43.
[15]陈文战,陈伟,杨向晖,等.最小阻力的参数化船型优化研究[J].中国舰船研究,2013,8(2):28-33.CHEN Wenzhan,CHEN Wei,YANG Xianghui,et al. Parametric hull form optimization for minimun re⁃sistance[J]. Chinese Journal of Ship Research,2013,8(2):28-33.

