基于最大熵的新型冠状病毒代际间隔分布估计

高远东 李华龙 王小华 陈端兵 梁义娟 温涛 周涛 陶勇

摘要： 传染病代际间隔τ对于探究病毒传播规律具有重要的理论与实用价值，而通常其概率分布函数是未知的。因此，尝试利用最大熵方法推断代际间隔分布函数的最概然形式，详细分析了全球20个国家4 986个新型冠状病毒病例信息，在充分考虑样本多样性的基础上估计了该病毒代际间隔的总体均值和方差，然后基于此方法推定了全球新型冠状病毒代际间隔分布函数并以此计算了中国的基本再生数。研究结论有助于进一步客观地分析病毒传播特征，为制定常态化疫情防控对策和相关领域研究提供重要的参考价值。

关键词： 新型冠状病毒；最大熵原理；代际间隔；分布函数；阶矩信息

中图分类号： R181.8文献标识码： A

收稿日期： 2021-12-07；修回日期：2022-01-24

基金项目： 国家社会科学基金重点项目（19AJY015） ；国家自然科学基金面上项目（61673085）

第一作者： 高远东（1979-），男，内蒙古乌兰察布人，博士，教授，主要研究方向为复杂网络。

通信作者： 陶勇（1981-），男，重庆人，博士，副教授，主要研究方向为复杂系统。

Maximum Entropy Method for Estimating the Generation Interval Distribution of COVID-19

GAO Yuandong， LI Hualong， WANG Xiaohua， CHEN Duanbing， LIANG Yijuan， WEN Tao， ZHOU Tao， TAO Yong

（1.College of Economics and Management， Southwest University， Chongqing 400715， China;2. Big Data Research Center， University of Electronic Science and Technology of China， Chengdu 611731， China）

Abstract：The intergenerational τ has important theoretical and practical value to explore the law of virus transmission， but the probability distribution function is unknown. Therefore， this paper tries to infer the most probable form of the intergenerational interval distribution function  by using the maximum entropy method， and analyzes the information of 4 986 cases of novel coronavirus from 20 countries in the world in detail， and estimates the mean and variance of the intergenerational interval of the virus on the basis of fully considering the diversity of samples. Then， based on this method， the global intergenerational interval distribution function of novel coronavirus was deduced and the basic reproduction number of China is calculated. The conclusion of this study is helpful for further objective analysis of the transmission characteristics of the virus， and provides important reference value for the formulation of regular epidemic prevention and control countermeasures and related research.

Key words： COVID-19; maximum entropy method; generation interval; distribution function; moment information

0 引言

新型冠狀病毒是一种全球流行的传染病，其未知的传播动力学特征使疫情防控变得复杂。其中，代际间隔（generation interval）τ是表征流行病传播动态的关键参数之一，被定义为由上一代病例所引发的下一代病例出现的时间间隔，这需要通过调查感染者和继发感染者症状出现的日期来获取［1］。从任何个体和群体角度来看，病毒传播的信息总是有缺失和不准确的［2］。实际上，很难统计一个个体感染另一个个体的时间，所以通常用序列间隔（serial interval）对代际间隔进行近似，本文也使用序列间隔进行近似。已有的研究主要使用传统的传染病模型来分析和预测疫情的发展，而代际间隔τ又是目前主流传染病模型Susceptible-Infectious-Recovered （SIR）的重要参数［3］。

dStdt=－StNRtτIt（1）

dItdt=StNRtτIt－Itτ（2）

dH（t）dt=I（t）τ（3）

其中，Rt为新型冠状病毒在t时刻的再生数。St、It和Ht分别为t时刻社会中易感染者、感染者和康复者的个体数目。令全社会的总人数为N，则有

N=St+It+Ht（4）

对于一次传染病疫情，模拟疫情的演化趋勢需要掌握传染病模型中的基本再生数R0，而基本再生数R0的计算需要知道代际间隔τ的概率分布函数p（τ）。如何从有限的疫情观测数据去推测背后潜藏的普遍性法则，拟合相关的已知事实来准确估计代际间隔τ的概率分布函数p（τ），对于掌握新冠疫情的流行病学特征，进行疫情防控以及相关领域的研究至关重要。

新冠疫情暴发以来，对新型冠状病毒的研究也呈爆发式增长，学者们在估计流行病学参数、疫情数据挖掘、疫情实时预测等方面展开了大量研究［2］。部分研究使用蒙特卡洛模拟［4］与贝叶斯估计［5］进行代际间隔分布p（τ）的后验推断，但在实际的应用中，代际间隔的估计需要尽可能完备的病例信息。由于总体信息缺乏，使得推断结果依赖于样本量的大小。在现实世界中，真实病毒传播过程十分复杂，特别是在疫情早期传播中，超级传播事件使得继发感染数庞杂［6］。与其他传染病一样，新型冠状病毒流行病学参数估计通常面临着数据质量和可用性问题以及数据详实程度与覆盖范围间的权衡。面对这样的困难，早期的估计借鉴了SARS的参数［78］，最近的估计利用了新型冠状病毒早期病例的信息［910］，而且人们往往事先假定概率分布函数p（τ）为正态分布［911］、Weibull分布［1213］或者Gamma分布［8，1417］等，还没有一个原理性的方案来确定概率分布。这样先验地假定代际间隔服从某种分布具有较大的主观性，并且大部分研究是一种小子样不确定分析。更重要的是，假定不同函数类型的p（τ）分布，可能为疫情防控给出不一致的参考标准，对政策制定者评估疫情的发展趋势带来极大的不确定性。

理论上，一组样本数据的分布形态特点可以用各个阶矩刻画，例如一阶矩是数据的均值，二阶矩为方差，三阶矩为偏度，四阶矩为峰度。假如有样本量为n的数据，1至n阶矩都是已知的，那么联立n个阶矩方程就可以求出n个样本的具体数值，从而获取样本的所有信息。但是，现在很大一部分国家仅公布了新型冠状病毒代际间隔τ的一阶矩（均值）与二阶矩（方差），并没有完整的样本信息。这使得蒙特卡洛模拟与贝叶斯估计等方法很难用于准确估计代际间隔分布。最大熵方法的内在优越性则在于先验假定总体信息缺失，最大效率地利用已知的样本信息对代际间隔的未知高阶矩进行非零外推，使得代际间隔的概率分布估计最概然。鉴于在不完全信息下推断概率分布的巨大优势，最大熵原理已经被广泛应用于人工智能、经济学、生态学等领域。最近，最大熵原理也被应用于传染病领域［7］，但利用最大熵方法估计新型冠状病毒COVID-19的研究还比较缺乏［2，7］。因此，本文利用收集的4 986例全球新型冠状病毒一阶矩与二阶矩样本信息，利用最大熵方法刻画了涵盖20个国家代际间隔的概率分布函数，从而最概然地还原原始代际间隔的分布。其中，在使用样本的阶矩信息时，本文通过加权统计减少组间的系统性误差，以此来近似原始总体病例的对应阶矩信息。利用该分布函数，本文估算了新型冠状病毒的基本再生数。

与既有的研究相比，本文的贡献在于：1）充分利用全球已知代际间隔信息，并在新型冠状病毒代际间隔估计中考虑了信息不完整这一要素；2）将“熵最大”作为判定依据，使得代际间隔的估计唯一给定，不再需要通过对未知部分作出先验假定，减少了主观假设；3）利用较大的样本数量刻画了全球代际间隔分布函数的最概然形式，并估计了中国基本再生数R0，对后疫情阶段具有潜在的应用价值。

1 最大熵原理下的代际间隔分布函数

最大熵原理起源于信息论和统计力学，是基于有限的已知信息对未知分布进行无偏推断的一种数学方法。最近的研究表明该原理也可以用来确定流行病学参数和传播动力学特征［7］。对于一次疫情，尽管代际间隔的分布形式p（τ）是未知的，但人们却可以测定代际间隔均值和方差，这就为最大熵原理的使用提供了基本信息来源。

2 代际间隔的估计

2.1 数据获取与处理

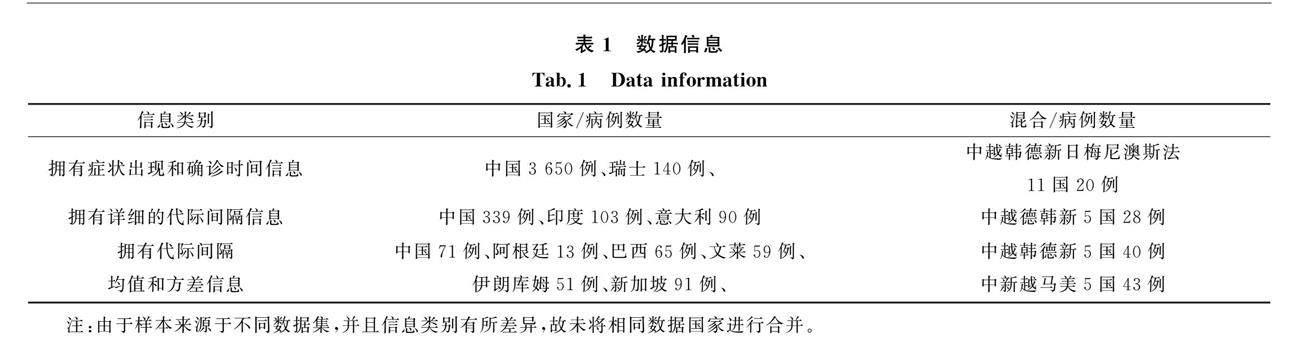
为了加大样本的地区多样性，从而更可靠地估计代际间隔的概率分布函数，本文尽可能收集了多个不同国家的代际间隔信息。在排除了部分重复率较高的数据后，最终获得了2019年12月到2020年8月期间，来自中国、美国、日本、新加坡、瑞士、越南、泰国、马来西亚、法国、巴西、阿根廷、意大利、伊朗、文莱、德国、澳大利亚、尼泊尔、斯里兰卡、韩国、印度20个国家的4 986个病例信息，具体见表1。

其中，“混合/病例数量”代表数据集包含了多个国家，细化程度低且难以剥离，因此将含有多个国家代际间隔的混合数据作为一个独立单元。采用这样的数据粒度划分策略，有效地解决了代际间隔估计中面临的数据信息多样化问题。

从表1收集的数据来看，我们能掌握的代际间隔信息有着如下特征：1）样本数量少，能够获得超过30个样本信息的国家较少，并且大部分国家只公布了均值与方差；2）覆盖的地区、包含的数量相对有限，信息不完整并且零散；3）系统性误差高，并且存在部分代际间隔为负值的情况。这些现实情况使得利用其它统计推断方法估计代际间隔分布非常困难。相比之下，最大熵方法可以将拥有的样本均值与方差的信息客观地编入特定概率分布中，来描述代际间隔的最佳近似分布。

此外，本论文对上述数据作如下处理：1）收集拥有第一代症状出现、第一代确诊时间、第二代症状出现时间的新加坡50例证据，近似仅包括精确的症状出现和确诊时间的代际间隔值；2）代际间隔是从上一代病例症状出现的日期开始计算的，这表明负值可能是由于个体之间的潜伏期长短不同造成的。借鉴文献［20］对拥有代际间隔详细信息的病例，将负值重置为零来实现简单的校正。

2.2 各样本代际间隔概率分布

由于样本信息抽取于不同的数据集，数据类型有所差异，例如中国武汉71例仅能获取代际间隔的阶矩信息，而中国3 650例则需要近似生成代际间隔信息。但在所有的样本信息中，均可获取生成间隔的均值和方差，这就为最大熵方法包容性地利用多元化的数据提供了信息基础。数据来源以及各组新型冠状病毒的代际间隔的均值和方差，参见文献［8-9］、［11］、［13］、［15-17］、［20-29］。利用式（13），求解出p（τ）的待定参数α、β和γ以及代际间隔τ的概率分布函数如表2所示。

其中，具有详细频数分布的代际间隔概率分布函数如图1～7所示。在不同地区，由于防控举措以及疫情阶段的不同，新型冠状病毒代际间隔的概率分布差异较大。

2.3 全球代际间隔概率分布

本节采用收集的样本均值与方差估计全球代际间隔概率分布。为了增强统计推断的可靠性，对全球代际间隔的均值和方差均采用样本不平等加权与平等加权分别进行计算，其计算公式分别表达为

τa=n11+n22+…+nmmn1+n2+…+nm（14）

σ2a=n1－1σ21+n2－1σ22+…+nm－1σ2mn1－1+n2－1+…+nm－1（15）

b=1+2+…+mm（16）

σ2b=σ21+σ22+…+σ2mm（17）

其中，a和σ2a充分考虑了系统性误差的不平等加权统计量，b和σ2b为平等加权统计量，n为各组的病例数量，为各组的均值，m为组数。这里需要特别注意的是，利用最大熵方法求出的代际间隔分布函数（11）是在假定总体均值和总体方差σ2已知的情况下进行的，但实际上并不能掌握总体均值与方差的精确值。

但由于本研究收集了全球20个国家4 986例大样本数据，因此可以尝试利用样本均值与方差来近似总体均值与方差。这个近似成立的前提是：构造的样本均值与方差满足一致性，各组之间的系统性误差应该非常小，使得不平等加权统计量a和σ2a与平等加权统计量b和σ2b分别近似相等。因此，本文基于最大熵方法，利用样本

均值与样本方差，分别求出α、β、γ的值（见表3）。

从代际间隔的参数来看，一方面，由4 986个病例样本计算得到的样本方差与样本均值满足一致性，a与b、σ2a与σ2b分别近似相等。另一方面，所估计的样本均值与样本方差可以较好地反映总体特征。文獻［22］中采用中国武汉6例病例时，平均代际间隔为7.5 d，而文献［8］中用中国香港21例时，平均代际间隔为4.4 d。本文采用20个国家数据近似代际间隔总体均值为5.05和5.14，一定程度上削弱了小子样不确定分析对估计分布函数造成的影响。

综上，不平等加权和平等加权代际间隔概率分布函数pu（τ）和peτ分别为

puτ=0.171 4exp［－0.116 1τ－0.015 3τ－5.052］peτ=0.166 1exp［－0.097 7τ－0.020 1τ－5.142］（18）

为了更加直观地观察代际间隔概率分布，本文利用式（18）刻画出代际间隔概率分布图如图8～9所示，并且展示了尽可能收集到的新型冠状病毒全球4 370例详细代际间隔的频数分布。其存在着如下特征：1）代际间隔概率分布函数与频数分布相吻合，证明了上述概率分布函数的可靠性；2）不平等加权和平等加权代际间隔概率分布函数pu（τ）和peτ在图中形态相似，反映了上文计算的代际间隔阶矩信息的一致性。

3 估计结果比较

3.1 代际间隔分布函数比较

从图8，图9观察到平等加权的概率分布图与真实数据拟合程度更高，本文则利用平等加权的代际间隔分布图与文献［10］，［21］，［30］中拟合的Gamma分布、正态分布和对数正态分布进行比较，进而可视化地比较分析最大熵方法相对于不同先验假设方法拟合真实数据的情况。

从图10可以直接观察到Gamma分布、正态分布和对数正态分布与本文收集的4 370例全球真实数据拟合情况。相对于最大熵方法，对数正态分布和Gamma分布未能捕捉到代际间隔在零点的信息，这很容易低估新型冠状病毒的传染性。不过，相较于最大熵方法，对数正态分布对代际间隔偏度和峰度的信息捕捉较好，而Gamma分布也捕捉到偏度的信息。这是由于在现实中所能收集的代际间隔数据缺失了峰度（四阶矩）和偏度（三阶矩）等重要的高阶矩信息，而只将均值（一阶矩）与方差（二阶矩）作为约束求解最大熵的分布函数。显然，均值与方差只提供了代际间隔分布图形的位置与宽度等信息，无法提供分布图形的偏度和峰度信息。

虽然未能进一步掌握更高阶矩的信息，但最大熵方法所估计分布函数的综合效果要优于其他分布，先验假定代际间隔服从其他函数分布，虽然也考虑了代际间隔的统计特征，但增加了不相关的信息，影响了估计的准确性。从这个意义上，利用最大熵方法估计新型冠状病毒的代际间隔具有一定优势。更重要的是，倘若能够掌握到更加完备的病例信息（比如获取到峰度和偏度的估计值），则可进一步利用最大熵方法更加准确地估计代际间隔的分布函数，这是本文的客观不足也是下一步的研究方向。

3.2 再生数R0

本节将基于最大熵方法得到的全球代际间隔概率分布用于新型冠状病毒中国基本再生数的估计。基本再生数R0的数学表达式为［7］

R0=It/∫SymboleB@0It－·peτdτ（19）

因为时间的单位是d，而我们只能收集到被感染者人数的离散值。为了通过方程（19）计算基本再生数R0，需要将积分（19）改写为求和形式。图8～9中分布函数p（τ）的分布规律暗示新型冠状病毒一个传染周期可以近似为14 d，即pτ=14≈0。这里采用14作为积分上限（与15得到结果的差值可以忽略不计），方程（19）可以被写为

R0=Rt=14≈It=14/∑14τ=0I14－·peτ（20）

利用方程（20）可以以14 d为周期计算新型冠状病毒的基本再生数R0。由于疫情传染周期为14 d，因此需要确定一个周期的起点。根据中国卫健委的数据报告（http：//www.nhc.gov.cn/），2020年1月8日是一个疫情周期的结束，我们将2020年1月9日记为周期的第一天，计算得到基本再生数R0为3.09。

此外，如表4所示，本文收集了新型冠状病毒基本再生数的相关研究，利用在较长的期间内收集的样本信息，本文所估计的基本再生数同中间值接近，并且符合现实传播情况。

4 讨论与结论

针对现有疫情样本信息的缺失，为了更加准确地估计代际间隔的最概然形式，本文提出了一种基于最大熵原理的估计方法，该方法能够尽可能充分地利用有限样本信息去挖掘数据特征。以新型冠状病毒为例，本论文特别收集了全球20个国家4 986个病例的阶矩信息，估计了全球新型冠状病毒代际间隔的概率分布函数以及中国的基本再生数，从而为揭示全球新型冠状病毒的传播规律提供统计参考。

在传播动力学参数上，本文估计的新型冠状病毒加权代际间隔均值为5.05 d，方差为13.561，与大部分文献估计的4～8 d相符［43］，相比之下，新加坡SARS的平均代际间隔估计为8.4 d，传播的代际间隔缩短了39.9%。基本再生数R0为3.09，根据文献［44］的估算，对于R0值为2.5至3.5之间，如果有40例初始病例，只有在症状出现前传播率低于1%时，才有可能追踪和隔离接触者。这些传播参数表明新型冠状病毒需要采取更为严格的防控措施、作出更大的努力来减少传播。并且现阶段应特别重视预防和控制超级传播事件，降低由单个病例迅速建立持续传播链的可能性。

在估计方法上，假如已掌握所有病例样本的信息，那么则可以通过蒙特卡洛模拟与贝叶斯估计等方法近似推断出总体的代际间隔分布。但是目前很大一部分国家只公布了新冠病毒代际间隔的一阶矩（均值）和二阶矩（方差），这使得蒙特卡洛模拟与贝叶斯估计等方法无法应用到代际间隔的分布估计。相比之下，最大熵方法既可以将样本的所有阶矩信息作为其“约束条件”解决这一适定的数学问题，也可以在只有部分阶矩已知的情况下估计总体代际间隔分布。理论上，只要样本阶矩值充分趋近于总体阶矩值（即满足统计量的一致性），那么最大熵方法就可以在已知部分样本阶矩的情况下做出总体分布的无偏估计。

本文将最大熵方法應用于新型冠状病毒代际间隔的估计，其优势一方面在于确定代际间隔分布不涉及过多的主观假定，与其他方法相比具有较好的自洽性，不存在利用过多的假设去修改样本数据的信息。另一方面，通过一阶矩（均值）和二阶矩（方差）即可给出代际间隔概率分布函数的最概然形式，充分利用疫情初期或者不同地区零散信息，尽可能客观准确地刻画新冠疫情的代际间隔，并用于再生数等流行病参数的计算，有利于为掌握该流行病的传播特征和趋势提供统计参考。

最后需要指出，代际间隔估计精确程度与其分布函数的细节还受到阶矩信息数目的影响。本文仅考虑了代际间隔样本数据均值与方差。未来可进一步结合更高阶矩的信息优化该方法还原原始数据，比如样本数据三阶矩和四阶矩信息，以进一步捕捉到代际间隔分布函数的偏度和峰度等图形特征，对流行病传播动态等问题给出更加准确的估计和预测。

参考文献：

［1］WALLINGA J， LIPSITCH M. How generation intervals shape the relationship between growth rates and reproductive numbers［J］. Proceedings of the Royal Society B-biological Sciences， 2007， 274（1609）： 599-604.

［2］杜亦牧，孙昌璞. 基于最大熵原理可靠性分析的病毒传播模型［J］. 科学通报， 2020， 65（22）： 2356-2362.

DU Y M， SUN C P. Maximum entropy approach to reliability analysis based epidemic disease model［J］. Chinese Science Bulletin， 2020， 65（22）： 2356-2362.

［3］KENAH E， ROBINS J M. Second look at the spread of epidemics on networks［J］. Physical Review E， 2007， 76 （3）： 36113-36113.

［4］WU J T， LEUNG K， LEUNG G M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan， China： a modelling study ［J］. Lancet， 2020， 395（10225）： 689-697.

［5］CAUCHEMZ S， BOELLE P Y， DONNELLY C A， et al. Real-time estimates in early detection of SARS［J］. Emerging Infectious Diseases， 2006， 12（1）： 110-113.

［6］HASAN A， SUSANTO H， KASIM M F， et al. Superspreading in early transmissions of COVID-19 in Indonesia［J］. Scientific Reports， 2020， 10 （1）： 22386.

［7］TAO Y. Maximum entropy method for estimating the reproduction number： an investigation for COVID-19 in China and the United States［J］. Physical Review E， 2020， 102（3）： 0321363.

［8］ZHAO S， GAO D， ZHUANG Z， et al. Estimating the serial interval of the novel coronavirus disease （COVID-19）： a statistical analysis using the public data in Hong Kong from January 16 to February 15， 2020［J］. Frontiers in Physics， 2020， 8（9）： 347.

［9］DU Z， XU X， WU Y， et al. COVID-19 serial interval estimates based on confirmed cases in public reports from 86 Chinese cities［DB/OL］. （2020-04-23） ［2021-11-15］. http：//www.medrxiv.org/content/10.1101/2020.04.23.20075796.

［10］ DU Z， XU X， WU Y， et al. Serial Interval of COVID-19 among publicly reported confirmed cases［J］. Emerging Infectious Diseases， 2020， 26（6）： 1341-1343.

［11］ WONG J， CHAW L， KOH W C， et al. Epidemiological investigation of the first 135 COVID-19 cases in Brunei： implications for surveillance， control， and travel restrictions［J］. American Journal of Tropical Medicine， 2020， 103（4）： 1608-1613.

［12］ LIPSITCH M， COHEN T， COOPER B， et al. Transmission dynamics and control of severe acute respiratory syndrome［J］. Science， 2003， 300 （5627）： 1966-1970.

［13］ NAJAFI F， IZADI N， Hashemi-Nazari S， et al. Serial interval and time-varying reproduction number estimation for COVID-19 in western Iran［J］. New Microbes and New Infections， 2020， 36（7）： 100715.

［14］ ZHANG S， DIAO M， YU W， et al. Estimation of the reproductive number of novel coronavirus （COVID-19） and the probable outbreak size on the Diamond Princess cruise ship： a data-driven analysis［J］. International Journal of Infectious Diseases， 2020， 93（4）： 201-204.

［15］ GANYANI T， KREMER C， CHEN D， et al. Estimating the generation interval for coronavirus disease （COVID-19） based on symptom onset data， March 2020［J］. Euro Surveillance ： Bulletin Europeen Sur Les Maladies， 2020， 25（17）： 12-19.

［16］ AGHAALI M， KOLIFARHOOD G， NIKBAKHT R， et al. Estimation of the serial interval and basic reproduction number of COVID-19 in Qom， Iran， and three other countries： a data-driven analysis in the early phase of the outbreak［J］. Transboundary and Emerging Diseases， 2020， 67（6）： 2860-2868.

［17］ WU J T， LEUNG K， BUSHMAN M， et al. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan， China［J］. Nature Medicine， 2020， 26（4）： 506-510.

［18］ ZHOU T， LIU Q， YANG Z， et al. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV［J］. Journal of Evidence-Based Dental Practice， 2020， 13（1）： 3-7.

［19］ JAYNES E T. On the rationale of maximum-entropy methods［J］. Proceedings of the IEEE， 1982， 70（9）： 939-952.

［20］ YOU C， DENG Y， Hu W， et al. Estimation of the time-varying reproduction number of COVID-19 outbreak in China［J］. International Journal of Hygiene and Environmental Health， 2020， 228（7）： 113555.

［21］ CHEN D， ZHOU T. Evaluating the effect of Chinese control measures on COVID-19 via temporal reproduction number estimation［J］. PLoS One， 2021， 16（2）： e0246715.

［22］ LI Q， GUAN X， WU P， et al. Early Transmission dynamics in Wuhan， China， of novel coronavirus-infected pneumonia［J］. New England Journal of Medicine， 2020， 382（13）： 1199-1207.

［23］ VIEGO V， GERI M， CASTIGLIA J， et al. Incubation period and serial interval of Covid-19 in a chain of infections in Bahia Blanca （Argentina） ［DB/OL］. （2020-06-18）［2021-11-15］. https ：//doi.org/10.1101/2020.06.18.20134825.

［24］ PRETE C A， BUSS L， DIGHE A， et al. Serial interval distribution of SARS-CoV-2 infection in Brazil［J］. Oxford University Press Public Health Emergency， 2021， 28（2）： 115.

［25］ SAURABH S， VERMA M K， GAUTAM V， et al. Transmission dynamics of the COVID-19 epidemic at the district level in India： prospective observational study［J］. JMIR Public Health and Surveillance， 2020， 6（4）： e22678.

［26］ CHINTALAPUDI N， BATTINENI G， SAGARO G G， et al. COVID-19 outbreak reproduction number estimations and forecasting in Marche， Italy［J］. International Journal of Infectious Diseases， 2020， 96（5）： 327-333.

［27］ JEREMIE S， SARAH N， TIMOTHY V G， et al. Reproductive number of the COVID-19 epidemic in Switzerland with a focus on the cantons of basel-stadt and basel-landschaft［J］. Schweizerische Medizinische Wochenschrift， 2020， 150（4）： w20271.

［28］ FERRTTI L， WYMANT C， KENDALL M， et al. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing［J］. Science， 2020， 368（6491）： 6936.

［29］ NISHIURA H， LINTON N M， AKMETZHANOV A R. Serial interval of novel coronavirus （COVID-19） infections［J］. International Journal of Infectious Diseases， 2020， 93（4）： 284-286.

［30］ WANG K， ZHAO S， LIAO Y， et al. Estimating the serial interval of the novel coronavirus disease （COVID） based on the public surveillance data in Shenzhen， China from January 19 to February 22， 2020［J］. Transboundary and Emerging Diseases， 2020， 67（6）： 2818-2822.

［31］ MAJUMDER M S， Mandl K D. Early transmissibility assessment of a novel coronavirus in Wuhan， China［DB/OL］. ［2021-11-15］. https：//tongtianta.site/paper/76230.

［32］ RIOU J， ALTHAUS C L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus （2019-nCoV）， December 2019 to January 2020［J］. Euro Surveillance ： Bulletin Europeen sur les Maladies， 2020， 25（4）： 7-11.

［33］ LIU Q H， BENTO A I， YANG K X， et al. The COVID-19 outbreak in Sichuan， China： epidemiology and impact of interventions［DB/OL］. （2020-07-20）［2021-11-15］. https ：//doi.org/10.1101/2020.07.20.20157602.

［34］ AHMAD Z， ARIF M， ALI F， et al. A report on COVID-19 epidemic in Pakistan using SEIR fractional model［J］. Scientific Reports， 2020， 10（12）： 22268.

［35］ WU J T， LEUNG K， LEUNG G M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan， China： a modelling study［J］. Lancet， 2020， 395（10225）： 689-697.

［36］ LIU T， HH J， KANG M， et al. Transmission dynamics of 2019 novel coronavirus （2019-nCoV） ［DB/OL］. ［2021-11-15］.http：//dx.doi.org/10.2139/ssrn.3526307.

［37］ READ J， BRIDGEN J， CUMMINGS D， et al. Novel coronavirus 2019-nCoV： early estimation of epidemiological parameters and epidemic predictions［DB/OL］. （2020-01-23）［2021-11-15］. https：//doi.org/10.1101/2020.01.23.20018549.

［38］ SHIM E， TARIQ A， CHOWELL G. Spatial variability in reproduction number and doubling time across two waves of the COVID-19 pandemic in South Korea， February to July， 2020［J］. International Journal of Infectious Diseases， 2020， 102（1）： 1-9.

［39］ CAO Z， ZHANG Q， LU X， et al. Estimating the effective reproduction number of the 2019-nCoV in China［DB/OL］. （2020-01-27）［2021-11-15］. https：//doi.org/10.1101/2020.01.27.20018952.

［40］ GUO Z， XIAO D. Analysis and prediction of the coronavirus disease epidemic in China based on an individual-based model［J］. Scientific Reports， 2020， 10（12）： 22123.

［41］ TANG B， WANG X， LI Q， et al. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions［J］. Journal of Clinical Medicine， 2020， 9（2）： 462.

［42］ SHEN M， PENG Z， XIAO Y， et al. Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China［J］. The Innovation， 2020， 1（3）： 100048.

［43］ PARK M， COOK A R， Lim J T， et al. A systematic review of COVID-19 epidemiology based on current evidence［J］. Journal of Clinical Medicine， 2020， 9（4）： 967.

［44］ HELLEWELL J， ABBOTT S， GIMMA A， et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts［J］. The Lancet Global Health， 2020， 8（4）： 488-496.

（責任编辑 耿金花）