基于一种四维忆阻超混沌系统的图像加密算法

闫少辉 顾斌贤 宋震龙 施万林

摘要： 鉴于低维混沌的图像加密算法存在密钥空间小、安全性不高等问题，通过引入光滑三次型忆阻器，构建一个改进的四维忆阻超混沌系统。对改进系统的相图、耗散性、平衡点稳定性、Lyapunov指数谱和分岔等进行数值仿真与分析，表明该系统具有丰富的动力学行为与混沌特性。并提出一种通过哈希算法进行混沌序列选择的加密算法。经过直方图、密钥空间分析、鲁棒性分析等实验仿真，表明该图像加密算法密钥空间较大，可以有效抵御暴力穷举等恶意攻击，具有较高的安全性。

关键词： 忆阻器；超混沌系统；动力学特性；图像加密；哈希算法

中图分类号： TP309.7；O415.5文献标识码： A

收稿日期： 2021-09-15；修回日期：2021-12-24

基金项目： 甘肃省自然科学基金（20JR5RA531）

第一作者： 闫少辉（1980-），女，甘肃镇原人，博士，副教授，主要研究方向为非线性电路及应用。

Image Encryption Algorithm Based on a Four-dimensional Memristor Hyperchaotic System

YAN Shaohui， GU Binxiana， SONG Zhenlonga， SHI Wanlina

（a. College of Physics and Electronic Engineering;

b. Engineering Research Center of Gansu Province for Intelligent Information Technology and Application， Northwest Normal University， Lanzhou 730070， China）

Abstract：The image encryption algorithm based on low dimensional chaotic system has the problems of the key space small and the security not high. In this paper， an improved four-dimensional Lorenz dissipative hyperchaotic system is constructed by introducing a cubic smooth memristor model. The dynamic characteristics of the improved system such as phase portraits， dissipation， equilibrium stability， Lyapunov exponent， and bifurcation are investigated， it is proved that the system has good dynamic characteristics and chaotic attractor. Therefore， a chaotic sequence encryption algorithm based on Hash algorithm is proposed. By histogram， key space analysis，robust analysis and other verifications show that the image encryption algorithm has higher key space and can resist brute-force attack.

Key words： memristor; hyperchaotic system; dynamic characteristic; image encryption; hash algorithm

0 引言

1971年，蔡少棠教授基于電路对称性理论推导出了忆阻器的存在［12］。忆阻器作为第四种基本电路元件，因具有无源以及电荷记忆特性，成为实现存储计算、仿生智能的关键器件，从而引起许多研究团队的兴趣［36］。同时它还具有非线性输入输出特性，在混沌电路中能够产生复杂的动力学行为。

1989年，Matthews R首次通过Logistic映射产生大量的伪随机数据［7］。从此，混沌系统开始与加密系统结合起来，开创了混沌系统产生伪随机数的新方法，Logistic混沌系统、Lorenz混沌系统逐渐在图像加密中得到应用［8］。

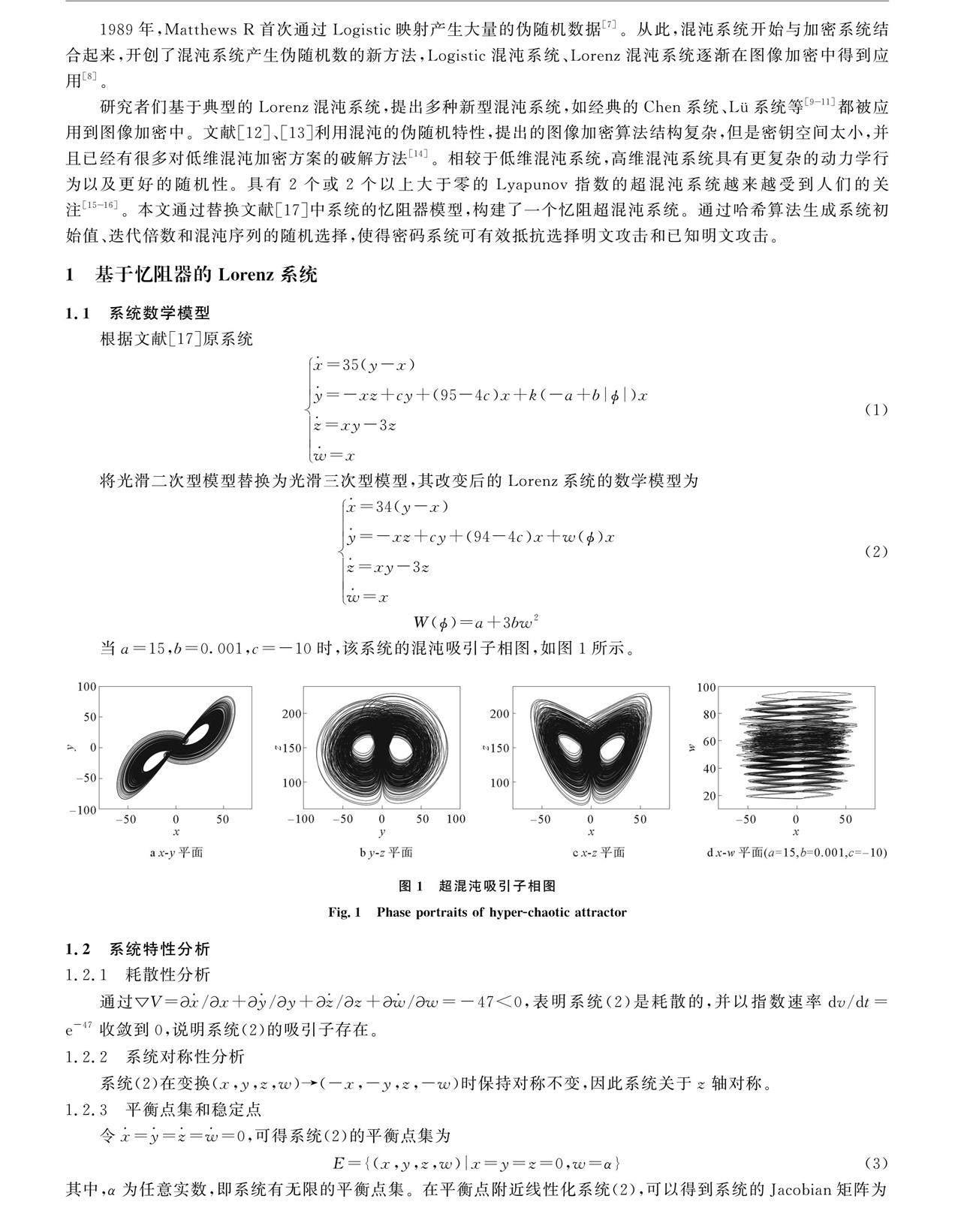
研究者们基于典型的Lorenz混沌系统，提出多种新型混沌系统，如经典的Chen系统、Lü系统等［911］都被应用到图像加密中。文献［12］、［13］利用混沌的伪随机特性，提出的图像加密算法结构复杂，但是密钥空间太小，并且已经有很多对低维混沌加密方案的破解方法［14］。相较于低维混沌系统，高维混沌系统具有更复杂的动力学行为以及更好的随机性。具有2个或2个以上大于零的Lyapunov指数的超混沌系统越来越受到人们的关注［1516］。本文通过替换文献［17］中系统的忆阻器模型，构建了一个忆阻超混沌系统。通过哈希算法生成系统初始值、迭代倍数和混沌序列的随机选择，使得密码系统可有效抵抗选择明文攻击和已知明文攻击。

5 结论

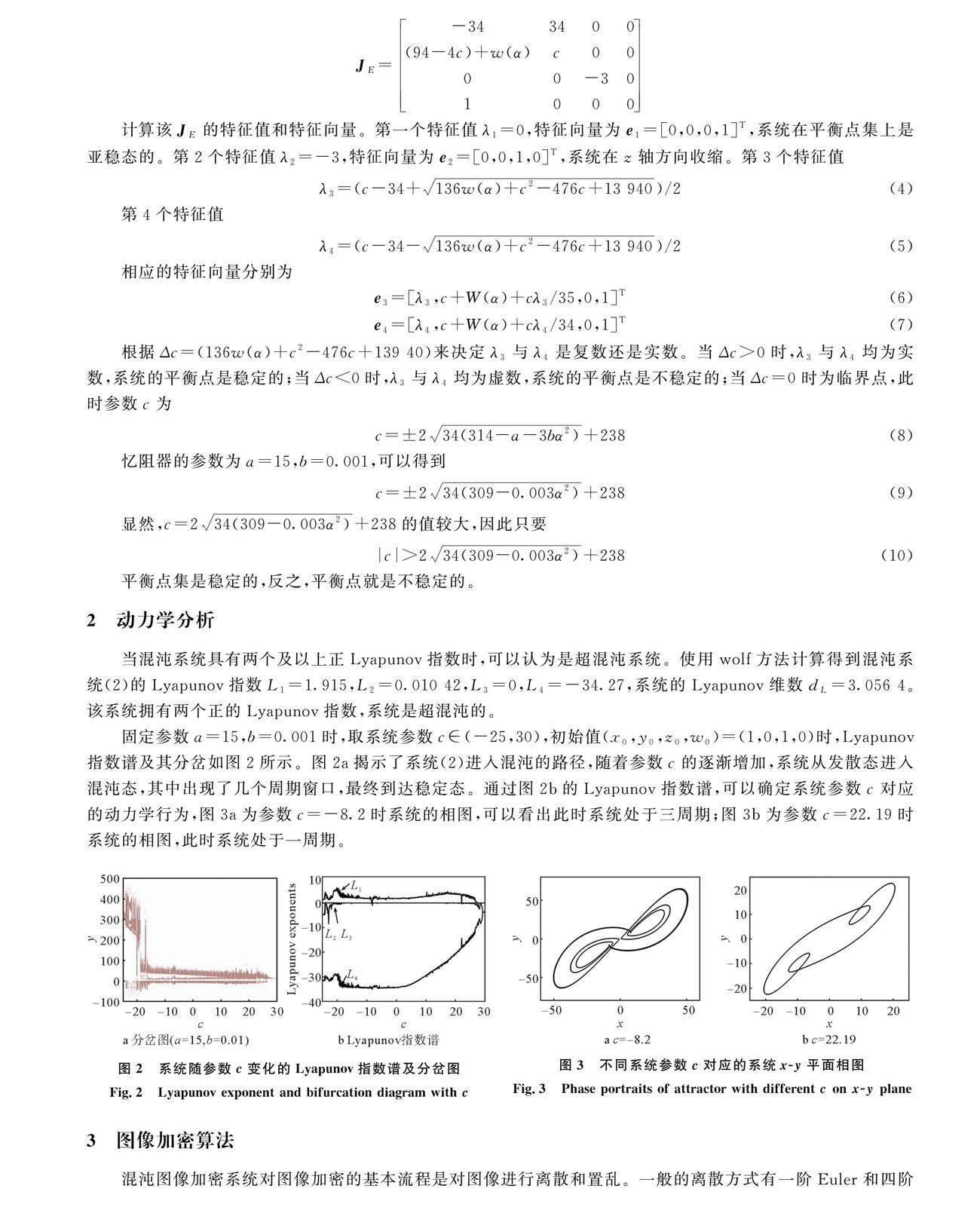
本文通过引用光滑三次型忆阻器构建了一个改进的四维超混沌系统，并对系统的相图、Lyapunov指数和分岔等动力学进行分析，结果表明该系统具有超混沌特性。然后将此超混沌系统应用在新型图像加密系统上，加密前通过哈希算法产生混沌系统的初始值、迭代次数和置乱倍数，在混沌发生器产生伪随机序列后进行序列的选择。最后采用选取的混沌序列进行置乱-对角翻转-扩散-循环移位-上下翻转操作得到加密图像。最后，通过直方图分析、信息熵分析、鲁棒性分析等验证，表明该图像加密算法具有密钥空间较大，加密后相关性较小、抗干扰能力强、信息熵接近理论值，加密性能好等特点，可广泛应用于图像加密领域。

参考文献：

［1］CHUA L O. Memristor the missing circuit element ［J］. IEEE Trans Circuit Theory，1971，18（5）：507-519.

［2］CHUA L O， KANG S M. Memristive devices and systems［J］. Proc IEEE， 1976， 64（2）：209-223.

［3］ZHANG Y， WANG X， FRIEDMAN E G. Memristor-based circuit design for multilayer neural networks［J］. IEEE Transactions on Circuits and Systems Part 1 Regular Papers， 2018， 65（2）：677-686.

［4］GAO C， LI T， CAO X， et al. Identification circuit based on memristor［J］. Journal of Physics Conference Series， 2021， 1827（1）：012007.

［5］SHCHANIKOV S， ZUEV A， BORDANOV I， et al. Design and simulation of memristor-based artificial neural network for bidirectional adaptive neural interface［DB/OL］.［2021-06-01］.  https：//arxiv.org/abs/2004.00154.

［6］LUO L， HU X， DUAN S， et al. Multiple memristor series-parallel connections with use in synaptic circuit design［J］. Iet Circuits Devices & Systems， 2017， 11（2）：123-134.

［7］MATTHEWS R. On the derivation of a "Chaotic" encrypt- ion algorithm［J］. Cryptologia， 1989， 13（1）：29-41.

［8］YANG S. Dynamical analysis and image encryption application of a novel memristive hyperchaotic system［J］. Optics & Laser Technology， 2021， 133（1）：106553.

［9］汪彥， 涂立. 基于改进Lorenz混沌系统的图像加密新算法［J］. 中南大学学报（自然科学版），2017，48（10）： 2678-2685.

WANG Y， TU L. A new image encryption algorithm based on improved Lorenz chaotic system［J］. Journal of Central South University （Science and Technology）， 2017， 48（10）： 2678- 2685.

［10］ 谢国波， 姜先值. 二维离散分数阶Fourier变换的双混沌图像加密算法［J］. 计算机工程与应用，2018， 54（3）：40-45.

XIE G B， JIANG X Z. Double chaotic image encryption algorithm based on two dimensional discrete fractional fourier transform［J］. Computer Engineering and Applications， 2018， 54（3）：40-45.

［11］ 朱淑芹， 李俊青. 一种混沌图像加密算法的选择明文攻击和改进［J］. 计算机工程与应用，2017，53（24）：113-121.

ZHU S Q， LI G Q. Chosen plain text attack and improvements of chaos image encryption algorithm［J］. Computer Engineering and Applications， 2017， 53（24）： 113-121.

［12］ 付正， 李嵘. 基于新型切换Lorenz混沌系统的图像加密算法研究［J］. 计算机与数字工程，2020， 48（1）：170-173.

FU Z， LI R. Application of a switched lorenz chaotic system in image encryption［J］. Computer & Digital Engineering， 2020， 48 （1）：170-173.

［13］ 张永红， 张博. 基于Logistic混沌系统的图像加密算法研究［J］. 计算机应用研究，2015， 32（6）：1770-1773.

ZHANG Y H， ZHANG B. Algorithm of image encrypting based on Logistic chaotic system［J］. Application Research of Computers， 2015， 32 （6）： 1770 -1773.

［14］ 王静， 蒋国平. 一种超混沌图像加密算法的安全性分析及其改进［J］. 物理学报，2011，66（6）：89-99.

WANG J， JIANG G P. Cryptanalysis of a hyper-chaotic image encryption algorithm and its improved version［J］. Acta Phys Sin，2011，66（6）：89-99.

［15］ 李偉岸， 熊祥光， 夏道勋. 基于超混沌和Slant变换的鲁棒水印算法［J］. 计算机工程与科学，2020， 42（5）：55-61.

LI W A， XIONG X G， XIA D X. A robust watermarking algorithm based on hyper-chaotic and Slant transform［J］. Computer Engineering & Science，2020，42（5）：55-61.

［16］ 程东升， 谭旭， 许志良，等. 结合四维超混沌系统和位分解的图像加密算法研究［J］. 电子科技大学学报， 2018， 47（6）：108-114.

CHENG D S， TAN X， XU Z L， et al. Image encryption algorithm research by combining four dimensional hyper-chaotic system and bit decomposition ［J］. Journal of University of Electionic Science and Technology of China， 2018， 47（6）：108-114.

［17］ 阮静雅， 孙克辉， 牟俊. 基于忆阻器反馈的Lorenz超混沌系统及其电路实现［J］. 物理学报， 2016， 65（19）： 190502.

RUAN J Y， SUN K H， MOU J. Memeristor-based Lorenz hyper-chaotic system and its circuit implementation ［J］. Acta Phys Sin， 2016，65（19）： 190502.

［18］ 蔡国梁， 黄娟娟. 超混沌Chen系统和超混沌Rossler系统的异结构同步［J］.物理学报，2006， 55（8）：3997-4004.

CAI G L， HUANG J J. Synchronization for hyperchaotic Chen system and hyperchaotic Rossler system with different structure ［J］. Acta Phys Sin， 2006， 55（8）：3997-4004.

［19］ YONG Z. The unified image encryption algorithm based on chaos and cubic S-Box［J］. Information Sciences， 2018， 450：361-377.

［20］ ALGREDO B I， FEREGRINO U C， CUMPLIDO R， et al. FPGA-based implementation alternatives for the inner loop of the secure hash algorithm SHA-256［J］. Microprocessors & Microsystems， 2013， 37（6/7）：750-757.

［21］ SHAKIBA A randomized CPA-secure asymmetric color image encryption scheme based on the Chebyshev mappings and one-time pad ［J］. Journal of King Saud University-Computer and Information Sciences， 2021， 33（5）：562-571.

［22］ CHAI X L， FU X L， GAN Z H， et al. A color image cryptosystem based on dynamic DNA encryption and chaos［J］. Signal Processing， 2019， 155：44-62.

（责任编辑 耿金花）