双噪声激励下的基因转录调控系统的稳态分析

张萌 郭永峰 刘倩茹

摘要：

鉴于噪声对生物系统的基因转录调控有着重要的影响作用，研究了乘性高斯白噪声和加性Lévy噪声共同激励下的基因转录调控系统的动力学特性。首先借助Janicki-Weron算法模拟出Lévy噪声，然后利用四阶Runge-Kutta 算法计算出蛋白质浓度的稳态概率密度函数，并通过绘制其图像对系统的动力学行为进行稳态分析。研究发现：高斯噪声强度、Lévy噪声强度、稳定性指标、偏斜参数均会诱导蛋白质浓度发生相变现象，且这些参数指标的增大会使基因转录调控系统逐渐从“开启”状态转变为“关闭”状态。

关键词：

基因转录调控系统；Lévy噪声；高斯白噪声；稳态概率密度；相变

中图分类号： O414.2；O415.6     文献标识码：A

收稿日期：2021-09-17；修回日期：2022-04-26

基金项目：

国家自然科学基金（11672207）；天津市自然科学基金（17JCYBJC15700）

第一作者：

张萌（1997-），女，天津人，硕士研究生，主要研究方向为应用概率统计。

通信作者：

郭永峰（1980-），男，山东济宁人，博士，教授，主要研究方向为随机动力系统，应用概率统计等。

Steady-state Analysis of the Gene Transcriptional Regulation System Under the Double-noise Excitation

ZHANG Meng， GUO Yongfeng， LIU Qianru

（School of Mathematical Sciences， Tiangong University， Tianjin 300387， China）

Abstract：

Noise is playing an important role in the regulation of gene transcription in biological systems. This paper studies the dynamics of gene transcription regulation system under the effects of multiplicative Gaussian white noise and additive Lévy noise. Firstly， the Lévy noise is simulated with the Janicki-Weron algorithm， and then the fourth-order Runge-Kutta algorithm is used to calculate the steady-state probability density（SPD） function of the protein concentration， then the steady state analysis of the gene transcriptional regulation system is carried out by the SPD figures. The study found that Gaussian noise intensity， Lévy noise intensity， stability index， and skewness parameter all can induce phase transitions in the gene transcription regulation system; At the same time， the increase of these parameters will cause the gene transcription regulation system to gradually the " on" state changes to the "off" state.

Key words：

gene transcriptional regulation system; Lévy noise; Gaussian white noise ; steady-state probability density; phase transitions

0 引言

近些年，由噪声引起的跃迁、非平衡相变、随机共振等现象被一些学者广泛关注［15］。噪声驱动的动力系统的研究已涉及到物理、化学、经济、生物等多个学科领域。例如，文献［6］和［7］研究了不同类型噪声激励下Duffing系统的随机分叉和随机共振现象；文献［8］探讨了双稳系统中周期信号在大参数频率范围内的随机共振现象。文献［9］提出了二次采样的随机共振技术，实现了绝热近似理论在大參数条件下从强噪声中提取弱信号的目标。另外，在生物系统的基因转录调控方面，已有的实验研究表明，噪声扰动常常发生在基因表达的转录、降解、翻译和结合等不同阶段［1013］，并且噪声在基因转录的过程中可以诱导蛋白质浓度发生“双开关”现象［14］。因此，研究随机噪声激励的基因转录调控系统的动力学特性具有非常重要的实际意义。

基因转录调控系统是生物学交叉研究的核心问题，也是基因工程理论与实践的基础。目前，基因转录调控系统受到了许多专家学者持续广泛的关注，并对此进行了深入的研究。文献［15］基于Smolen等提出的基因转录调控系统动力学模型，从理论与数值两方面研究了降解反应速率和合成反应速率波动对转录因子的影响；文献［16］研究发现噪声不相关时基因开关切换过程仅与降解反应速率有关，而噪声相关时遗传调控系统中噪声间的互相关强度和合成反应速率亦会影响基因开关的切换。以往的研究多集中在高斯白噪声诱导的基因转录调控系统，但是高斯白噪声只是一种理想的状态，不能精确地模拟实际情况。现有的一些对于生物动力系统的研究表明，基因转录调控过程中的随机扰动会以一种突发性的、跳跃性的、不可预测性的方式发生，这些特性可以用非高斯Lévy噪声进行模拟［1718］。由此可见，非高斯噪声对基因转录调控等动力学系统的影响是不可忽略的。如文献［19］考虑了加性非高斯Lévy噪声对基因调控系统稳态概率密度和平均首次穿越时间的作用机制。文献［20］研究了非高斯噪声驱动的基因转录调控系统中噪声的各个参数对随机引力盆的影响。文献［21］分析了噬菌体基因调控中乘性非高斯噪声对系统稳态概率密度和平均首次穿越时间的影响。文献［22］通过蒙特卡洛方法对Lévy噪声进行模拟，探讨了Duffing-van der Pol系统的随机分岔现象。文献［23］分析了不同类型噪声作用下耦合神经网络中脉冲信号的传输机制。文献［24］研究了非高斯噪声激励下含周期信号 FitzHugh-Nagumo神经元系统的响应特征。但对于高斯白噪声和Lévy噪声共同激励的基因转录调控系统的研究还尚未见到。

本文主要针对乘性高斯白噪声和加性Lévy噪声共同激励的基因转录调控系统的稳态动力学特性进行研究。利用Janicki-Weron算法产生Lévy噪声，并通过四阶Runge-Kutta算法模拟出方程的稳态概率密度函数；进一步分析了高斯白噪声和Lévy噪声对系统稳态概率密度的影响以及基因转录系统在“开启”状态和“关闭”状态之间的相互转换关系。

3 基因转录调控系统的稳态分析

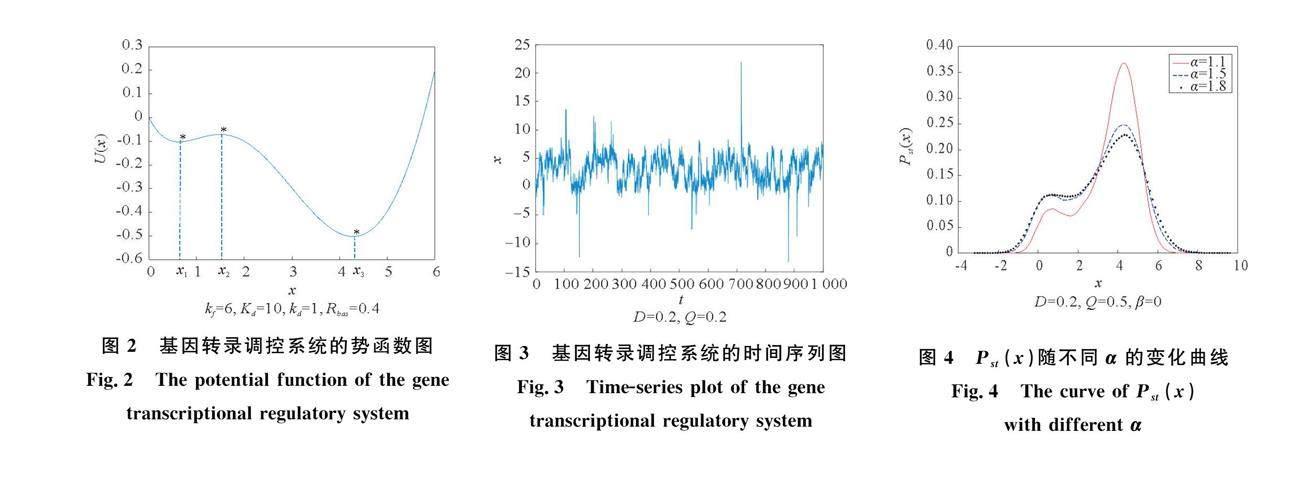
根据上述数值模拟方法，图4～图7分别给出了稳态概率密度函数pst（x）随稳定性指标α、偏斜参数β、Lévy噪声强度Q、高斯噪声强度D的变化曲线。

由文献［19］和［20］可知，Lévy噪声的稳定性指标α∈（1，2）时为非高斯分布，当α=2时，Lévy噪声转变为高斯白噪声。图4给出了Lévy噪声为非高斯情形时稳态概率密度函数的变化曲线，从图4可以看出，随着Lévy噪声的稳定性指标α的增大，稳态概率密度函数曲线左峰逐渐升高，右峰逐渐降低，基因转录调控系统的稳态概率密度函数逐渐由单峰状态转变为双峰状态，蛋白质浓度从高浓度状态向低浓度状态转移，发生了相变现象。这表明Lévy噪声的稳定性指标α可以诱导基因开关发生转变。

图5 为不同Lévy噪声的偏斜参数β对稳态概率密度影响的变化曲线，当β<0时，稳态概率密度函数曲线右边的峰较高，蛋白质浓度主要集中在高浓度区域，基因处于开启状态。但随着β的增大，稳态概率密度峰值向左移动，且从单峰变为双峰结构，表明蛋白质浓度逐渐由高浓度转向低浓度状态。当β>0时，左边的峰值不断升高，曲线又从双峰结构变为单峰结构。此时，蛋白质浓度主要集中在低浓度区域，基因处于“关闭”状态。由此可见，偏斜参数β的变化也可以控制基因的开关。

图6 给出了不同Lévy噪声强度Q对稳态概率密度的影响变化曲线。当Lévy噪声强度Q较小时，蛋白质浓度主要集中在高浓度区域，基因处于“开启”状态，但随着噪声强度Q的增大，左峰逐渐升高，右峰逐渐降低，蛋白质浓度逐渐从高浓度区域向低浓度区域转移，由此可见，Lévy噪声强度Q可以诱导基因转录的开关。

图7 为不同高斯噪声强度D对概率密度的影响变化曲线，从图7可以看出，当高斯噪声强度D较小时，蛋白质浓度主要集中在高浓度区域，此时基因处于开启状态，随着高斯噪声强度D的增大，左峰明显升高，右峰明显降低，蛋白质浓度从高浓度向低浓度转移，基因逐渐向“关闭”状态转变，这说明高斯噪声强度D亦能够诱导基因开关的转换。

4 结论

本文主要分析了加性高斯白噪声与乘性Lévy噪声共同作用下的基因转录调控系统的复杂动力学特性。首先利用Janicki-Weron算法产生Lévy噪声，然后利用四阶Runge-Kutta算法模拟基因转录调控系统的蛋白质浓度的稳态概率密度函数，通过模拟出的稳态概率密度函数图像分析了高斯白噪声与Lévy噪声共同作用下蛋白质浓度大小的转变关系。研究发现：稳定性指标α、位置参数指标β、乘性Lévy噪声强度Q、加性高斯白噪声强度D均可以诱导基因开关的转换，并诱导蛋白质浓度由高浓度向低浓度转移。

参考文献：

［1］胡岗. 随机力與非线性系统［M］. 上海：上海科技教育出版社， 1994：125-183.

［2］KRAMERS H A. Brownian motion in a field of force and the diffusion model of chemical reactions［J］. Physica， 1940， 7（4）：284-304.

［3］GHOSH P K ， BARIK D ， RAY D S. Noise-induced transition in a quantum system［J］. Physics Letters A， 2005， 342（1/2）：12-21.

［4］MANGIONI S E， DEZA R R， et al. Nonequilibrium phase transitions induced by multiplicative noise： effects of self-correlation［J］. Phys Rev E， 2000， 61（1）：223-232.

［5］BIERWIRTH M ， Using single transients on the performance analysis of electrochemical noise amplifiers［J］. Materials and Corrosion， 2013， 64：664-670.

［6］XU Y， GU R C， ZHANG H Q， et al. Stochastic bifurcations in a bistable duffing-van der pol oscillator with colored noise［J］. Physical Review E， 2011， 83（5）：056215.

［7］李娟娟， 许勇， 冯晶. Duffing系统中Lévy噪声诱导的随机共振与相转移［J］. 动力学与控制学报， 2012， 10（3）：278-282.

LI JJ ， XU Y ， F J. Stochastic resonance and phase transfer induced by lévy noise in duffing system［J］. Journal of dynamics and control， 2012， 10（3）：278-282.

［8］杨定新，胡政，杨拥民.大参数周期信号随机共振解析［J］.物理学报，2012， 61（8）：50-59.

YANG DX ， HU Z ， YANG Y M. Stochastic resonance analysis of large parameter periodic signals［J］. Acta Physica Sinica， 2012， 61（8）：50-59.

［9］冷永刚，王太勇， 二次采样用于随机共振从强噪声中提取弱信号的数值研究［J］. 物理学报， 2003， 52（10）：2432-2437.

LENG YG ， WANG T Y. Numberical research of twice sampling storchastic resonance for the detection of a week signal submerged in a heavy noise［J］. Acta Physica Sinica， 2003， 52（10）：2432-2437.

［10］ XIE Q S， WANG T H， ZENG C H， et al. Predicting fluctuations-caused regime shifts in a time delayed dynamics of an invading species［J］. Physica A： Statistical Mechanics and Its Applications， 2018， 493：69-83.

［11］ SMOLEN P ， ET A L. Frequency selectivity， multistability， and oscillations emerge from models of genetic regulatory systems.［J］. American Journal of Physiology. Cell Physiology， 1998， 274（2）：C531-C542.

［12］ RAJ A ， OUDENAARDEN A V. Nature， nurture， or chance： stochastic gene expression and its consequences［J］. Cell， 2008， 135（2）：216-226.

［13］ LI G W， XIE X S. Central dogma at the single-molecule level in living cells.［J］. Nature， 2011， 475： 308-315.

［14］ 刘泉. 基因转录调节动力学中的随机性质：涨落诱导基因开关［D］. 武汉：华中师范大学， 2004.

LIU Q. Random properties in the dynamics of gene transcriptional regulation： fluctuation induced gene switching［D］. WUHAN： Central China Normal University， 2004.

［15］ SMOLEN P， BAXTER D A， BYRNE J H. Mathematical modeling of gene networks［J］. Neuron， 2000， 26（3）：567-580.

［16］ LIU Q ， JIA Y. Fluctuations-induced switch in the gene transcriptional regulatory system［J］. Physical Review E， 2004， 70（4）：041907.

［17］ GOLDING I， PAULSSON J，  ZAWIISKI S， et al. Real-time kinetics of gene activity in individual bacteria［J］. Cell， 2005， 123（6）：1025-1036.

［18］ RAJ A， PESKIN C S， TRANCHINA D， et al. Stochastic mRNA synthesis in mammalian cells［J］. Plos Biology， 2006， 4（10）：e309.

［19］ XU Y， FENG J， LI J J， et al. Lévy noise induced switch in the gene transcriptional regulatory system［J］. Chaos， 2013， 23（1）： 013110.

［20］ SONG Y， XU W. Stability of a gene transcriptional regulatory system under non-gaussian noise［J］. Chaos， Solitons & Fractals， 2020， 130： 109430.

［21］ CHEN X， KANG Y M， FU Y X. Switches in a Genetic regulatory system under multiplicative non-gaussian noise［J］. Journal of Theoretical Biology， 2017， 435： 134-144.

［22］ 顧仁财，许勇，郝孟丽，等. Lévy稳定噪声激励下的Duffing-van der Pol振子的随机分岔［J］. 物理学报， 2011， 60（6）：157-161.

GU CR ， XU Y ， HAO M L， et al. Stochastic bifurcations in duffing-van der Pol oscillator with lévy stable noise［J］. Acta Physica Sinica， 2011， 60（6）：157-161.

［23］ 方鸿雁，潘园园，孙华通，等.耦合神经网络中脉冲信号传输的噪声增强研究［J］.复杂系统与复杂性科学，2017， 14（2）：59-64.

FANG HY ， PAN Y Y ， SUN H T， et al. Study of noise-enhanced pulse signal transmission in coupling neural networks［J］. Complex Systems and Complexity Science， 2017， 14（2）：59-64.

［24］ 徐超，康艳梅.非高斯噪声激励下含周期信号FitzHugh-Nagumo系统的响应特征［J］.物理学报，2011，60（10）：742-749.

XU C， KANG YM. Mean response time of FitzHugh-Nagumo model in the presence of non-gaussian noise and a periodic signal［J］. Acta Physica Sinica ， 2011， 60（10）：742-749.

［25］ WERON A ， WERON R. Computer Simulation of Lévy α-stable Variables and Processes［M］. Berlin Heidelberg： Springer， 1995： 379–392.

［26］ WERON R. On the chambers-mallows-stuck method for simulating skewed stable random variables［J］. Stat Probabil Lett 1996， 28（2）：165–71.

［27］ GUARCELLO C ， FILATRELLA G ， SPAGNOLO B ， et al. Voltage drop across Josephson junctions for Lévy noise detection［J］. Physical Review Research， 2020， 2（4）： 043332.

［28］ REBECCA L H. Stochastic runge-kutta algorithms. I. white noise［J］. Physical Review A， 1992， 45（2）： 600-603.

（責任编辑 李 进）